Алгоритмы решения задачи идентификации
Автор: Плотникова Наталья Валерьевна, Калистратова Наталья Сергеевна, Малявкин Олег Николаевич
Статья в выпуске: 14 (69), 2006 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/147154566
IDR: 147154566
Текст статьи Алгоритмы решения задачи идентификации
В последнее время в связи с предъявлением все более высоких требований к процессам управления в различных областях техники проблема идентификации становится исключительно важной.
Выбор метода идентификации определяется конкретной задачей, техническими возможностями (условия проведения эксперимента, возможности обработки на ЭВМ и т.п.). Одним из современных вычислительных методов является метод сплайн-интерполяции и аппроксимации.
1. Алгоритм решения задачи с использованием весовой функции
Пусть имеется линейная стационарная непрерывная система автоматического управления, имеющая один входной и один выходной сигнал.
Динамические свойства описываемой системы могут быть определены по ее функции веса [1]. Для входного воздействия произвольного типа, прикладываемого в момент времени t = 0, переходный процесс на выходе звена при нулевых начальных условиях может быть определен на основании интеграла свертки t t
y(z) = |x(t)©(z-t)(1) о о
Пусть известны дискретные значения входного сигнала через равноотстоящие интервалы времени на интервале Z е [0, Z^, тогда, аппроксимируем функцию на входе системы сплайном нечетного порядка [2].
nOi + «1 it + агх? + азх? +... + ам xtM,
- J а02 + a12Z + а22^2 + W3 + • ■ • + аМ2^ > a0N + alNt + a2Nt2 + Пз,у^3 + ■ • • + aMNtM , где ау - коэффициенты сплайна входного сигнала.
Аналогично аппроксимируем весовую функцию сплайном того же порядка, что и у сплайна входного сигнала (2)
®(0 = ■
vOi + vnZ + v21Z2 + v31Z3 -V... + vMxtM, V02 + V12f + V22^ + V32^ + • • ■ + vM2tM
^ON + ^IN1 + v2Nt + VW + • • ■ + V^t , где v,2 - коэффициенты сплайна весовой функции. ■ Для определения выходного сигнала воспользуемся интегралом свертки (1). Рассмотрим подробнее подынтегральную функцию, состоящую из произведения двух функций. Она является функцией двух переменных t и т, может быть записана как:
П(/,т) = ©(т)х(г-т). (4)
Так как сплайн является кусочно-представимой функцией, то и подынтегральная функция П (Z,t) будет кусочно-представимой (рис. 1).
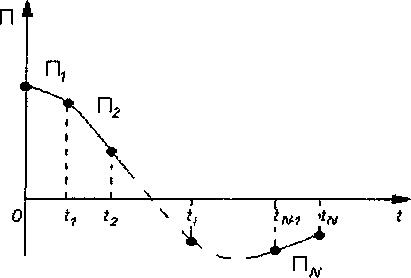
Рис. 1. Кусочно-представимая подынтегральная функция
Определение выходного сигнала из интеграла свертки (1) сразу в виде функции нецелесообразно, так как в результате произведения двух сплайнов и их интегрирования будет получаться полином высокого порядка (2М+ 1), где М- порядок сплайна. Поэтому будем искать выходной сигнал в виде дискретных значений через равноотстоящие интервалы времени.
Для определения значения выходного сигнала в момент времени t^ необходимо найти интеграл свертки для фиксированного интервала времени
АЧ^ = /о)(т)х(?4-т)с?т. (5)
о
Интеграл (5) можно представить в виде суммы интегралов:
|©(t)x(z4-t) 0о <2Д + J©(x)x(zi-т)^т + ...+ J ©(t)x(z4-т)т(6) <1Д-1 или Д J©(t)x(Z4 -т)(/т = jn^Z^jT^T-t- 0о <2Д + ]п2^,т>/т + ...+ jnt(tt,T)dT.(7) АД-1 Так как сплайн определяется на каждом интервале разбиения отдельным полиномом, то для вычисления каждого из суммируемых интегралов (6) необходимо определить, какие полиномы сплайнов входного сигнала и весовой функции участвуют в формировании каждой подынтеграль- ной функции. Рассмотрим один из интегралов, входящих в сумму: J ^(т)^^-vylT = j П,-(z^jT^t . (8) 9-1 ^-' Для нахождения интеграла (8) при переходе к конкретным полиномам, вместо весовой функции ю(?) необходимо подставить полином о/О, определенный на интервале [z,_btj\, вместо функции входного сигнала подставляется полином x^z), определенный на интервале [?*-{,, tk- W], так как функция смещается, благодаря разности аргумента tk-t. Таким образом, значение подынтегральной функции П(/,т) в любой точке интервала [^ь Гу] может быть определено по формуле: П,^,т) = оу(т)хА_>+1(/4-т).(9) При переходе к полиномам, выражение (9) примет вид: м м , п; (= X (v') Е ai,k-A (ч - ТУ ■ (1 °) 1=0i=0 По формуле (10) находим значения функции П(4,т) в каждом узле рассматриваемого интервала: ' м ( -\М IЛ Чок 1=0/=0 М / М /А i=0i=0' м ,м , ' Ч1к =E(V'2?2)E(aU-l(^ ”^2) В (11) |=оi=0 М м ,.. Чкк = ^\vik4y^Aail(tk ~Ч^ i=0 i=0V' Имея известные значения qir функции П^,т), где j - номер текущего узла, г - номер конечного узла равномерной сетки, в соответствующих узлах tj, можно найти значение выходного сигнала в момент времени tk. Для этого по найденным значениям (11) строится сплайн F^f) /01 +/u?+/2if2 +/з1;3км/4; F(z) = < ^2 +/12Z +/22^ + Лз^ + • • Q2) .fok + f\kt + flk^ + // + ■ • ■ + fMktM • Таким образом, задача определения значения выходного сигнала в момент времени tk, согласно (5), сводится к нахождению определенного интеграла (площади под кривой F(z) (рис. 2): )W-№dt- (13) о Интеграл (13) будем рассчитывать как сумму интегралов от отдельных полиномов: Jf(z)^ = о О z2 = |д oyt+ Jf20У< + --- + j Fk(t)dt.(14) 0 'i Полином Fy(/) имеет вид: Fj(O = fOj+fAjt + V+... + fMjtM, (15) где /у - коэффициенты сплайна. Найдем интеграл от полинома F^f) Sj- Wo- Рис. 2. Сплайн-аппроксимация подынтегральной функции П(4,т) Выражение (16) можно также записать в виде: Подставляя пределы интегрирования, получим: Й г + 1 * + 1 Поставляя полученное выражение (18) в (13), с учетом (14), получим формулу для определения выходного сигнала в момент времени tk Остальные значения выходного сигнала y(tj) находятся аналогично описанному выше алгоритму. Значение выходного сигнала в начальный (нулевой) момент времени, согласно принципу физической реализации системы (система не может мгновенно преобразовать входное воздействие), равно нулю. С учетом выше сказанного, получим массив точек выходного сигнала у е (0, уь ...,ум) на равномерной сетке t е (0, tb ..., tNy В заключении, по найденным значениям у строится сплайн y(t) boN + Ьщ* + Ь^цГ + b3Nt +... + b^t . где 6,, - коэффициенты сплайна выходного сигнала. Пусть известны дискретные значения входного и выходного сигналов через равноотстоящие интервалы времени на интервале / е [О, ГЛ], тогда, аппроксимируем функции на входе и выходе системы сплайнами нечетного порядка (выражения (2) и (20), соответственно). Необходимо найти весовую функцию системы в виде (3). Непосредственно из интеграла свертки (1) выразить весовую функцию невозможно. Поэтому, рассмотрим совокупность значений подынтегральной функции П(^,т) в узлах /,(11) чок = E(vii0')E ); 1=01=0 м м,., , |=о 1=0v' М м ,., 92k= Е (VZ2^2 ) Е ( ЯМ-1 Ot ~ ^2 ) Р 1=0 i=0х' м м ... Чкк= Е(У»4)Е(ЯМ (^ ~^) г . 1=01=о Можно заметить, что в правых частях выражений первые множители представляют собой значения весовой функции в соответствующих узлах tj. Вторые множители, после подстановки конкретных значений, представляют собой некоторые коэффициенты ujk. С учетом выше сказанного выражение (11) примет вид: Ч»к = ®QuOk’ qxk =toxuxk, qlk =®ги1к' Чкк - ®кикк’ где to, - значения весовой функции в соответствующих узлах равномерной сетки гу. В системе уравнений (21) неизвестными считаем искомые значения весовой функции соу и значения подынтегральной функции qjk. Таким образом, система имеет 2(6 + 1) неизвестных и (6+1) уравнений. Коэффициенты и)к известны, так как для их расчета требуется знать только сплайн входного сигнала. Система уравнений (11), а значит и система (21), составлена для расчета выходного сигнала только в момент времени tk. Если составить аналогичные системы для каждого узла равномерной сетки, кроме нулевого, то получим N систем уравнений вида (22). 9о2= ю0м02 [9oi “ ®омор 912= ^“ы; 1911 =<¥п; 922 = Ю2М22 9ол-1 ~ ®омол-1; 9on= ^o^oiV’ 91 Л-1 - ю1м1 л-1 9л = ю1м1дг; 9гл-1 = ®2^2Л-1 42N = ®2U2N’ _9дмл-1 = ®w-iu N-1 Л-1 ’ ^NN = ®NUNN Число неизвестных уменьшилось по отношению к числу уравнений, так как в каждой системе присутствуют повторяющиеся значения весовой ФУНКЦИИ (0у. Полученные системы уравнений (22) несут известную информацию только о входном сигнале системы (коэффициенты и,,). Для получения недостающих уравнений, определим связь полученных систем с выходным сигналом. Располагая значе ниями qJr можно рассчитать площади под кривыми, и тем самым найти значения выходного сигнала в соответствующих узлах 1Г Если искать площадь под кривой с использованием сплайнов, то появятся избыточные условия, что не даст возможности найти значения весовой функции. Поэтому для определения площади будем использовать метод трапеций, так как он наиболее приемлемый и при разбиении мелкой сеткой достаточно точный. Согласно методу трапеций значение интеграла на каждом участке разбиения определяется как площадь трапеции по формуле: где h - шаг сетки сплайна. Значение выходного сигнала в момент времени tk, запишется в виде: ^(ч) ” л+-^2+---+4=Е^ • ^4) 1=1 С учетом (23) выражение (24) имеет вид: И^) “^[2?0Л +9u +92t +--- + ft-u +2fe] • (25) Если составить аналогичные выражения для каждого узла равномерной сетки, кроме нулевого, то получим систему N уравнений: "V^N + 9л +..- + 9^-1Л +2?да] -V^nY "^-Qon-a +4i,n-i + • ■ • + 29^!Л-1 ] = j(^-i); .... (26) - [2^02 + 912 + 2^22 З^З'Ог); |[2%1 + 29и] = У М- Подставим в полученную систему уравнений (26) значения qJk из систем уравнений (19), в результате получим систему (27). Полученная система N уравнений имеет (А+ 1) неизвестных со;. Получим недостающее уравнение. Для этого найдем производную от интеграла (1). Согласно теореме Барроу, производная от интеграла с переменным верхним пределом, по верхнему пределу, равна подынтегральной функции, где вместо переменной интегрирования стоит переменный верхний предел. г - |_2соомОЛ, + mxuXN +... + toN_xuN_XN + +2о)Л,иУЛ,]-^ —[2о0ио,1У-1+ С01м1,лг-1 + • • • + 2tt>w_i х ' xм^-l,^-l ]=у ^n-i ); (27) h - [2ю0м02 + c)^ + 2й2м22 ] = у (z2) ^ ю0м01 + 2o1K11] = y(z1). dy^ dt Выразим из (28) значение весовой функции: ®(°) = 4т- (29) Значению весовой функции в нулевой момент времени соответствуют значения входного сигнала и производной выходного сигнала в нулевой момент времени: <30) При подстановке в выражение (30) сплайна входного сигнала и производной сплайна выходного сигнала соответственно получим отношение только двух коэффициентов сплайнов, так как остальные обнулятся: = (31) “01 где а0] и fen - коэффициенты сплайнов (2) и (20). Полученное уравнение (31) подставим, как недостающее в систему уравнений (27), и раскроем скобки: htt>0u0N + 0, Sh®xuXN +... + 0,5hmN_xuN_XN + +htoNum = у^мУ, йю0и0Л,_1 + 0,5h(BxuX N_x +... + htoN_x x * xun-yn-i =tOzv-i); (32) ha0u02 + O,5hoxux2 + h(o2u22 = у^2\, h(d0uQX+hoxuxx =y(?]), ГДе O0 = feH/ Система уравнений (32) решается методом обратного хода, в результате чего определяются значения весовой функции во всех узловых точках. Затем строится сплайн весовой функции. 2. Алгоритм решения задачи с использованием коэффициентов передаточной функции Пусть известны дискретные значения входно го сигнала через равноотстоящие интервалы вре мени на интервале t е [0, z^]: “01 + “1 \t + Я2Т~ +«з/ ■ ■ • *(0 = Я02 + “12^ + а22^2 + Я32;3 ■ • ‘ аМ2{М 5 a0N +aXNt + a2Nt + a3Nt ■ ■■+MNt , где ay - коэффициенты сплайна входного сигнала. Аппроксимируем функцию на входе системы сплайном нечетного порядка. Выберем нечетный порядок сплайна [2], так как он более точно аппроксимирует заданную функцию, по сравнению со сплайном четного порядка. Для простоты будем рассматривать сплайн только на Ам интервале, полагая, что на остальных интервалах коэффициенты выходного сплайна находятся аналогичным образом: х^^а^, (34) 4=0 где ад - коэффициенты входного сплайна на Ам интервале. Также известны коэффициенты числителя и знаменателя передаточной функции, которая в общем случае имеет вид: da+dxp+d2p2+...+dnp'1 Выходной сигнал системы также может быть представлен в виде сплайна того же порядка, что и входной сигнал (33). На Ам интервале выходной сплайн будет иметь вид: т У^ = ^Ь^, (36) 4=о где Ьд - коэффициенты выходного сплайна на Ам интервале. Для дальнейших рассуждений нам понадобятся производные входных и выходных сплайнов. Раскроем сумму входного и выходного сплайнов, тогда входной сплайн на Ам интервале будет иметь вид: хДг) = = аю +aiXti + ai2tx + ai3tx + alJi + ..Aa^t" . (37) Так как на интервале сплайн представляет собой обыкновенный полином ти-й степени, следовательно, он может быть дифференцирован т раз. Определим все т производных входного сплайна. 22^21 dtw = v-(v-l)-...-2-nZv+ (v + l)v-(v-l)-...-2-aIV+1у + ... ..АпЦт-\у..Лт-н\Х-t^', (38) ^2Mo dtw = m\aim. Выходной сплайн также на z-м интервале будет иметь похожий вид: >№ = ЬЮа-Ьд +bi2t2 +bi3t; + +bi4t* +-+bimt". Данный сплайн также может быть дифференцирован т раз. Определим все т производных входного сплайна. dtw = v-(y-iy — -2-biv + +(у + 1)-у-(у-1)-...-2-6,.„+1^ +... ... + m(m-Yy...-(m-v + Yybim (41) - = m\bim. (42) Определим коэффициенты выходного сплайна, если известны коэффициенты входного сплайна и параметры передаточных функций [1] типовых динамических звеньев. Результаты представлены в таблице. Чтобы найти коэффициенты выходного сплайна, используем формулы (37)-(42). Будем считать, что порядок числителя передаточной функции меньше порядка знаменателя (Z < и) и порядок знаменателя передаточной функции меньше порядка используемого сплайна (и < т). В результате получим: (44) “0 bim-v = (-Г) ' Ут-v+ СГ (™ * v +1)' aim-vti + «О +с2 •(zw-v + 2)-(m-v + l)-tiI.m_v+2 + +4 ■(7M-v + 3)-(»i-v + 2)-(zn-v + l)-a;m_v+3 +... ...+cv •т\т-\у..\т-н\уа(т - -dxym-v + xybim_wX- -d2 \m-v + 2y(m-v + iybim_v+2 - -6?3-(m-v + 3)-(m-v + 2)-(m-v + l)-^_v+3-... ,..-dv-тУт-l)-...-(m-v + l)-bimy, (45) bi0 ="r(co-ai0+ ci-“a + 4>•^'•■Уг +c33\-ai3 +... ... + c„vVa^ +... + С/-l\.aa-dx-bn-d2-2\-bi2 -...-dv-m-(m-Y)-...-(m-v + y)-bimy, (46) Рассмотрим вопросы идентификации системы с использованием сплайн-аппроксимации. Будем считать, что система имеет передаточную функ- Коэффициенты выходного сплайна для типовых динамических звеньев Тип звена Коэффициенты выходного сплайна Усилительное bim — &aim Апериодическое 1-го порядка bim-k = KOim-k -T(m-k + 1)6Z„_M, при k = 0, m; bim+x = 0 Апериодическое 2-го порядка bim-k = КУт-k -T^m-k*X)bim_k+x -T^m-k + 2)(m~k+ l)bim_k+2, при k-0,m; bim+x =0; bim+2 =0 Колебательное 2-го порядка bim-k = Kaim_k -2^T(m-k + V)bim_k+X -T2(m-k + 2\m-k + l)bim_k+2, при k = 0,m; bim+x =0; bim+2 =0 Консервативное bim-k = K^im-k -T2(m-k + 2Xm-k + l)bim_k42, при k = 0,m; ^+1=0; bim+2 =0 Интегрирующее bim-k - K , aim-k-\ > при k - 0, m 1 m-k Дифференцирующее bik =K(k + l)aiM, при k = 0, m -1; bim = 0 Часто передаточная функция системы имеет вид не просто одного типового динамического звена, а различной комбинации типовых динамических звеньев, и передаточную функцию такой системы можно представить в виде отношения полиномов: ’ = (43) uq-vd^p*vd^p -v...-vdnp цию, вид которой известен, т.е. известен порядок числителя и знаменателя передаточной функции, но не известны коэффициенты. Сигналы, подаваемые на исследуемую систему, и получаемые на выходе системы измеряются в некоторые дискретные моменты времени. Таким образом, вход и выход известны и могут быть описаны при помощи сплайнов некоторой степени. Пусть система опи- сывается передаточной функцией вида (35). Пусть математическая модель системы имеет вид: 2 I = (47) d0+dxp + d2p + ... + dnp где у(р) и х(р) - изображения по Лапласу выходного и входного сигналов соответственно. ^)=44’/5и>^=1’ чр) где Жр) - передаточная функция системы. Задача идентификации состоит в определении параметров cb dy передаточной функции W(p) по экспериментально полученному или рассчитанному выходному сигналу системы относительно известного входного. Преобразуем выражение (47): y(p)^d0 + dxp + d2p2 +... + dnp" ) = = (с0+ схр + с2р2 +... + с,р1 )х(р); (48) doyUO + dxpy(p) + d2p2y(p) +... - + dn p"y(p) = cox(p) + cxpx(p) + +c2p2x(p) + ... + clplx(pY (49) Входной и выходной сигналы представляют собой сплайны некоторой степени т, которые можно описать математически следующим образом: N т i=\ j=0 Г- : где N - число точек разбиения сигналов, т - степень сплайна (т > 3), Wy, Vy - коэффициенты разложения в сплайн входного и выходного сигналов соответственно, t-tj^h - шаг разбиения. Таким образом, входной и выходной сплайн на каждом интервале разбиения можно представить так: Xj = wi0+wiXh + wi2 — + ... + win—; ,^ У, = v/o + vzi^ + Чг" + -+%—•( В уравнении (49) р - оператор дифференцирования. Перейдем во временную область: д . л МО , д rf2X0 , , д d"y^ dM0 + dx——+d2 + ... + d„= dt drdt {Ило + dr1X +... + d„_xvin_x + vin ] - -[c0W;0 + c, w,.,+...+ czw/z]} + +^[^0^ +dp-i2+...+ dn4vin + v„,+1]- -[c-oW;! +cxwi2 +...+ CZWZZ+1 ]} + ... - + ;----7t{[^ov™-i + dxvim_I+x +... ... + „_] vZm_z_n+i + vZm_z_„+2]- -[COW™-1 +ClWim-lti + - + ClWim ]} + ... - + —; ^d0Vim-C0Wim^ = 0. Так как полученное выражение равно нулю, то можно предположить, что выражения в фигурных скобках также равны нулю, то есть, получаем систему алгебраических уравнений: 'd0vi0+dxviX + ... + dn_xvin_x + vin = = cowzo+CiWZi+... + c/wi.z; ^ov,i + dxvi2+... + d„_xvin + vin+x = = cowzl+c,wz2+... + czwzz+1; ■ 5 (55) dd^im-l ^~^14m-Z+l "*" — ^"dn_xVXm_i_R+x + +vim-rn+2 = c0wim-l + H^-Z+l +- + clwim"- dovim =cowim. Чтобы система уравнений (55) имела единственное не нулевое решение нужно, чтобы число уравнений системы равнялось числу неизвестных. Число уравнений системы - (т + 1), число неизвестных - (и + / + 1), таким образом, получаем: т+1=п + 1+1=>т = п + 1. Т.е. степень сплайна должна равняться сумме порядков числителя и знаменателя передаточной функции. Пусть для определенности Кп, тогда с учетом последнего равенства перепишем систему алгебраических уравнений (55). doViQ + dxvix +... + d^ +... + dnAvin_x + ^in =c^№ +C1WH +:. + ctvvit; doviX + dxvi2 +... + d^ux +... + dn_xvin + +v;n+i = co wh + C\W- + - + ciwn+i; dx(f) d2x(t) d!x(f) = c0x(p) + C1-^ + c2—^ + ... + c;—^. (54) dt dr dt " Операция дифференцирования применительно к сплайнам вида (52) и (53) осуществляется в соответствии с формулами (37)-(39), (40)-(52). Причем производные порядка (т + 1) и выше равны нулю. Подставим значения для производных в уравнение (54). Перенесем все слагаемые влево и распишем их при одинаковых степенях t. Получим следующее выражение: ‘ dovin +dxvin+x+... + dtvim = (56) = cowin+cxwin+x+... + C!wim; dOvin+x +dxvin+2 +... + di_xvim = = fo^+i + ciwm + - + cmw™ ; dOvim = cowim. Запишем эту систему в матричном виде: ИО = WC , (57) где V - матрица размера (т + 1 )х(и + 1) коэффициентов разложения в сплайн выходного сигнала; D - вектор-столбец (и + 1)х1 коэффициентов знаменателя передаточной функции; W - матрица размера (т + 1)х(/ + 1) коэффициентов разложения в сплайн входного сигнала; С - вектор-столбец (Z + 1)х 1 коэффициентов числителя передаточной функции. V = W = " V0 V] V1 v2 •• v, • •• vz+1 • ■■ v„_ •• v„ 1 v„ " v„+i V/ V/+1 ■" V2Z • •• vm_ 1 vm V/+l V/+2 ■' V2Z+] • " vm 0 v„ v„+i ' •■ vm - 0 0 _Vm 0 ■ .. 0 • •• 0 0 w0 wx ••■ wM wz W] w2 ■■■ wz WZ+1 wz wk\ ••• w2M w2Z Wn Wn+1 ■•■ wm W„+l 4+2 0 . wm 0 ... 0 0 £>-[() J] ... dt dux ... dn_x 1] ; С = [со С1 с2 с/-1 с/] • Запишем (57) в виде: VD-WC-0 (58) Решение уравнения (58) позволяет определить коэффициенты передаточной функции. Выводы 1. Рассмотренный метод построения аппроксимирующего сплайна по экспериментальным данным является достаточно точным, но только при высоком порядке сплайна. Медленная скорость вычислений требует дальнейшей оптимизации алгоритма вычисления. 2. Метод определения выходного сигнала системы, описываемой весовой функцией, обеспечивает достаточную точность при аппроксимации сигналов сплайнами с малыми погрешностями. 3. Определение коэффициентов передаточной функции при использовании сплайн-аппрокси-мации сводится к решению алгебраических уравнений.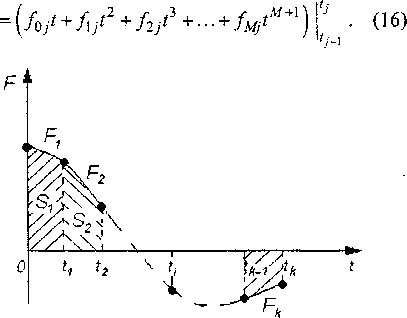

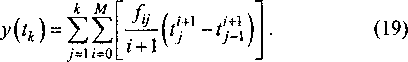
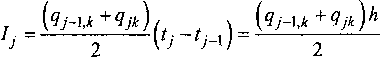
Список литературы Алгоритмы решения задачи идентификации
- Бесекерский В.А., Попов Е.П. Теория систем автоматического регулировании. -М.: Наука, 1975. -768 с.
- Малоземов В.Н., Певный А.Б. Полиномиальные сплайны: Учеб. пособие. -Л.: Изд-во Ленингр. ун-та, 1986. -120 с.


