Алгоритмы совместной обработки разнородной навигационной информации

В последние годы все шире применяется ком-плексирование разнородных наблюдений для определения местоположения движущихся объектов. Например, для морских подвижных объектов (МПО) используются такие навигационные источники, как спутниковые приемники (СРНС), гиперболические радионавигационные системы (РНС), инерциальные системы (ИНС), гидроакустические станции (ГАС), лаги и др.

В литературе описаны различные методы ком-плексирования. В работах [2; 6] рассмотрена условная классификация интегрированных инерциально-спутниковых систем по степени внутренней взаимосвязи.Структурнотакиесистемысостоятиз модуля СРНС, бесплатформенного инерциального измерительного модуля (БИИМ), и совместного модуля, обеспечивающего взаимную интеграцию. От принципа построения последнего модуля как раз и зависит степень интегрированности системы. Условно выделяются слабосвязанная, сильносвязанная и глубокоинтегрированная схемы построения блока совместной обработки навигационной информации. В работе [4] рассмотрен синтез комбинированного оптимального алгоритма комплексирования на первичном и вторичном уровнях. Решение задачи комплексирования представляет собой фильтр на вход которого подаются первичные сигналы. Например, принятые антенной системой СРНС радиосигналы и сигналы с акселерометров и гироскопов ИНС. В результате синтеза получается интегрированная инерциально-спутниковая навигационная система с обработкой всех спутниковых сигналов и измерительных сигналов ИНС в едином блоке (интеграционном фильтре), на выходе которого формируются оценки координат потребителя, его вектора скорости и углов ориентации. Однако реализация таких систем достаточно сложна и не может быть достигну- та на базе существующих приемников СРНС, так как последние имеют традиционную схему построения с двухэтапной обработкой сигналов. Учитывая такую структуру приемников СРНС, были разработаны различные варианты комплексиро-вания на вторичном уровне [2; 5-6], суть которых заключается в том, что измерительные сигналы ИНС и сигналы с выхода блока первичной обработки приемника СРНС (оценки псевдодальностей и радиальных псевдоскоростей) подвергаются совместной комплексной обработке с целью получения более точных оценок координат и вектора скорости потребителя. В [4] рассмотрен метод комплексированияСРНС и ИНС, в котором оценки ускорения или скорости, полученные в комплексном измерителе на вторичном уровне, вводятся в контуры слежения за параметрами спутниковых сигналов, что позволяет сузить их полосы пропускания и повысить помехоустойчивость приемника. Вместе с тем при разработке алгоритмов для современных систем навигации часто приходится сталкиваться с задачами, в которых необходимо учитывать их нелинейный характер [1].

В известных публикация практически отсутс-твуюталгоритмы комплексированиянаблюдений, полученных в различных системах координат. В данной работе рассматриваются возможности оценивания навигационных данных, полученных с помощью ИНС, СРНС и ГАС на основе методов многомерной линейной и нелинейной фильтрации.

Модели источников навигационной информации

Для получения алгоритмов комплексирования информации необходимо построить адекватные модели источников данных. С приёмоиндикато-ра СРНС информация поступает в виде NMEA (National Marine Electronics Association) сообщений, в которых содержатся: географические широта и долгота объекта, скорость, направление движения (путевой угол) а также дополнительная информация. В целом наблюдения СРНС можно представить в виде:

z CPHC ⁽ t ) = x ⁽ t )

( t ) ,

+ ^ СРНС

где zСРНС = ⎡⎣xи, yи, vи,ϕпи ⎤⎦T – вектор полученных с приемника СРНС значений координат xи, yи, скорости vи и путевого угла ϕпи объекта; x = [x, У, v Фп ] — реальные координаты объекта; ε= ⎡⎣εx,εy,εv,εϕп ⎤⎦ – вектор погрешностей наблюдений. Значения погрешностей εx,εy,εv,εϕп часто можно представить в виде белого гаус- совского шума со спектральными плотностями Nε,Nε, Nεv, Nεϕпсоответственно.

Инер ^y циальная система представляет собой совокупность датчиков ускорения (акселерометров) и угловой скорости (гироскопов), ориентированных определенным образом в пространстве. Данные с этих датчиков позволяют получить вектор ускорения подвижного объекта:

zинc (t) = a ( t ) + ^инс ( t ), где ZИНС = [aNu, aEu ]T - вектор ускорений полученный путем наблюдения показаний ИНС, a = [aN, aE ]T -реальныесевернаяивосточнаясо-ставляющиеускоренияобъекта, £ИНС = [£ aN, £ aE ]T – погрешности измерений ИНС. εaN,εaE будем аппроксимировать белым гауссовским шумом со спектральными плотностями NεaN = NεaE .

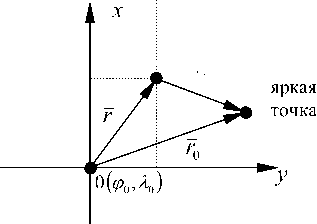
Рис. 1. Преобразование наблюдения ГАС в используемую прямоугольную систему координат

При помощи ГАС определяется пеленг и дальность до яркой точки. При этом вектор наблюдений можно записать следующим образом:

^z ГАС

⎡p⎤₊⎡ε p ^⎢⎣D ^⎥⎦ ^⎢⎣ε D

где Z ГАС = [ р и , D _u ] T , p, D - истинные значения пеленга и дальности до яркой точки, ε _p , ε _D – погрешности измерений – белые гауссовске шумы со спектральными плотностями N _εp, N _εD соответственно.

Пересчет наблюдений в прямоугольную систему координат показан на рис. 1. На этом рисунке обозначено: r – радиус-вектор определяющий местоположение корабля; rи – измеренный ради- ус-вектор от корабля до яркой точки; r0 – радиус-вектор, определяющий положение яркой точки.

Местоположения объекта по полученным наблюдениям ГАС (см. рис. 1) определяется следующим соотношением:

r = r _ r или x =D0⋅cos p0-D⋅cos p, y=D0⋅sin p0-D⋅sin p.

Оптимальные алгоритмы комплексирования

Будем предполагать, что производятся косвенные наблюдения отклонений от точки позиционирования координат x(t), y(t), ф(t) и их производных vx (t), vy (t), о(t) с помощью СРНС, ГАС и ИНС. Запишем модели наблюдений в следующей форме. Для СРНС xu(t) = x(t) + Sx (tX vxuc (t) = vx (t) + Svx (t),

У и ( t ) = y ^{( t} ) ^{+ S} y ^{( t} X vy uc ^{( t} ) = v y ^{( t} ) ^{+ S} vy ^{( t} X     ⁽¹⁾

x(t) = x 1 cos ф - y 1 sin ф ; y ( t ) где

= x 1 sin ф + y 1 cos ф ;

£ x ( t ), £ _y ( t ) и £ vx ( t ), £ vy (t) — нормальные независимые случайные величины со спектральными плотностями N _c и N _vc соответственно. Наблюдения ГАС записываются с помощью нелинейных моделей

Д ия ) = ^/ ( ^{x ( t} ) ⁺ d x ) ^{2 +} ( y ^{( t} ) ⁺ d y ) ^{2 +} E Д ^{( t} ),

( y ( t ) + d y^л

П и ( t ) = acrtg        Г ^{+ E} П ^{( t} ),

( x(t) + dx J где £д (t) и £П (t) - независимые нормальные случайные величины со спектральными плотностями NД и NП соответственно; dx=Д0cosП0, dy=Д0sinП0. В рассмотренном случае наблюдения целесообразно представить в виде вектора z(t) = (xu vxuc Уи vyuc Ди Пи vxuu vyuu )T . Введем также x (t) = (x(t) vx (t) y(t) vy (t)) -вектор оцениваемых параметров;

6 (t) = £ £ £ £ £n £n £ £ ) - BCK-x vx y vy Д П vxu vyu тор помех с корреляционной функцией B(t) = M {y (t) 0 T (t - т)} = NS(т), где 5(t) -дельта-функция, а N – (8×8) диагональная матрица спектральных плотностей белых шумов.

В приведенных обозначениях уравнение состояния запишется в виде векторно-матричного дифференциального у равнения:

-- = Ax ( t ) + ^ ( t ), (3) dt

⎛0100⎞ ⎜⎜0000 где A = ; ⎜0001 ⎜⎝0000⎠ T ^ (t) = ( 0 ^x (t) 0 ^y (t) ) - вектор случайных воздействий, которые для простоты представля-

ются в виде белого шума с заданной спектральной плотностью.

Для рассмотренной векторной нелинейной модели (3) воспользуемся квазилинейным приближением [7]. В этом случае уравнение фильтрации запишется в виде dx                     dhT (-x(t)) , r-1

— = ^- Ax ⁽ t ) + P ⁽ t )           N ( z ( t ) ^- h ( x ( t ) ) ) с

^dt                                  ^v.x(t )

начальными условиями xx ( t 0 ) = 0 и P ( t₀ ) = 0 при точном определении координат в начальный момент времени t=t ₀ . При этом уравнение для ковариационной матрицы ошибок имеет следующий вид [1]:

dP^ = AP ( t ) + P ( t ) A T + N_e -

- ^P ( t )

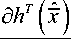
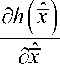
^P ( t ) .

Записанные соотношения с учетом начальных условий полностью определяют алгоритм квазилинейной фильтрации вектора состояния x (t) на основе наблюдений ГАС, спутниковой и инерциальной систем. При этом скоростные компоненты vx (t) и vy (t) оцениваются косвенно на основе приращений координат, а «коэффициентами усиления» соответствующих каналов фильтрации служат нормированные взаимные ковариации ошибок фильтрации, являющиеся недиагональными элементами матрицы P(t).

Наиболее простые процедуры фильтрации реализуются, если положить П0 = 0 (dx = Д0, dy = 0) или П0 = П|- (dx = 0, dy = Д0). В последнем случае пеленг из точки позиционирования на яркой точ-π ке составляет Пп = — .

При небольших отклонениях от точки по- зиционирования х<<До получим, что разность Ди - Д ( x) = У ( t ) - y (t ) + 5Д ( t ) дает прямую поправку в канал определения координаты y(t).

∂ Д

При этом — = 1 и оценивание координаты у осу-

∂y ществляется в режиме, близком к линейному. В этих же условиях основную информацию об из- менении координаты x дает применение пеленга

n(t). Действительно, Пи - П (x) = arctg x (У + До) - x (У) xx + (y + До)(y + До)

^{+ e} n ( t ) .

где tg ( П и - П ( ^x ) ) =

tgⁿ u - tgⁿ ( x ) 1 + tgn u tgn ( x )

При малых ошибках оценивания y≈ yˆ и малых отклонениях x, y <<  Д ₀ от точки позиционирования П -П^х^ = ( x-x ) + е ( t ) и с уче-

∂ П     1        ^Д 0

том ≅- получаем квазилинейный канал ∂ xД ₀

оценивания координаты x , основанный на вычислении взвешенной невязки:

∂ П _П

∂x ^u

- П(x)) -     "Г(x - x)+ еn(t)

Д ₀ ⎝ Д ₀

Анализ показывает, что в рассмотренных схемах комплексирования могут быть эффективно использованы линейные алгоритмы оценивания, основанные на линеаризации исходных уравнений наблюдения и состояния. Линейные алгоритмы в дискретном времени являются основой для создания реальных навигационных комплексов, работающих в режиме динамического позиционирования и объединяющих различные средства извлечения информации. Рассмотрим построение и анализ алгоритмов комплексной обработки данных в дискретном времени.

Для записанных моделей наблюдений и закона изменения вектора состояния x (1) известен оптимальный алгоритм фильтрации [7]:

-df = ^{p (} t ⁾ c ^T V ^{- 1 c} ( cz ( t ) - xx ( t ) ) ,        (4)

где P ( t )– матрица ковариаций ошибок оценивания;

Ax 0 Bx 0 0 0 0 A 0 B 0 0 c= 0 y 0 0 y 0 1 0 - матрица преобразо- 0 0 0 0 0 1 вания наблюдений вектора z ; Ах, Вх, Ау, Ву -весовые коэффицинеты точечного комплексирова-ния величин Xuj с и yui с yri. Данные коэффициенты целесообразно выбрать следующим образом:

A x =	σ Г 2 x		B x =	σ x 2
	^ 2 x +	σ x 2		° 2 х +	σ x 2
A y =	σ Г 2 y		B у =	σ y 2
	°" Гру +	° ’		° Гу +	σ y

Матрица ковариаций ошибок оценивания P _i по главной диагонали будет содержать дисперсии ошибок о ценивания соответствующих величин вектора x _i . Учитывая, что дисперсии шумов наблюдений постоянны, в фильтре Калмана будет наблюдаться установившийся режим, при котором матрица P _i = P _i-1 =P . Данные значения матрицы P _i устанавливаются, как правило, уже после нескольких первых итераций работы алгоритма.

Исследование эффективности рассмотренных алгоритмов

При использовании линейных алгоритмов фильтрации нелинейная зависимость от наблюдений дальности и пеленга проявляет себя в ковариационных зависимостях наблюдений декартовых координат. Кроме того, после функционального преобразования наблюдений дальности и пеленга в наблюдения координат положения объекта z _x , z _y появляются негауссовские шумы, которые снижают точность оценок линейного фильтра Калмана. Таким образом, существует задача исследования определения влияния негауссовского характера помех на точность построения оценок линейными алгоритмами.

Для данной задачи исследования в качестве модели движения объекта использовалось авторегрессионное уравнение первого порядка:

• x i = r x x i -1 ⁺ ^ xi ^, .

• 1                            i = 1,2,...,

yi = ry yi-1 + ^yi, где rx,ry – коэффициенты корреляции между соседними отсчетами соответствующих случайных процессов; ξxi,ξyi – независимые гауссовские СВ с нулевым средним и дисперсией σξ2 . В режиме динамического позиционирования начальные координаты известны точно и y1 = x1 = 0 . Следовательно, дисперсия ошибок оценивания P1 = 0 и Pэ1 = 0 .

При моделировании наблюдения {Дz} по дальности и пеленгу {Пz} формировались на основе вычисленных значений {ху }, {yj } с использованием формулы (2). Полученные величины использовались в нелинейном алгоритме качестве исходных данных для вычисления оценок вектора состояния xi на текущем шаге. В случае линейной фильтрации наблюдения декартовых координат {zxi}, {zyi} вычислялись на основе {Д .} и {nzi}. Используя полученные выражения, находились оценки вектора состояния xi на основе линейного фильтра Калмана с помощью линейного алгоритма (4).

На рис. 2а,б представлены результаты моделирования линейного и нелинейного фильтров Калмана при разных значениях дисперсии шума наблюдений и разных значениях дисперсии порождающего шума σ _ξ ^{2 .}

Анализ полученных данных показывает близкие теоретические значения дисперсий ошибок оценивания для рассмотренных алгоритмов и экспериментальные значения дисперсий, вычислен-ныхпутемусреднения1000реализацийслучайных процессов. Полученные результаты показывают незначительное влияние негауссовского характера помех на точность построения оценок по наблюдениям сферических координат. Так же следует отметить, что изменение дисперсии σ _ξ ² влияет как на величину дисперсии ошибок оценивания, так и на длительность переходного процесса. Чем меньше σ _ξ ² , тем дольше переходный процесс фильтра.

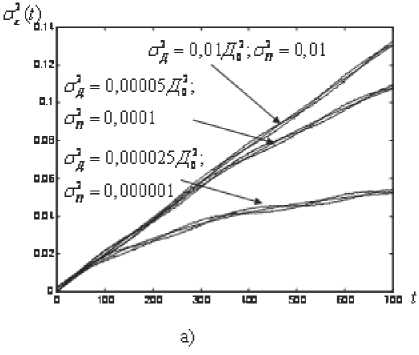
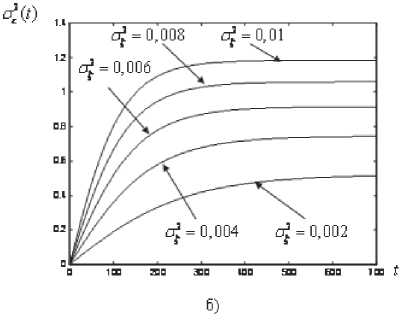
Рис. 2. Результаты моделирования линейного и нелинейного фильтров

Выводы

Использование линейных алгоритмов оценивания положения объекта по совокупности наблюдений ИНС, ГАС и СРНС не приводит к заметному ухудшению качества построенных оценок. В то же время линейные алгоритмы легко реализуются на ЭВМ при помощи современных языков программирования и обладают достаточно высоким быстродействием, что позволяет успешно использовать их в системах реального времени.