Алгоритмы трассирования в системе территориального проектирования

В настоящей работе рассматриваются алгоритмы трассирования коммуникаций различного назначения, используемые в Системе проектирования Генеральных схем обустройства. (СПГСО) [1, 2]. Это нефтепроводы сбора, и транспорта, нефти, водоводы высокого и низкого давления, дороги и другие нефтепромысловые коммуникации. В зависимости от способа, представления территории в СПГСО разработаны и используются различные алгоритмы трассирования.

В случае наличия на территории запретных зон для прокладки коммуникаций, представленных фигурами второго порядка (круги, эллипсы), разработан алгоритм трассирования, основанный на. методе локальных вариаций [3, 4].

Если территория представлена квадратной сеткой категорийиости, рассмотрены одноуровневый и двухуровневый алгоритмы нахождения оптимальной трассы, основанные на. применении модифицированного алгоритма. Дейкстра. [5]. Также рассмотрен случай представления территории треугольной сеткой категорийиости.

Если запретными областями для проведения коммуникаций являются многоугольники или ломаные, рассмотрен специальный алгоритм трассирования, основанный на. использовании «зон видимости вершин».

2.    Применение метода локальных вариаций при трассировке коммуникаций

Если на территории заданы запретные области для проведения коммуникаций, — озера, населенные пункты, реки, овраги, то для решения задачи трассирования можно применить метод локальных вариаций. Будем без ограничения общности полагать, что запретные области представлены фигурами второго порядка — кругами и эллипсами, хотя их представление другими фигурами сущности метода не меняет.

Рассмотрим основную идею метода. На рис. 1 показаны точки А и Б, которые нужно соединить оптимальным способом. При этом известны запретные зоны для проведения коммуникаций, представленные фигурами второго порядка (круги, эллипсы).

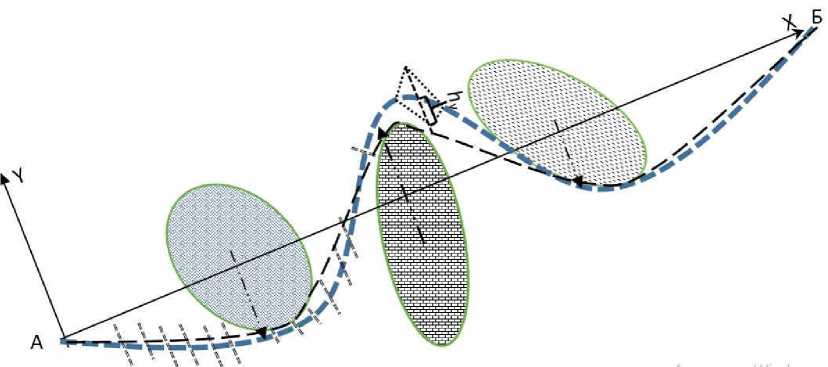
Рис. 1. Метод локальных вариаций. Начальное приближение и его стягивание к оптимальному

Введем систему координат с осью X , направленной из точки А в точку Б и будем искать решение в этой системе координат. Разобьем отрезок АБ на п равных частей точками Хк = к • һ, где к = 1, 2, 3,..., п, а һ = La/п. Для каждого Хк нужно определить значение Ук, для которого полученный путь по ломаным определяет оптимальный путь.

Первоначально строится допустимое приближение, которое не проходит через запретные области.

Для этого для каждой запретной области, через которую проходит начальное положение трассы, она сдвигается произвольным образом за границу области в сторону ближайшей границы относительно ее центра, как показано на рис. 1.

Подсчитываем длину этого пути, которая является суммой длин по всем отрезкам ло маной:

п l = £һЖк.

к=1

При изменении значения У к ^в какой-либо к-й точке на величину һ у длина нового пути изменится на длину новых отрезков минус длину старых:

AL = 1 ( х к - 1 ,У к - 1 ,Х к ,У к - һ у ) - 1 ( х к ,У к - һ у ,Х к ₊ 1 ,У к+1 ) - 1 ( х к - 1 ,У к - 1 ,Х к ,У к ) -

- 1 (_ Х к ,У к ,Х к+1 ,У к+1 ) .

Если окажется, что AL < 0, т.е. новый путь короче старого, то старая точка (хк, Ук) заменяется на новую ( х к ,У к — һ у ). Вели чину һ у будем называть шагом варьирования.

Если AL > 0. то нужно по этой же схеме рассмотреть точку ( х к ,У к + һу)■ Эта, операция проделывается для всех к, кроме конечных точек к = 0 и к = п. При этом при переходе от точки Х к к точке Хк+i значение длины на этом отрезке уже вычислялось и может быть использовано. В результате за. один просмотр траектория может отклониться от старой на.

величину һ_у в каждой из промежуточных точек. Эту операцию нужно повторять до тех пор, пока все у^ не перестанут изменяться, т.е. до тех пор, пока варьирование в каждой точке будет оставаться положительным. В этом случае задача для всех точек х ^ и данного шага варьирования һ_у считается решенной.

Наличие запретных областей не является препятствием для применения метода, так как при попадании варьируемой точки в запретную область приращение AL считается положительным и не будет принято.

При сходимости метода с шагом һ_у нужно продолжить процесс с шагом h_y/* 2 и т.д. Затем для повышения точности решения рекомендуется уменьшить шаг h_x по оси А и с этим новым h_x начать процесс заново.

На рис. 2 представлено применение метода локальных вариаций в Системе проектирования Генеральных схем обустройства для трассировании магистральных водоводов при решении задачи размещения насосных станций Федоровского нефтяного месторождения.

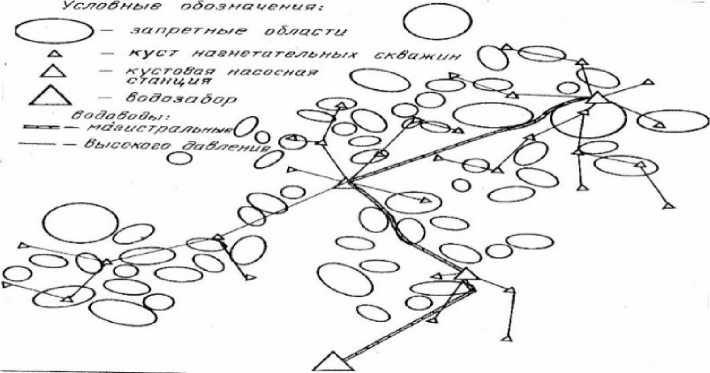
Рис. 2. Схема, водоводов Федоровского месторождения

3.    Алгоритмы трассирования на сетке категорийности территории

Территория представляется прямоугольной сеткой - матрица ||С|| размером mxn, состоящей из квадратов со сторонами I, для каждого из которых известна стоимость проведения единицы длины коммуникации с ц. Необходимо определить трассу наименьшей стоимости между двумя заданными точками А и В, находящихся в центре соответствующих элементов сетки категорийности.

Обозначим через r ij потенциал элемента ( ij ) сетки категорийности, равный текущему значению расстояния от точки А до точки ( ij ) — центра (ij)-ro квадрата.

3.1.    Одноуровневый алгоритм трассирования

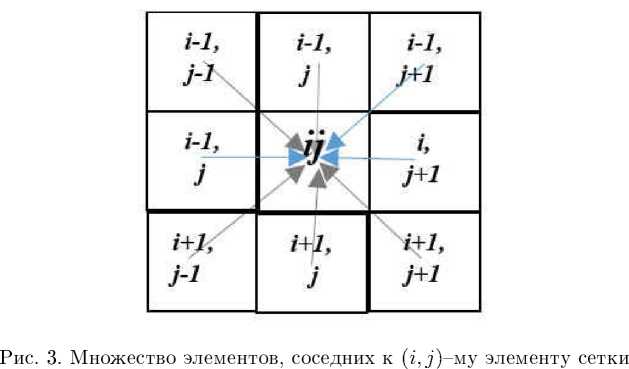
В одноуровневом алгоритме трассирования потенциал каждого элемента сетки p ^j матрицы ||Д| определяется как минимальная стоимость проведения трассы от соседних элементов сетки до текущего элемента сетки ( ij), где под соседними элементами сетки подразумеваются такие элементы сетки, индексы ( р, q ) которых отличаются от текущего индекса ( ij ) не более чем на единицу, и не выходящие за границу области. На рис. 3 представлено множество элементов сетки, соседних к ( i,j )-му элементу сетки категорийности. Функция «трассирования» Fr ( i,j ) определяет на каждом шаге алгоритма способ расчета очередного элемента матрицы ||Д|.

Fr(i,j) — min(pj±iу + (ct±i,j+ct,j)/2, p-i,j±i + (Cjj±i+ Ci,j)/2, pt±i,j±i + (Ci±iy±i+с«у) • V2/2) • I при 1 6 i ± 1 6 m, 1 6 j ± 1 6 n.

В начале работы алгоритма все элементы матрицы ||Д||, размерностью тхп полагаются равными большому числу М, а элемент p-iAjA = 0.

На рис. 4 представлена блок-схема алгоритма трассирования.

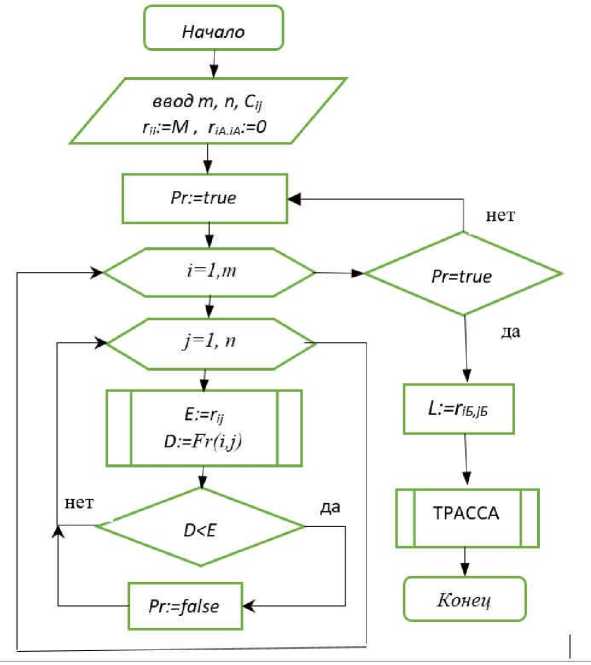
Рис. 4. Блок-схема, алгоритма, трассирования

Процедура. ТРАССА восстанавливает трассу от А до Б. Для этого в процессе работы алгоритма в специальном массиве размерностью т хп для каждого элемента сетки запоминается номер элемента его окрестности, на котором достигается минимум функции Fr ( i,j ). После этого трасса восстанавливается по этому массиву, начиная с элемента ( iB,jB y

3.2.    Двухуровневый алгоритм трассирования

В двухуровневом алгоритме трассирования соседними элементами считаются не только элементы первого, прилегающего к элементу ( i,j ) слоя, но и, как показано на рис. 5, некоторые элементы второго слоя (не выходящие за границы области).

Рис. 5. Серым цветом выделены соседние к ( i,j ) элементы сетки

Таким образом, всего соседних элементов второго уровня будет 16, если элемент ( i,j ) находится внутри области, 9 — если он лежит на ее границе и 5, если он находится в угле области. Отметим, что остальные элементы второго уровня будут просмотрены при просмотре элементов i ± 1, j ± 1 первого уровня. Вместо функции Fr ( i, j) в двухуровневом алгоритме используется функция

Grr ( i,j ) = тт((дщд + ( c i ± i,j + c^ j )/2, ± i + ( c i,j ± i + Gj )/2, ± i,j ± i + (c^±i,j±i + c^ j )x

X ^{2/2 /2,} V i ± 2,j ± 1 ⁺ ( ^c i ± 2,j ± 1 ^{+ c} i ± 1,j ± 1 ⁺ Cj±1,j ^{+ c} i,j ) • л/б/^4,

Vi±1,j±2 + (ci±i,j±2 + ci±i,j±i + Cj,j±i + ci,j) • V5/4) • I при 1 6 i ± 2 6 m, 1 6 j ± 2 6 n.

На рис. 6 представлены трассы, полученные по одноуровнему и двухуровнему алгоритмам трассирования, а также трассы, близкие к оптимальной.

В табл. 1 представлены стоимости коммуникаций по различным категориям территории.

Т а б л и ц а 1

Стоимость единицы длины трассы в зависимости от категории территории

Тип категории территории
Стоимость проведения трассы	1	2	3	6

В табл. 2 представлены характеристики трасс и их отображение.

Т а б л и ц а 2

Характеристики трасс

	Одноуровневая схема	Двухуровневая схема	Близкие варианты
Длина	38.9	35.5	15.7	17.1	11.4
Стоимость	46.6	46.3	50.8	50	50.3
Вид	------►	----►		..........

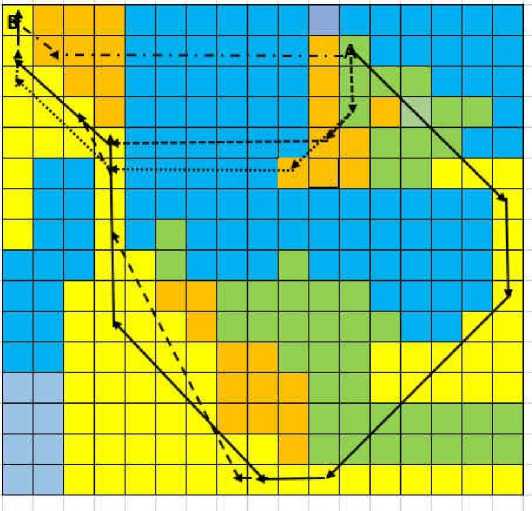
Рис. 6. Трассы, построенные по одпоуровпему и двухуровпему алгоритмам трассирования, и близкие трассы

3.3.    Трассирование в треугольной метрике

В некоторых случаях хорошие результаты можно получить при использовании треугольной метрики представления территории. Это также актуально при проектировании печатных плат. В этом случае территория представляется рядами равносторонних треугольников прямой (основаниями вниз) и обратной (основаниями вверх) ориентации, каждый из которых имеет шесть соседних элементов, как показано на рис. 7. В этом случае функция трассирования Tr ( i,j ) будет иметь вид

Tr ( i,j ) = min(^-ij + ( c i - i,j + a,j ) • 2/ V3,^ i,j ± i + ( c t,j ± i + a,j )x

• ^x V³/^2, ^г+і,у±і ⁺(^ct+i,j±2^{+ c}t,j) • ² • V^3,Фг+1,3^{+ (c}i+i,j^{+ c}t,j) • д/3^/2) • ^

4.    Трассирование при запретах в виде многоугольников и ломаных

при 1 6 i ± 1 6 m, 1 6 j ± 1 6 n.

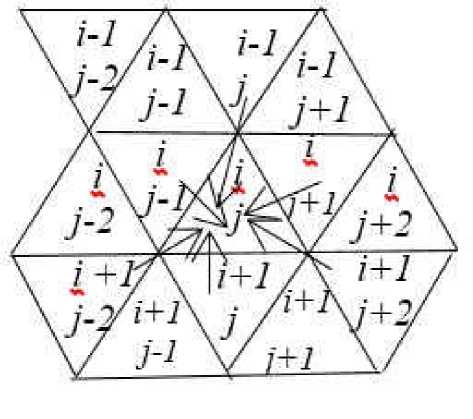
Рис. 7. Треугольная метрика. Соседние к (i, j)-My элементы

Также возможно использование реперных точек не в центре треугольников, а его вершинах, как показано на рис. 8. На рис. 8 представлены примеры трасс в треугольной метрике, с реперными точками в центе и в углах треугольников.

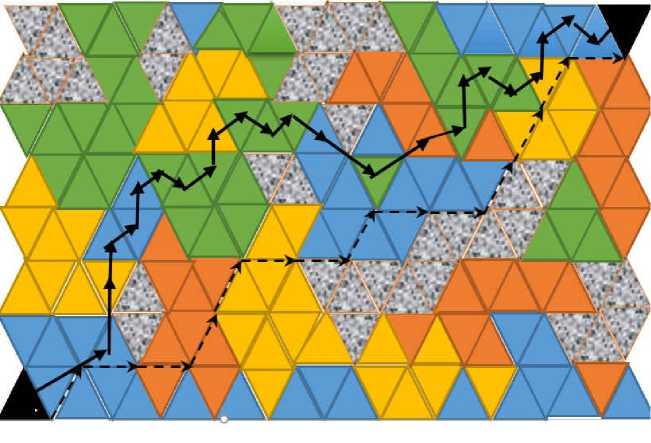
Рис. 8. Примеры трасс в треугольной метрике

Рассмотрим случай, когда запретные области для проведения коммуникаций представлены многоугольниками и ломаными, как показано на рис. 9. Нужно соединить точки А и Б кратчайшим путем, не пересекая запретные области (1, 2, 3,4) и (9,10,11,12) и ломаную (5, 6, 7 , 8).

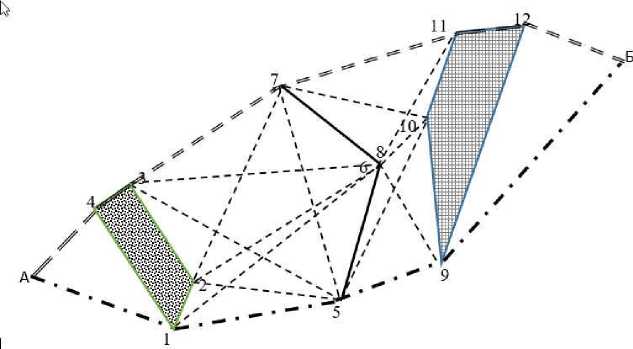
Рис. 9. Запретные области для проведения коммуникаций — многоугольники и ломаные

Алгоритм формирования кратчайшего пути при наличии запретных зон в виде многоугольников и ломаных

• 1)    Все вершины многоугольников, ломаных, начальная и конечная точки пронумеровываются. Отметим, что не концевые вершины ломаных для правильной работы алгоритма пронумеровываются с обеих сторон. Начальная точка получает 0-й номер, конечная — последний.

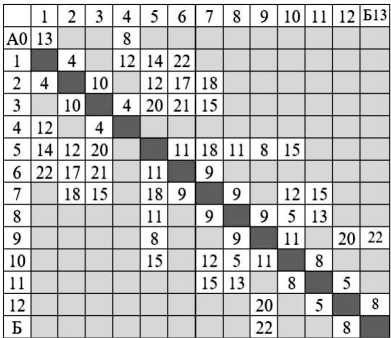
• 2)    Строится «матрица видимости». Для этого для каждого отрезка (гД) проверяется по правилам элементарной геометрии наличие пересечения этого отрезка со всеми границами областей и ломаных. Если таких пересечений нет, то вычисляется его длина l ij, которая и заносится в «матрицу видимости» — см. табл. 3.

Т а б л и ц а 3

Матрица видимости вершин

• 3)    По алгоритму Дейкстра [3] определяется длина кратчайшего пути от точки А до Б:

L_{on т} = 8 + 4 + 12 + 15 + 5 + 8 = 52 .

• 4)    Восстанавливается трасса кратчайшего пути. Маршрут: А-4-3-7-11-12-Б. Можно восстановить «близкий маршрут»: А-1-5-9-Б длиной +б_лизкая = 13 + 14 + 8 + 22 = 57.

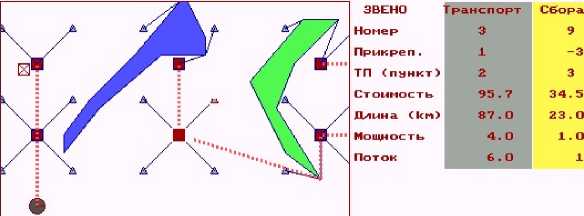
На рис. 10 представлена схема размещения замерных установок при наличии запретных зон — многоугольников.

пункты:   11 зі 5; в; 8: ю;	потр э;		ю;і5;іб :
Л		л
	Проект	Пункты	Транспорт	Сбор
Нонер/чисио (п,ТП,потр.)	1	6	2	18
Стоимость	1047.2	60.1	246.1	741. О
Длина сетей <км>	741 . О		247 . О	494.0

Номер/число <п,ТП,потр.)	3	1	1	4
Стоимость	243.7	10.0	95.7	138 . О
Длина сетей <Км>	179 . О		87 . О	92 . О

Рис. 10. Схема, размещения ЗУ. Запреты — многоугольники

Заключение

Описанные алгоритмы реализованы в Системе проектирования генеральных схем обустройства (СПГСО) и многократно использовались при проектировании обустройства нефтяных месторождений Западной Сибири.