Алгоритмы векторного управления электромеханического дебалансного вибромодуля без предварительного намагничивания асинхронного двигателя

В настоящее время электропривод с частотным преобразователем и асинхронным двигателем является главным типом регулируемого промышленного электропривода, серийно выпускаемого ведущими отечественными и зарубежными электротехническими фирмами.

При математическом описании асинхронной машины используются общепринятые допущения и ограничения [1]:

• •    Магнитная система машины не насыщена.

• •    Потери в стали отсутствуют.

• •    Фазные обмотки машины симметричны и сдвинуты на 120° (для 3-фазной машины).

• •    Магнитодвижущие силы обмоток и магнитные поля распределены вдоль окружности воздушного зазора по синусоидальному закону.

• •    Величина воздушного зазора постоянна.

• •    Ротор машины симметричен.

• •    Реальная распределенная обмотка заменена эквивалентной сосредоточенной, создающей ту же магнитодвижущую силу.

Главными компонентами асинхронного электродвигателя являются статор и ротор, которые отделены друг от друга воздушным зазором. Активную работу в двигателе выполняют обмотки и сердечник ротора [2].

Алгоритм двухканального управления

При синтезе системы векторного управления асинхронного электропривода одним из классических методов, например, методом подчиненного регулирования, управление будет осуществляться по двум каналам: каналу поперечной оси и каналу продольной оси. В данном случае необходимо предварительное намагничивание машины и последующее удержание потокосцепления ротора на номинальном уровне [5].

Данная структура позволяет осуществлять управление скоростью вращения дебалансов по двум каналам без предварительного намагничивания. Необходимым условием линеаризации является равенство постоянных времени двух каналов – канала потокосцепления ротора и канала поперечной составляющей тока статора. Здесь возникает еще одна проблема – контуры регулирования поперечной и продольной составляющей тока статора имеют одинаковое быстродействие, поскольку физически это один и тот же контур регулирования тока статора. Скомпенсировав действие ЭДС в каналах поперечной и продольной оси путем введения положительных обратных связей по ним, можно рассматривать контуры токов I_d и I_q как независимые друг от друга [13].

Управление электромагнитным моментом двигателя с использованием звена деления проиллюстрировано на рис. 1.

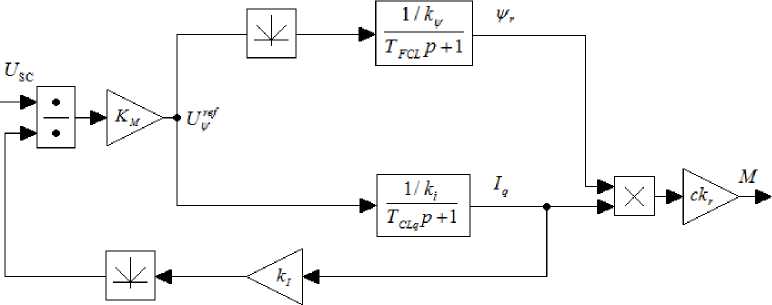
Рис. 1. Двухканальное управление электромагнитным моментом асинхронного двигателя

Fig. 1. Dual control electromagnetic torque induction motor

• На рис. 1 были приняты следующие обозначения:

U sc – выходной сигнал регулятора скорости;

K M – дополнительный усилитель;

U _ψ ^ref – напряжение задания потокосцепления ротора и тока I_q ;

k i – коэффициент обратной связи по току статора;

k _ψ – коэффициент обратной связи по потокосцеплению ротора;

T FCL – постоянная времени контура регулирования потокосцепления ротора;

T CLq – постоянная времени контура регулирования составляющей тока I q ;

ψ _r – потокосцепление ротора;

I q – поперечная (моментообразующая) составляющая тока I q ;

с = 2 p p ;

p p – число пар полюсов;

k r – коэффициент связи ротора;

М – электромагнитный момент двигателя.

Теория

Компенсация действия ЭДС осуществляется путем введения положительных обратных связей по ее составляющим.

Выражение для ЭДС в канале оси d :

e d = w ψ I q L σ e - k r ^d ψ ^r ,                                                                      (1)

dt где wψ – скорость вращения поля ротора, рад/с;

L _{σ e} – эквивалентная индуктивность рассеяния, Гн;

Выражение для ЭДС в канале оси q :

e_q =- w _ψ I_dL _{σ e} - w _ψ k_r ψ _r ,                                                                 (2)

где 1 д - продольная (намагничивающая) составляющая тока статора, А.

Поскольку в структуре присутствует звено деления, а также естественное произведение тока I_d на потокосцепление ротора, то возможность реверса в таком электроприводе отсутствует. Этот недостаток устраняется введением в канал продольной оси, а также канал обратной связи по току I_q определителей модуля [13].

С помощью синтеза регуляторов контур регулирования тока I_d настраивается на частоту Ω _CLd . Контуры регулирования тока I_q и потокосцепления ротора настраиваются на частоту Ω _FCL , на порядок меньшую, чем Ω _CLd [10].

Целью синтеза такой системы управления электромеханического дебалансного вибромодуля является иллюстрация очевидного достоинства – намагничивание электродвигателя [9]. В этом случае меньше номинального уровня в установившемся режиме. Потокосцепление ротора в установившемся режиме будет совершать колебания вокруг среднего значения, меньшего по сравнению с номинальным, амплитуда колебаний при этом также будет существенно меньше номинального значения потокосцепления ротора [14, 15].

Структурная схема электропривода дебалансного вибромодуля с двухканальным алгоритмом управления показана на рис. 2.

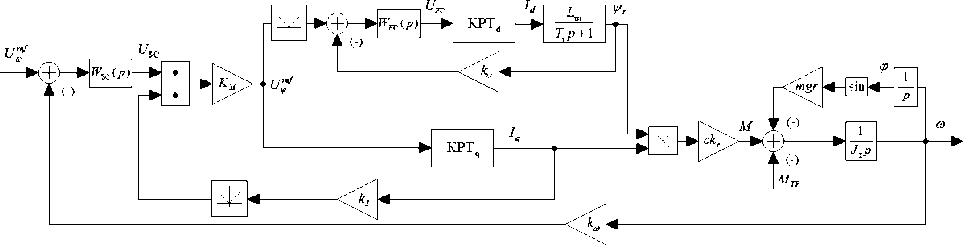
Рис. 2. Структурная схема электропривода системы управления дебалансного вибромодуля Fig 2. The structural diagram of the electric control system unbalance vibration module

На рис. 2 были приняты следующие обозначения:

U _w^ref – напряжение задания скорости;

U_FC – выходной сигнал регулятора потокосцепления;

W SC ( p ) - передаточная функция регулятора скорости;

W_fC ( P ) — передаточная функция регулятора потокосцепления ротора;

КРТ _d – контур регулирования тока I d ;

L_m – взаимная индуктивность обмоток статора и ротора;

T_r – эквивалентная постоянна времени роторной цепи;

КРТ _q – контур регулирования тока I_q ;

к _ю - коэффициент обратной связи по скорости;

m – масса дебаланса;

g – ускорение свободного падения;

r – эксцентриситет дебаланса;

Ф - угловое положение дебаланса.

Дополнительный усилитель K_M устанавливает однозначное соответствие между уровнями сигнала U_SC и значениями электромагнитного момента М . Данный усилитель рассчитывается по формуле

М

K =----max— к - к .(3)

M U max - ck r ^{v 1}

Составим математическое описание системы управления. Выражение для сигнала задания тока I q и потокосцепления v r :

U= Km - UC.(4)

k ^- I q

Тогда потокосцепление v r определяется так:

Vr = U^ . WfCl (p),(5)

где W_fCl ( p ) - передаточная функция контура регулирования потокосцепления ротора.

Ток I_q определяется аналогичным образом:

Iq = U^ - WcLq (Р ) ,(6)

где W_CLq ( p ) - передаточная функция контура регулирования тока I q .

Электромагнитный момент двигателя:

M = ckr - Iq -vr.(7)

Если пренебречь инерционностью контура тока I_d по сравнению с инерционностью внешнего по отношению к нему контура потокосцепления, то

M = ck, -1. - Km - USC-Wraip] = ckr" KM - Usc—1^^ • r q M ki Iq FCL (PI ki SC Tfclp +,1 ,

Кроме особенностей математической модели асинхронного электродвигателя в настоящей работе требуется учитывать особенности вибромодуля как нагрузки. В данном случае можно выделить две главные особенности – большой момент инерции маховых масс электропривода, а также синусоидальную зависимость момента сопротивления от угла поворота ротора.

Применимость такой структуры управления к электромеханическим дебалансным вибраторам можно показать с помощью компьютерного моделирования [3, 4].

Уравнение движения электропривода будет выглядеть так:

J^ — = M - M = M - MTp - mgr sin ф.(9)

" dt            c ТР

Суммарное силовое воздействие со стороны двух полумодулей дебалансного вибратора с учетом переменного характера скорости вращения дебалансов имеет следующий вид:

F^ = 2 mr fro2 cos ф + -^ sin ф|.(10)

V

Здесь можно выделить две составляющие:

• 1)    центробежные силы mr ro ² cos ф ;

~dro. „

• 2)    тангенциальная составляющая полного ускорения дебаланса mr —sin ф . dt

Передаточная функция регулятора тока выбрана следующей:

W ccd ( P ) = K ccd T : e^{p +} - .                                                           (11)

^T a e P

Неизвестным параметром регулятора является Kccd . Передаточная функция замкнутого кон- тура регулирования тока Id с таким реулятором имеет вид

WCLd ( P )“

1 k i     _,

T CLd p ^{+ 1}

где TcLd = —-— - эквивалентная постоянная времени контура регулирования тока Id, которая Q CLd определяется исходя из принятой полосы пропускания QCLd контура регулирования тока, которая определяется исходя из принятой полосы пропускания контура регулирования тока. Для того чтобы разделить движения контуров, принимаем, что полоcа пропускания контура регулирования тока QCLd должна быть на порядок выше, чем частота сейсмического сигнала Q, т. е. QCLd >(6^10)-Q .

Тогда можно из выражения для T_CLd

_T = R 1 ^T a e

CLd

Kccd K fcki определить коэффициент передачи Kccd

K = RT e

.

ccd

T CLd K fc k i

Передаточная функция регулятора тока I_q выбирается аналогичным образом:

W ccd ( P ) = K ccd

^T a e P ^{+ 1}

^T a e P

Тогда передаточная функция замкнутого контура регулирования тока Iq с таким регулято- ром:

^WCLq ( P ) = ^k^ ,

T CLq P ^{+ 1}

где lCLqP =---- - эквивалентная постоянная времени контура регулирования тока 1 , которая q Q CLq                                                                             4

определяется исходя из принятой полосы пропускания контура регулирования тока QCLq. Для того чтобы разделить движения контуров, принимаем следующее:

Q CLq =Q, тогда из выражения следует:

_T =   R 1 T e

CLq

K ccq K fc k i

.

Определить коэффициент передачи K_ccq :

K = RT e ccq

T CLq K fc k i

.

Передаточная функция регулятора потокосцепления ротора выбирается так:

W FC ( ^p ) = K FC "^ P

T ₂ p

.

Тогда передаточная функция замкнутого контура регулирования потокосцепления ротора с таким регулятором:

W C ^L q ^{( P} ) T fcl P + 1,

где TFCL = —-— - эквивалентная постоянная времени контура регулирования потокосцепления, Q FCL которая определяется исходя из принятой полосы пропускания контура регулирования потокос цепления QFCL. Исходя из синтеза, принимаем QFCL = QCLq = Q .

Тогда можно из выражения для T_FCL

_T = kT

FCL

Kfcl^ kv определить коэффициент передачи KFC :

k i T 2

KFC     L к

T FCL L ц ^k v

.

Поскольку при решении поставленной задачи не требуется обеспечение астатизма по скорости, то контур регулирования скорости можно выбрать пропорциональным [2].

Если пренебречь инерционностью вложенных контуров по сравнению с контуром регулирования скорости, то приравнивая желаемую передаточную функцию к передаточной функции контура регулирования скорости:

W_s cP P ) • ck r 'K M • — • — SC        k i     к v J . P

1 к _ю

1 + WscPP ) • ck r ' K M • — • — • k o ^TSCL^{P +1}

SC       ki    кv J. P получим выражение для определения передаточной функции регулятора скорости

Jy, " к " k\« w cp p ) = К  =----i v---

SC ( ) SC   T scl . ck r . Km . к _ю

.

Поскольку передаточную функцию контура регулирования потокосцепления приближенно можно представить следующим периодическим звеном

W ( p ) = ^ k ^,

^M , Tfcl P + 1

то можно заключить, что линеаризация математической модели асинхронного двигателя (при условии работы в пределах ограничений регуляторов, с помощью звена деления и дополнительной обратной связи по току I ) является осуществимой. Кроме того, система управления асинхронным электроприводом в этом случае не требует предварительного намагничивания электрической машины и отдельного управления по каналу d . Электропривод, при описании которого имеется допущение, что насыщение магнитной системы в нем отсутствует, называется ненасыщенным. Предположение такого допущения, например при описании электродвигателя в виде

замещения, позволяет получить простые формулы расчета и структурные схемы для моделирования, но, с другой стороны, при таком упрощении точность расчетов может оказаться недостаточной [6].

Насыщение проявляет себя только в изменении коэффициента, связывающего главный магнитный поток (полезный поток в зазоре) с намагничивающим током (током в намагничивающем контуре схемы замещения).

Структурная схема насыщенного асинхронного электродвигателя при ориентации системы координат по вектору потокосцепления ротора представлена на рис. 3.Структурная схема строится на основании уравнений:

p ψ 1 α = u 1 α - R 1 ⋅ i 1 α +ω 0эл ψ 1 β ; p ψ 1 β = u 1 β - R 1 ⋅ i 1 β -ω 0эл ψ 1 α ;

• - R ₂ ⋅ i _{2 β}

• pψ2 =-R2 ⋅i2α; ωp =

ψ ₂

• ψ 1 α -ψ m α       ψ 1 β -ψ m β

• i1α =                ; i1β =

L1σ

• ψmα =ψ2 -L2σ ⋅i2α; ψmβ = -L2σ ⋅i2β;

• -i2α = i1α -imα; -i2β = i1β -imβ;

imα = ( Lm′ ) ⋅ ψ mα ; imβ = ( Lm′ ) ⋅ ψ mβ ;

M _д = 32 p _п ⋅ψ ₂ ⋅ ( - i _{2 β} ) .

По уравнениям, описанным выше, получаем структурную схему асинхронного двигателя во вращающейся системе координат с учетом кривой намагничивания [13].

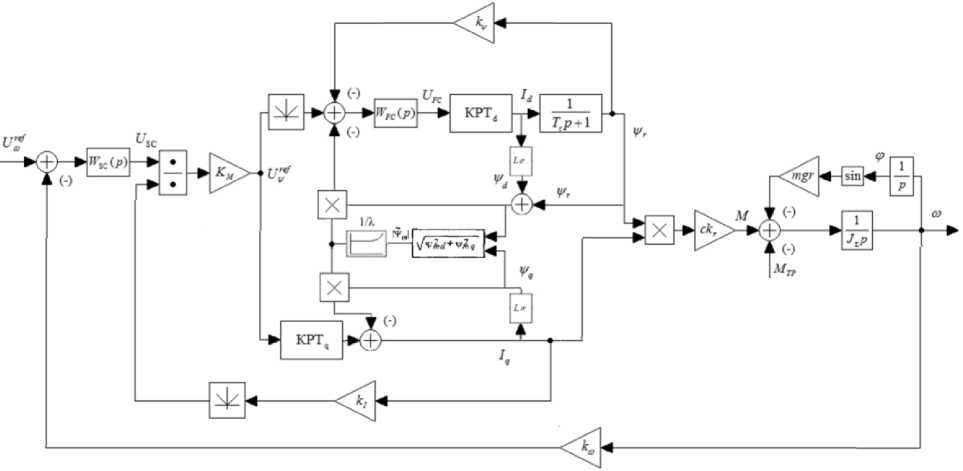
Рис. 3. Структурная схема насыщенного асинхронного двигателя при ориентации вращающейся системы координат по потокосцеплению ротора Fig. 3. Structural scheme of a saturated induction motor with orientation of the rotating coordinate system along the rotor flux linkage

Рассмотренная модель АД может использоваться для описания динамических процессов в асинхронном электроприводе с управлением от преобразователя частоты во всех типовых режимах регулирования переменных. За счет учета потерь в стали модель позволяет осуществлять точный анализ энергетических характеристик привода как в статике, так и в динамике.

В данной модели входными параметрами являются проекции вектора напряжения статора, а выходными – магнитный поток ротора, скорость двигателя, проекции токов статора, ротора, проекции потокосцепления статора, потокосцепление ротора, главное потокосцепление и роторная частота [7,8].

Результат моделирования

Исходными данными для проектирования системы управления электромеханического деба-лансного вибромодуля были амплитуда виброусилителя ( А ) и частота виброусилителя (Ω): А = 390 000 Н; Ω = 14 π рад/с. Ниже представлены параметры системы управления, которые использовались при ее синтезе и моделировании [13].

Параметры дебалансов:

• •    эксцентриситет дебаланса r = 0,2 м;

• •    масса дебаланса m = 500 кг.

Параметры выбранного асинхронного двигателя 4А280S10У3:

• •    номинальная мощность P_r = 37 кВт;

• •    номинальное фазное напряжение статора U 1 r = 220 В;

• •    номинальная скорость вращения n r = 590 об/мин;

• •    номинальный момент на валу двигателя M r = 600 Нм;

• •    максимальный момент на валу двигателя M _max = 1080 Нм;

• •    номинальный фазный ток I _{1 r} = 79 А;

• •    число пар полюсов p p = 5;

• •    коэффициент связи ротора k r = 0,937;

• •    активное сопротивление статора R 1 = 0,0835 Ом;

• •    эквивалентная постоянная времени статорной цепи T _{σ e} = 0, 024 c ;

• •    взаимная индукция обмоток статора и ротора L m = 0,0177 Гн;

• •    эквивалентная постоянная времени роторной цепи T_r = 0,2716 c;

• •    момент силы трения в подшипниках M _тр = 200 Нм;

• •    момент инерции электропривода, приведенный к валу электродвигателя J _Σ = 23,6 кг ⋅ м² ;

• •    коэффициент передачи частотного преобразователя K fc = 31,1.

Структурное моделирование было проведено в программном пакете MATLAB/Simulink.

В целях сравнительной оценки результатов синтеза системы управления с регулятором момента в виде звена деления (СРМ) была также синтезирована система подчиненного регулирования (СПР), обладающая аналогичными параметрами силовой части. [11] Результаты цифрового моделирования (графики переходных процессов скорости двигателя, момента, потокосцепления ротора и тока I d ) приведены в следующем пункте данной научной статьи.

Исследование системы с учетом кривой намагничивания

Из справочника по асинхронным электродвигателям известны табличные данные из справочного каталога Копылова [12] по исследуемому асинхронному двигателю 4А280S10У3, по которым производем построение кривой намагничивания в среде MATLAB:

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯДЕБАЛАНСНЫХ ВИБРОМОДУЛЕЙ

Моделирование алгоритмов управления проводилось в программном пакете MATLAB/ Simulink.

Имитационная модель электропривода дебалансного вибромодуля с двухканальным алгоритмом представлена на рис. 4.

Имитационное моделирование разработанной системы было проведено в программном пакете MATLAB/Simulink, в результате чего были рассчитаны ее динамические характеристики. Результаты моделирования представлены на рис. 5–9. Предполагается, что использование данной структуры управления позволит существенно снизить тепловые потери на намагничивание асинхронного электропривода дебалансного вибромодуля по сравнению с классическими системами, разработанными раннее.

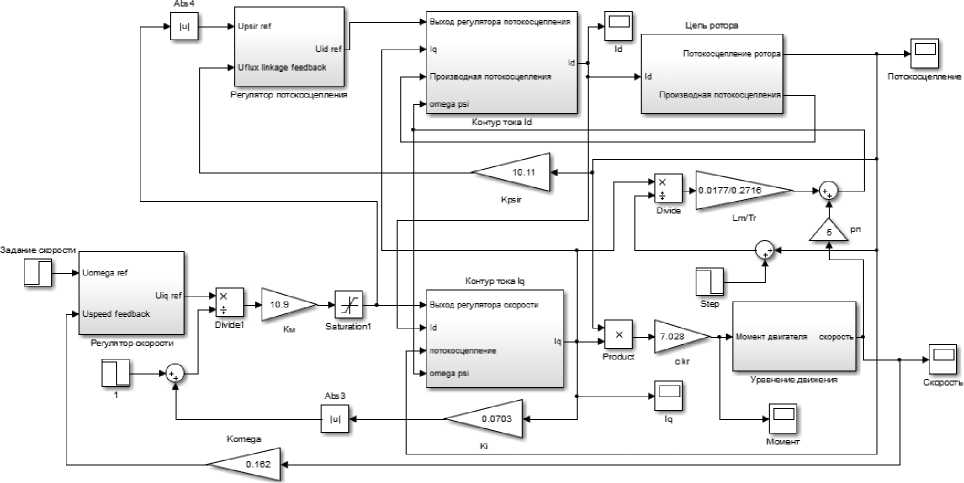
Рис. 4. Имитационная модель электропривода дебалансного вибромодуля с двухканальным алгоритмом Fig. 4. Simulation model of the unbalanced vibration module electric drive with a two-channel algorithm

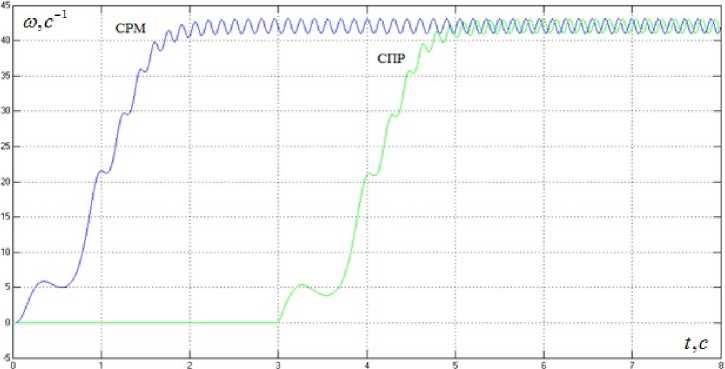
Рис. 5. Переходные процессы скорости дебаланса для системы с двухканальным алгоритмом Fig. 5. Unbalance rate transients for a system with a two-channel algorithm

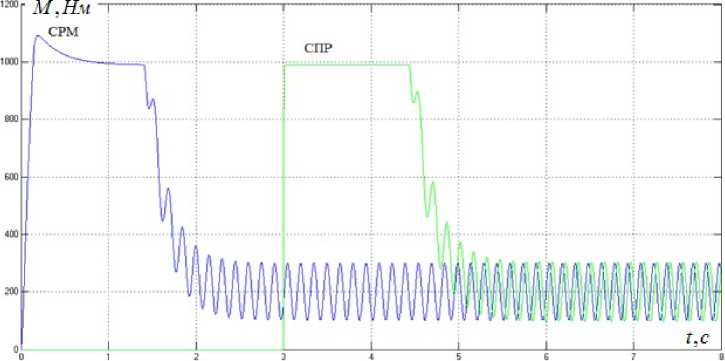
Рис. 6. Переходные процессы электромагнитного момента для системы с двухканальным алгоритмом Fig. 6. Transients of electromagnetic moment for a system with a two-channel algorithm

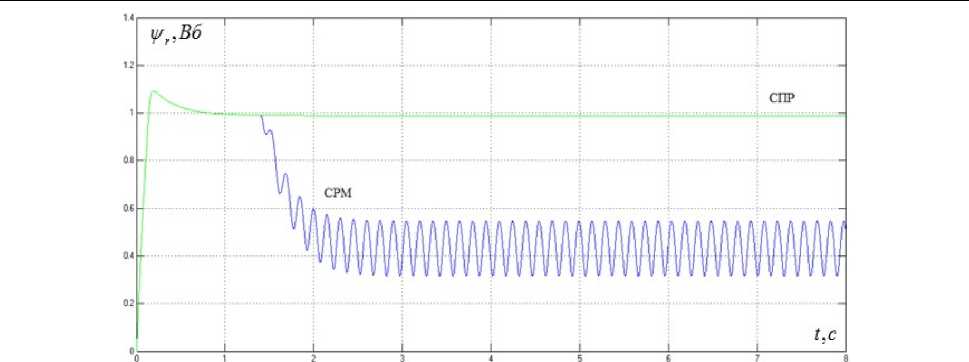
Рис. 7. Переходные процессы потокосцепления ротора для системы с двухканальным алгоритмом

Fig. 7. Rotor flux linkages for a dual-channel system

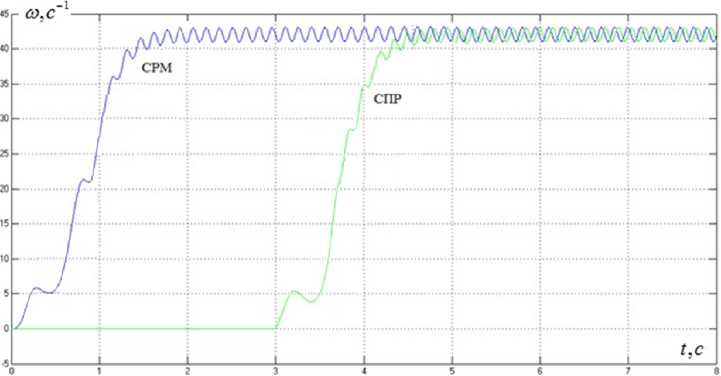
Рис. 8. Переходные процессы скорости дебаланса для системы с двухканальным алгоритмом с учетом кривой намагничивания Fig. 8. Unbalance rate transients for a system with a two-channel algorithm taking into account the magnetization curve

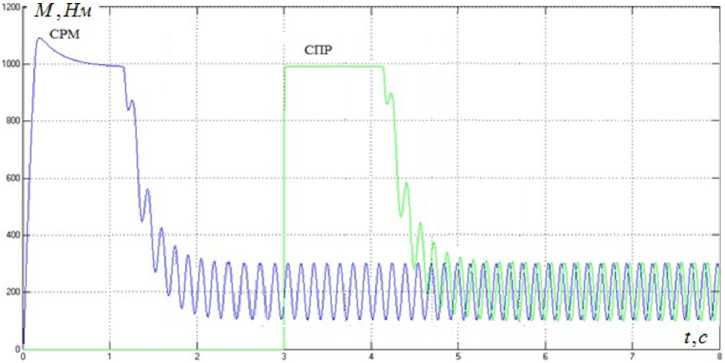
Рис. 9. Переходные процессы электромагнитного момента для системы с двухканальным алгоритмом с учетом насыщения

Fig. 9. Transients of electromagnetic moment for a system with a two-channel algorithm taking into account saturation

Выводы

Структурное моделирование построенной системы управления дебалансного вибромодуля было проведено в программном пакете MATLAB/Simulink.

В целях сравнительной оценки результатов синтеза системы управления с регулятором момента в виде звена деления (СРМ) была также синтезирована система подчиненного регулирования (СПР), обладающая аналогичными параметрами силовой части. Контур регулирования намагничивающего тока в обоих случаях настраивается на полосу пропускания f = 700 Гц, контур регулирования тока I q в СРМ был настроен на частоту 70 Гц. При этом частотный преобразователь представлялся безынерционным звеном.

Для исследований были произведены расчеты для асинхронного электродвигателя и регуляторов. Результаты цифрового моделирования, графики переходных процессов скорости двигателя, электромагнитного момента, потокосцепления ротора и тока I d для системы с регулятором момента в виде звена деления (СРМ) и классической СПР, обладающей аналогичными параметрами силовой части, показаны на рис. 5–9. В обеих системах осуществлялось задание на частоту сейсмического сигнала, равную 7 Гц. Поскольку система подчиненного регулирования предполагает предварительное намагничивание асинхронного двигателя, то в целях более наглядного представления результатов моделирования пуск двигателя в этой системе был осуществлен на 3 с позже, чем в системе с регулятором момента (СРМ). Учет насыщения магнитной системы при моделировании работы асинхронного короткозамкнутого двигателя позволяет на одну секунду раньше получить значения расчетного момента холостого хода и скорости вращения вала двигателя, чем в случае, не учитывающем это явление.