Алгоритмы выявления и устранения ошибок в базах знаний экспертных диагностических систем

В различных областях человеческой деятельности лица, принимающие решения (ЛПР), вынуждены работать в ситуациях, где их знания недостаточно полны, а будущие последствия принятых решений обладают значительной неопределенностью. В этих случаях они вынуждены полагаться на свой опыт и интуицию. С развитием вычислительной техники возникла идея создания экспертных систем, которые могли бы служить советчиками и консультантами для менее опытных руководителей. Задача построения таких систем возникла в двух направлениях исследований. Во-первых, в рамках работ по искусственному интеллекту появились так называемые экспертные системы [1]. Во-вторых, в рамках работ по принятию решений возникли системы поддержки принятия решений [2]. И те, и другие системы имеют в своем составе базу знаний (БЗ), в которой содержатся знания опытного эксперта.

В процессе формирования БЗ необходимо получить большой объем экспертной информации. Организация и проведение экспертного опроса требуют значительных трудозатрат как разработчиков, так и самих экспертов. БЗ должна удовлетворять многим требованиям, среди которых важнейшими являются обоснованность, полнота и непротиворечивость содержащейся в ней информации. Обоснованность БЗ определяется компетентностью эксперта, знания которого используются при ее построении. Полнота БЗ означает ее способность давать рекомендации (решения) во всех гипотетически возможных ситуациях в выделенной предметной области. Под непротиворечивостью БЗ обычно понимается ее способность гарантировать получение однозначного решения для любой рассматриваемой ситуации. Следовательно, необходимо предусмотреть средства для проверки экспертной информации и анализа ее непротиворечивости.

В настоящее время вопрос о способах оценки качества полученных экспертных знаний весьма противоречив. В многочисленных работах по экспертным системам, как правило, лишь отмечается, что качество экспертных систем зависит от полноты и совершенства их баз знаний [3]. Как правило, заполнение БЗ системы осуществляется посредством введения в нее данных об известных эксперту закономерностях, основных элементах и структуре взаимосвязей в изучаемой предметной области. Расширение БЗ выполняется в ходе работы эксперта с системой, нахождении им пробелов в БЗ и их последовательном заполнении (зачастую методами математической статистики, что не всегда корректно). При этом процесс формирования БЗ носит в целом фрагментарный характер, является трудоемким и не обеспечивает выполнения указанных выше требований.

Одним из видов систем, основанных на знаниях, являются диагностические системы, которые по своим функциям предназначены для помощи пользователю в разрешении следующей проблемной ситуации: по набору значений частных признаков, описывающих состояние объекта исследования, требуется определить, какими свойствами этот объект обладает. Базы знаний для решения таких задач должны содержать в себе решающие правила опытных экспертов, позволяющих строить классификацию всех возможных состояний объекта в предварительно структурированной проблемной области, классами которой являются подмножества состояний, обладающих одним и тем же свойством.

В работе предлагается новый подход к выявлению экспертных знаний для формирования БЗ диагностических систем.

Постановка задачи

Принять решение о создании БЗ диагностической системы, опираясь на экспертную классификацию, можно следующим образом.

Предположительно, объект исследования может обладать множеством характеристик P = {P q ,P i , -,P_l} - Согласно исследованиям, эти свойства можно обнаружить в его характеристиках с помощью значений М признаков (т = 1, М), которые характеризуют различные стороны объекта. Для каждого т-го признака существует множество возможных значений: Q m = {Q m₁ ,Q m₂ , -■,Ч_т п_т }, где п_т - число возможных значений т-го признака. Мы можем заметить то, что характеристики и возможные значения этих признаков сформулированы на естественном языке.

В Декартовом произведении А = Q_rxQ₂x .х Q_M содержится множество всех возможных состояний объектов, которые могут быть определены как возможные и в которых они могут обладать свойствами из множества P . Данное состояние а ; Е А можно описать с помощью вектора а ; = (а_и, a_i2,... , a_im), где a_im Е Q_m, т = 1, М.

На основе знаний эксперта необходимо определить наличие соответствующих свойств P для каждого состояния из A и, опираясь на эти знания, выстроить классификацию множества А = U i ₌₀K_t таким образом, чтобы каждое состояние а ; Е А относилось к определенному классу K i в случае, если оно обладает по мнению эксперта свойством Р. Класс К_о включает в себя состояния, при которых объекты не имеют ни одного из рассмотренных свойств [4].

Данные задачи могут быть сформулированы в зависимости от особенностей, которые будут влиять на ее постановку:

• -    в случае если объект в каждом из состояний а ; Е А имеет несколько свойств P , которые могут быть отнесены к одному из множества A , результатом классификации К_о,K_r, ..,K_L должно быть покрытие множества множественными частями;

• -    в случае если объект в каждом из состояний а ; Е А имеет возможность обладать только одним из свойств множества P , то результатом классификации должно быть разделение множеств A на классы L + 1;

• –    степень проявления свойств у объекта может быть различной в различных состояниях, которые относятся к данному классу, и тогда задача классификации будет дополнена требованием проведения экспертной оценки степени проявления свойств у различных состояний.

Экспертная классификация имеет дело с реальными задачами, которые имеют достаточно большой размер [3, 4]. Это может быть связано с большим количеством признаков и их возможных значений, которые могут быть определены. Как результат, можно сделать вывод, что непосредственная классификация экспертом всех состояний объекта, которая является простым и очевидным способом решения задачи, не представляется возможной. Проведение анализа отдельных ключевых правил эксперта, позволяющих классифицировать возможные состояния, требует определенных усилий и может быть трудоемким. Также не гарантируется полная и однозначная передача информации в случае, если они будут выявлены. При решении поставленной перед нами задачи необходимо разработать методику работы с экспертом, которая будет включать в себя систематизацию его классифицирующих правил и сокращение количества вопросов, на которые он должен будет отвечать. Кроме того, необходимо обеспечить проверку получаемой информации на соответствие ее стандартам и выявить возможные ошибки в ответах на вопросы.

Предлагаемый подход к решению задачи экспертной классификации основан на предположении о том, что степень отличности отдельных значений каждого признака для каждого свойства имеет свою собственную закономерность, которая не зависит от других признаков [4].

Допустим, что это можно описать так: если значения признака Q_m упорядочить по их особенной значимости для характеристики свойства P i , то это может привести к введению на Q_m транзитивного и антирефлексивного бинарного отношения (линейный порядок): r m : (q_{m s} , q_{m t} ) Е r m , если значение q_{m s} более характерно для свойства P i , чем значение q_{m t} .

Поясним это на примере выявления вызванной синхронизации/десинхронизации на электроэнцефалограмме. Электроэнцефалография (ЭЭГ) является широко распространенным методом получения сигналов головного мозга, для снятия которых используются электроды, расположенные на поверхности головы [5]. ЭЭГ активность, представляющая собой волны приблизительно одной постоянной частоты, называется ритмом, при этом наиболее выраженный в ЭЭГ ритм считается доминирующим. Процесс, выражающийся в формировании регулярной, упорядоченной ритмической активности и нарастании амплитуды колебаний, является синхронизацией ритма, а нарушение ритмичности протекания волновых процессов с замещением упорядоченной синхронной волновой активности колебаниями, менее регулярными, разной частоты и меньшей амплитуды называют десинхронизацией.

В настоящее время приняты два способа регистрации ЭЭГ – монополярный и биполярный. При монополярном отведении разность потенциалов измеряют между двумя электрически активными участками головного мозга (оба электрода находятся на коже головы) (рис. 1).

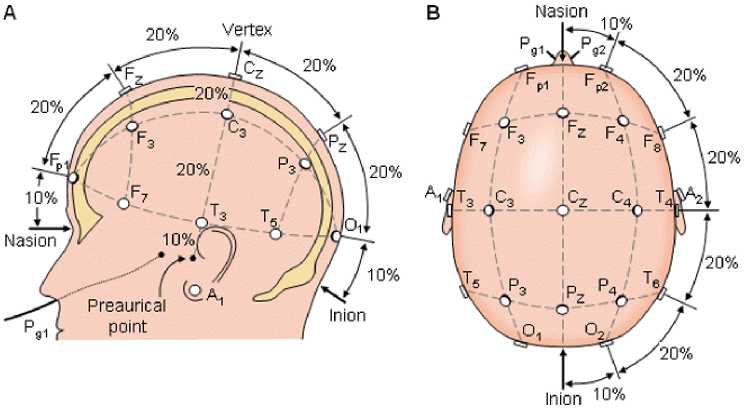
Рис. 1. Схема монтажа электродов электроосциллографа

Fig. 1. Scheme of installation of electrodes of an elektro-oscilloscope

Данная система позволяет построить координатную сетку, в узлы которой ставят электроды, получающие буквенно-цифровое обозначение по участкам: лобные, центральные, теменные, височные, затылочные. Всего устанавливается 19 датчиков, суммарная ЭЭГ по которым представлена на рис. 2.

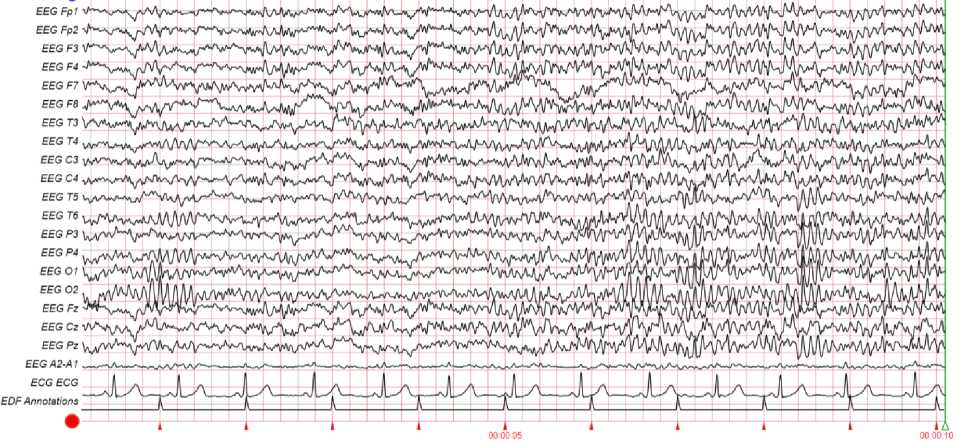
Рис. 2. Суммарная ЭЭГ по 19 датчикам

Fig. 2. Total EEG on 19 sensors

В ходе анализа были определены правила выделения ритмов вызванной [4, 5]:

• –    синхронизации: это альфа-ритм, определяемый на теменной и затылочной областях головного мозга датчиками: P 3, Pz , P 4, O 1, O 2 при амплитуде колебаний 40–80 мкВ и частоте 7,5–25 Гц ;

• –    десинхронизации: бета-ритм, определяемый на лобной и височной частях головного мозга датчиками: Fp 1, Fp 2, F 7, F 3, F 2, F 4, F 8, T 3, T 4, T 5, T 6 при амплитуде колебаний менее 15 мкВ и частоте 14–35 Гц .

С помощью такого подхода, как бинарные отношения характерности значений признаков для различных свойств и их сочетаний (г ^ , т = 1, М , I = 1,L), можно построить отношения доминирования по характеристике каждого свойства на множестве состояний объекта исследования [6]:

R^l = {(a_s, a_l) E A x A\Vm = 1,M (a_tm, a_sm) E r ^ и 3m₀ (I 0< M) такое, что

C^a sm_o , ^a lm_o ) ^{E r} m_o ^}, ^ = 1,^-

По сути, можно допустить вероятность того, что состояние, описываемое набором значений признаков и их сочетаний, не менее характерно для данного свойства объекта, также может быть определено экспертом, как его состояние:

если a_s E K_l и (a_t, a_s) E R^l , то a_t E K_l .                                                         (1)

Также можно сделать вывод о том, что если в некоторый момент времени объект исследования не обладает какой-то характеристикой, то это свойство не будет иметь место и в менее характерном для него состоянии:

если a_sE K_l и (a_s, a t ) E R^l , то a_t E K_l .                                                         (2)

При выполнении условий (1) и (2) можно сделать вывод о наличии свойств в ряде состояний, не проходя непосредственно идентификации с экспертом. Это даёт возможность организовать эффективную процедуру экспертного опроса, цель которого состоит в том, чтобы классифицировать все возможные состояния при уменьшении количества вопросов к эксперту [7].

Обработка экспертной информации

Мы обозначим множество номеров формируемых классов К = {0,1, ...,£}. Мы можем представить состояние а ^ E A в виде двух множеств: С * - множество номеров классов, которые соответствуют данному состоянию а ^ и С — — множество номеров классов, к которым состояние а ^ не может быть отнесено (будем называть такие классы невозможными).

Полагаем, что a i будет признано классифицированным, если

• С * П C i~ = 0, a C i* и C i- = K.                                                               (3)

Обозначим через подмножество состояний A⁰ с A, те, которые имеют классификацию [8]. В начале проведения экспертного опроса Vai E A, мы полагаем, Ci* = 0, С - = 0, A⁰ = A. Когда заканчивается процесс проведения экспертного опроса, то A⁰ = A.

Специальным образом в ходе экспертного опроса выбирается очередное состояние, которое будет предложено эксперту a i E A. Согласно заключению эксперта, состояние объекта имеет свой класс принадлежности, который представлен в виде перечня его номеров [9].

Таким образом, в состоянии a i очевидным способом определяется множество С * , а неявным - С^- = ^С * .

Далее состояние a i классифицируется и получает информацию, которая помогает уменьшить неопределенность в отношении других состояний A⁰ = A⁰ и a i .

Для каждого I E С * будет определено отдельное подмножество A * = {a j E A\(a j ,a i ) E R^l}, которое мы для него установим.

Начиная с каждого a j E A * мы должны определить С* = С * и I его отдельное множество:

A- = {aj E A\(ai, aj) E Rl} и для каждого aj E A— положим С^ = С- и I.

Для того чтобы показать работу алгоритма, можно воспользоваться ориентированными графами L , которые соответствуют бинарным отношениям доминирования, установленным по характеристикам: орграф G^l = {A,R^l} состояния из множества A , которые входят в состав орграфа, имеют свои вершины и дуги. Они объединяют их в качестве вершин и образуют отношения R¹ между ними [10]. Эти отношения имеют направление от состояний P l , которые являются более характерными для данного свойства, к менее характерным. (Обратим внимание, что все орграфы G^l , I = 1,Ь имеют одинаковое количество вершин).

На рис. 3 показаны два орграфа G¹ и G² для двух характеристик Р_± и Р₂. В данном случае состояние характеризуется значениями двух признаков Q₁ и Q₂.

В таблице содержатся номера значений признаков Q₁ и Q₂ в каждом из упорядочений по характерности для свойств Р₁ и Р₂, определяемых отношениями r¹, r², r₂ и r₂².

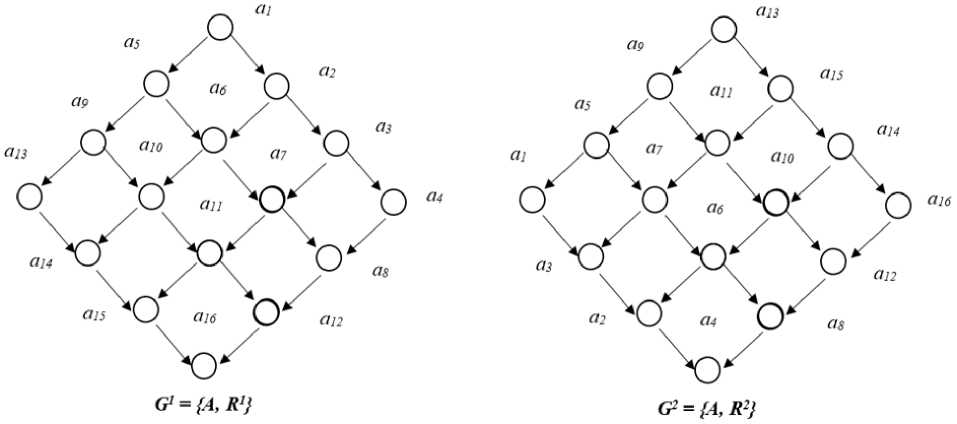
Рис. 3. Два орграфа G¹ и G² для двух характеристик P ₁ и Р ₂

Fig. 3. Two Artaud of columns of G¹ and G² for two characteristics of P ₁ and P ₂

Номера значений признаков Q ₁ и Q ₂

Numbers of values of signs Q ₁ and Q ₂

Значения признака Q1	У п оряд оченн ая по харак т ерн ос ти для с в ой с тв		Значения признака Q2	Упорядоченная по характерности для свойств
	P 1	P 2		P 1	P 2
Q ii	1	4	Q21	1	1
Q12	2	3	Q22	2	2
Q is	3	2	Qss	3	3
Q14	4	1	Q44	4	4

П уст ь на оч ер едно м шаг е экспер т у пр едъ я вля ет с я с о с т о я ние a₆ и он определяет, что С * = {1} и соответственно С ^ = {0,2}.

С форми ру е м мн оже с тв о с ос тоян и й А * ₁ = [a j 6 A\(a j , a₆) 6 Я¹}, из рис. 1 видно, что А₆ = = ^{ a i ,a₂,a₅ ^} .

Из условия (1) с лед у е т, что С * = С * = С * = {1}.

Сформируем множество А ₈₂ = {a j 6 A\(a₆, a j ) 6 Я²}: А₈₂ = {a₂,a₄, a₈}.

Из условия (2) с лед у е т, что С₄ " = С₈ " = {2}; а С₂ " = {0,2} и т. д.

В с е, о че м гов ори ло с ь р а нее, относится к решению задачи покрытия мн о же с тв а с ос тоян ий различными классами К₀,К₁, . ,К_Ь. Для того чтобы построить разбиение множеств A на классы К₀,К₁, ..,К_Ь , н еоб хо д и мо п ровести некоторые изменения в процедуре обра б отк и э к сп е ртн ой и нф орм аци и [1 1] . Т ак же и в общем случае, после того как эксперт класси фи ц и ров а л оче р е д н о е п ред ъяв ляе мо е е му с ос то ян и е a ^ 6 А, можно предположить, что все эти состояния (a j , a ^ ) 6 R^l тож е и мею т отн оше н и е к к ла сс у К_г. т. е. С* = {/}. При этом все эти состояния Р₍ можно отнести к клас с и фи ц и р ованн ы м , так к ак они не обладают никакими другими хар ак те ри с ти ка ми к ром е того, что и м п ри с у щ е . В св язи с этим операция определения невозможных к ла с с ов д ля ряда и ны х сос тоян ий долж на п рово д и ться, опираясь на информацию обо всех состоян и ях, к отор ые непосре д с тв е н н о и ли к о с в е н но к лас с и фи ц и р ов а н ы н а да н н ом э тапе.

Из условия (2) след у е т, что д ля к ажд о го a j 6 А * U a ^ для всех a_s 6 А^(£ ^ /) надо положить С ~ = С7 U t.

Проц е дуру н а зн а чени я н е в озможных классов для всех таких состояний a_s можно сделать бол е е эфф е к ти в н ой , е с ли для к аждого с в ой с тв а P_t (t ^ Z) выделить на подмножестве А * U a ^ подмн ожес тв о П аре т о п о отноше н и ю R^t (т. е. подмножество ^ j _t состояний, недоминируемых [12, 13]

по отношению R¹- ) и для каждого состояния a_s 6 А, для которого За ] 6 Пц такое, что (ар а^ ER¹, положить C i = C i U t.

Для начала рассмотрим вопрос о том, какова степень проявления свойств у состояний, которые входят в один и тот же класс. Степени проявления свойств Pi могут быть определены с помощью значений {P ^ ,P_i², ...,Р^ }.

Также эти значения можно обозначить с помощью естественного языка, например: «сильная», «средняя» и «слабая» степени. Определить необходимо, какие именно степени выраженности состояний характерны для классов K i .

В данной статье аналогичная задача классификации по порядку была рассмотрена в [12, 13]. На множестве {Р^Р?, ..^Р™ } было определено отношение линейного порядка R*, которое соответствовало тому, что (Pj^Pi') 6 R*, в случае если i < j. Благодаря использованию отношения г ^ (т = 1,М) которое характеризует значение каждого признака P i для свойства и бинарного отношения R¹ доминирования по характеристике данного свойства, можно уменьшить количество вопросов к эксперту в данной задаче. Каким образом, в случае если эксперт определяет для состояния a i 6 K степень P i и делает вывод о том, что состояние Ча ] 6 K i характеризуется степенью проявления свойств (а ^ , а ] ) 6 R¹ , становится известно, что степень проявления свойства P i не может быть больше, чем P i .

Если рассматривать все рассмотренные случаи, следует помнить о том, что множество состояний A может быть определено с помощью формального способа как декартово произведение шкал признаков. Находящиеся в нем состояния могут быть описаны различными значениями признака, которые противоречат друг другу. Предложенная процедура предполагает использование возможности ответа «состояние противоречиво» с указанием номеров значений признаков, которые не могут быть совмещены в реальной ситуации. В результате этого стало возможным исключить из множества все состояния, в описании которых присутствует указанная экспертом неоднозначная комбинация признаков [13].

Выявление ошибок в ответах эксперта и процедуры их устранения

Экспертный опрос, проводимый в целях выявления причин ошибочных ответов, должен учитывать возможность возникновения таких ситуаций. Это может быть вызвано усталостью эксперта или его недостаточной последовательностью при оценке сложных состояний, а также несоответствием модели (отношений г ^ , (т = 1, М; I = 1, L)) к реальной ситуации, которая имеет место быть.

Определение. Мы можем назвать ошибкой в построенной классификации состояний допущение нарушения условия (1) (т. е. такую ситуацию, когда состояние с более значимыми для данного качества характеристиками не относится к данному классу, в то время как к данному классу отнесено состояние, описываемое менее значимыми для этого класса характеристиками).

В [14] рассматривается ситуация, когда анализ и устранение ошибок при решении задачи о порядке проведения операций над множеством производится после классификации всех состояний исходного множества. С помощью диалогового решения задачи экспертной классификации появилась возможность проводить оперативную проверку создаваемой классификации на наличие в ней ошибок, которые могут быть обнаружены экспертом.

Для того чтобы построить покрытие множеств А, на следующем этапе экспертного опроса уже проведена классификация некоторых состояний, которые объединены в множество А⁰, и эксперту предоставляется для идентификации новое состояние а 1 . Если в результате проведения процедуры, описанной в предыдущем разделе, удалось определить множество классов А⁰ принадлежности C i и C i - множество номеров невозможных классов для состояний, то можно предположить, что это произошло благодаря косвенному определению множества номеров классов принадлежности и множеству номеров невозможных типов состояний а 1 . В момент непосредственного определения состояния эксперт явно указывает на наличие множеств классов принадлежности C i и их номера, а также косвенные номера невозможных классов C i .

Утверждение . Если задача покрытия имеет целью обеспечить отсутствие ошибок в классификации состояний А⁰ = А⁰ U а 1 , то необходимо выполнить следующие условия:

C i с C i , С Ц с C i . (4)

Доказательство. Пусть при выполнении соотношений (4) в построенной классификации имеются ошибки. Тогда в силу определения ошибок Ba j , a i и K i такие, что либо

• (a ; , aj} 6 Л¹, a j 6 K i и a ; 6 K i ,

либо

• (a j , a;} 6 Rⁱ, a j ^E K i и a ; 6 K i .

Так как a j 6 K_i , a (a ; , aj} 6 R^l, то I 6 С * . Но по условию a ; Е K_i , т. е. 16 С * , следовательно, С * с С * . Аналогично во втором случае имеет место соотношение С - с С - , а это противоречит сделанным предположениям. Тем самым доказана достаточность утверждения. Заметим, что для задачи разбиения в силу того, что |С * | = \С * \ = 1, необходимо и достаточно выполнение соотношения С - С С - .

Ошибки в построенной классификации состояний могут быть следствием как ошибок эксперта, который определяет классы принадлежности для каждого состояния, a ; , так и ошибок, которые возникают при классификации некоторых состояний А⁰, которые имеют с состоянием нарушение условия (1). Опишем через некоторое количество способов множество подобных состояний А_егг . Для исправления ошибок необходимо повторно представить эксперту состояние a ; и a j 6 А_егг , для того чтобы он смог более подробно рассмотреть их. Ошибочность модели, которую разработал эксперт, и необходимость ее пересмотра может быть подтверждена отказом эксперта изменять данные им ранее ответы. В случае, когда происходит повторное рассмотрение состояний a ; и a j 6 А_егг и эксперт дает новый ответ по поводу состояния, процесс обработки этого ответа будет осуществляться заново. В соответствии с процедурой, описанной в предыдущем разделе, это происходит в порядке, аналогичном тому, как это описано в предыдущих разделах. В случае, если эксперт признает свою ошибку при классификации состояний А_егг , он должен будет внести изменения в их классификацию [15].

Обозначим следующим образом алгоритм внесения исправлений в ошибочную классификацию:

• -    S * - классификация состояний из-за неправильного определения классов принадлежности приводит к множеству номеров, которые не соответствуют друг другу. А⁰: S * = С * \(С * П С * };

• -    S ^ - среди множества номеров классов, которые были ошибочно исключены из числа возможных для определенного состояния в результате классификации состояний из множества других факторов, есть некоторое количество классов, которые не подходят для данного состояния. А⁰: S ;- = С Г \(СГ П С-}.

Для задачи покрытия алгоритм будет иметь следующий вид:

Шаг 1 . Для каждого l 6 S * сформируем подмножество А е _гг с А_егг такое, что А е _гг = = {a j 6 А_еrr\(a i , aj} 6 R^l, a j 6 K_i} и Va j 6 А¹_егг , полагаем С * = С*\1.

Шаг 2. Для каждого l 6 S - сформируем подмножество А е _гг с А_егг такое, что А е _гг = = {a j 6 А_еrr\(a j , a;} 6 R^l, a j E K_i} и Va. j 6 А¹_егг , полагаем С * = С+\1.

В алгоритме используется диалоговый режим, в котором все изменения, внесенные в классификацию, должны быть согласованы с экспертом.

Исправление ошибок, допущенных в классификации состояний А⁰, невозможно осуществить в единственном экземпляре для каждого класса, так как не существует способа проведения необходимых изменений в каждой категории ранее определенных состояний. Данный случай предполагает, что каждому из состояний должен быть назначен только один класс принадлежности. В этом случае возможно (в процессе исправления ошибки) добавление дополнительного класса принадлежности к некоторым из этих состояний, что приводит к необходимости исключить ранее назначенные им классы принадлежности А⁰ . Следовательно, это может привести к исключению классов принадлежности у некоторых других состояний, в результате чего они снова станут неклассифицированными.

Алгоритм коррекции в задаче разбиения имеет следующий вид:

Шаг 1 . Пусть a ; 6 K_i :

Шаг 2 . Сформируем множество А_егг = {a j 6 А⁰\(a j , a;} 6 R^l, a j E K t }.

Шаг 3 . Vaj 6 А_еггVt * l (t = 1,L) сформируем множества:

А ^гт = {a_q 6 А⁰\(a j ,a_q} 6 R^l и a_q6 K_i}.

Шаг 4 . Va_a 6 А^ положим С * V 0 и А⁰ = А⁰\a_o.

Ч CII                 Ч                         Т

Выводы

Для проведения опроса специалиста, исследующего ЭЭГ, изначально было сформировано все многообразие возможных состояний, которые описываются значениями признаков. В общей сложности, количество подобных состояний равно 216. Когда происходил диалог, специалист получал на естественном языке изложение своего состояния, являющееся своеобразным фрагментом истории болезни пациента. На экране дисплея было представлено «меню» возможных ответов, включающее в себя: 1 – синхронизация, 2 – десинхронизация, 3 – состояние покоя, 4 – ни одно из заболеваний, перечисленных ранее, 100 – ситуация неоднозначна. После получения заключения эксперта ему было предложено оценить степень вероятности наличия заболевания или его симптомов в данном состоянии, используя термины «сильная», «средняя» и «слабая» степени вероятности. Для врача это означало, что перед ним стояла стандартная задача по постановке диагноза. В результате использования рациональной процедуры опроса, в ходе которой было представлено наиболее информативное состояние, удалось за короткий период времени провести классификацию возможных состояний и получить ответы на все вопросы. Всего было задано около 40 вопросов. С помощью системы результаты классификации были сведены в единую базу знаний, которая включала в себя номера состояний, классы принадлежности (диагнозы) и номера степени вероятности для каждого из них. Такое представление знаний имеет место быть потому, что каждое состояние может быть описано набором признаков, которые имеют однозначное соответствие его номеру. Таким образом, благодаря использованию такой организации данных в базе знаний системы можно вычислить номер из базы знаний по совокупности симптомов пациента и определить его диагноз.

Для того чтобы получить от экспертов исчерпывающую и непротиворечивую совокупность правил, которые будут основаны на простых и понятных действиях, необходимо применить предложенный подход к решению задачи экспертной классификации. В диагностической системе полученные знания легко объединяются в базу знаний, которая экономит ресурсы памяти и быстро находит решение проблемы. Несомненно то, что приобретенные классификации могут быть представлены в традиционной для экспертных систем форме продуктов. Как показал опыт использования диагностической системы, предлагаемый нами способ организации данных имеет более высокую эффективность в сравнении с традиционным.