Амплитуда рассеяния упругого шарика в вязкой изотропной жидкости

В идеальной жидкой среде задача расчета радиационного давления (рд) сводится к решению линейной задачи рассеяния на включении. Случай включений с потерями в идеальной жидкой среде сводится также к решению такой же задачи рассеяния (см., например, [1]). Однако, как известно, отсутствие учета вязкости внешней среды может приводить к сильному искажению реальных значений рд вследствие возникновения пограничного слоя вокруг включения даже при небольшой вязкости. Общие методы расчета рд при учете вязкости достаточно трудоемки. Следующим по сложности после идеальной жидкости является случай маловязких окружающих жидкостей. При больших числах Рейнольдса R , соответствующих малой вязкости, жидкость может рассматриваться как идеальная, но только вне пограничного слоя вокруг твердого включения [2]. Тогда задача расчета радиационного давления на одиночном включении сводится к случаю идеальной жидкости при условии того, что в качестве включения выступает совокупный объем, состоящий из реального твердого включения и прилегающего к нему пограничного слоя. Эта идея не является оригинальной. Она высказывалась еще в работе [3], а в работе [4] она реализована точно в такой же постановке, как и в работе [5], только с добавлением пограничного слоя. При этом авторы [4], как и в [5], получают частное решение, ограничиваясь при описании включения мультиполями только нулевого и первого порядка. Вместе с тем в идеальной жидкости эта теория распространена на включения с произвольной амплитудой рассеяния (ар) (см., напри- мер, работы [6–8]). Необходимость этого видна хотя бы из работы [1], когда нужно учитывать произвольное количество мультиполей.

Как известно, в идеальной жидкости при расчете рд достаточно вычислять ар включения в линейном приближении [5]. Тогда при работе с маловязкими жидкостями, когда вне пограничного слоя жидкость можно считать идеальной вне пограничного слоя, очевидно так же, что для расчета рд достаточно вычислить ар в линейном приближении. Поскольку вязкая жидкость описывается нелинейным уравнением Навье—Стокса, необходима его линеаризация с последующим вычислением ар в линейном приближении. Поскольку эта процедура расчета ар не связана с величиной вязкости жидкости, то она будет универсальной вне зависимости от величины вязкости.

В литературе есть примеры расчетов ар включений, находящихся в вязкой среде. Так, в работе [9] вычисляется ар бесконечного полого цилиндра, покрытого вязкоупругой оболочкой, находящегося в идеальной жидкости. Оболочку в известном смысле можно интерпретировать как пограничный слой. В работе [10] рассчитывается ар заполненной водой полой сферы, находящейся в вязкоупругом однородном пространстве. В отличие от [9, 10], где учитываются причины затухания звука связанные только с вязкостью, в работе [11] рассчитывается ар на упругом шарике с учетом только тепловых эффектов как в окружающей среде, так и в шарике. Здесь следует отметить похожесть молекулярного механизма поглощения звука как под влиянием вязкости, так и под влиянием теплопроводности, что проявляется в симметричной зависимости коэффициента поглощения от коэффи- циентов, характеризующих оба этих эффекта [2, выражение (79.6)].

в случае учета тепловых эффектов — так [14, с. 13]:

ПОСТАНОВКА ПРОБЛЕМЫ

p = c ² p — к

f 1

—K- v .

В настоящей работе рассматривается простейшая осесимметричная задача рассеяния: на упругий шарик радиусом a , помещенный в вязкую однородную жидкость, падает плоская потенциальная волна, распространяющаяся вдоль положительного направления оси Oz . Центр шарика помещен в начало координат О .

Пусть жидкость и упругое включение характеризуются следующими константами соответственно: параметрами Ламе λ , µ и λ ₁ , µ ₁ ; скоростями звука c в жидкости, и продольной

I c v

p 7

(3а)

c =

Л 1 + 2p_x

ρ 1

µ

, и поперечной c ₂ = — ρ ₁

в упругом

Здесь κ — коэффициент теплопроводности; c_v , c_p — удельные теплоемкости при постоянном объеме и давлении соответственно.

Ввиду малости коэффициента теплопроводности κ в жидкостях и газах вторым членом в (3а) часто пренебрегают [15, с. 22]. Это приводит уравнение состояния (3а) к (3). Поэтому в настоящей работе примем уравнение состояния в виде (3).

Из уравнений (1), (1а) видно, что выполняются соотношения между коэффициентами динамической вязкости λ , µ и коэффициентами η , ς

шарике.

Примем, что v ₀ , p ₀ , ρ ₀ значения скорости, давления

— невозмущенные и плотности жидко-

n = p , q = X + 3 p.

сти; v , p , ρ — возмущения этих значений вследствие колебаний жидкости. Примем, что жидкость является вязкой, сжимаемой и изначаль но неподвижной v ₀ = 0 . Плотность шарика — р 1 . Суммарное давление p ' и плотность ρ ' в жидкости тогда равны p ' = p + p 0 , p = p + p ₀.

При принятых допущениях движение изотропной вязкой жидкости описывается системой уравнений Навье—Стокса, в которую входят:

– собственно уравнение движения Навье— Стокса либо в терминах коэффициентов динамической вязкости λ и µ , являющихся соответственно первым и вторым параметрами Ламе [13, с. 206]

РЕШЕНИЕ ПРОБЛЕМЫ

Для решения линейной задачи рассеяния необходима линеаризация системы уравнений Навье— Стокса (1), (2). Линеаризованная версия уравнения (1) имеет вид (см., например,[14–19], для (1а) — то же, просто необходимо учесть соотношение между постоянными (4))

p 'l — + ( v -V ) v l = -V P '+ p A v + ( X + p ) VV- v ,   (1)

d v     1 X + p^^

— =--Vp +---— VV - v + vAv,(5)

5 t    po а уравнение неразрывности (2) [2, с. 350]:

^p + poV-v = 0.(6)

d t

Далее принимается стандартное представление

либо в терминах коэффициентов η сдвиговой и ς объемной (второй) вязкости [2, с. 73]

v = v i +v t, vl = VФ,  v t = Vx T,

V Y = 0,

p 'l — + ( v -V ) v I = -V p '+ n A v +

– уравнение неразрывности [2, с. 15]

^p + V- ( p v ) = ^p + p V- v + v -V p = 0; d t       ^v         d t

где Ф — скалярный, а Y — векторный потенциалы вектора колебательной скорости. После несложных преобразований из (5)–(7) получены следующие соотношения [14–19]:

—Ф — c ² 1 +

d t ²

k

X + 2 p d ------- 1АФ, p0 c2 dt J

– уравнение состояния, замыкающее систему; в случае баротропной жидкости записывается так [2, с. 351]:

—T = ^p A Y , d t

ρ ₀

p ' = f ( p ') или    p = c ² p ,                (3)

d ²

v dt2

l

—

c ² 1 + k

X + 2 p dL _n

I A v _l = 0, p ₀ c ² d t J

д vt д t

p =

—

^— — A v t = °,

ρ ₀

д .                x „

" P o - Ф' ( X + 2 Ц ) АФ , д t

P 5^ (X + 2ц) p - — ' 0—ф . '---- ЛФ .

c ² д t         c ²

Здесь A — оператор Лапласа, который в случае осевой симметрии равен л 1 д 2 д

A =-- r ² — + r ² д r    д r

1 д . _ д sin θ .

r ² sin в д в      д в

Рассмотрим стационарный гармонический процесс с временным фактором e ^{— i — t} . Тогда для амплитуд вышеприведенных соотношений имеем (для удобства амплитуды обозначены теми же символами)

2 АФ + — 2 c	1 — i—X + 2— P0 c 2 J	- 1 Ф- 0,	(8)
А Т + i—	p 0 T - 0, µ		(9)
ω 2 A v i + — c 2	1 — i—X + 2— I        P 0 c c	X — 1 v I - 0,	(10)
µ — i— v t - — A v t ρ 0 p - i—p0 Ф + ( X + 2 ц ) AФ ,			(11) (12)
P - i—p0 c 2	( X . 2 ц ) Ф + Ф---— AФ . c 2		(13)

Задачам (8) и (10) соответствует комплексное волновое число

ω ki =-c

(

1 — I®

\ —1/2

X + 2 ц ]

I

P o c ² J

— С . X + 2ц) — 1 + ito- | = c I      2 Po c2 J

= k _z'+ ik ",     k _z' = ^— ,       k _z" = ® ^{2 X +} 2^— ,

/              / *                  I                  *                       IЛ *

c2

где приближение (14), очевидно, справедливо при условии

^{— ( X +} 2 — ) _D 1 c ² ρ ₀

что физически всегда выполняется в случае, когда амплитуда волнового процесса на расстояниях порядка длины волны изменяется слабо [19, с. 23].

Задачам (9) и (11) соответствует комплексное волновое число k-(i + 1) I V -

- k, '+ ik_t ",      k_t' - k_t " = . — , v = ^— .         (15)

^{t t t t}       2 ν         ρ ₀

В работах [16, 17] и других публикациях автора этих работ показано, что решение задачи (7), в частности, в сферических координатах ( r,6,ф ) можно искать через три разделяющихся по уравнениям и краевым условиям скалярных потенциала Ф , ф₁ и ф ₂:

v = VФ + Vx г ф₁ + VxVx г ф ₂.         (16)

В случае осевой симметрии, когда отсутствует зависимость решения от угла азимута ϕ , потенциал ψ ₁ равен нулю и последнее выражение принимает вид [20]

v = VФ + VxVx г ф ₂.            (17)

Здесь Ф удовлетворяет уравнению (8), а ф ₂ — уравнению типа (9)

— i—ф ₂ - ^— А ф ₂.               (18)

ρ ₀

Разложим осесимметричные потенциалы по полиномам Лежандра. Для жидкости имеем:

Ф _i - e r ■■ - e^ik i r ^{cos 6} - £ (2 n + 1) iⁿj_n ( k_lr ) P_n (cos 6 ) (19) n - 0

— для падающей волны и ro

Ф , - ^ A n (2 n + 1) i n h n •( kr ) P n (cos 6 )            (20)

n - 0

— для потенциальной части рассеянной волны (jn, hn1 — сферические функции Бесселя). Для соленоидальной составляющей рассеянной волны ro ф2 -^Bn(2n +1)inhn’(kr)Pn(cos6).           (21)

n - 0

Скалярный и векторный потенциалы в упругом шарике имеют вид [9]:

ro

Ф ⁽¹⁾ - ^ C n (2 n + 1) i n j n ( k 1 r ) P n (cos 6 ),          (22)

n-0 ro ф2(1) -^Dn(2n +1)injn(k2r)Pn(cos6),         (23)

n - 0

ω где k.  --волновые числа продольных i -1 и ci поперечных i - 2 волн в шарике; An, Bn, Cn, Dn — искомые постоянные. Потенциалы Ф(1) и ф2(1) удовлетворяют следующему уравнению Гельм- гольца [9]:

-1 |f r 2 . ^Ф I T r ² д r к д r k w ₂ ⁽¹⁾ ))

+

1 д r ² sin 0 д 0

_f д fФ ⁽¹⁾

sin 0—  „

к

9 0 k w ₂ ⁽¹⁾

f k'

к k 2

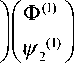
= 0.

Выражение для ар f (θ) получается из (20) (потенциал (21) участия в формировании ар не принимает вследствие его быстрого затухания) подстановкой асимптотики функции Ханкеля hn'(z) 0 — i~n—1 eiz при z ^да и вычленением мно-z eiklr жителя . Имеем окончательно r

покоящейся вязкой жидкости, а в работах [23, 24] — для смещений и напряжений однородного упругого тела через соответствующие скалярные потенциалы. Поскольку результаты в [23] и [24] для случая упругого тела отличаются, автором в работе [9] соответствующие выкладки были перепроверены, и результаты совпали с результатами работы [23]. Формализму постановки задачи в настоящей работе соответствуют выражения, полученные в [22], однако во избежание ошибок полученные там выражения также были перепроверены. Детали вычислений изложены в Приложении. Результатом являются формулы:

д f .   1 д 2 д к vr =—Ф-| rA---r2— w 2 = дr    к r д r   дr )

”

f (0 ) = — Z A n (2 n + 1) P n (cos 0 ). (24) ik l n = 0

Таким образом, для вычисления ар f ( θ ) необходимо знать коэффициенты A_n . Это достигается в общем виде путем вычисления всех коэффициентов A_n , B_n , C_n , D_n при удовлетворении краевых условий на поверхности шарика.

В случае, когда упругий шарик находится в вязкой жидкости, на границе раздела между ними должны быть непрерывны векторы скорости и попарно нормальные и касательные компоненты тензоров напряжений в шарике и в жидкости [21]. С учетом осевой симметрии задачи это означает:

– радиальная компонента скорости в жидкости vir + vsr и в упругом теле v(1)r на поверхности шара равны vir + vJ = v (1l| ; (25) ir sr ir=a r |r=a ’ v /

д f , „ д      д ² к

=—Ф + | rk2 + 2--+ r---w 2, дr     к         д r    д r2 )

1 д      1 д д ²

v0 =--Ф +--W 2 +-----V 2, r д0    r д0     дrд0

—i

bk. = + ^д 1ф+

9 r r

(          9     92     93 \

+| к ² + к ² r —+3 —+ r —W f= к ‘     ‘ д r     д r ²     д r ³ Г ²

= 2 ^ \ k_t ²

—

ipro  д² V

°-S— + — |Ф+

2 ^   д r ²)

f „      „ д     д ²       д ³ к    I

+| к , ² + kt² r — + 3— + r— w ₂ f , к д r     д r ²     д r ³ )   I

σ rθ

Ф +

– полярная компонента скорости в жидкости v_{i 0} + v_{s 0} и в упругом теле v ⁽¹⁾ ₀ на поверхности шара равны

д f д ²     1 д

+1

д 0 к д r ² r д r

—

11 — + ~k, r ²    2 ^t

V 2 .

v 0 ⁺ v s0 | r = a = v ⁽¹⁾ 0 L = a ;

– равны попарно одноименные компоненты тензоров напряжений, отличных от нуля:

^ = a = ^ r ⁽¹⁾ I r = a ,                     ⁽²⁷⁾

^ r0 I r = a = ^ r0 ^(1> I r = a "                     ⁽²⁸⁾

Здесь b = —. Выражения (29)-(32) совпали с вы-2µ ражениями (3.4), (3.5) работы [22].

Выпишем в парциальном виде условие (25). Для этого вначале перепишем оператор в (29), воздействующий на ψ ₂ в следующем виде:

Здесь верхний индекс ⁽¹⁾ указывает принадлежность к шарику; азимутальные компоненты скоростей и касательных напряжений на поверхности шарика в силу осевой симметрии равны нулю.

В работах [21, 22] приведены выражения для компонент скорости и напряжений для изотропной

1д д rA---r2 — = r д r   д r

1 д д 1 д д

=--r2--1---sin 0— r дr  дr  r sin 0 д0     д0

1 д

r sin 0 д 0

■ о д sin θ .

д 0

—

1 д д r ²

r д r   д r

Далее, учитывая уравнение для полиномов Лежандра, получаем

1 d ( . d         a

———I sin ^e— P n (cose ) | = - n ( n + 1) P n (cose )• sin e d e v s o          j

Тогда воздействие упомянутого оператора на парциальный полином Лежандра приводит к следующему равенству

1 5,5V,        1

r A--- r ² — | P n (cos 0 ) = — n ( n + 1) P n (cos 0 ).

r d r    d r J              r

С учетом всего перечисленного из условия (25) в парциальном виде получаем следующее равенство

xh n ' ⁽ x ) A n ^{+ n ( n +} 1) h n ⁽ x ) B n ^{+ i to x} x j_n ' ⁽ x ) ^C n ⁺

⁺ iron ⁽ n + 1) j_n ⁽ x 2 ) D n = ^- xj_n ' ⁽ x i ).                 (33)

Здесь x_i = k_ia , x_t = ka , x 1 = k 1 a , x ₂ = k ₂ a ; штрих означает дифференцирование по аргументу функции.

Рассмотрим условие (26). Здесь, учитывая выражение (30), для полярной составляющей скорости необходимо воспользоваться равенством

—— P (cos0) = P 1(cos0). Тогда условие (26) в dθ n          n парциальном виде можно записать так hn (xi ) An +( hn (xt) + xhn '(xt ) ) Bn + irojn (x1) Cn +

^{+ i ro} ( ^jn ⁽ x 2 ) ⁺ x 2 ^jn ' ⁽ x 2 ) ) D n = - ^jn ⁽ x i ).              (34)

Далее рассмотрим условие (27). Выпишем в парциальном виде σ_r , следуя (31), и σ_r ⁽¹⁾ , следуя выражению (18) работы [9] с учетом обозначений настоящей работы. Для σ_r :

² T I k i

V ^V

—

j

PH j n ( kr ) + ki² j n "( kr ) +

2ц J                J

+ 2ц | k i ²

—

A" | h n ( ka ) + k i² h n ''( ka ) | A n +

2ц J                  J

+2 ^ ^k t ² ( h n ^{( k} t r ) ⁺ x t h n ' ^{( k} t r ) ^{+ 3} h n "^{( k} t r ) ⁺ xh n "'^{( k} t r ) ) B n ;

для σ_r ⁽¹⁾ :

2 µ (1) k ₁ 2

σ

—

V (1 - 2c )

jn ( X 1 ) + j_n "( X 1 ) | C n +

^{+ 2} Т ^{(1) k} 2 ² ( ^j _n ^{( x} 2 ) ⁺ x 2 ^j _n ' ⁽ x 2 ) ^{+ 3 j}n "( x 2 ) ⁺ x 2 ^jn '"( x 2 ) ) ^D n ^.

Здесь σ — коэффициент Пуассона материала шарика. Приравнивая эти выражения, получаем третье уравнение системы

j - ²

—

iP ⁰ ^ | h n ⁽ x i ) + k i² h n "⁽ x i ) | A n ⁺

2 ц J                J

^{+ k} t ² ( ^h n ⁽ x t ) ⁺ x t h n ' ⁽ x t ) ^{+ 3 h} n "⁽ x t ) ⁺ x t h n "'⁽ x t ) ) B n ^-

- w ( - b j n ( x ) + j n ■( x ) ) C n - ^^ _x

µµ

^x ( ^jn ^{( x} 2 ) ⁺ x 2 ^jn ' ^{( x} 2 ) ^{+ 3 j}n "( x 2 ) ^{+ x} 2 ^jn '"( x 2 ) ) ^D n =

= - ⁽ k i ² - iP^^ | j_n ( x - ) + k i² j n "( x - ) | .               (35)

Л 2 ^ц J              J

Здесь

σ

(1 - 2 c )

λ (1)

2 µ ⁽¹⁾

= b ⁽¹⁾ .

Далее найдем четвертое уравнение системы из условия (28). Напряжение σ_{r θ} (32) переписываем

в парциальном виде, учитывая равенство

- d, P_n (cos 0 ) = P_n ’(cos e ):

ОТ ( ( x i ^j n '⁽ x i ) - ^jn ⁽ x i ) ) ⁺ ( x i h n '⁽ x i ) - h n ⁽ x i ) ) A n ) ⁺

⁺ 2 r ( x t² h n "⁽ x t ) ⁺ x t h n '⁽ x t ) ^{+ ( 1} x t ^{2 - 1} | h n ⁽ x t ) | B n . a ² v                            V 2 J J

Напряжение σ_{r θ} ⁽¹⁾ с учетом принятых здесь обозначений получается из выражения (2.45') работы [23]:

2 µ (1)

( ( ^x 1 ^jn '^{( x} 1 ) ^{- j}n ^{( x} 1 ) ) C n ) ⁺

2ц ⁽¹⁾ ( , X              x ( 1   , z

⁺ ^^I ^x 2 Jn ⁽ x 2 ) ⁺ x 2 Jn ⁽ x 2 ) ⁺I - x 2 ^{- 1} | Jn ⁽ x 2 ) | ^D n ^.

a ² V                       V 2       J J

Два последних выражения с помощью уравнения для сферических функций Бесселя R_n ( kr )

_ d2          5     , _ _ r2--+ 2r--+ (k2r2 - n(n +1))

5 r ²       5 r   ^{( V V)}

R n ( kr ) = 0

приводятся соответственно к виду

'2Ц ( ² ( x i j n '⁽ x i ) ^{- j}n ⁽ x i ) ) ^{+ 2} ( x i h n '^{( x} i ) ^- h n ⁽ x i ) ) A n ) ⁺

+ 2P( xt2 hn "(xt ) + (n 2 + n - 2) hn (xt ) ) Bn , a2

2 Ц ^ (2 ( X 1 j n '( X 1 ) - j n ( X 1 ) ) C n ) +

⁺ 2 “ T- ( x 2 ^{2 j}n "⁽ x 2 ) ^{+ (} n ^{2 +} n ^{- 2) j}n ⁽ x 2 ) ) D n .

a ²

Условие (28) в парциальном виде запишется следующим образом:

2 ( xX '(xl) - hn (xl) ) An + a14 = iron (n +1) jn. (x 2).   a 24 = ito( jn (x 2) + x2 jn'(x 2)).

_µ (1) _k 2

^a 34 =-- ^µ

x

+ ( xt ² h n "( xt ) + ^{( n 2} + ^{n — 2)} h n ⁽ X ) ) B n

-

X ( j n. ^{( x} 2 ) + ^x 2 j_n '( ^x 2 ) + ³ j_n "( ^x 2 ) + ^x 2 j_n '"( ^x 2 ) ) .

— ^- 2 ( x , j ; '( x , ) — j ; ( x , ) ) C n ^µ

-

µ (1)

--( x 2 ² j "( x 2 ) + ⁽ И ² + И ^{— 2)} К ⁽ x 2 ) ) d . = ^µ

= - ² ( xj n '( x l ) - jn ⁽ x l ) ) .

Окончательно запишем систему (33)–(36) в виде

( a « ) . ( G j ) , = ( F ) . . ‘ , j = 1.4.

Здесь

µ (1)

^a 44 =-- ( x 22 ^jn "⁽ x 2 ) ^{+ (} n ^{2 +} n ^{— 2) j}n ⁽ x 2 ) ) •

µ

Для определения амплитуды рассеяния (24) необходимо отыскание лишь постоянных A_n , n = 0,1.2.... К сожалению. в описываемом четырехмерном случае в отличие от трехмерного, описанного в [9], не удалось получить компактное выражение для постоянных A_n . Однако не представляет проблем получение численных решений (37) для получения A_n в функции от волнового параметра x_l = k_la .

Г An )

⁽ G j ) ,

B n

C n

,

( F i ) n =

I D

—

n У

x_l j_n '( x_l )

^— К ⁽ xl )

—

I k ²

—

iρ ₀ ω

2 µ

\

\

^jn ⁽ x l ) + ki ^{2 j}n "( x l )

У

, ² ( x l j n ' ⁽ x l ) ^{— j}n ⁽ x l ) )

У

— вектор-столбцы искомого вектора части системы.

Для элементов матрицы ( a j ) имеем:

и правой

^а 11 = xK ' ⁽ x l ).   ^a 21 = h n ⁽ x l ).

^a 31 =f ^k l ² — i"^ ) ^h n ⁽ x l ) + ^k l^{2 h} n "⁽ x l X

V      2 И У

• ^a 41 = ² ( x l h n ' ⁽ x l ) ^— h n ⁽ x l ) ) .    ^a 12 = n ⁽ n + !) h n ⁽ x ).

• ^a 22 = ( h n ⁽ x ) + xh n ' ⁽ x ) ) .

• ^a 32 = kt ² ( h n ⁽ x ) + xh n ' ⁽ x ) + ³ h n "( x ) + xh n '"( x ) ) .

a 42 = X t ² h n "( X t ) + ( n ² + n — 2) h n ( x ).

• ^a 13 = itox 1 ^jn ' ^{( X} 1 ). ^a 23 = ito ^jn ^{( X} 1 ).

• ^a 33 = ^— B_k l_ ( ^— b ⁽¹⁾ j_n ⁽ x 1 ) + j_n "⁽ x 1 ) ) .

µ

µ (1)

a43 =--2 ( X1 jn '(X1) — jn (X1) ),

µ

ВЫВОДЫ

Таким образом, на основе линеаризации системы уравнений Навье—Стокса без учета тепловых эффектов получена СЛАУ четвертого порядка, позволяющая в конечном итоге вычислять амплитуду рассеяния однородного упругого шарика в вязкой жидкости в линейном приближении с произвольной точностью (до мультиполей произвольного порядка). Это в свою очередь позволит применить процедуру вычисления радиационного давления через амплитуду рассеяния в линейном приближении, разработанную ранее для идеальных жидкостей, и в случае слабовязких жидкостей. Описанная процедура получения амплитуды рассеяния в линейном приближении является универсальной и не зависит от величины вязкости жидкости.

Для символьных вычислений в работе использовался пакет Mathematica-8, лицензия L3259-7547.

ПРИЛОЖЕНИЕ

Как известно, определяющие уравнения, связывающие тензор напряжения с тензором скорости деформации для вязкой изотропной жидкости и с тензором деформации для изотропного упругого тела, весьма похожи. Для жидкости при небольших скоростях деформации имеем (см., например, [13, с. 199], [18, с. 350]):

Оу =(—p + ^V- v) 5j + 2 ^sj.

ε

ij 2

d V.    ^d v j

+ dx,    оx, ji

(П1)

Для упругого тела имеем (см., например, [18, с. 347], [25, с. 48]):

о„(1) = A(1)V- u(1)^ + 2 ц (1)8,(1), ij                                        ij                      ij m 1 Гдu (1) au(1)I

8 ⁽¹⁾ = -— + — j— .

ij     2 ax,      ax ji

Здесь σ_ij , σ_ij ⁽¹⁾ — тензоры напряжений; ε_ij — тензор скоростей деформаций в жидкости и ε_ij ⁽¹⁾ — тензор деформации в упругом теле (индекс ⁽¹⁾ относится к упругой среде); δ_ij — единичный тензор (дельта-символ Кронекера); v_i и u_i ⁽¹⁾ — соответствующие компоненты вектора скорости и с мещения в декартовой системе координат, i = 1,3 . Учитывая известные выражения для тензора деформации упругого тела ε ⁽¹⁾ в сферических координатах [18, с. 367] и его абсолютную схожесть с тензором скорости деформации ε с точностью до буквенных обозначений, можно для него воспользоваться теми же выражениями, поменяв u ⁽¹⁾ на v . Поэтому имеем для компонент тензора скоростей деформации, необходимых для решения проблемы в случае осевой симметрии:

д

⁸ r = 7 v r , д r

1 ( д

⁸ 9 =-| —^9 ⁺ v r r (д 9

⁸ _Ф = ¹ ( v 9 ctg ^{9 +} v r ) , r

⁸ r9 =

1 f д 1 f д

I — v ₉ +“I — v r 2 (д r    r (д 9

v _θ

Для нужных компонент тензора напряжений имеем из (П1):

^ r = - Р ⁺ ( ^ ⁺ 2 Ц ) ⁸ r ^{+ 2} ( ⁸ 9 ^{+ 8} Ф ) ,

^O r9 = ^{2 Ц8} г 9 .

Подставляя соответствующие выражения для компонент тензора скоростей деформации, имеем для компонент напряжения:

д

^ r = - Р ⁺ ( ^ ⁺ 2 Ц ) — v r ⁺ д r

„ 1 Кд I _{Л X}I

+ ^ |    v9 + vr l + (v9ctg9 + vr )l,(П2)

r \\д9      ))

f д     1 f дII

^r9 = ц| —v9+ |    vr — v9 ll .

(дr    r(д9

Выразим все величины через скалярные потенциалы. Из (17) получаем

—

д _ 1 1 д . А д v, =—Ф----sin 9 — дr    r sin 9 д9 д9

ψ ₂ .

Учитывая, что лапласиан в случае осевой симметрии равен

,    1 д 7 д 1 д . „ д

А =--r2--+--sin 9—, r2 дr   дr  r2 sin 9 д9     д9

а также тождество ( А + k_t ² ) ^ ₂ = 0, последнее выражение переписываем в виде (29). Для v _θ имеем (30). Для нормального напряжения (П2) воспользуемся связью давления с потенциалом (12) и тем, что АФ = — к, ² Ф ; получаем (31). Для касательного напряжения σ_{r θ} — (32).

Далее приведем необходимые выражения для упругого шарика [9, 23]

ur

д 11 д f _Q д _m

= —Ф⁽¹⁾---- 1 sin 9—w 2 ⁽¹⁾

д r      r sin 9 д 9 ( д 9

u 9 =

1 ±Ф (1)

r д 9

1 _д_ r д r

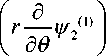
o r ⁽¹⁾ = 2 ц ⁽¹⁾

— b ⁽¹⁾ к ,² +— |Ф ⁽¹⁾ + ¹     д r ² J

+ | к. ² + к ² r — + 3— + r^д- I w ⁽¹⁾ I ^{2      2} д r      д r ²      д r ³ ) ²

О ⁽¹⁾ r9 = 2 ц ⁽¹⁾

" 1 д f д 1

1 |ф ⁽¹⁾ + r д 9 (д r r )

д f д ²     1 д     1    1 , ₇) _m

+—I---+----+ L ² \w ⁽¹⁾ ₇

д 9 (д r ² r д r  r ² 2    )

(П4)

(П5)

(П6)

(П7)

Здесь b ⁽¹⁾ =----- .

2 µ ⁽¹⁾