Амплитудно-частотный отклик распределенного акустического сенсора DAS со спиральной намоткой волокна

Распределенные системы регистрации акустических сигналов с помощью оптоволокна (DAS – distributed acoustic sensing) хорошо известны уже несколько лет [1–3]. Однако их внедрение в практику геофизических исследований требует решения определенных практических задач, связанных с физико-геометрическими особенностями таких систем.

Регистрация акустического сигнала в системе DAS осуществляется за счет анализа спектра рэлеевского рассеяния света в оптоволокне, которое возникает при прохождении светового импульса заданной длины волны и длительности. Продольная деформация волокна приводит к изменению амплитудных и фазовых компонент частотных спектров отраженного оптического сигнала [2]. Оптическая интерферометрия позволяет вычислять величину деформации на определенном участке, положение которого может быть найдено по времени прихода отраженного оптического импульса при известной скорости света в волноводе [4, 5]. Единичная база приема L (Gauge Length), на которой производятся измерения, определяется оптоэлектронными характеристиками регистратора. В результате вычисляется профиль распределения напряжений в волокне в определенный момент времени. Повторный опрос ограничивается временем прихода отраженного сигнала от самого удаленного участка оптоволоконной магистрали. Скорость распространения света в оптоволокне составляет 2×10⁸ м/с, и для линии 1 км двойное время пробега импульса света составляет 10^-5 с, а для 100 км – 10^-3 c, что на данный момент является ограничением дискретизации регистрируемого сигнала по времени.

При проведении настоящего исследования была поставлена цель проанализировать возможности распределенных датчиков DAS при решении горнотехнических задач, сравнить с существующими сейсмоаку-стическими системами сбора данных и подготовить основу для проведения сейсмоакустических исследований с регистрацией оптоволоконной распределенной системой.

Спектральный состав сигналов, регистрируемых оптоволоконными датчиками c линейным волок- ном, рассмотрен в работах [6–8]. Поскольку измерения DAS предполагают осреднение измеряемого параметра на базе приема L, возникает искажение спектра акустического сигнала при частотах выше 150–300 Гц [7, 9, 10]. Сигналы со спектром, не превышающим эти значения, подходят для решения задач нефтяной сейсморазведки [3, 11, 12] и мониторинга рудных месторождений [13, 14]. В скважинной и шахтной сейсморазведке верхняя граница частотного диапазона полезного сигнала составляет 1000 Гц и выше [15–17], поэтому необходимо рассмотреть возможности применения распределенных оптоволоконных систем для решения горнотехнических задач, сравнить с существующими сейсмоаку-стическими системами сбора данных. Кроме того, на данный момент в литературе отсутствует анализ амплитудно-частотных характеристик кабеля со спиральным уложением волокна.

Диаграмма акустической направленности прямого оптоволокна

Системы DAS измеряют деформацию оптоволокна вдоль его оси, таким образом, для продольных волн диаграмма направленности определяется как D_P (α) = А ₀cos² α, для поперечных волн D_S (α) = А ₀|sin 2α| [1, 18], где α – угол между волокном и вектором распространения волны; А ₀ – амплитуда падающей волны. Падение сейсмической волны на линейный участок оптоволокна рассмотрено в работах [3, 11, 19]. Такая диаграмма направленности существенно ограничивает круг возможных решаемых сейсморазведочных задач, в частности, во многих стандартных случаях сейсмических исследований целевые волны приходят по нормали к приемной линии.

Применение специальных кабелей с нестандартным уложением волокна может расширить возможности оптоволоконных систем для решения сейсмо-акустических задач. Варианты конструкции кабеля приведены в патенте [20]. Для производства наиболее доступным способом уложения волокна в кабеле является спиральная намотка, натурные измерения описаны в работах [21, 22].

2023;8(1):13–21

Влияние угла намотки на эффективную базу приема кабеля

При спиральной намотке длина волокна, уложенного в кабеле, будет больше, чем длина кабеля. Таким образом, будет изменяться и эффективное значение L_H связанного с кабелем породного массива.

Уменьшение базы приема пропорционально косинусу угла намотки:

L H = L cos 6 ,                    (1)

где θ – угол отклонения направляющей волокна от оси кабеля (для прямого волокна θ = 0°)¹; L – база приема вдоль волокна; L_H – база приема вдоль кабеля со спиральной намоткой волокна.

Алгоритм численного расчета диаграммы направленности кабеля за счет намотки приведен в работах [23, 24].

С увеличением угла намотки волокна появляется чувствительность системы по нормали к оси кабеля. Диаграмма направленности для продольных волн меняется с диаграммы одноосевого датчика в сторону диаграммы датчика давления, имеющего равномерную (сферическую) диаграмму.

Чувствительность равномерно распределяется по осям при значении угла намотки

6 = arccos I     U 54,7 ° [19,23].

I V3 J

Влияние угла намотки на чувствительность кабеля

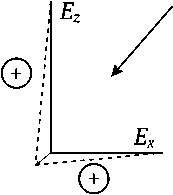
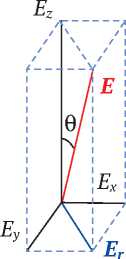
При изменении диаграммы направленности кабеля за счет намотки можно представить единичный отрезок спирали в виде линейного участка с эквивалентным распределением чувствительности по осям (рис. 1). В параметрическом виде энергия сигнала будет распределяться следующим образом:

Ez = E cos2 6;

Er = E sin2 6;

Ex,y = 2 E sin2 6,

Таким образом, при равномерной диаграмме направленности (шарообразной) по одной оси зарегистрированная энергия будет в 3 раза меньше и амплитуда сигнала уменьшится в 3 раз.

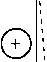
Суммарный сигнал от воздействия сейсмической волны со спиральным волокном складывается из ее взаимодействия с эквивалентными участками, разложенными по ортогональным осям. Для продольных волн сигналы буду складываться, а для поперечных – вычитаться (рис. 2).

a

где E – полная чувствительность; E_z , E_r , E_x , E_y – чувствительности соответственно по оси z , в плоскости, перпендикулярной оси z , по осям x и y .

P

б

E z

S

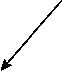
E x

E H = E z + E x

E H = E z – E x

Рис. 2. Схема изменения длины волокна под воздействием продольных ( а ) и поперечных ( б ) волн

Диаграмма направленности симметрична относительно оси кабеля и зависит от углов намотки и падения сейсмической волны в соответствии с выраже-ниеми (2–4):

D P (a, 6) = cos² a cos² 6 + 2 sin² a cos² 6; (5)

Рис. 1. Распределение чувствительности по осям при спиральной намотке волокна

D S (a, 6) = |sin2a cos²

—sin2a sin2 6

На единице длины кабеля увеличение зарегистрированной энергии будет происходить за счет увеличения длины волокна и количества трасс вследствие уменьшения эффективной базы приема согласно формуле (1).

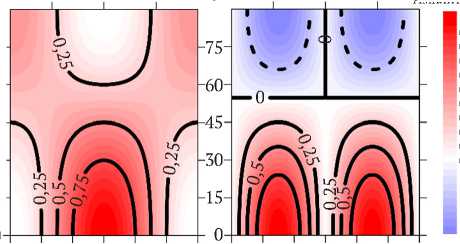
где D_P , D_S – направленность соответственно для P и S волн; α – угол между кабелем и лучом сейсмической волны. В графическом виде диаграммы приведены на рис. 3.

Заметим, что полученные данные отличаются от приведенных в работе [23], где полярность сигнала S -волн меняется в зависимости от направления распространения оптического сигнала в волокне. Однако это означало бы, что измерения на одном и том же участке кабеля путем подключения с разных концов оптической линии давали бы различные результаты.

2023;8(1):13–21

а

Амплитуда

Зависимость

б

Cti к

Угол падения, град

Угол падения, град

–90 –60 –30 0 30 60 90 –90 –60 –30 0 30 60 90

1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1

0 –0,1 –0,2 –0,3 –0,4 –0,5

амплитудно-частотных характеристик от угла падения волны

При расположении линейного приемника в поле гармонической волны (рис. 5) видимый период будет увеличиваться при увеличении угла а между направлением распространения волны и линией приема от 0° до 90°. Видимая частота, в свою очередь, будет уменьшаться:

Рис. 3. Зависимости чувствительности кабеля со спиральным уложением волокна от углов падения волны и намотки волокна для P ( а ) и S ( б ) волн

Частотные характеристики регистрируемого сигнала для прямого волокна

Рассмотрим момент времени, когда монохроматическая упругая волна с частотой колебаний f создала продольные напряжения в волокне, растянутом вдоль оси z . В этом случае амплитуда регистрируемого сигнала будет изменяться согласно выражению

A( x) = A0 sin( kz), где k = 2nfIV- волновое число; A0 - максимальная амплитуда сигнала.

Амплитуда сигнала, измеренного на отрезке длины L , равна сумме амплитуд вдоль этого отрезка:

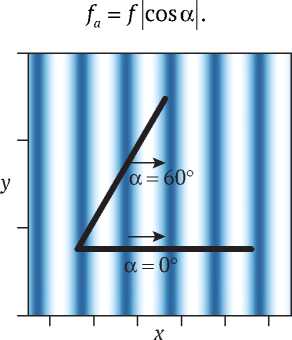
Рис. 5. Изменение видимого периода при разных углах подхода волны

Для участка прямого волокна и произвольного угла падения волны а зависимость АЧХ от угла падения может быть найдена как произведение амплитудной характеристики (7) и диаграммы направленности, с учетом видимой частоты вместо действительной (8):

L

A L = A J sin( kz ) dz = A

V

2 n f

1 - cos

Г 2 n fL ))

.

I V ))

V a l ^{( а} , ^f ) = A o ^{2 п} f a

г

1 - cos

V

Г 2 п Lf a ))

I V JJ

D ( а ).     (9)

Здесь мы видим, что, во-первых, с ростом частоты амплитуда сигнала падает. Во-вторых, в точках, удовлетворяющих условию L = n X, n e Z , функция принимает нулевое значение. В результате амплитудно-частотная характеристика (АЧХ) осложнена участками ослабления сигнала в результате действия прямоугольного оконного фильтра, каким представляется протяженный линейный приемник. АЧХ для продольных волн, распространяющихся вдоль волокна со скоростью V = 2500 м/с, и базы измерения L = 10 м приведена на рис. 4.

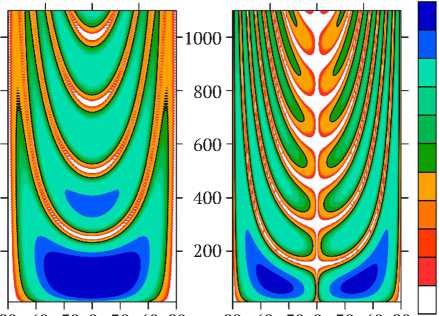
Изображение данной зависимости для продольных и поперечных волн при L = 10 м, V_P = 2500 м/с, V_S = 1500 м/с представлено на рис. 6. На изображении обращают на себя внимание участки режекции в виде «улыбок» и малая чувствительность при углах, близких к 90°.

аб Амплитуда

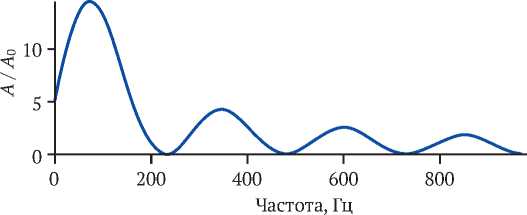
Рис. 4. Амплитудно-частотная характеристика участка прямого волокна при прохождении волны вдоль него

Угол падения α , град

Угол падения α , град

0,8

0,6

0,3

0,1

0,08

0,06

0,03

0,01

Рис. 6. Амплитудно-частотная характеристика участка прямого волокна при различных углах падения упругой волны для P ( а ) и S ( б ) волн

2023;8(1):13–21

Амплитудно-частотный отклик спирального волокна

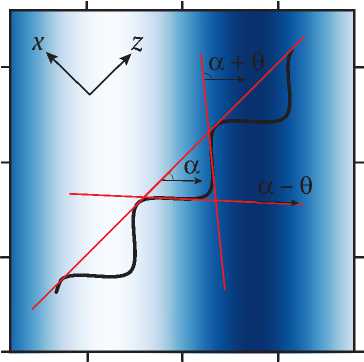
Далее рассмотрим кабель радиуса r со спиральным уложением волокна, на который волна падает под углом а. Угол падения волны на отдельные малые участки равен а + ф( z ) (рис. 7), где ф( z ) можно найти через производную функции, описывающей спиральное волокно в плоскости ( z, x ):

I ,„^е I x ( z ) = r Sin z tg   ,

I r )

откуда

I                i         9

ф(z) = arctg tg 9 cos z tg— I            I       r

Функция ф( z ) принимает значения от -9 до 9, и при условии, что длина волны намного больше шага между витками в кабеле, отклик будет равен сумме

A h ( f , 9 , а ) = £ A l ( f , а + ф ( z)) A L ( ф )/ L ,    (12)

ф=-9

в результате отклик становится более равномерным по углам падения. По частотам присутствуют провалы чувствительности, хотя и менее выраженные, чем для прямого волокна, что оставляет возможности для отбеливания спектра.

Важным случаем здесь является угол падения волны 90°, отклик при котором вынесен отдельно на рис. 10. Из графиков видно, что есть полосы частот, в которых происходит увеличение амплитуды сигнала при увеличении угла намотки, и полосы, где усиление не происходит.

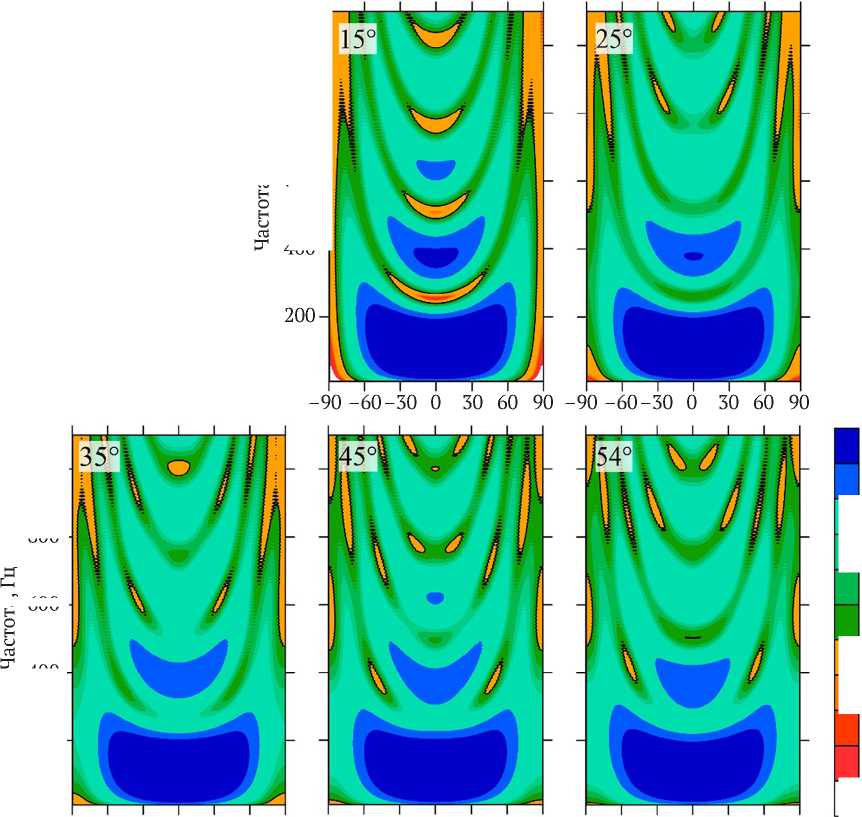
С увеличением угла намотки эффективная база приема уменьшается в соответствии с формулой (1), что, в свою очередь, приводит к увеличению частоты первого минимума в суммарном частотном отклике. Данный факт позволяет при суммировании сигналов с прямого и спирального волокна получить более равномерную частотную характеристику в большом диапазоне углов падения волны на кабель (рис. 11), за исключением углов падения, близких 90°, где АЧХ зависит только от спирального волокна.

где множитель ^L (ф)/ L выполняет роль весового коэффициента, зависящего от доли участков с фиксированным значением угла ф в общей длине волокна. Распределение углов можно найти путем вычисления производной функции z ( x ) = r ctg 9 arcsin ( x / r ):

dz dx

ctg 9

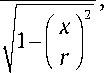
для которой x e [- r , r ] и углы меняются от -9 до 9. Пример распределения ф для угла намотки 45° приведен на рис. 8.

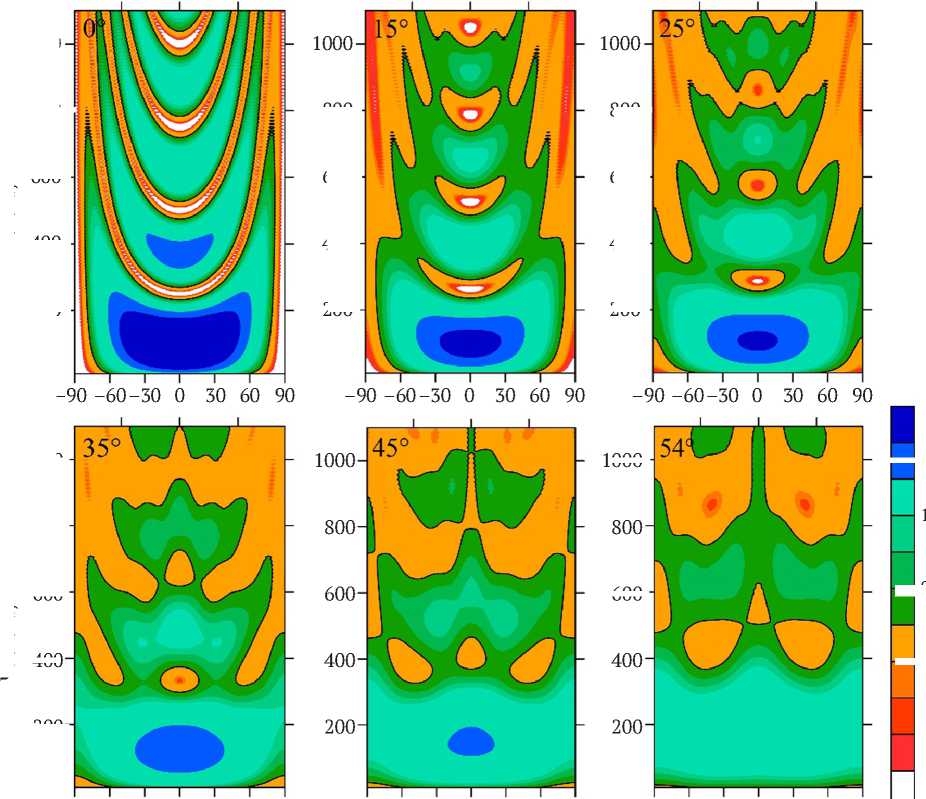
Для продольных волн по формуле (12) получены амплитудно-частотные характеристики для различных углов намотки волокна в кабеле (рис. 9). С увеличением угла намотки полосы режекции размываются,

Радиус изгиба волокна в спиральном кабеле

Стандартное телекоммуникационное волокно имеет определенную линейку типоразмеров и маркировок, при этом одной из основных характеристик является зависимость коэффициента затухания сигнала от радиуса изгиба волокна.

Радиус изгиба определяется в плоскости, в которой он максимален. При равномерной спиральной намотке радиус кривизны постоянный и совпадает с радиусом минимальной кривизны эллипса, образуемого при сечении кабеля плоскостью под тем же углом, что и угол намотки (рис. 12). Таким образом, эффективный радиус кривизны волокна будет зависеть от радиуса заложения волокна в кабеле r и угла намотки 9:

e sin2 9

.

0,8 0,6 0,4 0,2

–0,2 –0,4 –0,6 –0,8 –1

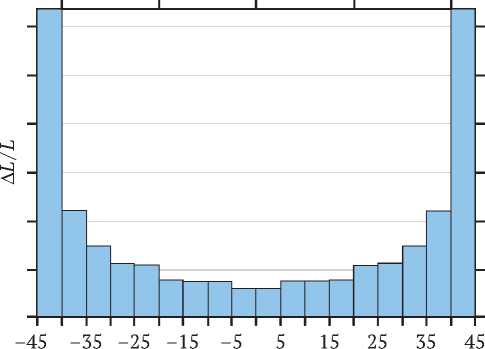
Угол наклона волокна в кабеле, град

Рис. 8. Распределение углов наклона волокна относительно оси кабеля при спиральной намотке 45 °

Амплитуда

Рис. 7. Спиральное волокно в поле плоской упругой монохроматической волны

2023;8(1):13–21

Частота, Гц                                 Частота, Гц

5,5

0,55

0,1

0,055

–90 –60–30 0 30 60 90

–90 –60–30 0 30 60 90

Угол падения, град

–90 –60–30 0 30 60 90

Угол падения, град

0,01

Амплитуда

Угол падения, град

Рис. 9. Амплитудно-частотные характеристики кабеля для различных углов намотки волокна

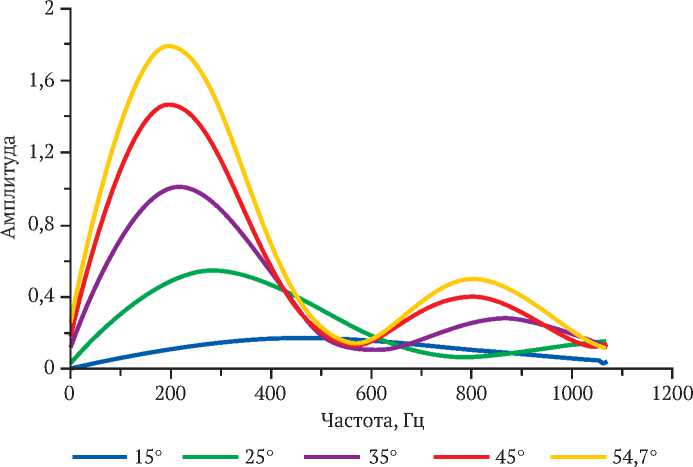
Рис. 10. Поперечная чувствительность кабеля со спиральным уложением волокна при различных углах намотки

2023;8(1):13–21

лГ 600

СУ 600

0,8

0,6

0,3

0,1

0,08

0,06

0,03

–90 –60–30 0 30 60 90

–90 –60–30 0 30 60 90

Угол падения, град

–90 –60–30 0 30 60 90

Угол падения, град

Амплитуда

0,01

Угол падения, град

Рис. 11. Амплитудно-частотные характеристики суммарного сигнала с прямого и спирального волокна с различными углами намотки

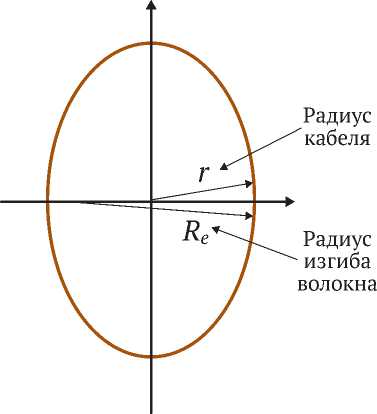
Рис. 12. Схема определения эффективного радиуса изгиба волокна

2023;8(1):13–21

Принимая R_e в качестве фиксированного значения, определяемого выбранным типом волокна, можно получить зависимость радиуса кабеля от угла намотки 9: r = R e sin² 9 . Масса такого кабеля будет пропорциональна sin⁴ 9.

Для волокна стандарта G657.А2 радиус изгиба, при котором не возникает потерь на значительном количестве витков, составляет 30 мм. Исходя из такого значения радиуса и угла намотки 45° спроектирован кабель, содержащий одновременно прямое и спиральное волокно. Внешний диаметр кабеля составляет 32,6 мм, масса 721 кг/км. Такой кабель может быть использован как для поверхностных сейсмических измерений, так и для скважинных.

Заключение

Анализ физико-геометрических процессов регистрации акустических сигналов распределенной оптоволоконной системой позволил получить пространственно-временные характеристики таких систем для прямого и спирального уложения волокна в кабеле.

Амплитудно-частотные характеристики сигналов, регистрируемых спирально закрученным волокном, зависят от нескольких ключевых факторов: интегрирования измеряемого значения вдоль волокна на базе измерения, угла падения волны на кабель и угла намотки волокна в кабеле. Удалось показать, что увеличение угла намотки повышает равномерность амплитудно-частотной характеристики продольных волн как по частотам, так и по углам падения.

В то же время спиральная намотка меняет эффективную базу измерения сигнала, что позволяет путем суммирования сигналов прямого и спирального волокна за счет перекрытия спектров выполнять регистрацию частот, подавляемых при раздельной регистрации.

По результатам исследования предложена конструкция кабеля для регистрации широкополосных сейсмоакустических сигналов, с помощью которых можно выполнять сейсморазведочные исследования как в скважинах, так и на поверхности, и решать обширный круг горнотехнических и инженерных задач.

Sudakova M. S., Belov M. V., Ponimaskin A. O. et al. Features of processing vertical seismic profiling data of offshore shallow wells with fiber-optic distributed systems. Journal of Geophysics . 2021;(6):110–118. (In Russ.)

2023;8(1):13–21

Sanfirov I. A., Yaroslavtsev A. G., Chugaev A. V. et al. Frozen wall construction control in mine shafts using land and borehole seismology techniques. Journal of Mining Science . 2020;56(3):359–369. https://doi . org/10.1134/S1062739120036641