Амплитудно-импульсная модель силовых цепей стабилизаторов напряжения

Импульсные стабилизаторы напряжения (ИСН) находят широкое применение в автономных системах электропитания, например в системах электропитания космических аппаратов [1]. В таких системах к выходу ИСН подключаются несколько потребителей электроэнергии, взаимодействующих через общее выходное напряжение стабилизатора. При этом система «ИСН-потребители» может стать неустойчивой. Обеспечить ее устойчивость можно снижая выходной импеданс ИСН путем повышения его быстродействия [1].

Из всех известных подходов к синтезу законов управления, обеспечивающих ИСН с широтно-импульсной модуляцией (ШИМ) высокое быстродействие, особый интерес представляет метод [2], заключающийся в следующем:

• -    представлении силовых цепей ИСН с ШИМ в режиме малых отклонений адекватной амплитудно-импульсной моделью по регулируемым составляющим процессов;

• -    синтезе закона управления с использованием полиномиальных уравнений [3] синтеза систем с амплитудноимпульсной модуляцией (АИМ);

• -    реализации синтезированного закона управления в ИСН с учетом специфики ШИМ.

Этот метод [2] позволил его авторам синтезировать закон управления, обеспечивающий минимальную конечную длительность переходных процессов в ИСН с силовой цепью понижающего типа (рис. 1).

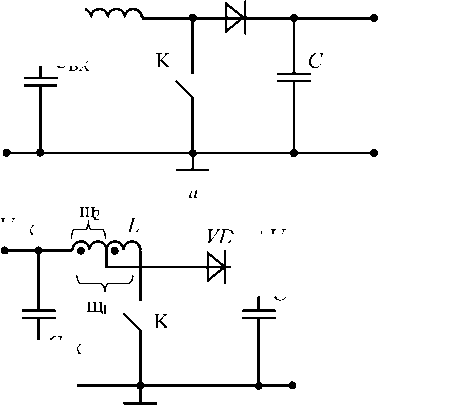
В то же время авторы этого метода не смогли применить его для синтеза быстродействующих ИСН с силовыми цепями повышающего (рис. 2), инвертирующего (рис. 3) типов и модификаций всех рассматриваемых типов ИСН из-за отсутствия амплитудно-импульсных моделей этих стабилизаторов по регулируемым составляющим процессов. На практике широко применяются ИСН всех рассматриваемых типов и модификаций. В связи с этим задача определения их амплитудно-импульсных моделей по регулируемым составляющим процессов актуальна и ее решение необходимо для синтеза законов управления и анализа процессов в ИСН.

Рассмотрим разделение общего процесса изменения переменных состояния в ИСН с ШИМ на стационарный процесс, соответствующий неизменной (стационарной)

длительности ^импульсов управления регулирующим элементом (РЭ) и процесс регулирования, обусловленный приращением длительности t ^ импульса управления на величину t_ир относительно стационарной длительности t ^ . Полезную информацию о процессе регулирования несут только регулируемые составляющие. Для процесса регулирования в режиме малых отклонений, когда t ^ _р<<  Т , где Т - период преобразования, переход от системы с ШИМ к системе с АИМ осуществляется путем замены регулируемой составляющей импульсов напряжения U_{L р}(t), воздействующих со стороны РЭ на дроссель и имеющих длительность t_ир (t), эквивалентными по вольт-секундной «площади» 8 -функциями.

В качестве примера на временных диаграммах (рис. 4) приведен процесс изменения напряжения U_L (t) и тока I_L (t) дросселя L и напряжения U_c(t) на емкости конденсатора С в схеме (рис. 2, а) с разделением на регулируемую (помечена индексом «р») и стационарную (помечена индексом «ст») составляющие. Рассмотрен режим неизменного тока нагрузки ИСН.

Для всех схем регулируемая составляющая напряжения U_Lр(t) на дросселе L имеет вид двухполярных импульсов с амплитудой U_L^_A(t) и длительностью t_ир (t). Амплитуда U_{L р A}(t) регулируемой составляющей напряжения определяется как разность напряжений U_{L нак}(t) и U_{L рас}(t) на дросселе L на интервалах накопления и расходования энергии дросселя:

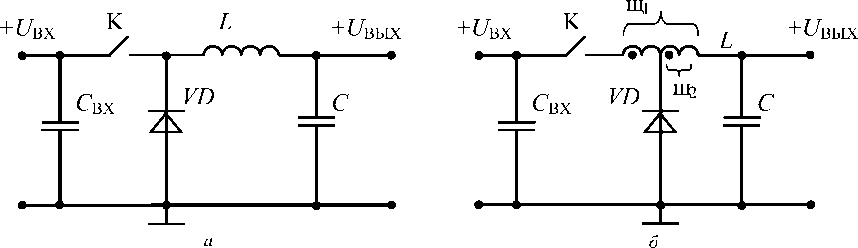
+ ^ вых

VD i

L

+ ^ вх

TV

С

С вх

К

К

в

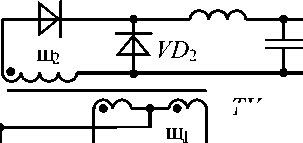
Рис. 1. Силовая цепь понижающего типа и ее модификации

+U bx

L

VD

+ ^ вых

С вх

С вх

б

Рис. 2. Силовая цепь ИСН повышающего типа и ее модификация

Wbx

+ ^ вых

С

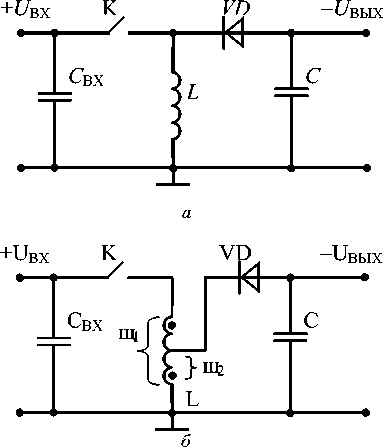
Рис. 3. Силовая цепь ИСН инвертирующего типа и ее модификация

^( t )^-^)-^) .      (1)

Например, на интервале накопления энергии ключ К включен, в ИСН и повышающего, и инвертирующего типов ULнак(t) — U (t). На интервале расходования энергии ключ К выключен, и в повышающем ИСН UL (t) — UBX(t) - UBЫX, а в инвертирующем ИСН ^рас^ — - UBb№ ГДе UBX(t) и UBЫX - напряжения на входе и выходе ИСН соответственно. Следовательно, в повышающем ИСН и, ,(t) — и. (t)-U, (t) — ив,IY,

L.р.A          L.нак         L.рас          BЫX, а в инвертирующем ИСН

U Af) = U, (t)-U (t) — U_Y(t) + U_H,_IY.

L. р . A          L. нак         L. рас         BX         ВЫХ

U k

T

, te.p.

mT

(mlllT

(m^2)T

U h^xJ» -_^вы^_

I t ? 9.ct

^{I l} p

U l ._p

^U c . p

^U c . n

I^L p.

I l . p.

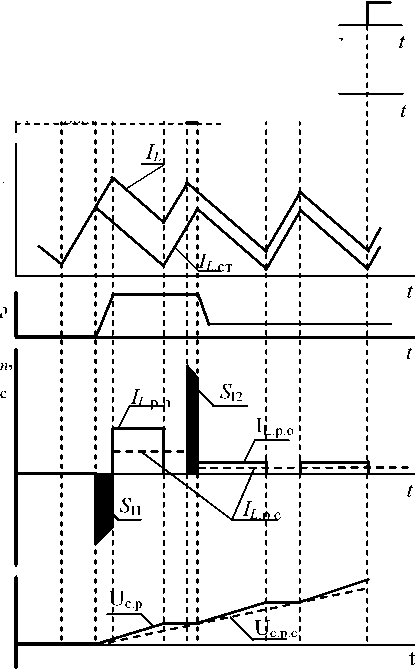
Рис. 4. Bременные диаграммы, поясняющие выделение регулируемых составляющих процессов

Аналогично с использованием выражения (1) определены амплитуды U_{L рА}(t) регулируемых составляющих напряжения на дросселе для всех рассматриваемых схем. Особенность определения U_{L рА}(t) для схем с автотрансформаторным включением дросселя состоит в том, что амплитуда U_{L р A}(t) определяется как амплитуда напряжения не на всем дросселе, а на его части с числом витков ю ₂, которая через диод VD подключается к конденсатору С и выходу ИСН. При этом U_{L нак}(t) —К^ U_L(t), где К — ю ₂/ ю ₁ - коэффициент трансформации, а U_L (t) - напряжение, приложенное ко всему дросселю L на интервале накопления энергии.

B отличие от ИСН понижающего типа в ИСН повышающего и инвертирующего типов и их модификациях ре гулируемая составляющая тока IL р(t) дросселя L передается в конденсатор С только на интервалах проводящего состояния диода VD. Эта передаваемая часть^ р Jt) регулируемой составляющей токаILр(t) дросселя приведена на соответствующей временной диаграмме (рис. 4). Bы-деленные на ней штриховкой ампер-секундные «площади» тока 5 и S вызваны не регулируемой составляющей тока IL р(t) дросселя, а объясняются изменением длительности передачи стационарной составляющей тока IL ст(t) дросселя в конденсатор С.

A. B. Манаков, B. И. Иванчура, Б. П. Соустин показывают, что для случая малых отклонений и при управлении ИСН, обеспечивающем минимальную конечную длительность переходных процессов, ампер-секундные «площади» 5 и S_{I 2}, примерно равные по модулю и противоположные по знаку, взаимно компенсируются. Поэтому можно пренебречь их влиянием на изменение регулируемой составляющей напряжения и_с . _р на емкости С конденсатора [2].

Поскольку в схемах, приведенных на рис. 2 и 3, регулируемая составляющей тока^ _р Jt) дросселя L передается на выход ИСН на интервалах проводящего состояния диода VD , то среднее за период Т значение передаваемой регулируемой составляющей тока дросселя

^С0=КсЛр.С0, где Ксв — (1 - Кзст) - коэффициент связи (относительное время проводящего состояния диода), а К — t /Т -стационарный коэффициент заполнения импульсов управления UK ключом К, на соответствующей временной диаграмме ILрс(t) показана пунктиром. На временных диаграммах UCр(t), U(j) показаны регулируемые составляющие напряжения на емкости конденсатора С, обусловленные регулируемыми составляющими тока дросселя ILрп(t) и ILрс(t), соответственно. Поскольку в моменты времени тТ регулируемые составляющие напряжений Uc_(mT) и Ц.р с(тТ) равны, то в амплитудно-импульсной модели ИСН реальную дискретную связь дросселя L с конденсатором С можно заменить на непрерывную посредством звена с коэффициентом передачи К .

Общее правило для определения Ксв можно записать следующим образом:

КгК^^а-^ (2)

где К - коэффициент передачи на выход регулируемой составляющей тока дросселя L или его обмотки с числом витков ю ₂ на этапе накопления энергии дросселя. Для схем, приведенных на рис. 2 и 3 К — 0. B схеме, приведенной на рис. 1,6К — ю ₂/ ю ₁, а в остальных схемах К_{п нак} — 1. Коэффициенты связи для всех рассматриваемых схем, полученные с использованием уравнения (2), сведены в таблицу, где^ - U_BЫX/U_BX, а К_тр - ю ₂/ ю ₁.

B ИСН (рис. 1, а) при выполнении следующих условий:

_ 1/®ф»Ти^»Т, (3) где Щф - 1/ 4LС , TL — L/Rl, L и Rl- индуктивность и активное внутреннее сопротивление дросселя, а С - емкость конденсатора фильтра, и законе управления, обеспечивающем минимальную конечную длительность переходных процессов, можно пренебречь влиянием емкостного накопителя энергии на индуктивный, а саму непрерывную часть представить в виде последовательно функциями ^.(р) =1/(pL) и ^С(р) = 1/(рС), соответствен-включенных дросселя и конденсатора с передаточными но [2].

Схема (номер р0сонка)	Стат0ческ0й коэфф0ц0ент 3аполнен0я К ГТ J. с1	Ампл0тода регал0раемой составляющей напряжен0я дросселя U L oA	Коэфф0ц0ент связ0 Ксв
1 , а	K U	U вх	1
1 ,б	K u К тр + K U (1 - K ТР )	К ТР U вх — ( К ТР — 1) U вых	1 + ( К ТР — 1) К 3.СТ
1, в	К тР К и	К ТР и вх	1
2 , а	К и — 1 K U	U вых	1 - К 3.СТ
2 , б	К и - 1 К и — 1 + К тр	( К ТР - 1) U вх + и вых	1 - К 3.СТ
3 , а	K U 1 + К и	U вх + U вых	1 - К 3.СТ
3 , б	К и К ТР + К и	К ТР и вх + U вых	1 — К 3.СТ

Если в рассматриваемых ИСН выполняются условия (3), а закон управления обеспечит им те же свойства [2], то амплитудно-импульсная модель силовой цепи для всех ИСН, с учетом наличия К , примет вид, приведенный на рис. 5. Входной сигнал S _e( t) = U_L (г) ^ (О модулятора определяется из условия замены регулируемой составляющей импульса эквивалентной по вольт-секундной «площади» 8 -функцией. Коэффициент связи К и амплитуда регулируемой составляющей напряжения U_{L рА}(^) для каждого ИСН индивидуальны и приведены в таблице.

С целью подтверждения универсальности модели с использованием метода [2] синтезированы законы управления повышающим и инвертирующим ИСН. Исследования динамических характеристик этих ИСН, проведенные с использованием макетов и математических моделей в формате Pspise, подтвердили достижение минимальной конечной длительности переходных процессов при «малых» возмущающих воздействиях со стороны нагруз ки. В качестве примера на рис. 6 приведены временные диаграммы тока дросселя IL и выходного напряжения UBHX в ИСН повышающего типа при ступенчатом изменении тока I. При изменении тока нагрузки, вызывающем приращения длительности импульса управления ^ир << Т, длительность переходного процесса составляет два периода преобразования (рис. 6, а). При больших изменениях тока нагрузки и нарушении условия ^ир << Т, длительность переходного процесса увеличивается (рис. 5, б), что объясняется неадекватностью амплитудно-импульсной модели ИСН для случая значительных приращений длительности импульса управления силовым ключом в ИСН с ШИМ.

Разработанная амплитудно-импульсная модель по регулируемым составляющим процессов является универсальной и может использоваться в целях синтеза законов управления ИСН со всеми основными типами силовых цепей, имеющими индуктивный и емкостной накопители энергии.

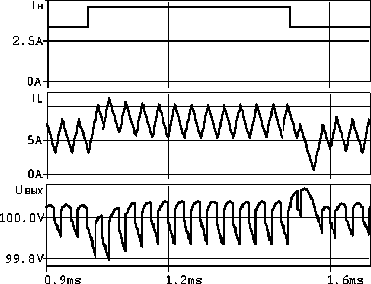
Рис. 5. Универсальная амплитудно-импульсная модель

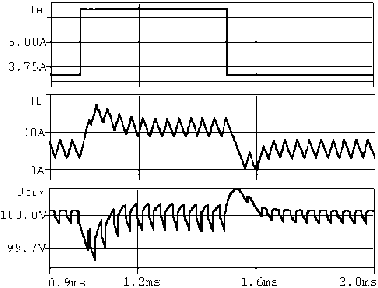
а                                         б

Рис. 6. Временные диаграммы процессов в ИСН повышающего типа