Амплитудно-зависимый гистерезис скорости волны в горных породах в широком диапазоне частот: экспериментальное исследование

Введение и постановка проблемы

Перспективный подход к повышению геологической эффективности сейсмических и акустических методов исследования опирается на новые знания в физике деформирования горных пород. Под этим подразумевается глубокое изучение механизмов распространения и затухания упругих волн на микро- и наноуровне. К списку малоизвестных знаний можно отнести свойство микропластичности горных пород, которое проявляется при малых деформациях. Интересы в науках о Земле охватывают большой частотный диапазон квазистатических и динамических напряжений и деформаций.

Динамические характеристики пород при сейсмических воздействиях были изучены на больших и умеренных деформациях [1]. С изучением нелинейных эффектов в сейсмике [2–7] вопрос о границе «упругость–неупругость» стал более актуальным. С учетом (исходя из) экспериментальных данных уровень деформации этой границы был постепенно сдвинут от ~ 10-2 – 10-3 в сторону меньших деформаций до ~ 10-6. Таким образом, было показано, что нелинейные эффекты в горных породах возможны даже при малых деформациях. Это расширяет действие неупругих процессов на область практического применения, где используют волны малой интенсивности.

В настоящее время теоретические исследования в сейсмике опираются на классическую вязкоупругую модель стандартного линейного тела, которая хорошо описывает дисперсию, релаксацию и связанные с нею неупругие процессы [8, 9]. Однако эта модель не учитывает такой нестандартный эффект, как амплитудная зависимость скоростей волн и затухания, который обнаружен во многих экспериментах при распространении сейсмических и акустических волн в горных породах [10–13]. В основном это лабораторные эксперименты на образцах твердых пород, извлеченных с больших глубин. Экспериментальные данные показывают, что с увеличением амплитуды излучаемого сигнала наблюдается уменьшение скорости волны и увеличение затухания [9, 14, 15]. Другие эксперименты также подтверждают представленные выше данные, но одновременно имеют и противоположный результат. С увеличением амплитуды сигнала может происходить как увеличение, так и уменьшение скорости волны, и затухания [6, 11]. Необычное поведение скоростей волн распространяется на поведение модуля упругости. Уменьшение или увеличение модуля упругости происходит в соответствии с кривизной соотношения напряжение–деформация [16–20].

Микропластическая неупругость горных пород была обнаружена в квазистатических экспериментах на различных образцах [19]. Микропластичность металлов, сплавов и других материалов была известна. Ее проявления на диаграмме «напряжение–деформация» представлены в виде «стресс-плато» и «стресс-падение» (the stress-plateau and the stress-drop) [21–24]. Это свойство можно охарактеризовать как некоторое нерегулярное кратковременное «включение» пластичности внутри упругой области деформирования [16, 25–27]. Это положение имеет также теоретическое подтверждение [28, 29]. Ниже представлены результаты исследования амплитудной зависимости скорости продольной волны в породах, полученные с использованием различной аппаратуры в различных условиях проведения эксперимента.

2021;6(1):23–30

Методики исследования и фактический материал

Полевые исследования

Полевые измерения проведены в зоне малых скоростей в суглинках. В верхней части до глубины 8,5 м породы частично водонасыщенны. Скорость продольных волн составляет около 340 м/с. Ниже располагается водоносный горизонт, скорость волны в котором ~ 1500 м/с. Измерения проведены методом межскважинного просвечивания, расстояние между скважинами составляет 7 м. В первой расстановке излучатель установлен на глубине 2 м, а приемник сигналов на глубине 10 м (2 м – 10 м). Волна проходит преимущественно через частично водонасыщенную породу. На второй расстановке излучатель и приемник находятся на глубине (10 м – 10 м), волна распространяется в полностью насыщенной водой породе.

Излучатель сейсмического сигнала состоит из набора пьезоэлектрических шайб, размещенных в корпусе с предварительным усилителем [4, 30]. Излучение сигнала происходит через жидкостную прокладку и герметичную эластичную оболочку, которая контактирует со стенкой скважины. Амплитуда импульса на пьезоэлектрическом преобразователе излучателя изменялась от 350 до 950 В. Использовался датчик ПДС-21, который имеет коэффициент преобразования 100 мкВ/Па. Приемник сигналов контактировал со стенками скважины через эластичную прокладку с жидкостью. Регистрация осуществлялась с накоплением сигнала до 128. Цифровая запись сигналов осуществлялась на компьютере. Точность измерения времени распространения импульса составляла ~ 0,02 %. Время квантования записи t _квант = 8 мкс и 40 мкс. Диапазон амплитуды деформации (3,8 - 9,8) х 10^-8.

Лабораторные измерения в низком килогерцовом диапазоне частот

Эксперименты выполнены на образце песчаника цилиндрической формы диаметром 76 мм и длиной 1 м. Плотность породы – 2,0 г/см³, пористость около 3 %. Скорость распространения продольной волны (2910–3000) м/c. Эксперимент проводился при комнатной температуре на пяти величинах амплитуды деформации (0,3-1,67) х 10^-6.

Излучатель и приемник акустических сигналов, состоящий(е) из пьезокерамических шайб (ЦТБС-3), жестко закреплены на одном конце стержня. На другом конце образца таким же образом жестко закреплена латунная шайба толщиной 3 мм. Вся конструкция через домкрат вставлена в проем стены. Акустический импульс частотой 6835 Гц, пройдя вдоль стержня, отражается от противоположного торца и поступает на приемник и через усилитель на цифровое регистрирующее устройство. Время квантования АЦП регистратора составляет 1 мкс. Точность измерения скорости волны – 0,05 %. Относительная точность измерения, определяемая при вариации амплитуды и постоянстве остальных условий, намного выше.

Лабораторные измерения на частоте около 1 МГц

Исследования проводились на образцах сухого песчаника цилиндрической формы длиной 2,4 см и 4,0 см в диаметре. Мелкозернистый песчаник с присутствием алевролита отобран из скважины с глубины 2920 м. Плотность породы 2,36 г/см3, общая пористость – 13 %. Измерительная установка представляет из себя трехслойную модель. Первый и третий слои (бериллиевая бронза) обеспечивают идентичное отражение волны на границах раздела. Первый слой играет роль линии задержки, а третий слой – акустической нагрузки. Образец породы находится между этими слоями. Возбуждение и прием сигналов обеспечивают пьезокерамические датчики на частоте ~ 1 МГц, которые поляризованы на продольную волну. Контролируемое статическое давление (20 МПа) обеспечивает постоянство контакта на границах слоев.

Результаты исследований

Полевой эксперимент

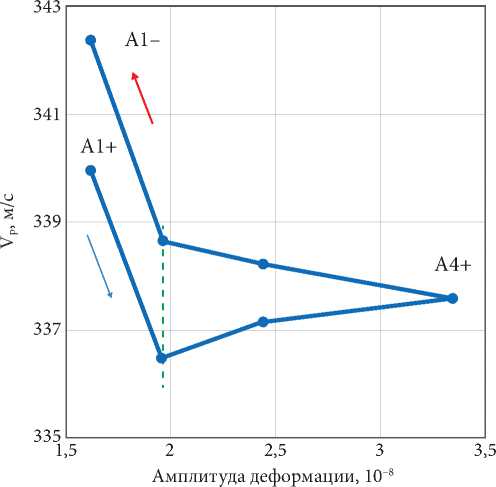
Поведение скорости продольной волны в зависимости от амплитуды деформации в суглинках представлено для двух позиций расположения источника и приемника: расстановки (2 м – 10 м) и (10 м – 10 м). На рис. 1, а показана зависимость скорости продольной волны от амплитуды при расположении источника на глубине 2 м, а приемника на 10 м. Величина амплитуды излучаемого сигнала изменялась дискретно по замкнутому циклу. Увеличение амплитуды идет от А1, А2, А3 до А4 (восходящий полуцикл), а затем ее уменьшение по тем же значениям до А1 (нисходящий полуцикл) – и получаем комплект цифровых записей в полном цикле.

Поведение скорости продольной волны в суглинках в зависимости от амплитуды деформации является сложным. В первом полуцикле курса амплитуды скорость волны сначала уменьшается, а затем нелинейно увеличивается. Во втором полуцикле идет немонотонное возрастание скорости волны. Наибольшее изменение скорости волны в цикле составляет 1,7 %. Имеется явное расхождение «путей» скорости волны между восходящим и нисходящим полуциклами. В диапазоне А2 – А4 скорость волны вместо понижения возрастает. По завершении полного цикла имеется незамкнутая петля гистерезиса, которая составляет 0,7 %. Это эффект амплитудно-зависимого гистерезиса скорости продольной волны.

Рассмотрение сейсмической записи показывает наличие нестандартных осложнений на форме волны, которые были опознаны как признаки микропла-стической деформации. Отдельные фрагменты импульсов, записанных на трех величинах амплитуды, представлены на рис. 1, б. Это встроенные кратковременные амплитудные плато, протяженность которых составляет от одного до нескольких tквант = 40 мкс. Мгновенное значение амплитуды импульса на длине плато не изменяется. Эти плато прерывают «нормальный» курс амплитуды, т.е. процесс упругого деформирования и переход к микропластическому течению. Протяженность плато достигает двенадцати квантов, что составляет 480 мкс. Увеличение количества плато приводит к уменьшению крутизны фронта импульса и его затягиванию. Зависимость скорости продоль- https://mst.misis.ru/

2021;6(1):23–30

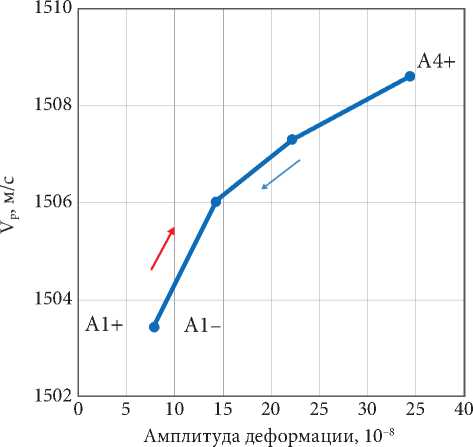
ной волны от амплитуды деформации в суглинках на расстановке (10 м – 10 м) представлена на рис. 2, а . С увеличением амплитуды от А1 до А4 скорость продольной волны нелинейно возрастает на 0,34 %. Здесь, в отличие от предыдущей расстановки, амплитудный гистерезис отсутствует. Это интересный показатель распространения волны в полностью водо-насыщенных суглинках. Цифровые записи также показывают отсутствие плато на форме волны (рис. 2, б ).

Лабораторный эксперимент на низких килогерцовых частотах

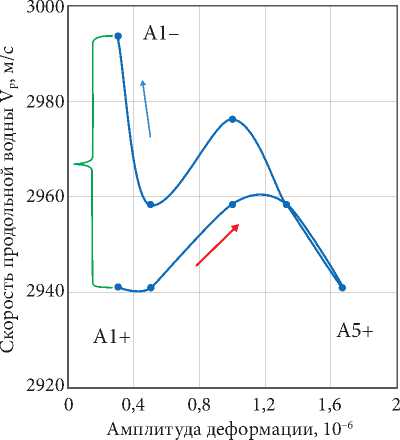
Скорость продольной волны в песчанике в зависимости от восходящей и нисходящей амплитуды деформации представлена на рис. 3, а. При увеличении амплитуды от А1+ до А5+ наблюдается увеличение, а затем уменьшение скорости волны. При уменьшении амплитуды от А5+ до А1– скорость волны с большим с провалом возрастает и наблюдается незамкну-

а

Рис. 1. Скорость продольной волны в суглинках в зависимости от амплитуды деформации: источник на глубине 2 м, приемник – на глубине 10 м ( а ); фрагменты импульсов с осложнениями в виде плато ( б )

Время, секунды

б

а

Рис. 2. Скорость продольной волны в зависимости от амплитуды деформации на расстановке источник-приемник 10 м – 10 м ( а ). Фрагменты фронта импульсов на амплитудах А1–А4 при расстановке h = 10 м – 10 м ( б )

Время, секунды б

2021;6(1):23–30

а

Рис. 3. Фрагменты фронта импульсов на амплитудах А1–А4 при расстановке h = 10 м – 10 м. Демонстрация плато ( а ). Фрагменты импульсов, зарегистрированных на пяти амплитудах, в области первых вступлений ( б )

—•—А1+ —•— А2+ —•—А3+ —•— А4+ —•— А5+

• А4– • А3– —•— А2– —е—А1 – б

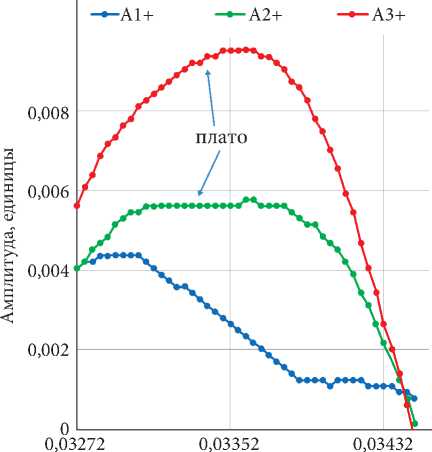
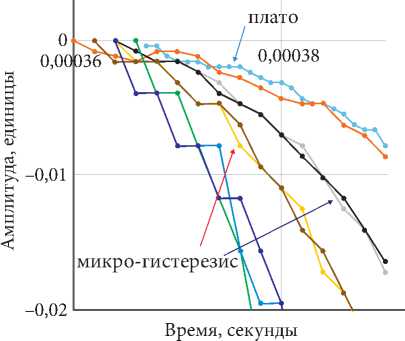
тый гистерезис, который составляет 1,8 %. На рис. 3, б показаны фрагменты фронта импульсов вблизи первого вступления для пяти значений восходящей и нисходящей амплитуды деформации. На акустических трассах присутствуют плато протяженностью более t _квант = 2 мкс. Эти встроенные плато изменяют общий наклон фронта импульса.

На профиле волны обнаружен микрогистерезис. Это кратковременное отклонение двух идентичных трасс (например, А1+ и А1–, А2+ и А2–, и т.д.) от общего амплитудного курса, рис. 3, б . При этом происходит изменение наклона фронта на небольшом участке, т.е. скорости деформирования. Такие участки микрогистерезиса чередуются с участками полного совпадения восходящего и нисходящего курса.

Лабораторный эксперимент на частоте около 1 МГц

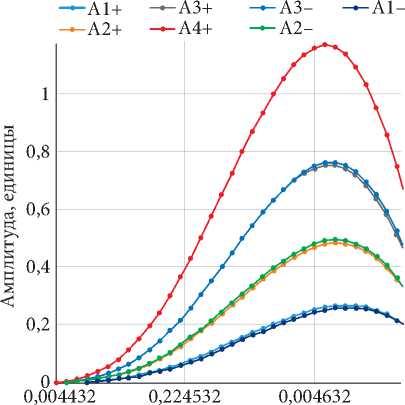
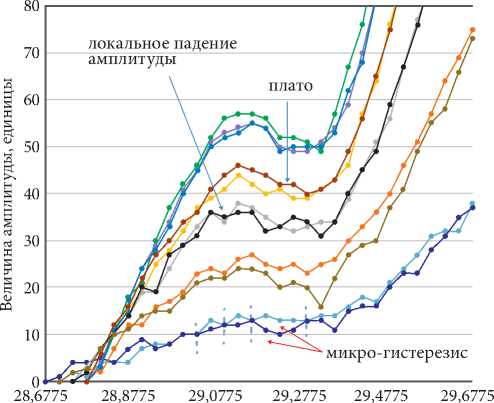
Зависимость скорости волны от амплитуды деформации представлена на рис. 4. При повышении амплитуды величина скорости продольной волны изменяется волнообразно. При уменьшении амплитуды скорость волны нелинейно возрастает на 0,36 %. Амплитудный гистерезис составляет 0,48 %. Форма отраженных импульсов, зарегистрированных с наносекундным разрешением на шести величинах амплитуд при замкнутом цикле измерения, имеет сложную картину деформации. На рис. 5 представлен фрагмент фронта волны, где можно видеть нестандартные неупругие проявления в виде плато, локального падения амплитуды и микрогистерезиса. Протяженность этих осложнений составляет величину в несколько t _квант = 32,5 нс. Следует отметить, что записи (трассы) с восходящей (А+) и нисходящей (А–) амплитудой, несмотря на некоторые отклонения, в целом совпадают.

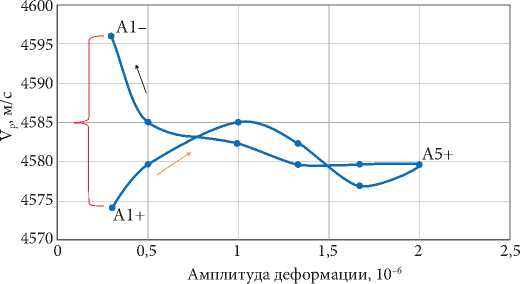
Рис. 4. Скорость продольной волны в песчанике в зависимости от амплитуды деформации

Время, секунды

—•— А1+ —•— А2+ —•— А3+ • А4+ —О— А5+ —О— А6+

—•—А5– —•— А4–  • А3– • А2–  • А1 –

Рис. 5. Фрагменты фронта импульса в песчанике на шести величинах амплитуды

2021;6(1):23–30

Обсуждение результатов

Эффект микропластичности сложным образом зависит от уровня деформации (величины прикладываемого механического воздействия). Эксперименты, проведенные в различных условиях, показывают принципиально одинаковые результаты. Это подтверждает факт влияния амплитуды деформации на скорость продольной волны. Изменение скорости продольной волны за счет амплитуды достигает 2 %. Новейшие исследования, проведенные на образцах горных пород с использованием высокоточной лазерной допплеровской интерферометрии, показывают, что изменение скорости волны за счет амплитуды достигает 5 % [12, 14, 27].

Действие амплитудного эффекта обнаружено на высоких сейсмических и килогерцовых частотах при динамических деформациях примерно 10-8–10-6, которые относятся к области высоких скоростей деформации. Однако ранее полученные результаты квазистатических экспериментов [16, 20, 26, 28] указывают на возможность проявления такого эффекта на более низких частотах. Низкие скорости деформирования твердого тела создают еще более благоприятные условия для срабатывания механизма микропластичности [17, 22]. Замечено, что на низких амплитудах деформации величина амплитудного гистерезиса больше, чем на более высоких амплитудах.

Эксперименты показали «перехлест» петель гистерезиса, а значит и наблюдаемое увеличение или уменьшение скорости волны (модуля упругости). Небольшое изменение величины амплитуды сигнала (один дискретный шаг ∆ А_i ) может приводить к заметному изменению скорости волны. Стандартная (общепринятая) вязкоупругая модель для горных пород такого поведения модуля упругости не допускает. Эф-

фект микрогистерезиса требует тщательного изучения, так как его влияние на динамические параметры волн может оказаться существенным.

Заключение

Эффект амплитудного гистерезиса может быть полезен для практического применения. Отсутствие гистерезиса в полностью водонасыщенной породе побуждает к проведению повторных экспериментов с учетом этого результата. Полученный эффект локального изменения скорости волны в небольшом диапазоне амплитуд деформации имеет как фундаментальное, так и практическое значение. В настоящее время в сейсмических методах чувствительность скорости волны к величине излучаемого сигнала не учитывается, что понижает точность исследования.

В заключение можно сказать, что заинтересованные в этом вопросе организации при желании могут проверить возможность применения амплитудно-зависимого эффекта на практике и определить его полезность для дальнейшего использования. Такая проверка не требует наличия специального оборудования. Используется то же самое оборудование, которое применяется при полевых работах, с некоторыми дополнениями. По крайней мере, высокоточные цифровые регистраторы являются доступными для эксперимента. Изменение величины амплитуды волны методически достигается, например, последовательным изменением мощности источника излучения волны. Учет амплитудного фактора может быть полезен, например, для уменьшения ошибок при построении сейсмического разреза и в других областях геофизических исследований. Возможные области проверки эффекта и его применения: сейсморазведка, ВСП, акустический каротаж и другие.

2021;6(1):23–30