Амплитудные значения падающей и отраженной волн в линии электропередачи трехпроводного исполнения

Транспортировка электрической энергии напряжением 35 кВ и выше до отдаленного потребителя часто выполняется линиями электропередачи (ЛЭП) трехпроводного исполнения. Монтажу, наладке и эксплуатации ЛЭП, как правило, предшествует прогнозирование результатов передачи электрической энергии. Результаты прогнозирования используются при планировании режимов и оперативном управлении, электроснабжения промышленных и иных объектов. При этом трехфазные кабельные линии и сравнительно непротяженные воздушные линии напряжением до 35 кВ в расчетах обычно принимают за линии с сосредоточенными параметрами [1]. Однако в ЛЭП протяженностью свыше 200–400 км заметно проявляется волновой характер распространения электрической энергии в проводящей среде и такие линии электропередачи приходится принимать за линии с распределенными параметрами [2, 3]. А при плохом качестве электрической энергии протяженность ЛЭП, при которой приходится учитывать волновые процессы передачи электрической энергии, уменьшается [4].

Передача электрической энергии обеспечивается волнами электромагнитного поля. Этот

факт является следствием того, что электричество есть результат действия электромагнитного поля.

Токоведущие части неперегруженных ЛЭП можно считать линейной средой. В таком случае получается, что электромагнитное поле распространяется в линейной среде. А такое распространение, как известно из курса физики, выполняется по гармоническим законам [5].

Традиционно анализ результатов транспортировки электрической энергии по ЛЭП выполняется для одного провода, а затем распространяется на остальные провода ЛЭП простым умножением на соответствующий коэффициент. При этом полностью игнорируются электромагнитные связи между токоведущими частями ЛЭП [6, 7]. Это справедливо только при условии практически идеального качества электрической энергии.

Передача электрической энергии по ЛЭП трехпроводного исполнения обеспечивается тремя парами волн электромагнитного поля: тремя падающими и тремя отраженными [8]. Этот факт подтверждается уравнениями распределения фазных напряжений и линейных токов по однородному участку трехпроводной ЛЭП [4]:

U A = 1 E ( A. , , , ,^ ’ i l + A A 2i e - ' ) ;

³ i = 1

.             1

^UB = ?E( A B ( 2 i - 1 ) ^e i ⁺ A B 2 i e i ) ^; "  ³?

^UC = ¹ E ( A c ( 2 i - 1 ) e ^{Y l} + A c 2i e ^-, ‘ l ) ;

³ i = 1

• I A	1	3 E .^	^ A A 2i e - i il	A A ( 2 i - 1 ) e 7 '	+	-Y il A B 2 i e	A B ( 2 i - 1 ) e Y '	+	A C 2i e -i il	A C ( 2 i - 1 ) e Y '	"
	3		Z cAi V	Z cAi		Z cABi	Z cABi		Z cCAi	Z cCAi	7
• I B	= 1	Г 3 . E	f A b 2 i e -' il	A B ( 2 i - 1 ) e Y '	+	A A 2i e -'il	Y i l A A ( 2 i - 1 ) e	+	A c 2 i e -' il	Y i l A C ( 2 i - 1 ) e	> 1
	3		Z cBi V	Z cBi		Z cABi	Z cABi		Z cBCi	Z cBCi	7
• I C	1	. E^	' A C 2i e -Y il	A C ( 2 i - 1 ) e Y '	+	-Y il A A 2 i e	A C ( 2 i - 1 ) e Y '	+	-Y il A B 2 i e	A B ( 2 i - 1 ) e Y '	А1
	3		Z cCi V	Z cCi		Z cCAi	Z cCAi		Z cBCi	Z cBCi	7

где AA2i и AA(2i-1), AB2i и AB(2i-1), AC2i и AC(2i i) — пофазные постоянные интегрирования, характери зующие отраженные и падающие волны i-й пары волн электромагнитного поля; уi - постоянная распро- странения i-й пары волн электромагнитного поля; ZcAi , ZcBi и ZcCi – собственные волновые сопротивле- ния линейных проводов A , B и C i-й паре волн электромагнитного поля; Z cABi , Z cBCi и Z cCAi – взаимные волновые сопротивления между линейными проводами i-й паре волн электромагнитного поля; l – расстояние от начала рассматриваемого участка ЛЭП до места на линии электропередачи, где нужно выяснить численные значения напряжений UA , UB , UC и токов IA , IB , IC .

Для начала анализируемого участка ЛЭП, когда l = 0, уравнения (1)-(4) перепишутся так:

^UA1 = oE( A A ( 2 i - 1 ) ⁺ A A 2 i )

³ i = 1

V 1^/.

^UB 1 = ₃E ( A B ( 2 i - 1 ) ⁺ A B 2 i ) ;

3 i = 1

V 1^/.

^UC = 7 E ( A C ( 2 i - 1 ) ⁺ A C 2 i );

³ i = 1

>

i A1 = 3

I _B i = ¹

B 1    3

i_c = ¹

C 3

3 A

^r i = ¹ v

A 2 i

—

A A ( 2 i - 1 ) + A B 2 i

^Z cAi

E ^f A B ²i - A ^{B ( 2 i - 1 )} = 1 V        Z cBi

E ^f A C ^{2 i} " A C ^{( 2 i - 1 )} = 1 V        Z cCi

—

A B ( 2 i - 1 ) + A C 2 i    A C ( 2 i - 1 )

Z cABi

Z cCAi

A A 2 i    A A ( 2 i - 1 )    A C 2 i A C ( 2 i - 1 )

Z cABi             Z cBCi      .

A A 2 i    A A ( 2 i - 1 )    A B 2 i    A B ( 2 i - 1 )

Z cCAi             Z cBCi      .

Уравнения (2) и (6) позволяют построить схему распределения амплитудных значений одной пары волн электромагнитного поля по линейному проводу A однородного участка ЛЭП однопроводного исполнения (рис. 1). По этим уравнениям и по схеме видно, что в каждом линейном проводе однородного участка трехпроводной ЛЭП присутствует 6 волн электромагнитного поля: 2 собственные и 4 наведенных от каждого соседнего линейного провода исследуемой ЛЭП.

Амплитуды волн электромагнитного поля характеризуются постоянными интегрирования. Постоянные интегрирования AA1 , AA3 , AA5 , AB1 , AB3 , AB5 , AC1 , AC3 и AC5 несут ответственность за отраженные волны, а постоянная интегрирования AA2 , AA4 , AA6 , AB2 , AB4 , AB6 , AC2 , AC4 и AC6 – за падающие. Причем величины постоянных интегрирования, ответственных за падающие волны электромагнитного поля, преобладают над величинами постоянных интегрирования, ответственных за отраженные волны.

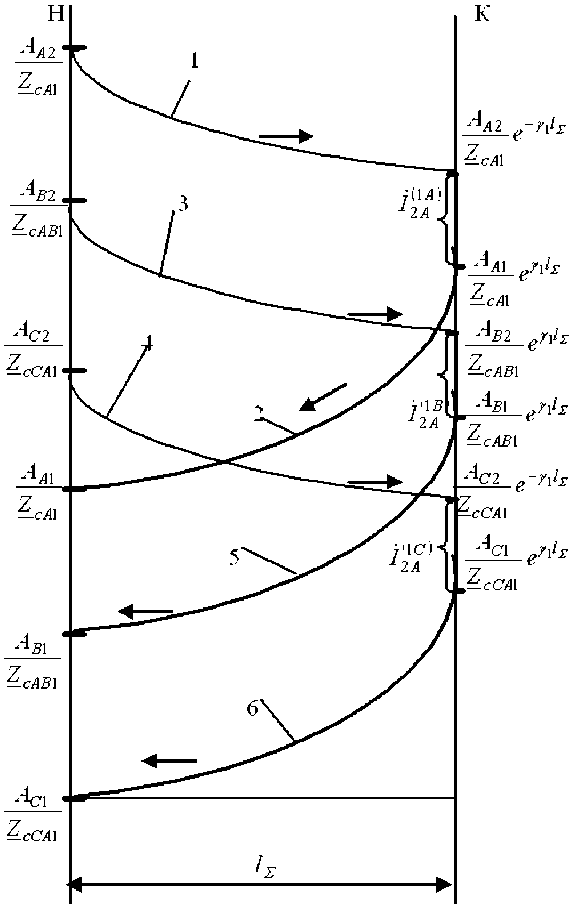
Рис. 1. Схема распределения амплитудных значений первой пары падающих и отраженных волн электромагнитного поля по линейному проводу А однородного участка трехфазной ЛЭП трехпроводного исполнения: 1 – собственная падающая волна; 2 – собственная отраженная волна; 3 – наведенная падающая волна от линейного провода В ; 4 – наведенная отраженная волна от линейного провода В ; 5 – наведенная падающая волна от линейного провода С ; 6 – наведенная отраженная волна от линейного провода С ; l _∑ – протяженность всего анализируемого участка ЛЭП

Для реализации уравнений (1)–(4) необходимы сведения о вторичных параметрах исследуемого однородного участка ЛЭП, а именно постоянных распространения волн электромагнитного поля по однородному участку, волновые сопротивления и постоянные интегрирования. Для определения вторичных параметров ЛЭП необходимо предварительно определить численные значения первичных параметров этого участка. Это можно сделать с помощью соответствующей справочной литературы [9, 10], аналитически [11–20] или экспериментально [20, 21]. И лишь после этого можно рассчитать постоянные распространения волн электромагнитного поля по токоведущим частям ЛЭП и соответствующие волновые сопротивления [4, 20].

Особое внимание следует обратить на методику определения численных значений постоянных интегрирования. Именно они совместно с постоянными распространения волн электромагнитного поля по линейным проводам ЛЭП и соответствующими волновыми сопротивлениями и определяют, судя по рис. 1, амплитудные значения падающих и отраженных волн. Эта методика определена для однородных участков ЛЭП элементарной (бесконечно малой) протяженности [4]. Но для анализа результатов передачи электрической энергии по ЛЭП конечной протяженности это не годится, поскольку в этом случае в многопроводных линиях электропередачи не учитывается электромагнитное воздействие линейных проводов друг на друга. Этот недостаток ликвидирован в [20]. Там представлена методика определения численных значений постоянных интегрирования с учетом электромагнитных связей между токоведущими частями ЛЭП. Такая методика применима для анализа передачи электрической энергии по ЛЭП конечной протяженности, но она очень громоздка. В предлагаемом исследовании предпринята попытка преодоления этого недостатка на основании схемы распределения волн электромагнитного поля по линейному проводу ЛЭП трехпроводного исполнения, изображенной на рис. 1.

Как известно, передача электрической энергии по каждому проводу однородного участка трехпроводного исполнения обеспечивается тремя парами волн электромагнитного поля. Для начала линейного провода А , судя по рис. 1, этот факт может быть представлен так:

-1f /⁽¹ ) /(2)    /²3П

1 1 A ^_ 3 ( 1 1 A ⁺ 1 1 A ⁺ 1 1 A ) ,

,(1) 22)       /(3)                                                          л где I1A , I1A и I1 A – доли тока в начале линии А от каждой пары волн электромагнитного поля.

Судя по уравнениям (2)–(4) и по схеме, изображенной на рис. 1, в каждом линейном проводе действуют токи от всех трех фаз от всех трех пар волн электромагнитного поля. Этот факт может быть обозначен следующим образом:

/ 2 1)_ / 2 ¹ A ), / 2 ¹ B ), i ( ^{1 C} ). 1 ¹ 1 A ^{_ 1} 1 A + ¹ 1 A + ¹ 1 A ;

/22) _ /22A). /22B). /22C).

>

¹ 1 A ^{_ 1} 1 A + ¹ 1 A + ¹ 1 A ; ’

/23) _ /23A) + j23B) + /23C)

11A _ 11A   + 11A   + 11A , где i2AA), I2 A) и IA A) - собственные токи в начале линейного провода А от первой, второй и третьей пар

X1B)   X 2 B)   ^3 B)     /21C)   /22 C)   /23 C)                                -                     л волн электромагнитного поля; I1A , I1A  , I1 A   и I1A , I1A , I1A   – токи в начале линейного провода А, наведенные от соседних проводов В и С от первой, второй и третьей пар волн электромагнитного поля.

Если уравнения (10) поместить в уравнение (9), то получится следующее:

/ -If /21 A) + /21 B) + /21C) + /22A) + /22 B) + /22 C) + /23A) + /23 B) + /23 C)

1 1 A ^_ 3 2 1 1 A ⁺ 1 1 A ⁺ 1 1 A ⁺ 1 1 A ⁺ 1 1 A ⁺ 1 1 A ⁺ 1 1 A ⁺ 1 1 A ⁺ 1 1 A ) •

Иначе эти соотношения можно записать так:

A A 2	- j21 AA^Z          ■ _ 1 1 A Z cA1 + A A1 ;	A B 2	= /2 1 B )7 1 1 A Z cAB 1	+ A B 1;	A C 2	_ I l A ZcCA1 + A C 1 ;
A A 4	_ /22 A _ 1 1 A   Z cA 2 + A A 3 ;	A B 4	_ /2 2 B ) 7 _ 1 1 A Z cAB 2	+ A B 3;	A C 4	- /22 C) 7     +     ' _ 1 1 A Z cCA 2 + A C 3 ;
A A 6	- i23AA^Z           ■ _ 1 1 A Z cA 3 + A A 5 ;	A B 6	- /2 3 B ) 7 _ 1 1 A Z cAB 3	+ A B 5;	A C 6	_ 1 1 A Z cCA 3 + A C 5 .

Из схемы распределения амплитудных значений волн электромагнитного поля по линейному проводу однородного участка ЛЭП трехпроводного исполнения (см. рис. 1) следует:

/ 2 1 A )	_ A A 2	A A1 .	/ 2 1 B )	A B 2 _	A B 1 .	/ 2 1 C )	A C 2 _	A C 1 .
I 1 A	Z cA 1	; Z cA 1	I 1 A	Z cAB 1	; Z cAB 1	I 1 A	Z cCA 1	; Z cCA 1
/ 2 2 A )	_ A A 4	A A 3 .	/ ( 2 B )	_ A B 4	A B 3 .	/ 2 2 C )	_ A C 4	A C 3
I 1 A	Z cA 2	; Z cA 2	I 1 A	Z cAB 2	; Z cAB 2	I 1 A	Z cCA 2	Z cCA 2
/ 2 3 A )	A A 6	A A 5 .	/ ( 3 B )	A B 6	A B 5 .	/ ( 3 C )	A C 6	A C 5
I 1 A	Z cA 3	; Z cA 3	I 1 A	Z cAB 3	; Z cAB 3	I 1 A	Z cCA 3	Z cCA 3

Чтобы реализовать эти соотношения, надо иметь сведения о численных значениях токов, входящих в их состав. В этой связи уместно вспомнить, что токи обратно пропорциональны соответствующим волновым сопротивлениям: ток i ^ AA ) обратно пропорционален собственному волновому сопротивлению Z _cA1 ; ток i ^ AB ) обратно пропорционален взаимному волновому сопротивлению Z _cAB1 ; ток I a ) - взаимному волновому сопротивлению Z cC_A1 ; ток I AA ) - собственному волновому сопротивлению Z _{cA 2} ; ток I AB ) -взаимному волновому сопротивлению Z cAB ₂ ; ток I ² 2C ) - взаимному волновому сопротивлению Z cCA ₂ ; ток I A A ) - собственному волновому сопротивлению Z cA ₃ ; ток l AB ) - взаимному волновому сопротивле- 2 3 C )

нию Z _{cAB 3} , а ток I _{1 A}  обратно пропорционален взаимному волновому сопротивлению Z _{cCA 3} . Но тогда

справедливо следующее: j21 A )     7       у 1 1 A       Z cA 2 7 1 .			/ 2 1 A ) I 1 A	Z cA 3	Y 1 ;	/ 2 1 B ) I 1 A	Z cAB 2	Y 1
/ 2 2 A ) I 1 A	Z cA 1	; Y 2	/ 2 3 A ) I 1 A	Z cA 1	Y3 ’	/ 2 2 B ) I 1 A	Z cAB 1	Y 2
/ 2 1 B ) I 1 A	Z cAB 3	Y 1 .	/ 2 1 C ) I 1 A	Z cCA 2	Y 1 ;	/ 2 1 C ) I 1 A	Z cCA 3	Y1 .
/ 2 3 B ) I 1 A	Z cAB 1	Y3 ’	/ 2 2 C ) I 1 A	Z cCA 1	Y2 ’	/ 2 3 C ) I 1 A	Z cCA 1	Y3 :

T ⁽¹ A )    7 _         7 7                    T⁽¹ A )     7 „         7 7

1 1 A _ Z cAB 1 _ Z 0 B Z 0 C   Z 0 BC   ;   1 1 A  _ Z cCA1 _ Z 0 B Z 0 C   Z 0 BC

T^{(1 B} )    Z_rAX    Z^caZ^-zZo4rZoc ⁷ T^(1C )    Z_rA\   Z_nn;Z(_U; -zZwaZm

I1A       cA1      0CA 0BC    0AB  0C    I1A        cA1      0 AB 0BC    0CA  0B где Z0B , Z0C , Z0AB , Z0BC и Z0CA – первичные параметры однородного участка ЛЭП трехпроводного исполнения [20].

Эти равенства позволят выразить все токи через ток ZA ) :

Т ( ² A ) _ ъ / ( 1 A )■

/ ⁽³ A ) _ У з / ⁽¹ A ).

I 1 A ^_      I 1 A ;

Y 1

I 1 A ^_      I 1 A ;

Y 1

/ ( 1 B ) _ Z 0 CA Z 0 BC

1 A

Z 0 B Z 0 C

—

Z 0 AB Z 0 C / ( 1 A ).

2          I 1 A ;

Z 0 BC

—

/ ( 2 B ) _ У 2 ⁽ Z 0 CA Z 0 BC "

¹ 1 A ^_        /

У 1 ( Z о B Z о с

—

Z 0 AB Z 0 C ) / ( 1 A ).

2           ^{1 A}

Z 0 BC )

/ ( ^{3 B} )

I _{1 A}

_ У з ⁽ Z 0 CA Z 0 BC

—

У 1 ( Z о B Z 0 с

Z 0 AB Z 0 C ) / ( 1 A ).

2           ^{1 A}

Z 0 BC )

/ ( 1 C ) _ Z 0 AB Z 0 BC "  1 A

Z 0 B Z 0 C

—

Z 0 CA Z 0 B / ( 1 A ).

2         I 1 A ;

Z 0 BC

—

/ ( 2 C )

I _{1 A}

_ У 2 ⁽ Z 0 AB Z 0 BC

—

У 1 ( Z о B Z о с

Z 0 CA Z 0 B ) / ( 1 A ).

2           ^{1 A}

Z 0 BC )

/ ( 3 C ) _ У 3 ⁽ Z 0 AB Z 0 BC "

¹ 1 A ^_       /

У 1 ( Z о B Z о с

—

Z 0 CA Z 0 B ) / ( 1 A )

2           ^{1 A}

Z 0 BC )

.

Если эти формулы подставить в уравнения (11), то получится уравнение с одним неизвестным, каковым в данном случае является ток /(AA). Его решение позволит определить формулу для вычисления этого тока:

/ (1 A ) ____________________________________

I 1 A ^_

^(y 1 ^{+ y} 2 ^{+ y} 3 ) ( Z 0 B Z 0 C

—

³ 1 1 A У 1 ( Z о B Z о с

Z 0 BC )

Z 0 BC ⁺ Z 0 CA Z 0 BC Z 0 AB Z 0 C ⁺ Z 0 AB Z 0 BC

—

Z 0 CA Z 0 B )

.

При подстановке в это уравнение равенств (12) в первое уравнение системы (5) с учетом формул (14) и (13) получается следующее:

Т

3U 1 A ^{_ 2} A A 1 ^{+ 2} A A 3 ^{+ 2} A A 5 ⁺

+---—

( Y 1 + Y 2 +Y 3 ) ( Z

Z 0 C

—

3 A I 1 A + 0

Z 0 BC ⁺ Z 0 CA Z 0 BC

—

Z 0 AB Z 0 C ⁺ Z 0 AB Z 0 BC

—

Z 0 CA Z 0 B )

_ 2 AA1 + 2 AA 3 + 2 AA 5 + a, где

^{A _} ( Z 0 B Z 0 C Z 2B 0 BC ) ^{( y} 1 Z cA 1 ^+Y 2 Z cA 2 ^{+ Y} 3 Z cA 3 ) •

Подобное рассуждение применительно и к линейным проводам В и С . В результате таких действий получаются уравнения: /

^{3 U} 1 B ^{_ 2} A B 1 ^{+ 2} A B 3 ^{+ 2} A B 5 ⁺

+_________________________________ 3 A I 1 B + 0 __________________________________

⁽У 1 +У 2 ^+Y 3 ) ( Z 0 A Z 0 C Z 0C 0 CA ⁺ Z 0 CA Z 0 BC ~ 0A 0 AB Z 0 C ⁺ Z 0 AB Z 0 CA ~ 0A 0 A Z 0 BC )

- ² A B 1 + ² A B ₃ + ² A B 5 + b ;                                                                         (16)

/

^{3 U} 1 C ^{_ 2} A C 1 ^{+ 2} A C 3 ^{+ 2} A C 5 ⁺

+_________________________________ 3 A I 1c + 0 __________________________________

⁽У 1 ^+y 2 ^+y 3 ) ( Z 0 A Z 0 B Z 0A 0 AB ⁺ Z 0 AB Z 0 BC Z 0C 0 CA Z 0 B ⁺ Z 0 AB Z 0 CA Z 0A 0 A Z 0 BC )

_ 2 A C 1 + 2 A C ₃ + 2 A C 5 + c .                                                                          (17)

Уравнения (15)–(17) образуют систему уравнений с девятью неизвестными. Для их совместного решения необходимо еще 6 уравнений. Их можно получить искусственно, используя производные уравнений (1) по переменной l . Вторую и четвертые производные.

Вторая производная первого уравнения системы (1) по переменной l имеет вид:

2/'t ddlUA _ 3 [y? (AA1 eY11 + AA2 e Y11 ) + Y2 (AA3 eY21 + AA4e Y21 ) + Y2 (AA5eY31 + AA6e Y31)] •

При условии l = 0 это уравнение примет вид:

2 ГГ

-21Ar = 3 ^[Y 1 ( A A1 + A A 2 ) + Y 2 ( A A 3 + A A 4 ) + Y 3 ( A A 5 + A A 6 ) ] ^.

С учетом формул (12), (13) и (14) это уравнение перепишется следующим образом:

Д ² IT       1

^ ₂^1Л = 3 ^[ 2 ^Y 1 A A 1 + 2 ^Y 2 A A 3 + 2 ^Y 3 A A 5 +

________________________________ ³ ^ I 1 a ( ^Y 2 + Y ² + Y 2 ) ________________________________ _

^(y 1 ^+y 2 ^+y 3 ) ( Z 0 B Z 0 C ^— Z 0 BC ⁺ Z 0 CA Z 0 BC ^— Z 0 AB Z 0 C ⁺ Z 0 AB Z 0 BC ^— Z 0 CA Z 0 B )

= 3 ( 2 ^Y 2 A A 1 ⁺ 2 ^Y 2 A A 3 ⁺ 2 ^Y 2 A A 5 ⁺ d ) .

Аналогично определяются вторые производные напряжений в начале линейных проводов В и С по переменной l :

d ² U _{1 B} dl ²

= 3 ^[ 2 ^Y 1 ^AB 1 ⁺ 2 ^Y 2 ^AB 3 ⁺ 2 ^Y 3 ^AB 5 ⁺

+

^{3 A I} 1 в ( y i^{2 +}Y ² + Y 2 )

' 1 +^Y 2 +^Y 3 ) ( Z о A Z 0 C ^— Z 0 CA ⁺ Z 0 CA Z 0 BC ^— Z 0 AB Z 0 C ⁺ Z 0 AB Z 0 CA ^— Z 0 A Z 0 BC

= 3 ( 2 ^Y 1 A B 1 ⁺ 2 ^Y 2 A B 3 ⁺ 2 ^Y 3 A B 5 ⁺ f ) ;

dUT = ^{1 [} 2 Y 2 A c 1 ^{+ 2} Y 2 A c 3 ⁺ 2 Y 32 A c 5 ⁺ dl ²      3

^{3 A I} 1 c ( Y 2 +Y 2 +Y 2 )

' 1 ^{+ Y} 2 ^{+ Y} 3 ) ( Z 0 A Z 0 B ^— Z 0 AB ⁺ Z 0 AB Z 0 BC ^— Z 0 CA Z 0 B ⁺⁺ Z 0 AB Z 0 CA ^— Z 0 A Z 0 BC

= 3 ( 2 ^ 2 A C 1 ^{+ 2 Y} 2 A C 3 ^{+ 3 Y 3} A C 5 ⁺ g ) .

Иначе вторые производные напряжений в начале линейных проводов однородного участка ЛЭП трехпроводного исполнения можно выразить через первичные параметры анализируемого участка ЛЭП следующим образом [20]:

d2 U d 2A = ( Z 0 AY 0 A 0 + Z 0 AY 0 AB + Z 0 AY 0 CA — Z 0 ABY 0 AB

—

Z 0 CA Y 0 CA ) ^U 1 A

—

Z 0 A Y 0 AB Z 0 AB Y 0 B 0 Z 0 AB Y 0 BC Z 0 AB Y 0 AB ⁺ Z 0 CA Y 0 BC ) ^U 1 B

Z 0 A Y 0 CA ⁺ Z 0 AB Y 0 BC ^— Z 0 CA Y 0 C 0 ^— Z 0 CA Y 0 CA ^— Z 0 CA Y 0 BC ) ^U 1 C = D ;

A 2 Л d U1B dl 2    ( Z 0 B Y 0 B 0 + Z 0 B Y 0 BC + Z 0 B Y 0 AB

—

Z 0 AB Y 0 AB

—

Z 0 BC Y 0 BC ) ^U 1 B

—

—

⁽ Z 0 B Y 0 AB

—

Z 0 AB Y 0 A 0

—

Z 0 AB Y 0 AB

—

Z 0 AB Y 0 CA ⁺ Z 0 BC Y 0 CA ) ^U 1 A

—

—

⁽ Z 0 B Y 0 BC ⁺ Z 0 AB Y 0 CA

—

Z 0 BC Y 0 C 0

—

Z 0 BC Y 0 CA

—

Z 0 BC Y 0 BC ) ^U 1 C = E ;

dи С

-"^i  = ⁽ Z 0 C Y 0 С 0 ⁺ Z 0 C Y 0 CA ⁺ Z 0 C Y 0 BC ^— Z 0 CA Y 0 CA

—

Z 0 BC Y 0 BC ) ^U 1 C

—

—

⁽ Z 0 C Y 0 CA

—

Z 0 AB Y 0 A 0

—

Z 0 AB Y 0 AB Z 0 AB Y 0 CA ⁺ Z 0 BC Y 0 AB ) ^U 1 A

—

—

⁽ Z 0 C Y 0 BC ⁺ Z 0 AB Y 0 AB

—

Z 0 BC Y 0 B 0 Z 0 BC Y 0 BC

—

Z 0 BC Y 0 AB ) ^U 1 B = F .

Если совместить эти уравнения с уравнениями (18)–(20), то получится следующее:

3 ( 2 y 2 A A1 + 2 y 2 a a 3 + 2 Y 2 a a 5 + d ) = D ;

3 ( 2 y 2 A bi + 2 y 2 A b з + 2 y 2 A b 5 + f ) = E ; .

3 ( 2 ^Y 2 A c 1 ⁺ 2 ^Y 2 A c 3 ⁺ 2 У з A c 5 ⁺ g ) = F •

Четвертая производная напряжения в линии А по переменной l может быть представлена в следующем виде:

' A = 3 [y 4 ( A a i e ^{Y 1} l + A a 2 e   ) + y 4 ( a a 3 e ^Y 2 l + a a 4 e ^—Y 2 l ) +y 4 ( a a 5 e ^{Y 3} l + a a 6 e ^³ l ) ] .

Для начала линейного провода А при условии l = 0 это уравнение с учетом равенств (12) и (13) после ряда преобразований получается перепишется так:

я 4т Т1 -

^ 4' = 3 ^[ 2 ^Y 1 A A1 ^{+ 2 y} 2 A A 3 ^{+ 2 y} 3 A A 5 ⁺

+

____________________________ 3 A I 1 A ( Y 4 +Y 4 +Y 4 ) _____________________________

' 1 ^{+ y} 2 ^{+ y} 3 ) ( Z 0 B Z 0 C - Z 0 BC ⁺ Z 0 CA Z 0 BC ^— Z 0 AB Z 0 C ⁺ Z 0 AB Z 0 BC ^— Z 0 CA Z 0 B

= 3 (2 Y4 Aai + 2Y4 Aa 3 + 2Y4 aa 5 + h).(22)

Аналогично определяются четвертые производные напряжений в начале других линейных проводов:

4 т

P =y[2Y1 AB 1 + 2Y2 AB 3 + 2Y3 AB 5 + dl4

____________________________ 3A i 1 B ( y 4 +y 4 +y 4 ) _____________________________ ' 1 + ^Y 2 + ^Y 3 ) ( Z 0 A Z 0 C ^— Z 0 CA ⁺ Z 0 CA Z 0 BC ^— Z 0 AB Z 0 C ⁺ Z 0 AB Z 0 CA ^— Z 0 A Z 0 BC

= 3 ( 2 ^Y 1 A b 1 ⁺ 2 ^Y 2 A b 3 ⁺ 2 ^Y 3 A b 5 ⁺ k ) ^;

d 4 U J xc dl ⁴

= 3 ^[ 2 ^Y 1 A C 1 ⁺ 2 ^Y 2 A C 3 ⁺ 2 ^Y 3 A C 5 ⁺

+

3 A I 1 C ( y 4 + y 4 + y 4 )

Z 0 B

Z 0 AB ⁺ Z 0 AB Z 0 BC

-

Z 0 CA Z 0 B ⁺ Z 0 AB Z 0 CA

-

Z 0 A Z 0 BC )

= 3 ( 2 ^Y 1 A C 1 ⁺ 2 ^Y 2 A C 3 ⁺ 2 ^Y 3 A C 5 ⁺ m ) .

Иначе эти производные можно представить так:

dl 4 A = ⁽ Z 0 A Y 0 A 0 ⁺ Z 0 A Y 0 AB ⁺ Z 0 A Y 0 CA ^— Z 0 AB Y 0 AB

—

Z 0 CA Y 0 CA ) D

—

—

⁽ Z 0 A ^Y 0 AB

—

Z 0 AB Y 0 B 0

—

Z 0 AB ^Y 0 BC Z 0 AB Y 0 AB ⁺ Z 0 CA Y 0 BC ) E

—

—

⁽ Z 0 A Y 0 CA ⁺ Z 0 AB Y 0 BC

—

Z 0 CA Y 0 C 0

—

Z 0 CA Y 0 CA

—

Z 0 CA Y 0 BC ) F = G ;

d ² U _{1 B} dl ⁴

= ⁽ Z 0 B Y 0 B 0 ⁺ Z 0 B Y 0 BC

⁺ Z 0 B Y 0 AB

Z 0 AB ^Y 0 AB

Z 0 BC Y 0 BC ) E

Z 0 B Y 0 AB Z 0 AB Y 0 A 0 Z 0 AB Y 0 AB Z 0 AB Y 0 CA ⁺ Z 0 BC Y 0 CA ) D

Z 0 B Y 0 BC ⁺ Z 0 AB Y 0 CA Z- 0 BC Y 0 C 0 Z 0 BC Y 0 CA Z 0 BC Y 0 BC ) F = H ;

d4Ulcc       v 7 v 7 v dl4 =(Z0cY0c0 + Z0c Y0CA + Z0c Y0BC

—

Z 0 CA Y 0 CA

—

Z 0 BC Y 0 BC ) F

—

Z 0 C Y 0 CA Z 0 AB Y 0 A 0 Z 0 AB Y 0 AB Z 0 AB Y 0 CA ⁺ Z 0 BC Y 0 AB ) D

Z 0 C Y 0 BC ⁺ Z 0 AB Y 0 AB Z 0B 0 BC Y 0 B 0 ^— Z 0 BC Y 0 BC ^Z0B 0 BC Y 0 AB ) E = J .

Объединение этих уравнений с уравнениями (22)–(24) позволит получить следующее:

3 ( 2 y 4 A ai + 2 y 4 A.

3 ( 2 y 4 A bi + 2 y 4 A

I A 3 + 2 Y 4 A A 5 + h ) = G ;

*B 3 ⁺ 2 ^Y 3 A B 5 ⁺ k ) = H ;

3 ( 2 ^Y 1 A C 1 ⁺ 2 ^Y 2 A C 3 ⁺ 2 ^Y 3 A C 5 ⁺ m ) = J .

Совместное решение уравнений (15)–(17), (21) и (25) позволит сформировать формулы для вычисления постоянных интегрирования A _{A 1} , A _{A 3} , A _{A 5} , A _{B 1} , A _{B 3} , A _{B 5} , A _{C 1} , A _{C 3} и A _{C 5} :

3 G - 3 D ( y ² + Y 2 ) + 3 y ² Y 32 U A — a Y 2 Y 2 + d ( y 2 + Y 2 ) - h 2 Y 4 ^- 2 Y 1 ( y ² + Y 2 ) ⁺ 2 Y ² Y 3²

3 D — 2 A A 1 ( y i —Y 2 ) — 3 y | U A + a Y 2

- d

2 (y 2-y2 )

.  - 3U 1 A — a _л л

A A 5 =     2      A A 1 - A A 3 ;

M^^ E ^llljWl^

B 1                   2 Y 4 - 2 y i ( y ² + Y 3 ) ^{+ 2} Y ² Y 3²

_ 3 E - 2 A b 1 ( y i -Y 3 ² ) — 3 Y 2 U 7 i в + b Y 2 — f

A b 3 =

² ( y ^{2 -}Y 2 )

.   _ 3U 1 в - b .      .

A B 5 =---Z-- A B 1 ^- A B 3;

A _{C 1}

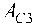
³ J ^{- 3} F ( y ^{2 +} Y 3² ) ^{+ 3} Y ² Y 3^U1C ^- c Y ² Y 3^{2 +} g ( y ^{2 +} Y 3² ) ^- m 2 Y 4 ^{- 2} Y 1 ( y ² +Y 2 ) ⁺ 2 Y ² Y 3²

³ F ^{- 2} A c 1 (Y 1 ^-Y 3 )^{- 3} Y 2 U 7 1 C ⁺ c Y ^{2 -} g 2[?М

Л - ^3U 1 C ^- c л л A C 5 =--- 2 A C 1 ^- A C 3 .

Постоянные интегрирования A _{A 2} , A _{A 4} , A _{A 6} , A _{B 2} , A _{B 4} , A _{B 6} , A _{C 2} , A _{C 4} и A _{C 6} вычисляются по формулам (12).

Постоянные интегрирования совместно с постоянными распространения волн электромагнитного поля по линейным проводам ЛЭП и соответствующими волновыми сопротивлениями, судя по рис. 1, определяют амплитуды падающих и отраженных волн на всей протяженности однородного участка линии электропередачи трехпроводного исполнения. Кроме того, численные значения этих величин дают реальную возможность прогнозирования напряжений и токов на однородном участке трехпроводной ЛЭП по формулам (1)–(4). Но для этого необходимо иметь достоверные сведения не только о численных значениях первичных параметров анализируемого участка трехфазной ЛЭП, но и о численных значениях входных напряжений и токов. Графическая интерпретация результатов такого прогнозирования приведена на рис. 2 и 3. Здесь показана графическая интерпретация распределения фазного напряжения и линейного тока по однородному участку ЛЭП-220 кВ трехпроводного исполнения на частоте 13-й гармонической составляющей. Этими интерпретациями подтверждается волновой характер распределения напряжений и токов по проводам ЛЭП трехпроводного исполнения со сравнительно небольшой длиной волны [20].

Прогнозирование напряжений и токов при пониженном качестве электрической энергии следует выполнять для каждой гармонической составляющей. А чтобы иметь представление обо всем напряжении и обо всем токе, полученные таким образом данные следует обобщить на весь спектр основных характеристик электрической энергии.

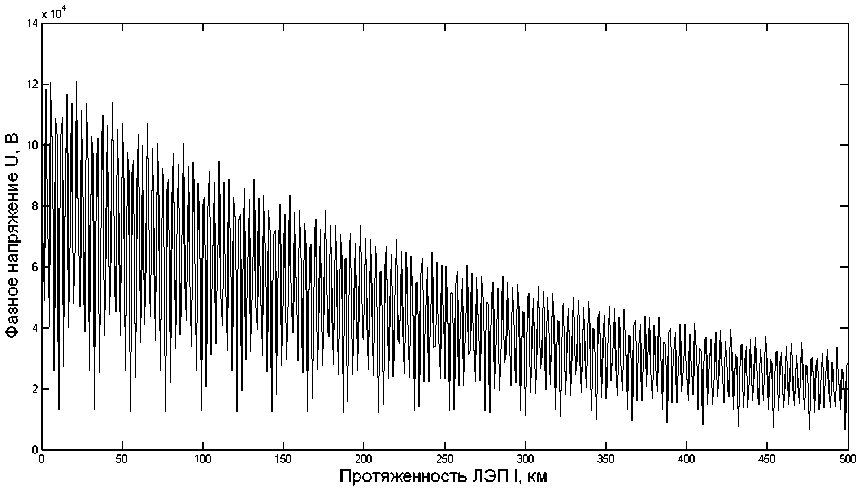
Рис. 2. Графическая интерпретация распределения фазного напряжения на частоте 13-й гармонической составляющей по однородному участку ЛЭП трехпроводного исполнения

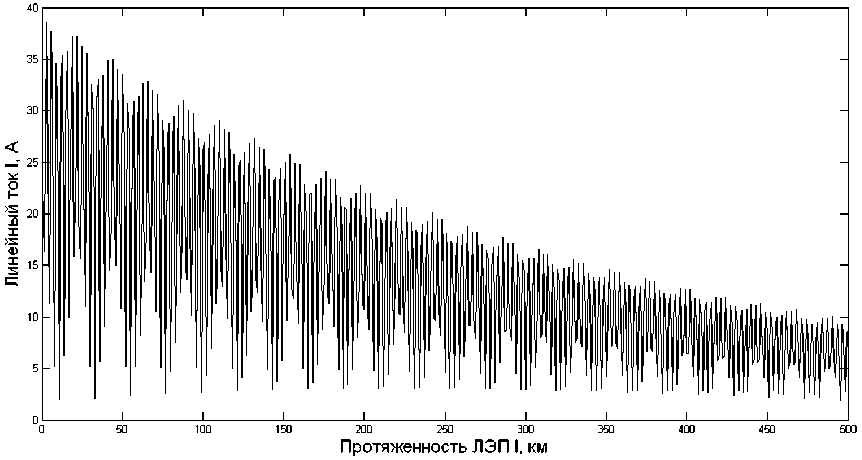
Рис. 3. Графическая интерпретация распределения линейного тока на частоте 13-й гармонической составляющей по однородному участку ЛЭП трехпроводного исполнения

Разработана методика определения численных значений постоянных интегрирования, необходимых для прогнозирования напряжений и токов на однородном участке ЛЭП трехпроводного исполнения. Постоянные интегрирования вместе c постоянными распространения волн электромагнитного поля и волновыми сопротивлениями позволят получить сведения об амплитудных значениях падающих и отраженных волн, обеспечивающих передачу электрической энергии по однородному участку трехпроводной линии электропередачи. Общее представление об амплитудах этих волн позволит получить схема их распределения по линейному проводу исследуемой ЛЭП, изображенная на рис. 1, или графические интерпретации распределения фазного напряжения.

Результаты описываемого здесь исследования могут быть использованы на стадии проектирования, реконструкции и эксплуатации ЛЭП трехпроводного исполнения напряжением 220 кВ и выше протяженностью более 200 км для прогнозирования напряжений и токов на различных участках линии электропередачи. А при пониженном каче- стве электрической энергии предлагаемая методика может быть использована и при анализе функционирования ЛЭП напряжением 35 кВ и выше протяженностью несколько десятков километров и более.

Прогнозирование амплитудных значений падающих и отраженных волн электромагнитного поля в линейных проводах двухцепной ЛЭП позволит детально проанализировать напряжения и токи на однородном участке линии электропередачи. Этот факт позволит разработать наиболее приемлемые способы оптимизации передачи электрической энергии. Причем применение предлагаемой методики возможно и в условиях пониженного качества электрической энергии. В этом случае все расчеты выполняются для каждой гармонической составляющей напряжения и тока с последующим обобщением полученных результатов на весь спектр основных характеристик электрической энергии.