An Algebraic Method for the N-Queens Problem Based on Permutation Operation Group

Published Online April 2011 in MECS

This paper will give some novel results by analyzing solutions of N-Queens problem based on permutation space. The analyses integrate geometric approaches, such as dihedral group D 4 , and algebraic approaches, such as group action, isomorphism, orbit and generator, but main contributions of this paper are presented in algebraic form. The remainder of this paper is organized as follows. To analyze permutations as solutions of N-Queens problem, this paper firstly defines isomorphic operations of D 4 in permutation spaces in section 2. By these operations, other solutions isomorphic to an existing solution can be obtained easily. Except operations among elements within an orbit, Section 3 proposes two operators to generate new orbits from existing orbits. Section 4 presents a method to distinguish a newly generated orbit from the existing one by the concept of orbit signature. Section 5 gives an algorithm to search solutions based on orbit signature, also an example as the application of the algorithm is presented.

П Permutation Operation Group PO and its ISOMORPHIC MAP

For a permutation   ^{1    2 ..., i ,...    N} ,  briefly

P              (P1  P2  ..., Pp-  Pn ) , J marked as (p1, p2,…, pi,…, pN) in the following, pi is row index of a queen in column , and p1p2…pi…pn is an arrangement of the sequence from 1 to N. Sometimes pi is called permutation element, permutation subscript. The inherent advantages to represent solutions as permutations lie in that collisions of queens from the same row or the same column can never occur, and the only thing to do is to check whether there are diagonal collisions of queens. Diagonal collisions include attacks on positive diagonal (or sum diagonal) and negative diagonal (or difference diagonal), both of them can be expressed as follows (1):

(p i^- p j) *(p i^- p j ) * ⁽ i ^- j )*( i ^- j ), i * j .                  ⁽¹⁾

When a permutation is qualified as solution of N-Queens problem, can it be used to generate other solutions? A geometric thinking will solve this question.

For a N x N chessboard, any non-attacking layout of queens in the board can be exerted some geometric symmetric transformations to produce other layouts, which are qualified as solutions of N-Queens problem too. These geometric transformations form Dihedral group D 4 [17]. Eight elements of D 4 include: g 1 (identity map), g 2 (reflection along negative diagonal), g 3 (reflection along positive diagonal), g 4 (vertical reflection along horizontal center line), g 5 (horizontal reflection along vertical center line), g 6 (rotation through П /2), g 7 (rotation through П ), g 8 (rotation through 3n/2). All rotations mentioned here are counterclockwise. Generally speaking, fixed points under all these 8 transformation are very few. So for most cases, obtaining one layout of queens means getting at most eight solutions simultaneously.

To analyze N-Queens problem in permutation space, some permutation operations similar to transformations in D 4 must be found. The following will define three basic permutation operations first, then give all the eight operations corresponding to eight symmetric elements of D 4 , finally discuss the isomorphism of permutation operation and D 4 .

Three basic permutation operations are defined as follows.

(1)Define operation Inv ( p ) to get inverse of permutation p . The operation swaps every element p i with its subscript i of p firstly, then sorts new permutation elements by its new subscript ascending. The following example illustrates computation of inverse operation Inv .

12345  13524  12345

( 13 5 2 4 ) ^ ( 1 2 3 4 5 ) ^ ( 1 4 2 5 3 )

(2)Define operation Cmpl ( p ) to get complement of permutation p , the complement is based on N +1. For every element p i of p , substitute it with value N +1- p i . The following example illustrates computation of complement operation Cmpl .

12345    1   2   3   4   5

( 1 3 5 2 4 ) ^ ( 6 - 1 6 - 3 6 - 5 6 - 2 6 - 4 ) ^ 12345 ( 5 3 1 4 2 )

(3)Define operation Rev ( p ) to get reverse of permutation p . The operation just reverses all elements p i of p . The following example illustrates computation of reverse operation Rev .

12345  12345

( 1 3 5 2 4 ) ^ ( 4 2 5 3 1 )

Multiplication of these three operations complies with the composition rule. Obviously, for operation Inv ,

Cmpl and Rev , twice consecutive operations will make a permutation revert, that is to say, when f refers to one of them, p any permutation, there exists f ² ( p )= p .

Based on the three basic permutation operations, the eight operations for permutation can be defined following symmetric operations g i (i=1, 2,…, 8) of D 4 , they are denoted in the form of po i (i =1, 2,…, 8).

(1)For identity map g 1 , the identity permutation e (1, 2, 3,…, N ) is just the identity operation po 1 of permutation, for any permutation p , po 1 ( p )= e ( p )= p .

(2)For reflection g 2 , the equivalent permutation operation po 2 is Inv , the operation to get inverse of a permutation, for any permutation p , po 2 ( p )= Inv ( p ).

(3)For vertical reflection g 4 , the equivalent permutation operation po 4 is Cmpl , the operation to get complement of a permutation, for any permutation p , po 4 ( p )= Cmpl ( p ).

(4)For horizontal reflection g 5 , the equivalent permutation operation po 5 is Rev , the operation to get reverse of a permutation, for any permutation p , po 5 ( p )= Rev ( p ).

(5)For reflection g 3 , the equivalent permutation operation po 3 can be obtained by applying po 2 firstly, then applying po 4 , finally po 5 , for any permutation p , po 3 (p)= Rev ( Cmpl ( Inv ( p ))).

(6)For rotation g 6 , its equivalent permutation operation po 6 can be obtained by applying po 2 firstly, then applying po 4 , for any permutation p , po 6 ( p )= Cmpl ( Inv ( p )).

(7)For rotation g 7 , its equivalent permutation operation po 7 can be obtained by applying po 4 and po 5 successively by any sequence due to commutatively of them, for example, for any permutation p , po 7 ( p )= Rev ( Cmpl ( p )).

(8)For rotation g 8 , its equivalent permutation operation po 8 can be obtained by applying po 4 firstly, then applying po 2 , for any permutation p , po 8 ( p )= Inv ( Cmpl ( p )).

In fact, most of the operations can be implemented by reusing other operations, such as po 6 ( p )= Cmpl(po 2 ), po 3 ( p )= Rev(po 6 ), po 7 ( p )= Rev(po 4 ), po 8 ( p )= Inv(po 4 ).

Multiplication of any two permutation operations is given as Table 1.

Table 1: Multiplication of permutation operations (elements of PO )

	po 1	po 2	po 3	po 4	po 5	po 6	po 7	po 8
po 1	po 1	po 2	po 3	po 4	po 5	po 6	po 7	po 8
po 2	po 2	po 1	po 7	po 6	po 8	po 4	po 3	po 5
po 3	po 3	po 7	po 1	po 8	po 6	po 5	po 2	po 4
po 4	po 4	po 8	po 6	po 1	po 7	po 3	po 5	po 2
po 5	po 5	po 6	po 8	po 7	po 1	po 2	po 4	po 3
po 6	po 6	po 5	po 4	po 2	po 3	po 7	po 8	po 1
po 7	po 7	po 3	po 2	po 5	po 4	po 8	po 1	po 6
po 8	po 8	po 4	po 5	po 3	po 2	po 1	po 6	po 7

It can be verified that permutation operation poi(i=1, 2,…, 8) satisfies four axioms of group, so they form a group, denoted by Permutation Operation Group PO. (1)Closure. It is clear that product of any two elements poi and poj of PO still lies in the set, so multiplication of any two elements from PO is close. (2) Associatively. For any three elements poi, poj and pok (not necessarily distinct) of PO, (poi poj) pok = poi (poj pok). (3) Identity. The element po1 is just the one. For any element poi of PO, poi po1 = poi = po1 poi. (4) Inevitability. Inverse of identity element po1 is itself. For reflection operation, inverse of poi (i=2, 3, 4, 5) is themselves respectively. For rotational operation, po6po8=po1, po7 po7=po1, so po6-1=po8, po8-1=po6, and po7-1=po7. So inverse of element poi still belongs to PO.

From definitions of permutation operations, it can be inferred that D 4 and PO are isomorphic groups. Define the map g i ^ po _i (i=1,2,^,8), and denote the map as Ip: D 4 ^ PO . Clearly, map Ip is bijection. Define the combination manner of elements from D 4 and PO : if g ^ Po i , g j ^ Po j , ^then gg j ^ PoPo j . So ^{p (} gg j )= PoPo j = ^{p (} g i ) P( g j ), for all g _i , g j e D 4 . Thus D 4 and PO are isomorphic groups.

Isomorphism of D 4 and PO ensures completeness of permutation operations. For N-Queens problem, all solutions are in the form of permutation, so group PO is the right tool to operate on permutation space. When a solution is found, action of PO on it will generate some other solutions. Moreover, from points of view of group action, these solutions are on the same orbit, and the first solution is generator of the orbit. So action of PO will find all elements on an orbit.

Ш Orbit Operations to generate new orbits

Permutation operation group PO generates all elements on an orbit from the generator, which means finding a solution equals finding the orbit, and altering an element on an orbit equals altering the orbit, so discussions can be focused on orbit space rather than permutation space. To operate on the orbit, some orbit operations must be defined on orbit space. The following will reach this by defining two operators. One is Inc , the operator to upgrade an orbit by increasing a queen to permutations of order N so as to get solutions of order N +1. The other is Mov , the operator to transmute an orbit by moving a queen within a permutation to get another solution. Both upgrade operation and transmutation operation should assure integrity of a permutation as the solution of N-Queens problem.

• A.    Definition of operator Inc

The operator Inc is defined to upgrade an orbit by increasing a queen to an solution, and its usage form is Inc ( Row , Col ), where Row and Col , the permutation element and permutation subscript respectively, indicate the position to place the new queen.

First discussions go to these two parameters. To avoid collision with existing queens, new columns can’t be those existing ones. So the column to be added should be a virtual value between two columns, It is done by expressing Col in the form of a fraction with 0.5, and the newly generated column will be Col+0.5. For example, column 4.5 indicates that a new column will be added between column 4 and column 5, and that the new column will be column 5 if added successfully. By that means, column 0.5 indicates the left most column and the forthcoming column 1, and column 5.5 for N=5 indicates the right most column and a will-be column 6. The similar discussions apply to parameter Row.

The operation Inc ( Row , Col ) can be decomposed into two actions denoted by IncRow ( Row ), to increase a new row marked as Row , and IncCol ( Col ), to increase a new column marked as Col . Separately, when implementing IncRow ( Row ), all rows bigger than Row , i.e. permutation elements between ( Row , N ], should be added 1. And when implementing IncCol ( Col ), all columns bigger than Col , i.e. permutation subscripts between ( Col , N ], should be added 1. However, to keep integrity of a solution, operation IncRow must accompany operation IncCol and vice versa. So operation Inc ( Row , Col ) should be done as follows: firstly apply operation IncRow ( Row ) to increase permutation elements in the range of ( Row , N ] by 1, secondly apply operation IncCol ( Col ) to increase permutation subscript in the range of ( Col , N ] by 1, then fill the blank position of permutation subscript Col +0.5 with a value Row +0.5 indicating the position of the newly added queen.

Some examples are given as follows to illustrate operation Inc . All of them increase a queen to the solution (2, 4, 1, 3) of N =4, and generate a solution of N =5.

• (1)    Inc (0.5, 0.5) : increase a queen on the top l eft.

1 2 3 4                            1 2 3 4               1 2 3 4 5

( 2 4 1 3 ) t i n i ninul r гишшшиг ( 3 5 2 4 ) t i nn u iml r ( 1 3 5 2 4 )

• (2)    Inc (4.5, 4.5): increase a queen on the bottom right corner.

1 2 3 4                              1 2 3 4                1 2 3 4 5

( 2 4 1 3 ) fflfflnri tu ti ⁵) (ll‘riV o li ¹4 i ii¹ ( 2 4 1 3 ) ЯПШПй! ( 2 4 1 3 5 )

• (3)    Inc (0.5, 4.5): increase a queen on the top right corner.

(4) Inc (4.5, 0.5): increase a queen on the bottom left corner.

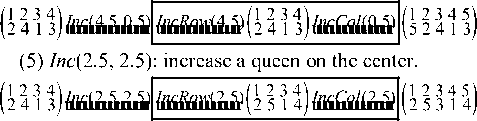
• B.    Definition of operator Mov

The operator Mov is defined to transmute an orbit by moving a queen within a solution, and its usage form is Mov ( OldRow , OldCol , NewRow , NewCol ), where ( OldRow , OldCol ) is the old position of the queen, ( NewRow , NewCol ) the new position. Note that for order N , values of NewRow and NewCol are virtual positions, but OldRow and OldCol are real position, and all of them are uniformly marked as the value before any changes to row and column. The operation can be done by two steps: to delete the queen at ( OldRow , OldCol ), to add a queen to ( NewRow , NewCol ).

To delete a queen, define operation Del ( Row , Col ) to do something contrary to operation Inc ( Row , Col ). The Operation can be done by two steps: to delete the queen from row by operation DelRow ( Row ), and to delete it from column by operation DelCol ( Col ). The three operators Del , DelRow , and DelCol can be defined following Inc , IncRow , IncCol . To realize DelRow ( Row ), decrease all permutation elements in the range of ( Row , N ] by 1. To realize DelCol ( Col ), first to remove permutation element at subscript Col , then decrease all permutation subscripts remained in the range of ( Col , N ] by 1. To realize Del ( Row , Col ), use DelRow ( Row ) firstly, DelCol ( Col ) secondly. The final result is that a solution of order N is changed to the solution of order N -1. The following example illustrates the operation of Del to delete a queen from the solution of N =5 to get a solution of N =4.

1 2 3 4 5                         1 2 3 4 5              1 2 3 4

( 2 5 3 1 4 ) D llltlll De l Rw ll ( 2 4 3 1 3 ) D ll Co llll ( 2 4 1 3 )

With operator Inc and Del , the operator Mov can be achieved easily. However, considering the relationship of new position ( NewRow , NewCol ) and old position ( OldRow , OldCol ), more attention should be paid to the sequence to do Inc ( NewRow , NewCol ) and Del ( OldRow , OldCol ), otherwise wrong modification of row and column by the former operation certainly results in a wrong parameter which definitely induces the latter operation to go wrong. Some useful tips are that the former operation should impact as less as possible on the position for the latter operation. The following examples give some explanations.

(1)to fulfill Mov (1, 1, 3.5, 3.5) within the solution (1, 3, 5, 2, 4) of N =5, perform Inc (3.5, 3.5) firstly, Del (1, 1) secondly.

________(1 3 5 2 4) Millllliili5l3l5)

1 2 3 4 5 6           1 2 3 4 5

rnl i iiinm l ( 1 3 6 4 2 5 ) D ll tie l ( 2 5 3 1 4 )

(2)to fulfill Mov (5, 5, 3.5, 3.5) within the solution (2, 4, 1, 7, 5, 3, 6) of N =7, perform Del (5, 5) firstly, Inc (3.5, 3.5) secondly.

1 2 3 4 5 6 7

( 2 4 1 7 5 3 6 ) MV ilh5ii ⁵ ii ³i 5ii³ii5 l

1 2 3 4 5 6                1 2 3 4 5 6 7

l ( 2 4 1 6 3 5 ) l i Uteehitil ( 2 5 1 4 7 3 6 )

IV Orbit Signatures

To identify an orbit, it means to give it a signature. Requirements of orbit signature include: (1) Uniqueness. For any order N , no orbit will have a duplicate signature. The Map from an orbit to its signature is a bijection. (2) Coincidence. Every solution on one orbit has identical structure, and the signature is a description of the inherent property, so every solution on the orbit should have unanimous value, which is used as orbit signature. (3) Easy-computation. For efficiency of search, calculation of orbit signature should be easily done, and some compromise on computation should be allowed.

To describe orbit inherence by its elements, which are obtained by operations similar to symmetric transformations, something invariant under these geometric operations must be found. A second thinking on D 4 will find that such transformations as reflections and rotations are all orthogonal, whose invariants include the distance between two points and the included angle between two sides formed by three points. For computing convenience, the included angle for two sides is substituted by the area of the three points. So distance and area are ideal parameters to depict internal structure of a geometric figure.

In any solution, every three adjacent queens construct a triangle. The signature of a triangle Sig - is defined as a Length - Area -triple as (2)

Sig - =(Length S1de1, Area । Length ^2) (2) where side1 and side2 are any two adjacent sides of the triangle, and Lengthside1 and Lengthside2 are their length respectively, and Area is the area of the triangle. For a triangle formed by three points a(xa, ya), b(xb, yb), and c(xc, yc), the length of side ab is computed in (3), and the area of the triangle is computed in (4). A little deviation of length and area from their common definition is to leave them as integers for computing simplicity.

Length ( ab )=( x a - x b ) x ( x _a - x b )+( y a - y _b ) x ( y a - y _b )       (3)

Area ( abc )=

xa xb xc

ya yb yc

1| =|( x a - x b ) x ( y c - y b )-( x c - x b ) x (y a - y b )|

(4) Clearly, if the signature of two triangles is the same, they are equivalent.

In a solution of order N , all queens form N -2 adjacent triangles. As for a set of N triangles, its signature Sig - _s is defined as (5).

Sig - s ={ Sig - i |i=1| 2|^i N} (5)

For any layout shown in fig. 1(a), there are two ways to form adjacent triangles. One is along x directions in fig. 1(b), by which any three points with continuous x value form a triangle. The other is along y directions in fig. 1(c), by which any three points with continuous y value form a triangle. These two ways give respectively two signatures, Sig - _x and Sig - y . Define the signature of a solution as (6).

Sig s ={ Sig - x i Sig - y } (6)

□□□□■□□□□

□□□□□□□□■

□□■□□□□□□

□□□□□□□■□

• (a) the layout of a solution

  

  (b) along x direction

  
  
  

  (c) along y

  direction

  
  

fig. 1 Computation of a solution’s signature

In permutation space, for any permutation p , the pair of permutation elements p i and its subscript i , ( i , p i ), is arranged by i ascendingly, so this form is fit for computing Sig - x , denoted as Sig _px here. According to definitions of (2) - (5), Sig px of permutation p is calculated as (7).

Sig px ={(1+( p i+1 - p i ) ² , | p i+2 -2 p i+1 + p i |, 1+( p i+2 - p i+1 ) ² )|i=1,

2,…, N -2} (7) To calculate Sig - y , denoted as Sig py here, it is necessary to get the pair ( i , p i ) arranged by p i ascendingly, which means to get inverse of p , so there exist (8)

Sig _py = Sig_Inv (_p)_x (8)

By (7) and (8), the signature Sig p of permutation p is calculated as (9).

Sig p ={ Sig px , Sig py } (9)

Due to effects of symmetric transformations, there are sequential differences within the signatures of two permutations on the same orbit. So comparing criterion must be defined to recognize the same signatures of the orbit, it is Sequential-Reverse criterion.

(1)For two signatures Sig - 1 ( Length 11 , Area 1 , Length 21 ) and Sig - ₂ ( Length 12 , Area 2 , Length 22 ) of the same triangle, they are equal if sequentially Area 1 = Area 2 , Length 11 = Length 12 , Length 21 = Length 22 , or reversely Area 1 = Area 2 , Length 11 = Length 22 , Length 12 = Length 21 .

(2)For two signatures Sig - _s1 { Sig - 11 , Sig - ₁₂,..., Sig - _1N } and Sig - _s2 { Sig - ₂₁ , Sig - ₂₂ ,., Sig - _2N }of the same set of N triangles, they are equal if sequentially Sig - 11 = Sig - ₂₁ , Sig - 12 = Sig - 22 , ., Sig - 1N = Sig - 2N , or reversely Sig - _n= Sig - 2n , Sig - 12 = Sig - 2 N-1 , ., Sig - 1N = Sig - 21 .

(3)For two signatures Sig _s1 { Sig - _x1 , Sig - _y1 } and Sig s2 { Sig - x2 , Sig - y2 } of a solution, they are equal if sequentially Sig - x1 = Sig - x2 , Sig - y1 = Sig - y2 , or reversely Sig - x1 = ^Sig - y2 , ^Sig - y1 = ^Sig - x2 .

The comparing criterion applies to the signature of permutation too. Under those definition, signatures of permutations on one orbit of N =9 shown in table 2 are all the same.

Table 2: signatures of permutation on one orbit of N =8

permutation (1, 6, 8, 3, 7, 4, 2, 5)

(1, 7, 4, 6, 8, 2, 5, 3)

(6, 4, 7, 1, 3, 5,

signature

{{(26, 3, 5), (5, 7, 26), (26, 9, 17), (17, 7, 10), (10, 1, 5), (5, 5, 10)},

{(37, 9, 10), (10, 5, 5), (5, 0, 5), (5, 8, 37), (37, 9, 10), (10, 5, 5)}}

{{(37, 9, 10), (10, 5, 5), (5, 0, 5), (5, 8, 37), (37, 9, 10), (10, 5, 5)},

{(26, 3, 5), (5, 7, 26), (26, 9, 17), (17, 7, 10), (10, 1, 5), (5, 5, 10)}}

{{(5, 5, 10), (10, 9, 37), (37, 8, 5), (5,

2, 8)

(8, 3, 1, 6, 2, 5, 7, 4)

(5, 2, 4, 7, 3, 8, 6, 1)

(8, 2, 5, 3, 1, 7, 4, 6)

(4, 7, 5, 2, 6, 1, 3, 8)

(3, 5, 2, 8, 6, 4, 7, 1)

0, 5), (5, 5, 10), (10, 9, 37)},

{(10, 5, 5), (5, 1, 10), (10, 7, 17), (17, 9, 26), (26, 7, 5), (5, 3, 26)}} {{(26, 3, 5), (5, 7, 26), (26, 9, 17), (17, 7, 10), (10, 1, 5), (5, 5, 10)},

{(5, 5, 10), (10, 9, 37), (37, 8, 5), (5, 0, 5), (5, 5, 10), (10, 9, 37)}}

{{(10, 5, 5), (5, 1, 10), (10, 7, 17), (17, 9, 26), (26, 7, 5), (5, 3, 26)},

{(37, 9, 10), (10, 5, 5), (5, 0, 5), (5, 8, 37), (37, 9, 10), (10, 5, 5)}}

{{(37, 9, 10), (10, 5, 5), (5, 0, 5), (5, 8, 37), (37, 9, 10), (10, 5, 5)},

{(10, 5, 5), (5, 1, 10), (10, 7, 17), (17, 9, 26), (26, 7, 5), (5, 3, 26)}} {{(10, 5, 5), (5, 1, 10), (10, 7, 17), (17, 9, 26), (26, 7, 5), (5, 3, 26)},

{(5, 5, 10), (10, 9, 37), (37, 8, 5), (5, 0, 5), (5, 5, 10), (10, 9, 37)}}

{{(5, 5, 10), (10, 9, 37), (37, 8, 5), (5, 0, 5), (5, 5, 10), (10, 9, 37)},

{(26, 3, 5), (5, 7, 26), (26, 9, 17), (17, 7, 10), (10, 1, 5), (5, 5, 10)}}

As can be seen, the signatures of all permutations on an orbit are all the same in the light of the definition of permutation signature and Sequential-Reverse criterion, so any one of them can be chosen to represent the signature of the orbit. Thus orbit signature is defined as the signature of any permutation on it. The global uniqueness of orbit signature is clear. If two orbits are from space of different order, whose numbers of LengthArea-triple are also different, so their signatures are definitely different. If two different orbits from the same space have the same signatures, this means their all Length-Area-triple are the same sequentially or reversely, that is to say, all adjacent triangles formed by every three adjacent queens are equivalent, so the layout of queens of these two permutations are totally the same, thus the two orbits must be the same. In a word, orbit signature gives a global unique identity to the orbit.

V Search algorithm based on Orbits

Based on orbit signature, an orbit-based search algorithm to solve N-Queens problem can be proposed as follows, and an example to demonstrate its effectiveness is given.

• A. Search algorithm

The idea is realized by a two-step search. The first step is to apply operator Inc to upgrade all orbits of order N . The second step is to apply operator Mov to current orbits in space of order N +1.

Orbit-based search algorithm procedure: search_orbits begin

//Step 1: use operator Inc to upgrade orbits from order N-1 to N for every solution on orbits in the space of order N-1

for every position (0.5, 1.5, ., N -0.5) x(0.5, 1.5, ., N -0.5)

• apply operator Inc to try to increase a queen; calculate orbit signature of the new solution;

• if the signature is unique, retain it and the orbit;

end for end for

//Step 2: use operator Mov to transmute current orbits repeat access orbits in the space of order N by breadth-first strategy or depth-first for every solution on orbits in the space of order N for every queen in the solution for every position (0.5, 1.5, .., N+0.5) x (0.5,

• 1.5, …, N +0.5)

• apply operator Mov to try to move a queen; calculate orbit signature of the new solution;

• if the signature is unique, retain it and the orbit;

end for end for end for until all orbits have been extended by the search strategy end

The positions of queens are given in the form of Descartes product. Advantages of the algorithm lie in that orbits can be obtained gradually from orbit space of order N -1 and N . Moreover, to obtain an orbit means to get at most eight solutions, which helps to promotes search efficiency for N-Queens problem.

• B. Case study

Taking N =8 for example, the following illustrates generation of all orbits based on solutions of N =7. During the search, a lexicographical generation algorithm for permutation in STL is used. Numbers of permutations are given by sequence of their generation, and numbers of 12 orbits are given by sequence of their generator.

(1)Use operator Inc to upgrade orbits from N =7 to N =8.

Orbit 1: Apply Inc (7.5, 0.5) to (2, 4, 1, 7, 5, 3, 6), and gets a generator (8, 2, 4, 1, 7, 5, 3, 6).

Orbit 2: Apply Inc (0.5, 7.5) to (2, 4, 1, 7, 5, 3, 6), and gets a generator (3, 5, 2, 8, 6, 4, 7, 1).

Orbit 9: Apply Inc (6.5, 0.5) to (2, 4, 1, 7, 5, 3, 6), and gets a generator (7, 2, 4, 1, 8, 5, 3, 6).

There are three orbits generated in the first step, which set up the basis of the second step.

(2)Use operator Mov to transmute orbits of N =8.

Orbit 6: Apply Mov (3, 1, 2.5, 8.5) to (3, 6, 4, 2, 8, 5, 7, 1), solution 22 on orbit 1, and gets a generator (6, 4, 2, 8, 5, 7, 1, 3), i.e. solution 77 on orbit 6.

Orbit 8: Apply Mov (4, 1, 3.5, 8.5) to (4, 2, 7, 3, 6, 8, 5, 1), solution 33 on orbit 1, and gets a generator (2, 7, 3, 6, 8, 5, 1, 4), i.e. solution 10 on orbit 8.

Orbit 7: Apply Mov (7, 1, 8.5, 3.5) to (7, 2, 6, 3, 1, 4, 8, 5), solution 83 on orbit 8, and gets a generator (2, 6, 8, 3, 1, 4, 7, 5), i.e. solution 9 on orbit 7.

Orbit 11: Apply Mov (5, 3, 2.5, 0.5) to (4, 8, 5, 3, 1, 7, 2, 6), solution 46 on orbit 7, and gets a generator (3, 5, 8, 4, 1, 7, 2, 6), i.e. solution 17 on orbit 11.

Orbit 3: Apply Mov (4, 6, 3.5, 1.5) to (4, 8, 5, 3, 1, 7, 2, 6), solution 9 on orbit 7, and gets a generator (3, 5, 8, 4, 1, 7, 2, 6), i.e. solution 5 on orbit 3.

Orbit 5: Apply Mov (8, 5, 2.5, 0.5) to (5, 7, 1, 3, 8, 6, 4, 2), solution 57 on orbit 3, and gets a generator (6, 8, 2, 4, 1, 7, 5, 3), i.e. solution 23 on orbit 5.

Orbit 4: Apply Mov (1, 2, 8.5, 1.5) to (6, 1, 5, 2, 8, 3, 7, 4), solution 65 on orbit 3, and gets a generator (5, 8, 4, 1, 7, 2, 6, 3), i.e. solution 64 on orbit 4.

Orbit 12: Apply Mov (7, 2, 1.5, 7.5) to (2, 7, 5, 8, 1, 4, 6, 3), solution 11 on orbit 9, and gets a generator (3, 6, 8, 1, 5, 7, 2, 4), i.e. solution 24 on orbit 12.

Orbit 10: Apply Mov (4, 5, 2.5, 0.5) to (5, 2, 8, 1, 4, 7, 3, 6), solution 53 on orbit 12, and gets a generator (3, 5, 2, 8, 1, 7, 4, 6), i.e. solution 14 on orbit 10.

Nine other orbits are generated gradually as above. The path to generate all 12 orbits of N =8 is shown in fig. 2. The trajectory of orbit generation forms a graph. However, generator of an orbit can be other solutions besides the one just used above, and sequence to generate all orbits varies in the light of different search strategies.

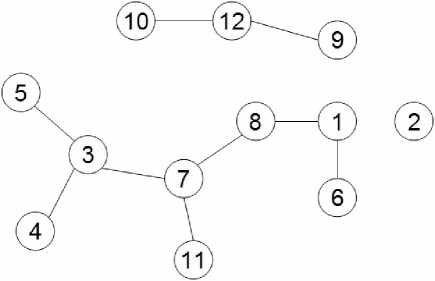
Fig. 2 One trajectory graph of orbit generation of N =8

№ Conclusion

In this paper, an algorithm to search solutions of N-Queens problem is proposed based on the orbit and group actions.

The main idea is composed of 3 steps. Step 1: to get a solution p by any algorithm [3]. Step 2: Apply permutation operation group on p to get the other solutions on the same orbit o . Step 3: Apply orbit operations on o to get the other orbits. Then all permutation elements on all orbits are all solutions of N-Queens problem.

To identify different orbits, this paper brings forward the concept of the orbit signature which gives every orbit a global unique identity. To operate on the orbit, this paper defines two operators, Inc and Mov, to upgrade and transmute the orbits respectively. To operate on elements on the orbit, this paper gives an isomorphism from D4 to permutation operation group PO. All the discussions utilize the theory of orbits, action of the group, and permutation.

There are two topics worth consideration in the future. The first one may focus on promotion of the computing efficiency and a faster implementation of the algorithm. The second one may focus on the optimal path to generate all orbits.

A CKNOWLEDGEMENTS

This work is supported by the National Key Basic Research Program of China under Grand 2005CB724103.