An Analysis of Fuzzy and Spatial Methods for Edge Detection

Published Online November 2016 in MECS DOI: 10.5815/ijieeb.2016.06.08

A method in which various input image properties is obtained as an output known as transition. Transition state of the input image to output image lay in the segmentation.

An Image segmentation splits an image into its subregions to collect the details which are found in a subregion of the image. These details are helpful to analyzing images for the enhancement of images. The accuracy of enhancement is based on accurate segmentation method. For this reason, more care should be taken to improve images with the help of accurate segmentation. It is helpful to control the environment in many applications like in military to detect objects, industrial inspection applications etc. An image segmentation method has two types of categories to achieve accuracy. The first category is describing a partition of images based on Sharpe changes in intensity known as edge and the second category is based on a set of predefined criteria known as Thresholding, region growing and region splitting and merging [1] [2]. With the help of thresholding edge, detection can be possible to overcome the criteria of the noisy condition. In this method first order derivative of Gaussian filter used for convolving the images [3]. Edges found by canny can also create some false edges. The structure of image can also find with the help of method known as USAN, which is helpful in edge detection [4]. Edges may also find with the help of zero crossing [5]. For measurement of the degree of fuzziness, entropy has used, which produced 1-pixel wide edges [6]. Image segmentation is a difficult task to make images meaningful. By using canny method image segmentation may give many false edges to increase the complexity of image characteristics. Instead of Canny method, a two steps Chan These method is helpful to detect best edges [7]. All the classical spatial methods like Canny edge detector, Sobel method, Prewitt edge detection, and Laplacian of Gaussian are not been able to detect correct and smooth edges in images. Latterly a new method intuitionistic fuzzy set (IFS) theory was proposed to detect correct and smooth edges. The intuitionistic fuzzy method used the concept of entropy in various clustering algorithm [9].

The remaining paper is divided as follows. Section II is describing various classical edge detection techniques available in the literature. Section III is describing fuzzy domain edge detection techniques. Section IV is based on experimental study and results. And in the last section V conclusions are drawn.

• II.    Spatial Domain Edge Detection Techniques

Spatial filtering is used in the Edge detection to used break off between gray levels. For the edge detection in images first order derivative and second order derivatives are used. First order derivative are worked out by using gradient and second order derivative are found by the Laplacian.

• A.    Gradient operator

The gradient of an image /( x, y) at a location ( x, y) is defined as the vector:

^=н=ш       (1)

Magnitude of above vector:

Vf = mадф f) = ^+^     (2)

The direction of the gradient vector:

a (x,y) = tan ^l(^)              (3)

Different types of edge detection methods are based on three categorizations:

• B.    Classical edge detection methods:

• i.    Sobel Mask

Mask used by this method is:

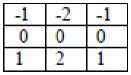
Fig.1. Sobel Mask

-1	0	1
-2	0	2
-1	0	1

Using the below equations Sobel mask is used for edge detection.

Gy = ^(Z 7 + 2 ^Z8 + ^Z9 ) - ^(Zl + ^2Z 2 + ^Z3 )      ⁽⁴⁾

Gy = (Z 3 + 2Z₆ + Z 9 ) — (Z i + 2Z ₄ + Z 7 )     (5)

• ii.    Prewitt Mask

Mask used by this method is:

-1	-1	-1		-1	0	1
0	0	0		-1	0	1
1	1	1		-1	0	1

Fig.2. Prewitt Mask

Using the below equations Prewitt mask is used for edge detection.

Gy = ^(Z7 ^{+ Z} 8 + ^Z 9 )   ^(Z l ^{+ Z} 2 + ^Z3 )       ⁽⁶⁾

Gy = ^(Z3 + ^Z 6 + ^Z 9^ - ^(Zl ^{+ Z}4 ^{+ Z}7 )       ⁽⁷⁾

• iii.    Robert Mask

Mask used by this method is:

-1	0
0	1

-1	0
о	1

Fig.3. Robert mask

Using the below equations Robert mask is used for edge detection.

G_x = (Z 9 — Z₅ )                (8)

Gy = ( Z 8 — Z 6 )               (9)

• C.    First order edge detection method

• i.    Canny edge detection

• •    It uses smoothing as a process to remove noise.

• •    Finding the gradient of images which has a large magnitude.

• •    By using double thresholding.

• D.    Second, order edge detection method

• i.   Laplacian

The Laplacian of a 2-D function f(x,y) is a second-order derivative. The Laplacian is merged with smoothing to find edges via zero-crossing.

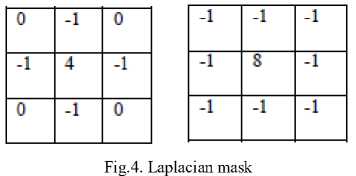
In Laplacian filtering enhanced image can be found by:

F' (x.y) = F(x, y) + CVF(x, y)         (10)

• ii.    Laplacian of a Gaussian (LOG)

Laplacian of a Gaussian sometimes is called the Mexican hat function. Gaussian function is used to smooth the image and Laplacian operator is used to constitute the location of edges by zero findings. Here, Figure-5 is a 5×5 mask to approximate the shape of Maxican hat function.

0	0	-1	0	0
0	-1	-2	-1	0
-1	-2	16	-2	-1
0	-1	-2	-1	0
0	0	-1	0	0

Fig.5. Laplacian of Gaussian Filter

• III.    Fuzzy Domain Edge Detection Techniques

In many applications, edge detection becomes very important due to the criticality of use of images like in medical images diagnosis of disease is very crucial. Due to this reason, images must be free of poor contrast, vagueness, blurred or broken edges. That’s why because of the above reasons fuzzy method is suitable to take into account the unclearness and equivocalness present in the image [17]. Several Fuzzy edge detection methods are following:

• A.    Fuzzy Sobel edge detector [13]

In this method the image is divided into two regions:

• i.    Fuzzy edge region

In this method, if pixels have a high difference in the gray level with their neighborhood region then the pixels are separated by the fuzzy edge region.

• ii.    Fuzzy smooth region

In this method, if pixels have less difference of gray level with their neighborhood region then the pixels are separated by the fuzzy smooth region.

By using fuzzy reasoning the modified fuzzy edge detector is generalized by using following fuzzy rules:

R(x, y) = 255, if G(x, y) ≥ HT           (11)

= 0, if G(x, y) ≤ LT

= G(x, y).max (     (x, y),     (x, y))

Otherwise

Where     and     are the membership functions of the image smooth and edge regions.

G(x, y) is the gradient value using Sobel operator.

R(x, y) is the resultant pixel at location(x, y).

• B.    Entropy-Based Fuzzy Edge Detection [11]

As per information theory, defined formula of entropy is given as:

H (t1, t2) = -              () –

(      )(12)

Whereare

Probability distributions.

= ∑ ℎ .     (k)(13)

Psm о о t h = ^khgk-Ssmo о th(k)

Here          and       are weight area on the gradient histogram and when membership function and      are weights.

In edge detection, the best parameter values are compact edge representation of images that’s why minimum entropy H (   _,  ) parameters are selected.

The necessary assumptions for minimum and maximum entropy are:

∂H ( ,  ) /∂  = 0 = - (∂        / ∂ Χ log (/

1-))

∂H ( ,  ) / ∂  = 0 = - (∂        / ∂ Χ log (

/ 1-))

The entropy will be minimum,

When       =     = ½(17)

The best set of parameter ( ^̃ , ^̃ ) will satisfy the following condition:

H ( ̃ , ̃ ) = min , , … (  (  (r),   (r)))(18)

The edge image is calculated as

Edge – image(x, y) = 1(19)

• C.    Fuzzy template based edge detector

Two types of fuzzy template based edge detector method are available.

In first method, fuzzy edge templates are designed and these templates are convolved with the image [12].

For finding the existence of edge:

H(x, y) = max ,    (   ( , ))        (20)

Where n=number of templates.

The new images are found with the support of threshold, the value which is below the threshold are set as 0 and above the threshold are set as 1.

In second method fuzzy divergence used in between image window and a set of 16 fuzzy templates [8].

• D.    Fuzzy If-then Rules based Edge Detection

This fuzzy technique is based on rule-based fuzzy logic. The fuzzy rule-based concept has been taken from Fuzzy set theory [14] [15] because of its simplicity and effectiveness. It is an inference form of uncertain knowledge to handle and analyze information in an effective manner. It could be combined different filters along with fuzzy if-then rules to detect edges for enhancement of images [16]. For edge detection fuzzy logic algorithm using following rules [1]:

• (1)    If a pixel belongs to the same region, then make it brighter; else make it darker, where values related to brighter and darker are fuzzy sets.

• (2)    A 3x3 pixel neighborhood and corresponding intensity differences between the center pixels and its neighbors are shown below.

  21	23	2a
  Z4	Z?
  2-	Ze	z9

  
  

  	d2	da
  ^5	0
  d,7

  
  

Fig.6. 3x3 mask

The followings are the if-then-else rules based on fuzzy values.

IF

IF

IF

IF

ℎ ℎ

ℎ

ℎ

ELSE z5 is black

Membership functions ZE, BL, and WH is used for the fuzzy sets zero, black, and white.

• IV.    Experimental Study and Results

In this study, several images have taken from internet and Matlab for the experiment of edge detection. Followings are the procedure of edge detection using fuzzy If-then rules:

Step-1: Apply the simple filters (convolution) to obtain the image gradients.

Step-2: Define the image gradients of input image with respect to x-axis and y-axis direction.

Step-3: Design a Fuzzy Inference System (FIS) with 2 inputs and 1 output.

Step-4: Set the Fuzzy-If Then Rules into FIS.

Step-5: Obtain the membership function of image gradients as Ix and Iy.

Step-6: Apply the Ix and Iy to above FIS for Evaluation. Step-7: Store the result obtained from output of FIS. This resultant would produce the edge of the image.

In this, we are comparing various classical method of edge detection with fuzzy if-then-else rule-based edge detection method. Based on performance evaluation parameters, we can compare various methods.

In the experiments, we have compared various methods of edge detection on the basis of two performance analysis parameters. One is PSNR and another is MSE, below every output image these values are written and we can compare on the basis of these values, which method is giving better results.

The mathematical formula of the PSNR is as follows:

PSNR = 20 Log₁₀ (    )           (21)

Where, MSE (Mean square error) is as follows:

MSE =     ^∑ о" ^{1 ∑}О ¹  ⃒⃒f( i,j) – g(I, j) ⃒⃒  (22)

Where f = matrix data of the original image, g = matrix data of the degraded image, m = no of rows of pixels of an image, I = index of that row, n = no of columns of pixels of an image, j = index of that column.

Higher the values of PSNR will show better results because only on the basis of visualization strongly we cannot reach the conclusion, which method is better.

Table 1. MSE values of different images

	Image 1	Image 2	Image 3	Image 4
SOBEL	12698.83	14161.36	17974.31	17702.02
PREWITT	12698.91	14161.36	17974.38	17702.12
ROBERT	12699.58	14163.92	17974.16	17702.16
CANNY	12683.91	14161.25	17962.88	17693.80
FUZZY IF-THEN ELSE	0.34	0.34	0.24	0.27

■ Image 1

■ Image 2

■ Image 3

■ Image 4

Edge detection methods

INPUT

IMAGES

Fig.7. PSNR values of different images

(a) Kid image

(b) Rice image

(c) Cameraman image

(d) Lena image

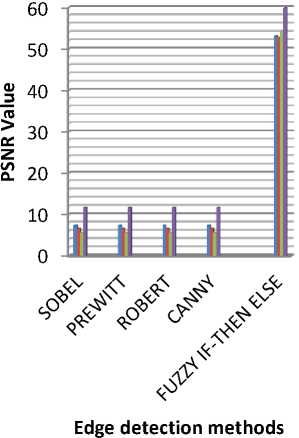
Fig.8. Results of various edge detection methods table 2. psnr values of different images.

	Image 1	Image 2	Image 3	Image 4
SOBEL	7.40	6.65	5.62	11.71
PREWITT	7.40	6.65	5.62	11.71
ROBERT	7.40	6.65	5.62	11.71
CANNY	7.40	6.65	5.62	11.71
FUZZY   IF- THEN ELSE	53.14	52.79	54.34	59.87

• ■    Image 1

• ■    Image 2

• ■    Image 3

• ■    Image 4

Fig.9. PSNR values of different images

• V. Conclusion

In this paper, edge detection based on image segmentation of various spatial methods and fuzzy methods are discussed and compared the result of various spatial edge detection technique and fuzzy if-then method. The experimental study is performed on various images collected from internet and Matlab. As per experimental results fuzzy method is giving better results as compared to spatial fuzzy methods like Sobel, Prewitt, Robert and Canny on the basis of visualization and with the help of quantitative values of performance parameters like PSNR, and MSE. The values of PSNR of the fuzzy method are higher as compared to other methods. Graphs of MSE values and PSNR values clearly showing better result of fuzzy if-then else method on the basis of their higher values of PSNR. However, fuzzy edge detection method is giving better results.