An analytical study of cellular automata and its applications in cryptography

Published Online December 2017 in MECS

• I.    Introduction

  Cellular automata were invented in the early 1950's by J. Von Neumann [1]. Afterwards, Stephen Wolfram developed the cellular automata theory [2]. It is now becoming an attractive for researchers of various fields due to its parallel structure in nature. It is used in engineering and science field. The reason behind the popularity of cellular automata can be traced from their simplicity and the enormous potential that they hold for designing complex systems [3].

With the rapid growth of distributed applications, services and shared resources through the internet, the need for user security [58, 59] becomes more important in order to ensure security and effective access control. Cryptography methods in many applications are considered as a real time process in which the process speed and optimization solution are essential. Therefore, the parallel algorithms in cryptography methods are much more important than sequential algorithms. Many researchers widely used [14, 27, 31, 43] cellular automata concept in cryptography because of its parallel structure and ability to design complex dynamic systems in nature.

Cellular automata is a collection of cells arranged in dimensional lattice, for each cell state change as a function of time, according to a defined set of protocols that include the states of the neighboring state cells. Typically, the rule for updating cells state is the same for each cell, it does not change over time and it is applied to the whole grid simultaneously. Hence, the new state of each cell, at the next time step, depends only on the current state of the cell and states of the cells in its neighborhood. All cells on the lattice are updated synchronously. Thus, the state of the entire lattice advances in discrete time steps. It is clear that the concept of inherent parallelism is implicit to cellular automata [4, 5]. Most authors used [18, 46, 48] two types of cellular automata, such as one dimensional cellular automata and two dimensional cellular automata [57]. If the grid cell is linear array it is called one dimensional cellular automata and if the grid cell is rectangular or hexagonal it is called two dimensional cellular automata. Cellular automata having one central cell and four near neighboring cells is called a Von Neumann five neighborhood cellular automata. Whereas, cellular automata having one central cell and eight near neighboring cells is called Moore eight near neighborhood cellular automata [6].

Many researchers proposed cellular automata for public key cryptography [25, 27, 29, 31] because it is very difficult to reverse the transition rule until the corresponding transition rule is known. Due to this advantage, most researchers proposed cellular automata transition rule as a key in the cryptography methods. According to the Kerckhoff's principle [7], only secrecy of the key provides security . After that, Shannon was reformulated as the enemy knows the system [8]. So, the key should be kept secret in any security designs. Hence, a cellular automata is the perfect method to implement the secret keys.

The rest of the paper is organized as follows: Section II introduces the methods of cellular automata. In section III, we discuss a study of different types of cellular automata over the last decades. In section IV, a wide range of applications in cellular automata proposed by many researchers are presented. In section V, we present a comparative study on the existing cellular automata based cryptography. In section VI, we conclude the study paper.

• II.    Overview of Cellular Automata

Cellular automata is a collection of cells arranged in regular grid [9] of lattice, when each cell has its own state changing in a discrete time stamp. Each state of the cellular automata cells will be updated simultaneously using a local transition rule, which defines every new cell state uses previous cell state of the corresponding neighbors. The specific selections of neighbor cells are relatively chosen with the given cell position that can be defined for every cell using a radius r on the particular lattice. This gives 2r + 1 different neighbor, including the current cell.

• A.    Rule of One-Dimensional Cellular Automata

Elementary cellular automata have two possible label values for every cell, i.e., either it will be 0 or 1. The rule depends only on the nearest neighbor label values. As a result, the evolution of elementary cellular automata can be completely described by the next generation, based on the label value of the cell to its left, the label value of the cell itself and the label value of the cell to its right. Hence, there are 2 x 2 x 2 = 23 = 8 possible binary states for the 3 cells neighboring to a given cell, so, there are 28 = 256 elementary cellular automata rules are possible for every cell that can be indexed with an 8 bit binary number.

According to the wolfram’s, a new kind of science [3], Fig. 1 shows that the evolution of rule 30 (30 = 00011110 2 ) with n generations of elementary cellular automata rule r implemented as [ r , 1,0, n ] .

• B.    Rule of Two-Dimensional Cellular Automata

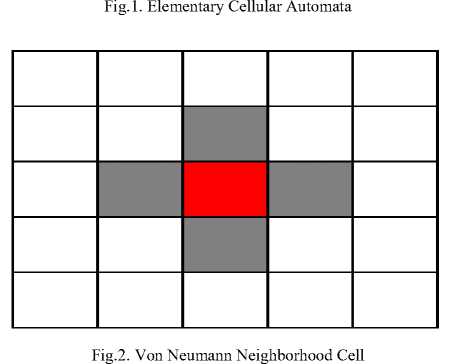
Two-dimensional cellular automata display some of the same characteristics as that of one-dimensional cellular automata. There are two types of neighborhood states are mainly considered. First one is the Von Neumann neighborhood [10] states as shown in Fig. 2. It consists of four or five cell array which depends on whether the center cell is counted or not.

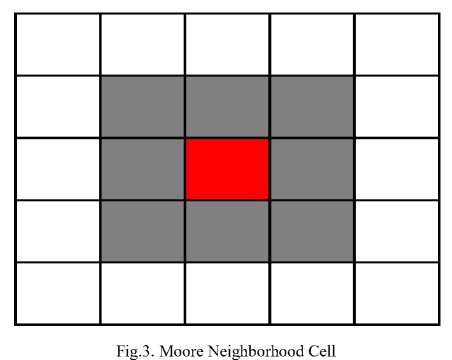
Second one is the Moore neighborhood [11] states as shown in Fig. 3. It consists of eight or nine cell array which depends on whether the center cell is counted or not. In both cases r = 1 and each one is helpful based on the context. The extended Moore neighborhood has the same characteristics but with . In one-dimensional case with ( k , r ) = ( 2,1 ) there are possible neighborhood states configuration are available which have binary states either 0 or 1. In nine cell Moore neighborhood case, there are possible neighborhood states configuration are available. Hence, there are possible transition rule functions to choose from this Moore nine cell neighborhood cases. Even with a five cell neighborhood case, there are still billion possible transition rule functions available to choose from this Neumann five cell neighborhood cases. Hence, two-dimensional cellular automata are mostly used for random number generation in cryptography method.

• III.    Different Types of Cellular Automata

Today, many researchers are proposing different types of cellular automata models and designs in a complex system. Hence, this section highlights various types of cellular automata.

• A.    Reversible Cellular Automata

Faraoun Kamel Mohamed discussed [12] a parallel block based encryption scheme for digital images using reversible cellular automata. According to his information, cellular automata is said to be reversible, if its global map is self-invertible. It means each possible state have only one successor and it achieves inherent parallel mechanisms, un-decidability of testing reversibility and dynamic states in nature. Due to this advantage, many researchers used this mechanism in cryptography.

• B.    Fuzzy Cellular Automata

Maji et al. discussed the idea of using fuzzy cellular automata [13] for modeling pattern classifiers. Here, cellular automata employed with fuzzy logic. An interesting class of cellular automata referred as fuzzy cellular automata [14] is employed to design the pattern classifier from theory to applications. Hence, all states cell and local transition rules are having fuzzy logic in cellular automata.

• C.    Additive Cellular Automata

Nandi et al. presented [15] a theory and applications of cellular automata in cryptography. They discussed a new method of cellular automata and its method having a combination of XOR (Exclusive-OR) and XNOR (Exclusive-NOR) transition rules. Hence, this technique is said to be an additive cellular automata which may be used in block cipher encryption technique in cryptography.

• D.    Uniform Cellular Automata

Uniform cellular automata had been discussed by Nandi et al. [15]. If all the cells have the same type of transition rules in cellular automata, then it is said to be a uniform cellular automata or regular cellular automata.

• E.    Linear Cellular Automata

Nandi et al. discussed [15] the concept of linear cellular automata. Cellular automata whose local transition rule function involves the algebraic function XOR in any of the cell, is called as linear cellular automata.

• F.    Non-Linear Cellular Automata

The characteristics of non-linear cellular automata were presented [16] by Jun-Cheol et al. Cellular automata whose local transition rule function involves boolean values in any of the cell is called as non-linear cellular automata.

• G.    Generalized Multiple Attractor Cellular Automata

Ponkaew et al. discussed [17] a non-linear classifier generalized multiple attractor cellular automata (GMACA) using an evolution of cellular automata. It is the special class of cellular automata, especially used in genetic algorithm for efficient implementation. Most of the GMACA designed for complex system because, it reduces the space and time. Due to this advantage, many researchers preferred to choose this special class of nonlinear cellular automata.

• H.    Hybrid Cellular Automata

Anghelescu et al. discussed [18] an idea of implementing hybrid cellular automata encryption algorithm. Cellular automata whose local transition rule function is different for all the cells, is called as hybrid cellular automata.

• I.    Programmable Cellular Automata

Encryption algorithm using programmable cellular automata was proposed by Anghelescu et al. [19].

A programmable cellular automaton applies some values of control signals on a cellular automaton structure. During the run time, it specifies the values of control signal and it can be implemented by using various local transition rule functions in cellular automata.

• J.    Null boundary Cellular Automata

Null boundary cellular automata had been analyzed by Kundu et al. [20]. Null boundary cellular automata is one in which the maximum cells are connected through logic-0 states which is called as null boundary cellular automata.

• K.    Complement Cellular Automata

Nandi et al. discussed [15] a concept of complement cellular automata. Cellular automata whose local transition rule function involves XNOR logic operation in any of the cell, is called as complement cellular automata.

• L.    Periodic boundary Cellular Automata

Anghelescu et al. proposed [18] a model of periodic cellular automata. Periodic boundary cellular automata is one in which the maximum cells are connected through each other cell which is called as periodic boundary cellular automata.

• IV.    Applications of Cellular Automata based Cryptography

Since the beginning of cellular automata in the cryptography field, it has been found that, it is used to classical encryption and decryption schemes, either as their main support or one of the components support. Hence, this section highlights the various applications of cellular automata based cryptography.

• A. Secret Key Sharing Scheme

  Generally, in a secret key sharing scheme, secret information will be shared between different parties and then, a selected subset of those parties can recover the secret information. Application of automata in secret sharing scheme includes the threshold cryptography scheme [21] and attribute based encryption scheme [22]. In threshold scheme ( x,h ) we construct the secret information within the quantitative limit. For example, if x or more parties combined their pieces, then each piece is distributed among h parties. Hence, the only way to reconstruct the secret information is threshold scheme. In 1979, Shamir [23] and Blakley [24] simultaneously introduced a series of ( x,h ) threshold schemes in cryptography. All previous works handle this problem in a similar way.

In 2003, Maranon et al. [25]. introduced the application of automata in secret information sharing schemes. The authors proposed ( x,h ) threshold scheme based on two-dimensional linear memory cellular automata with Moore neighborhood having radius size 1 and an alphabet q . Especially, they targeted image size of p × q bits as the secret, therefore the number of cells of the cellular automata is p × q . Hence, in order to consider Moore neighborhood with two-dimensional cellular automata, the state of the cell ( m,n ) can be given by:

Т¹ +1 ( m , n ) =   £    ц₅ , p ^Т x

• 5 , p e ( -1,0,1 )

( m + 5 , n + p )( mod v )              (1)

where ψ represents the global state or global configurations, ψ +1 be the global state of the cells at time t +1 with 0 < m < p-1, 0 < n < q-1,  % p e Z2 and v = 2y represents the number of colors of the image, because each cell has now 9 neighboring cells, so there are 29 = 512 possible two-dimensional linear cellular automata available in this configuration. Each one is specified by the rule number Ω which is given by:

Q = 7 7 - 1, - 1 2 ^{+ п} - 1,0^{2 +} 7 7 - 1,1 2 ⁺ 7 7 0, - 1 2 +

Пи, 24 + По1 23 + П1,-122 + П1,о 21 + Пц20

with 0 ≤ Ω ≤ 511 possible configuration available. Let ^U‘mn ^ ( Z 2 ) 9 represent the state of the neighboring cells of cell m . Now, it becomes:

• X - 1             s,

Т ‘+1 ( m, n )=  £ fe+1 (Umne )(mod v)

e = 0

with 0 <  m <  p - 1,0 <  n <  q - 1 and 1 <  n <  x , it denotes the local update function of some x two-dimensional linear cellular automata. Eq. (3) is reversible, if the following condition holds:

f x ( U™ ⁺¹ ) = Т t ^{- x +1} ( m , n )             (4)

This is another inverse of linear memory cellular automata with local transition function given by:

x — 2

Т t ^{+ 1} ( m , n ) = - £ f x - e-S U m-n ) + e = 0

Т t ^{- x + 1}( m , n )(mod v )             (5)

with 0 <  m <  p - 1,0 <  n <  q - 1. Eq. (3) and Eq. (5) have  the  same size  as the original and  also

V0 (v), v (v) ,^2 (v),......,^x-1 (v) are populated with data from the  image  and random matrices.  The configuration v0 (v) is populated with the secret image, while other x-1 configurations are randomly generated in a sequence. So, each participant or group receives one subsequent cellular automata configuration, it is randomly selected.

For example, if there are h participants involve, then each participant will receive one of the h final configurations of the cellular automata. According to the authors, if any one of the x configurations is missing, we would need to solve an under determined system in order to recover the secret image in the available configurations. Even though the good security results from the above scheme, Jafarpour et al. [26] proved that they are vulnerable against fraudulent participant’s collision by cheating. To reduce the vulnerability, many researchers presented with different authentication methods. In 2010, Eslami et al. [27, 28] presented a new authentication method in cellular automata. In 2013, Sujata et al. [29] proposed an enhanced authentication method based on cellular automata. After that, multiple secret sharing schemes have been proposed [30, 31] in many cases. However, with a large number of technically advanced attackers out, there is a skill to launch a successful attack against any security system.

• B.    Hash functions with Cellular Automata

In modern cryptography, cryptographic hash functions play a vital role in real time environment [32]. Now-a-days, different type of hash functions are applied to a real time environment, which includes timestamps, message authentication, digital signatures and one time passwords [56]. A hash function maps an input message m of an arbitrary length to different or same length output, called a message digest. Hence, if the message was modified or altered, the message digest is no longer valid for any reason. In such situations the data may be corrupted, which is considered as the one type of efficient mechanism to identify the data corruption.

One way hash function maps an input message m of an arbitrary length to a fixed length of an output hash value which holds the following properties:

• •    Given the hash value h , it is very difficult to invert the message m , called pre-image resistant one way hash function.

• •    It is totally infeasible to find two messages m and m' , such as h ( m ) = h ( m' ), called second pre-image resistant hash function.

• •    Hash function mathematically infeasible to compute another message m' such as h ( m ) = h ( m' ), if the message m is given, called collision resistant hash function.

In 1989, the first attempt was made by Damgard [33] to build a fast and collision free one way hash functions using cellular automata. After that, many researchers studied cellular automata based one way hash functions. However, they provided neither any specific neighborhood state nor any valid rule, but still the validity of their system is unknown. Hence, without cellular automata rules, it is not possible to determine the characteristics of the entire scheme and also they didn't provide enough experimental results on the security of their scheme. The only belief is that, the security of the system is based on diffusion and confusion. In 2013, Jeon et al. [34] proposed architecture of parallelism and logical bitwise operations based on cellular automata, the author’s entire system structure is somewhat looks simple but it lacks an in-depth security analysis. In 2015, Belfedhal et al. introduced a fast and efficient design of a programmable cellular automata based hash function [35]. Their system prevents statistical attacks and provides high sensitivity to input changes. However, it is not best suitable for the efficient software implementation in real time environment and the security analysis of their scheme is not up to the mark.

• C.    Substitution Boxes with Cellular Automata

A Substitution Box (S-Box) is one of the primary areas of symmetric key cryptosystems; this same key cryptosystems include Advanced Encryption Standard (AES) [36], Data Encryption Standard (DES) [37] and Blowfish [38]. Basically, S-Box takes m input bits that transform to n output bits. Cellular automata have the same ability as turing machines, which are simulated in any boolean functions with cellular automata.

In 2008, Szaban et al. proposed a model of 8 × 8 S-Box by using cellular automata [39], which is similar to the S-Boxes used in AES scheme. According to the authors, the test results showed that, for every 8-bit cellular automata rule numbers, such as 30,57,86,99,135 and 149, holds the similar results as that of traditional design S-Boxes. It verified that, cellular automata rule numbers 57 and 99 were not suitable for their scheme, due to the increased size of the cellular automata. Only 21 (out of 256) possible outputs were generated by the S-Boxes.

Due to this disadvantage, Szaban et al. [40] introduced the construction of 6 × 4 S-Boxes by using cellular automata, which is similar to the S-Boxes used in DES scheme. The authors reused the same rules as used in previous work [39]. The testing results showed that, in many cases, the low autocorrelation and non-linearity were better than traditional tables of DES substitution boxes. The authors also mention that cellular automata based S-Boxes hold three main advantages in opposition to traditional S-Boxes, such as,

• •    Dynamic in nature, i.e., if you are changing the rules; the entire S-Box table will be changed.

• •    Due to the inherent parallel nature of cellular automata, their memory footprint can be reduced.

• •    When compared to the classical schemes, cellular automata implementation is very fast and accurate.

After that, many researchers proposed [41,42] different S-Box techniques based on cellular automata, but their schemes lack efficient implementation and provide an optimal solution to the classical S-Boxes. Due to these disadvantages, in 2016, Gangadari et al. [43] proposed a novel approach for reversible cellular automata based substitution boxes. When compared to the existing works, their scheme provides better security and implementation. However, their in-depth security analysis is not enough for the current situation.

• D.   Block Encryption with Second order Cellular

Automata

In view of the two state boolean values, the second order cellular automata where the state of an each cell at instant time t + 1 depends on the neighborhood state configuration time at t and the state of cell instant at with the state [44] such that:

Tt+1 (k) = f (Tt (k - n),..., Tt (k),..., Tt (k + n),Tt-1( k - n),..., Tt-1( k),..., Tt-1( k + n ))     (6)

where ψt(k) is the state of cell k at instant time t, f is the local transition function and n is the neighborhood radius values. Hence, due to these additional dependency and associating two elementary cellular automata, we can make the reverse rules R1 and R2. The two elementary cellular automata rules must be related to each other with the following condition:

R = 2

dD

R = 2 d - R - 1              (7)

where dimension d = 2^{2 n +1}, the rule R defined by the following equations:

According to the Eq. (8), by increasing the size of dimension (D) from 1 to 2, it will be increasing the number of possible rules from 256 to 2⁵¹², that is nearly 1.341 X 10¹⁵⁴ rules. First, define the state transition rule; the cell at current t - 1is in state '1'. Second, define the state transition rule; the cell is in the state `0'.

RULE 30

**^4 H ?^ тч 4^11 ^^ ih^

Fig.4. Second Order Cellular Automata Rule

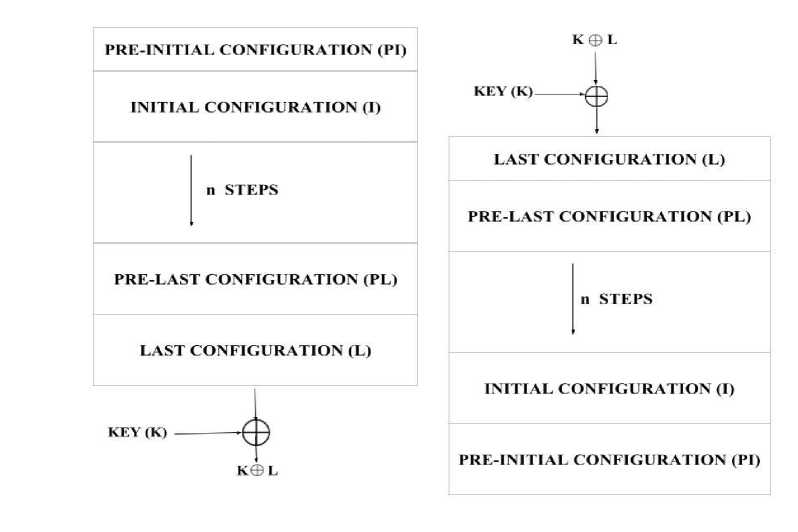
Fig.5. Process of Encryption and Decryption

Fig. 4 shows that, how these second order cellular automata rule can be represented in nature. For example, by selecting rule R 1 = 30 and n =1, from Eq. (7), we can make the number of second order rules with the following condition:

R₂ = 2 8 - 30 - 1 = 225 (9)

Now, we start with how these second order cellular automata are applied to cryptography methods. After arranging the pre-initial and initial configuration (Plaintext), the encryption process has been done by the pre-defined number of n steps, as shown in Fig. 5. After completion of encryption (pre-last configuration considered as a Cipher text), the last configuration XOR with the private key. Therefore, each and every step needs the two previous configurations, pre-last and last configurations should be saved in the system, because they required for the decryption process. Then, the cellular automata should be repeated for the same number of steps, as in the encryption process and the resulting configuration (Plaintext) will be next to the pre-initial configuration. Hence, considering this single second order reversible rule and its few iteration steps is not safe in the encryption and decryption process. Due to this disadvantage, Seredynski et al. proposed [45] a new cryptosystem, in their system provides more security and -used multiple rounds of data transformations and manipulations. However, their system faces brute force attack based on the block key size. To prevent any possibility of attacks, the block size should be enhanced from 64 bits to 128 bits. After that, Chai et al. increased [46] the block key space in an effective way, but still their system is not suitable for software implementation. Then, Zhang et al. presented with a new T-shaped neighborhood structure [47] and generated some second order reversible rules. Hence, the result shows        that, their system prevents from statistical and linear attacks. However, their system needs more in-depth security analysis.

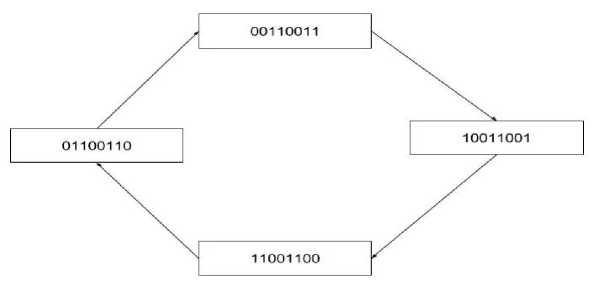
Fig.6. Unity Attractor Rule 85

• E.    Attractors with Elementary Cellular Automata

  In 2013, Abdo et al. introduced [48] a new cryptosystem, based on the cyclic behavior of some elementary cellular automata. After k steps, it enters into the cryptosystem. Cellular automata involves in a cyclic path, it is called an attractor. All other paths that are not part of the cycle are called transients and they open in inaccessible state and in states that cannot be reached from another state. Therefore, all the paths and transients may lead to form a basin cyclic form of some elementary cellular automata and the cyclic path properties form a basis of the cryptographic scheme. By performing an XOR operation, the encryption has been done between plaintext and t configurations of a cyclic path, with the interval between . To decrypt the encrypted text, we require XOR operation cipher text with the remaining configurations of the unity attractor. If G is considered as a plaintext and B is considered as a cipher text, the decryption XOR operation is performed with the following equations:

B = G ф ( ф t.^Ci )

G = B ф ( ф n_{=t +} Ci )            (11)

The cipher text ( B ) with where, cⁱ represents the configuration of the cellular automata at instant i . For example, by applying (plaintext G = 10101100 with t = 2) in this input to unity attractor rule 85, as shown in Fig. 6.

From Eq. (10), we calculate the cipher text:

B = 10101100 ф (11001100 ф 10011001) = 11111001                  (12)

We know that from Eq. (11), we can retrieve the plaintext:

G = 11111001 Ф (01100110 ф 00110011) =

10101100                 (13)

Hence, this cryptosystem consist of three parameters such as number of steps ( k ), an attractor with rule to apply and these control parameters that are generated with the help of plaintext. So, different plaintext generates different control parameters in an effective way. Hence, the result shows that this cryptosystem is used to prevent known and chosen plaintext attack. However, their cryptosystem key space is not enough in the current situation. Later, in 2017, Niyat et al. presented [49] a color image encryption scheme based on cellular automata. In their system holds the large key space and also resists the noise attacks. However, their system indepth security analysis is not up to the mark in the present situation.

• F.    Random Number Generators with 2-Dimensional Cellular Automata

The random number generator plays a major role in cryptography methods. It is used to generate cryptographic keys and some other vital parts of cryptographic protocols  and  algorithms  such  as initialization vector. It is a deterministic algorithm which generates random number in a uniform way. In 1997, Knuth [50] studied an excellent overview of pseudo random number generation (PRNG), whose information is a good cryptographic pseudo random number generation that produces a sequence of repeatable, but high quality random numbers. However, many researchers generally ignored this information. In the end, they generate an insecure generator. If they are used in cryptography schemes, it is relatively easier to guess the encryption keys. Poorly designed pseudo random number generators can easily damage an excellent cryptographic system. Later, Rock et al. [51] introduced a most popular technique to generate a pseudo random number such as linear feedback shift registers and linear congruential generators. However, these generators are not sufficiently good for cryptographic applications in real-time.

In 1980, Wolfram’s started a method of using application of cellular automata in cryptographic pseudo random number generators. He proposed [52] a new cryptosystem using a pseudo random number generator (Rule 30) based on one-dimensional cellular automata with periodic boundaries [53]. At the time of the research period, he described that the minimum number of evaluations required for the automata to repeat a configuration depends on initial seed and the size of the cellular space. After his evaluation, he noted that the statistical properties of the random stream are better if its size is much shorter than the period of the generator in the sequence. Meier et al. [54] had been broken by the wolfram’s cryptosystem with chosen plaintext attack, where they indicated that the sequence of configurations of the system is not hard to recover. Before the attack was identified, wolfram also challenged [53] that the problem of recovering the seed of its pseudo random number generator was NP-complete problem.

Since the attack was identified, the new type of hybrid or non-uniform cellular automata [15] was introduced and used multiple rules instead of using single cellular automata rules. They proposed a stream and block cipher, but focused on only non-uniform cellular automata with null boundaries. However, Blackburn et al. [55] had been broken by this block cipher scheme. After that, many researchers presented [19,41] different type of techniques and methods based on cellular automata. However, it is a significant challenge to generate a sequence of repeatable and high quality random numbers in an efficient way.

• V.    Comparative Study On Existing Cellular Automata Based Cryptography

Table1. shows the general issues in cryptography methods and solutions given by the cellular automata applications.

Table 1. Existing Cellular Automata based Cryptography

S.No.	Author Name	Issue	Cellular automata solution
[25]	Maranon et al.	Image security	Two-dimensional cellular automata
[31]	Li et al.	Data security	Linear memory cellular automata
[33]	Damgard et al.	One way hash functions	One-dimensional cellular automata
[35]	Belfedhal et al.	Authentication	Programmable cellular automata
[39]	Szaban et al.	Data security	One-dimensional cellular automata
[43]	Gangadari et al.	Data security	Second order reversible cellular automata
[45]	Seredynski et al.	Reduce the synchronization	Uniform and reversible cellular automata
[47]	Zhang et al.	Data security	Second order reversible cellular automata
[48]	Abdo et al.	Image security	Elementary cellular automata
[49]	Niyat et al.	Image security	Non-uniform cellular automata

• VI.    Conclusions

In this work, we gave a general introduction to cellular automata and its applications in cryptography. We discussed and presented, cellular automata is an efficient, fast and flexible tool for cryptographic methods. We have also studied and compared various types of cellular automata applications in cryptography.

Acknowledgment

This work was supported by the University Grants Commission in India under Rajiv Gandhi National Fellowship (Award Letter Number: F1-17.1/2015-16/RGNF-2015-17-SC-TAM-4667).