An approach to determination of maximal cliques in undirected graphs

Published Online January 2018 in MECS DOI: 10.5815/ijmecs.2018.01.01

The Maximum Clique Problem (MCP) is one of the well-known NP-hard problems in the graph theory. There are not algorithms for solving it in polynomial time. Nevertheless, the problem has numerous applications. In bioinformatics MCP is applied in the computer analysis of genomic databases (e.g., search for potential regulatory structures of ribonucleic acids). In social networks MCP is used in database clustering to divide various communities into groups (clusters) of common properties. Clusterization allows processing each of them by a secondary server. In chemistry MCP is the basis of search for ‘the maximum common substructure’ in the graph describing the chemical compound structure. Moreover, MCP is a mathematical model for multiple problems linked with automation of electronic equipment engineering. Generally, the applications mentioned above, require exact solutions for MCP. And the input data volume is enormous (input graphs can contain up to a million of vertices). Thus, current research direction MCP is a development of new approaches towards finding exact solutions considering peculiarities of graphs in applications. The maximum clique problem for undirected graphs is one of the combinatorial NP-complete problems. Generally, there is no polynomial algorithm for the problem [1]. And a great number of articles are dedicated to the problem [2]. All algorithms for solving MCP are classified into exact and approximate. The exact algorithms function, at the worst, during the time in exponential dependence on the input data volume. Clique-based algorithms (e.g., Cone [3], Burstall [4] and Raymond [5]) and backtracking algorithms (e.g., McGregor [6] and Wong [7]) are singled out among exact algorithms. Genetic algorithms [8] and combinatorial optimization algorithms [9] are singled out among the approximate ones.

The best known algorithms for finding the exact solution of MCP are the Bron-Kerbosh and the Wilf algorithms. The Bron-Kerbosh algorithm is a recursive procedure which upgrades a current clique considering one vertex at each step. The algorithm adds this vertex to the clique or includes it to the set of excluded vertices (which cannot be included in the clique). It is demonstrated, that the running time for the Bron-Kerbosh algorithm is O ( poly ( n ) ■ 3 n ³ = O ( poly ( n ) - 1.4422 ⁿ , where poly ( n ) is a polynom of n =| V | . The Bron-Kerbosh algorithm has repeatedly been perfected. The fastest modification of the algorithm finds an exact solution of MCP        in         a        time         of

O(poly(n) ■ 20,249n) = O(poly(n)-1.1888n  ). The Wilf algorithm is also a recursive procedure. However, it finds not the maximum clique, but the largest independent set of vertices of the graph. It has been demonstrated that the running time for the Wilf algorithm is O (poly (n)-1.39n)   O (poly( n )-1.39 n).    Among the approximate methods of solving the МСР, it is possible to single out papers [10-13]

II. Basic Concepts And Definitions

Let G = ( V , E ) be an undirected finite graph with the vertices V and the set of edges E , | V |≥ 1 and | E |≥ 0. The set of all vertices of the graph G, adjacent to the vertex x ∈ V , forms in g the environment of the vertex x specified by N ( х ). The set of vertices V ^| ⊆ V is called a clique of the graph G if in the graph G ( V^| ) any two vertices are adjacent, and a maximal clique, if it is not included in a clique of larger number of vertices. The size of the largest clique (by number of vertices) of the graph G is specified by ϕ ( G ) and called the density (or the clique number) of the graph G . The graph G = ( V , E ), which is a clique, is called a complete graph and specified by Kn, where n = | V | . For it ϕ ( K ) =| V | . Generally, for the graph G = ( V , E ) always 1 ≤ ϕ ( G ) ≤ | V | . The subset V ^| ⊆ V is assumed independent in the graph G = ( V , E ) if the subgraph G ( V^| .) does not contain edges. The largest independent set in terms of size is called maximal. The number of vertices in the maximal independent set is the independence number of the graph G designated by α ( G ) . The independence number of the graph G and density of the complementary graph G are connected by the formula: α ( G ) = ϕ ( G ) , ϕ ( G ) = α ₀( G ) . The identification variant of MCP can be formulated as follows.

STATEMENT. Given the graph G = ( V, E ) and the positive number K ≤ | V | .

QUESTION. Is it true that G contains a clique of the size exceeding K ? Otherwise, is there the subset V ^| ⊆ V , so that | V ^| | ≥ K and any two vertices in V' are connected with an edge from E ?

It is easy to demonstrate that the presence of an independent set of the size exceeding K in a complementary graph is the necessary and sufficient condition for existence in G a clique of the size K. Thus, knowing an exact solution about the problem of an independent set of vertices, it is possible to specify an exact solution to MCP and vice versa.

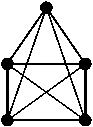
5          4

Fig.1. Graph G

III. Formalization and Problem Solution

Let us consider the triangle decomposition of a graph by an example of the complete 5-node graph G (Fig.1) and build a triangle on the base of each edge ( i, j ), and the vertex number i is always lower than the vertex number j . The triangles built are presented in Figures 2-5.

Fig.2. The set Ω of the triangles Δ built on the edges

( i = 1, j ); j = 2,3,4,5

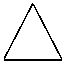
A

Fig.3. The set Ω of the triangles Δ built on the edges

( i =2, j ); j =3,4,5

Subsequently, triangles will be specified by three figures indicating numbers of triangle vertices, for example, the first triangle A .=1 in Fig. 2 is specified as 123, where (12) is the edge on the base of which the triangle with the vertex 3 is formed. In Figures 2-5 the triangles which duplicate the triangles already build are highlighted and will be removed. Thereafter, the following triangles will remain and they are presented in Table 1.

Table 1.

Set Q,.=1	Set Q ,	Set Q .
of the triangles	of the triangles	of the triangles
ACT = 1	A„ Q —2	A a = 3
123   134   145 124   135	234       245 235	345

The sets Q_z , as is seen from Table 1, are triangle subsets, in which we will distinguish the lines S (Q_z) and columns H _p (Q_z) . So, for example, in the set Q_z_! the triangles 123;134;145 form the first line S _j=[ = (Q_z [) of the triangle set Q_z_! , triangles 124;135 form the second line S _j=2 = (Q_z ]) and the triangle 125 forms the third line S _j=3 = (Q_z ])of the triangle set Q!. It is easy to note that if the size of a clique is n , the number of lines is X = n — 2 in Q! . The first column H_{p =1} (Q_z [) in the set Q_z=1 is formed by the triangles 123;124;125, the second column H p = 2 ( fi i = 1 ) is formed by the triangles 134;135 and the third column H _p _₃(Q_z_₃) is formed by the triangle 145, their number ф is also equal to n — 2 . When the number i increases by a unit of the set Q_z the number of lines and columns also decreases by one. If the set of all triangles of the set Q_z is recorded in accordance with their record in the columns Q_z , we can say that the ordered set Q_z is specified. Thus, the ordered set Q_z j (Table 1) is as follows

Qz=1 = {123;124;125;134;135;145}

Define the general number of various triangles for the case when a complete graph has n vertices. Specify the maximum number of triangles with the edge (1,2) by k , generally k = n — 2 .Therefore, the general number of various triangles, which can be built in a complete graph is equal to the sum of the following lines.

z = (1 + 2 +... + k) + (1 + 2 +... + k — 1) +

+ (1 + 2 +... + (k — 3) +... +1)              (1)

Present the sum (1) as the following triangle for n = 5 and k = n — 2 = 3

1 + 2 + 3 = 6

1 + 2 = 3 1

the sum is 10

It follows from the triangle that for the arbitrary k, if summarize the lines defined by relation (1) we form k ones, k — 1 twos, k — 2 trees, k — 3 fours, etc., that is the sum (1) can be presented as z = 1 k + 2(k — 1) + 3(k — 2) + 4(k — 3) + 5(k — 4) +... (2)

Rewrite (2) as follows z = (k + 2 k + 3 k + 4 + 5 k +...) — (2 -1 + 3 ■ 2 + 4 ■ 3 + 5 ■ 4 +...) =

= k (1 + 2 + 3 + ... + k ) — [(1 + 1) - 1 + (1 + 2) ■ 2 + (1 + 3)3 + (1 + 4)4 + ... =

= k (1 + 2 + 3 + ... + k ) — [(1 + 2 + 3 + ... + k — 1) + (1 2 + 2 2 + 3² + ... + ( k — 1) 2 ]

By considering

(1 + 2 + 3 +... + k) = k (k +1);

1 2 + 2 2 + 3 2 + ... + k ² = k ( k + 1)(2 k + 1)

we will have к2^-1

z = - [ k ( k + 1) — ( k — 1)(1 + —)]

by substituting k = n — 2, finally we get z = (n^) {(n — 2)( n — 1) — (n — 3)[1 + 2n—5 ]} =

2                                3

n (n —1)( n — 2) =

Check it and suppose n =5, so we will get the unknown quantity equal to 10.

5 ■ 4 ■ 3

z =-----

= 10

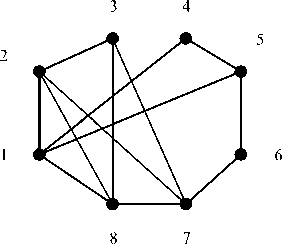
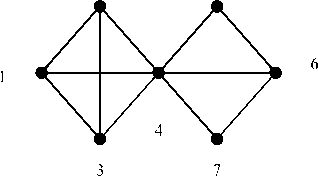
Fig.6. Graph G

Among the triangles the duplication triangles A . are highlighted, and after their removing, we will obtain the set {A_ct } ={128;154;237;278;238;451;56;67;783} with z = 7 various triangles A_ct and z^ =2 edges. Some edges appearing in the process of decomposition of a graph, which cannot be the base to build triangles in the clique search, can be removed. It should be noted that the union of triangles A_ct in subsets Q_; allows each to generate the largest clique Q .Choosing among them a clique of maximum dimension, we get the largest clique in the analyzed graph. This expansion will be used later to determine the maximum clique in arbitrary graphs.

The given characteristic of decomposition will further be used for determination of the maximal clique in arbitrary graphs. Decomposition of the graph, presented a clique, into triangles based on each edge ( i,j ), in which the number of the vertex i will always be lower than number of the vertex j , creates the triangle subsets {Q_;} which will be presented orderly hereafter. In an arbitrary graph when forming subsets among triangles, the union of which gives the maximal clique with the vertex i, there exist triangles not belonging to the given clique. They can be formed by joining the clique by separating vertices or built on the edges the clique (Fig.8). The vertex is called separating if its removal increases the connectivity component number in the graph.

If a graph is incomplete, it decomposes into the triangles A_ct and edges, as there may appear edges on the base of which it is impossible to build triangles. For example, for the graph G presented in Fig.6 decomposition into triangles and edges is as follows: A,={128;145;154;237;278;281;238;372;56;67; 783}.

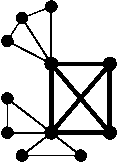
Joining the triangles to the clique through the separating vertices vertices

Joining the triangles through the clique edges

Fig.7. Alternatives of joining the triangles to the clique of 4 and 5 vertices

Thus, a set of triangles in the subsets Ω can be divided into two subsets { Δ ^γ } and { Δ ^* } , where { Δ ^γ } is the set of triangles, the union of which forms in Ω the maximal clique Q ^max of the size γ ; { Δ ^* } is the subset of triangles linked to the clique Q ^max . With respect to the two subsets the following statements are true.

Statement 1. If in the subsets Ω there exists Q of ii the size P(Q ) on the set of vertices belonging to the triangles Δ , so there exists the union of triangles Δ ∈ {Δγ } which forms the given clique Q .

The trueness of this statement results from the triangle decomposition of a graph considered.

Statement 2. The union ∪ Δ of the arbitrary triangles Δ ∈ { Δ ^γ } forms a complete subgraph.

Let the union ∪ Δ of triangles form the clique Q of the size P(Q ) . If we consider the union of two triangles Δ and Δ , so that the union of the given triangles forms the complete subgraph, the set of all vertices of the first triangle should be linked with the set of vertices of the second triangle. It is obvious that the triangles forming the clique should satisfy the given characteristic. Suppose that there is the triangle Δ* ∈ {Δγ } which by joining the triangle Δγ forms an incomplete graph, i.e., if we unite all triangles there will be at least one vertex not connected to all vertices, that is, the clique size is P(Q ) -1, which contradicts the assumption about the existence of the clique Q of the size P(Q ) . The following consequence from the statement 2 is important.

Consequence. The union of the triangle Δ* ∈ {Δγ } and the union ∪ Δ of the

Δ ∈ {Δγ } lead to formation subgraph.

Therefore, if we unite two arbitrary triangles of an incomplete

arbitrary triangles

Δγ ∪ Δγ from the set {Δγ } , we will obtain a complete subgraph, and if we unite pairs of triangles Δ* ∪ Δ* from the subset {Δ* } or various substes Δγ ∪ Δ* we will obtain incomplete subgraphs. It is obvious, that an arbitrary union of triangles of the arbitrary subset of triangles Δ ∈ {Δγ } always forms an in complete graph. As the vertex enumeration in the graph under consideration is random, the maximal clique can be placed in one of the subsets Ω , a set of triangles being in any of the subsets. In order to define the maximal clique in the graph under consideration, firstly, we need to find such unions of the triangles {∪Δ } which form the maximal cliques Qmax in the subsets Ω , and, then, choose the maximum clique Qi = max{Qmax } . Consider the formation of Qmax from triangles of the subsets  {Δγ } ∈ Ω and

{ Δ ^* } ∈ Ω . i n terms of formation of cliques of triangles consider the following most important cases of unions of triangles in the subsets Ω for formation of Q ^max :

• 1.    The triangles forming Q ^max in Ω do not cross the triangles forming other cliques in the graph G or there exist intersections only through separating vertices.

• 2. The triangles forming Q ^max in Ω intersect the

• 3. The triangles forming Q ^max in Ω intersect the

triangles not belonging to any other clique of the graph G.

triangles forming other cliques in the graph G of the size P ( Q i ) ≤ P ( Q i ^max) .

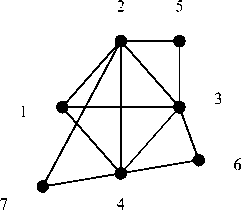
Examples of the graphs corresponding to Cases (1-3) and their ordered sets Ω are presented in Table 2.

As is seen from Table 2, in Cases 1 and 2 there always exist the subsets Ω only with the triangles forming Q ^max , in Case 1 such subset is Ω = {123;124} , and in Case 2 it is Ω = {123;124;134} . In Case 3 the subset

Ω = {123;124;125;127;134;135;145;157} contains both the triangles {Δγ } ={123;124;125;135;145} belonging to Qmax and the triangles {Δ* } ={127;157} not belonging to the given clique. It raises the question about how Qmax can be formed from subsets of the triangles {Δγ } ∈ Ω and {Δ* } ∈ Ω . Therefore, take Statement 2 and the consequence from it, implying that if we unite two arbitrary triangles Δγ   ∪ Δγ   from the set {Δγ } , we will obtain a complete subgraph, and if we unite pairs of triangles Δ*   ∪ Δ*   from the subset

{Δ* } or various substes Δγ   ∪ Δ*   we will obtain incomplete subgraphs. Start the building of Qmax with enumeration of the triangles Δ ∈ Ω ;. i = (1, q) from 1 to t. The number t of the triangles Δ in Ω cannot exceed the valueη = (n - 1)(n - 2) . At t=5 the triangle sets T is of the form (Table 3).

Table 2

2               5

• Case 1

Q_M = {123;124} ; Q. = {234}

Q_i4 = {456;467}

Q i = 3 = Q i = ₅ = Q i = ₆ = Q i = ₇ = 0

Q_/=1 = {123;124} ; Q. = {234}

Q_/=5 = {567;568} ;

Q = Q 6 = Q, 7 = Q, 8=0

i 4           i 6           i 7           i 8

• Case 2

Q_M — {123;124;134} ; Q_₽2 — {234;235;247} ;

Q i — 3 — {346}

Q i — 4 = Q i — 5 = Q i — 6 = Q i — 7 = 0

• Case 3

  
  
  

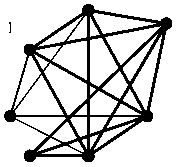
Q_M — {123;124;125;127;134;135;145;157}

Q_/=2 — {234;235;245;247;257}

Q_₽3 — {345;346;356}

Q i — 4 — {456;457}

Q i — 5 = Q i — 6 = Q i — 7 = 0

Table 3

T To — 1	T T o — 2	T o — 3	T T o — 4	T o — 5
1 2 3 4 5	2 3 4 5	3 4 5	4 5	5
1 3 4 5	2 4 5	3 5	5
1 4 5	2 5	5
1 5	5
5

The triangle set T allows us to define all possible unions of triangles based on the triangle with the number o ; o — (1, t ) which give complete graphs in the union. Each triangle of the set contains j lines, where j — (1, t ) . So, if the set of triangles {A_CT=1; A_CT=2 ;... A } G Q_; contains t triangles, then the first line of the triangle set T also contains t triangles. Consider unification of triangles by example of this line; the unification of triangles in other lines runs similarly.

Procedure B of triangle unification of j-line in the triangle set T

Choose the triangle Δ ∈ Ω in j -line out of the triangle set { Δ    ; Δ ;... Δ } and form the union

Δ ∪ Δ which creates a subgraph (complete or incomplete). If the graph is incomplete the union ^Δ σ = 1 ^{∪ Δ} σ = is marked with (-) and the triangle Δ is skipped, the union with the next triangle Δ is checked and union Δ ∪ Δ ( + ) is marked with (+). Consider the union Δ ∪ Δ ∪ Δ (+) and it gives the complete subgraph, then consider the union Δ ∪ Δ ∪ Δ ∪ Δ (+) , that is, all triangles of the union belong to the subset { Δ ^γ } and it also gives the complete supgraph, then consider the union Δ ∪ Δ ∪ Δ ∪ Δ ∪ Δ    (-), i.e. the

σ=1      σ=3      σ=4      σ=5      σ=6    , triangle Δ ∈ {Δλ } , skip it and begin forming the next union Δ ∪ Δ ∪ Δ ∪ Δ ∪ Δ and σ=1      σ=3      σ=4      σ=5      σ=7

repeat the procedure. After formation of all possible unions with the 1^st triangle in j -line, select the union with the maximal clique Q ^max , defined by unification of all triangles belonging to { Δ ^λ } . i f Δ ∈ { Δ ^* } and all its unions give incomplete graphs, Q ^max is the empty set {0}.

By applying procedure B to all lines of the triangle sets { T } , form the sets { Q ^max } based on the lines of triangle sets and select among them the maximal clique Q m ^σ ax = max{ Q ^m j = ^a1^x ; Q ^m j = ^a2^x ,..., Q ^m j = ^a t ^x } obtained on the base of j -line of the triangle set T . Having formed the set of cliques { Q ^σ } for all triangle sets { T } and selecting among them the maximal clique Q i ^max =max{ Q m ¹ ax ; Q m ² ax ;...; Q m ^t ax } we obtain the maximum clique in the subset Ω . Further, we can similarly determine the cliques Q ^max for the other subsets Ω ; i = (1, q ) and among the subsets of cliques { Q ^max } ; i = (1, q ) select the maximal clique Q = max{ Q ^max } and it turns out to be the maximum clique in the graph G. Thus, we can propose the following procedure A for determination of the maximal clique in an arbitrary graph.

Procedure A

Step 1. Form the ordered subsets of triangles Ω based on the edges of a graph beginning with the vertex of a lower number on the edges ( i, j ) on condition that i >  j and pass on to the next step.

s tep 2. f orm the triangle sets { T } in the ordered subsets Ω and, by applying procedure B to all lines of the triangle sets { T } of the subsets Ω , form the sets { Q ^max } on the lines of the triangle sets and select among     them     the      maximal      cliques

Q ^σ max =max{ Q ^m j = ^a 1 ^x ; Q ^m j = ^a 2 ^x ,..., Q ^m j = ^a t ^x } and pass on to the next step.

Step 3. Among the subset of the formed cliques { Q ^max }      choose     the     maximal     clique

Q = max{ Q ^max } and the procedure finishes.

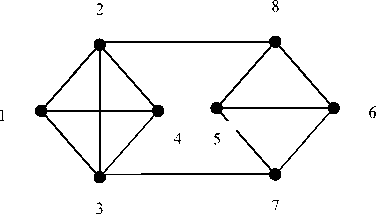
Consider an example of the procedure for the graph G presented in Fig.8.

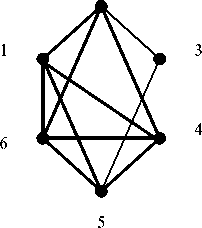
Fig.8. Graph G

Form the subsets Ω for the given graph, their form is

Ω = {124;126;145;146;156}

Q _г = 2 = {246} ; Ц = 3 =0;

Q 4 = {456} Q , = ₅=0; Q _г = ₆=0;

Renumber the triangles in the subset

Ω = {124;126;145;146;156} (Table 4).

Table 4 Triangle number      1      2        3         4       5 124    126      145     146    156 {Δσ}∈Ω =1 form the triangle sets {T } and apply to them procedure B to unite the triangles (Table 5)

Table 5

T }

^T 1 1 2 3 4 5

Procedure B

112 +;123 -;124+;1245-; obtained the maximal union of triangles 124; the union of these triangles formed the complete subgraph on the vertices of united triangles, i.e. obtained the clique q™ ={1246}

1 3 4 5	13-;14+;145-; obtained the maximal union of triangles 14 and obtained the clique Q max ={1246}
1 4 5	14+;145-;obtained the maximal triangle union 14 and obtained the clique Q max ={1246}
1 5	max 15-; obtained Q j = 4 =0
5	max Q j 5 ={156}
T T 2 2 3 4 5	23-;24+;245-; obtained the maximal union of triangles 24 and obtained the clique Q max ={1246}
2 4 5	24+;245-;obtained the maximal triangle union 24; obtain the clique Q max ={1246}
2 5	89-; obtained Q max =Ø
5	max Q j = 4 ={156} T 3
3 4 5	34+;345; obtained the maximal triangle union 345; obtained the clique Q max ={1456}
3 5	35+; obtained the maximal triangle union 35; obtained the clique Q max ={1456}
5	Q ” ™ 4 ={156}
4 5	T 4 45+; obtained the maximal triangle union 45; obtained the clique Q max ={1456}
5	Qv ma2 ={156} T 5
5	Q m j ax 1 ={156}

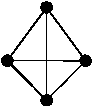
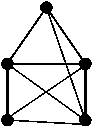
For instance, the triangle union 1 О 2=124 О 126 gives a complete subgraph (Fig.9a), and the triangle union (Fig.9b).

1 О 2 О 3 =124 О 126 О 145 gives an incomplete graph

а)

b)

Fig.9. The subgraphs obtained by uniting the triangles 1,2,3.

Then, determine Q ^max = max{1246;1456;156}=1246 or 1456; Q_i ^m ₌ ^a ₂ ^x = {246} ; Q_i ^m ₌ ^a ₄ ^x = {456} , hence Q = max{1246;1456;356;456} =1246 or 1456, i.e. the maximal clique is found and in this case there are two of them 1246 and 1456

• IV. Assessment of Complexity and Efficiency of Procedure a

Formation of the triangle subsets Ω is on the edges (i, j) incident to the vertex i , the number of edges incident to the vertex i cannot exceed n -1 , and the number of triangles to be built on one edge cannot exceed n - 2, therefore, the general number of triangles in the subset Ω do not exceed h = (n - 1)(n - 2) < n 2 , the number of the sets Ω is q ≤ n - 1 . Consequently, the general number of triangles to be built in procedure A does not exceed (n - 1)2 (n -2) ≤ n3 , taking into account that forming one triangle consists of less than 2n comparison operations, procedure A takes less than 2n 4 comparison operations to form the subset Ω .

Thereupon, procedure B begins to run in the subsets Ω and analyses the triangle sets T ;T   ;...T    , determines the number of unions for analysis to form the maximal clique. The most labour-intensive is the analysis of the first triangle set with the number of lines t equal to h. And the first line T also contains h triangles. The number of lines and operations of unions in a line is given in Table 6.

• Table 6.

  Triangle sets

  т

  σ = 1

  т

  T σ = 2

  т

  σ = h - 1

  т

  σ = h

  
  

Number of unions h ( h - 1)

2 ( h - 2)( h - 3)

^… 2

Table 6 demonstrates that the number of unions is determined by the sum of the following sequence 1 ₊ 2 _{+ ... +} h _- 1 ₌ ^{h ( h - 1)} . Similarly, the other triangle ...                   ₂

sets are presented in Table 7 which shows that the number of unification operations to analyze all triangle sets cannot exceed 0.5 h ²( h - 1) <0.5 h ³ .

• Table 7

Triangle numbers              Number of unions

1    2   3    …       h    h -1

• 1   3   …       h h _-2

…  …h -1   …h   2… h 1

l ess than 2 n comparison operations will be needed so that to establish the fact whether the subgraph complete or incomplete while uniting the triangles, and h does not exceed n ² . Consequently, considering the fact that we have to select the maximal element in the massif of the size not exceeding h, the general number of comparison operations in procedure B with triangle sets is equal to 0.5 h ³ ⋅ 2 n + h log h = n ⁶ + 2 n ² log n ≈ n ⁶ .Thus, for a maximal clique in one triangle set Ω less than n ⁶ comparison operations are required. As the number of subsets Ω cannot exceed n - 1 and we need to select the maximal element out of the massif of numbers not exceeding n - 1 , the general number of operations in procedure A does not exceed n ⁶ ⋅ ( n - 1) + ( n - 1) log( n - 1) ≈ n ⁷ . As procedure B performs an implicit complete search for triangle unions which can lead to complete subgraphs, procedure A always gives the exact solution.

• V.    Experimental Research of Procedure A

During the experimental research more than 50 problems were generated at each point. The confidence probability of the findings obtained was 0.95, the edge density in the graph changed from 0.3 to 0.6, the edge density of the graph was evaluated by the relation m

ρ =       , where m is the number of edges in the

Е max complete graph G(V,E), and E = n(n - 1) is the maximum possible number of edges in the graph G(V,E) with n-vertices. The numbers of vertices in the graph changed from 10 to 150, the edges were generated by the distribution uniform law. The range of parameters ρ and n is conditioned by the possibility to check the accuracy of the solutions obtained, since when ρ works for one, the procedure complexity works for the upper mark O(n7 ) and if n is more than 20 and the density is ρ =0.89, it is almost impossible to check the accuracy of solution. Validation of the developed problem-solving procedure when analyzing the graph G was based on building the complementary graph G . Then all maximal independent sets for the graph G with the algorithm from [14] were enumerated. Furthermore, the following was checked: whether the size of the maximal clique obtained in procedure A equal to the size of the greatest maximal set in the graph G . If it is coincident, we can conclude that the problem is true. The verification did not reveal any inexact solutions. The findings of the experimental research are demonstrated in Tables 8-11. In the Tables the parameter α is the average general number of various triangles built in procedure A; λis the average size of the maximal clique built in procedure A; EO is the average number of elementary comparison operations in procedure A; t is the average time of procedure A in seconds; m is the average number of edges in the graph.

Table 8

n = 40	Dependencies of average number of elementary comparison operations (EО), time of triangle formation ( t ) and their number α ,as well as average value of time complexity in building various triangles on the density of edges ρ in the graph
ρ EО t (sec) α	0.1          0.2          0.3          0.4          0.5          0.6          0.7          0.8          0.9          1.0 700       2423       5140       8340      12933      17498      22973      28675      35442      42640 0.013        0.1          0.3         0.85         1.56        2.65        4.29        6.49        9.73        14.54 7         67        232        655       1232       2116       3382       5040       7219       9880
O ( nx )	1.8             2.2             2.6             2.6             2.6             2.7             2.8             2.8             2.9             2.9 n       n       n       n       n       n       n       n       n       n

	Table 9 Dependency of the average value: operations executed in procedure A (EO); time of
ρ =0.3	procedure A ; number of triangles built α ; dimensions of maximal cliques λ ; number of edges of the graph
n EО t (sec)	30              50               80              100             150 5463           74961          1474957        9401679       114473122 0.09              0.2               1.58              8.81             103.48
α λ m	96             489            2202           4316           14858 4                 5                 6                 6                 6 130             367             948             1485            6352

Table 10

Dependency of the average value: operations executed in procedure A (EO); time of

procedure A; number of triangles built α ; dimensions of maximal cliques λ; number of ρ =0.5                                          edges the graph

n	10	20	30	40	45
EО	345	49928	1229337	95765414	781267305
t (sec)	0.02	0.14	1.97	136.5	911.6
α	13	142	487	1203	1754
λ	4	5	7	8	8
m	22	95	217	390	495

Table 11

ρ =0.6

Dependency of the average value: operations executed in procedure A (EO); time of procedure A ; number of triangles built α ; dimensions of maximal cliques λ ; number of edges of the graph m;

n	15	20	25	30
EО	49928	1229337	95765414	781267305
t (sec)	0.14	1.97	136.5	911.6
α	142	487	1203	1754
λ	5	7	8	8
m	95	217	390	495

If the densities are in a range of 0.8-0.9, the complexity of procedure A is close to the upper value O ( n ⁷ ) . As the analyses of the subsets Ω and triangle sets { T } can be fulfilled independently, procedure A can be efficiently parallelized which allows solving problems for graphs of great densities in real time.

• VI.    Inference

Thus, for the first time a polynomial algorithm of the problem of maximal clique solution was built. Although the polynomial degree is rather high, the fact that a polynomial algorithm exists is more important for solving the task. As far as the task is one of the class NP-complete problems, the result obtained needs considerations. The existence of an algorithm of polynomial complexity considered in the study for determination of the maximal clique does not equalize the classes P and NP, whereas, as study [15] shows, Cook’s theorem on the concept of NP-completeness of SAT is false. Study [15] puts forward the hypothesis that the existence at least one NP-complete problem is algorithmically unsolvable and the whole set of problems of discrete optimization and theory of graphs can be divided into subsets, in which one problem can be reduced to another polynomially. In such problem subsets the solution of one problem with the help of a polynomial algorithm leads to existence of the polynomial solution algorithm for the whole subset. But the question of polynomial transformation of problems for one such a subset into problems of other subsets is not solved. In this context such a subset forms problems as SAT and also the following: determination of graph isomorphism, determination of isomorphic embedding of a graph, determination of maximal independent sets and minimal vertex cover of graphs, as well as schedule feasibility, as they can easily be reduced to MCP in polynomial time.