An approach to develop a transactional calculus for semi-structured database system

In recent years, researches have produced several proposals [2, 3, 4, 5, 7, 8, and 9] towards conceptual modelling of semi-structured database system compare to the proposals of conceptual modelling. To overcome traditional transactional problems, extending the transactional processing system in semi-structured database by addition of compensation and coordination of consistency, availability, and partition tolerance (CAP)[12] and basic availability, soft state and eventually consistent (BASE) [45] theorem and enrich a standard design model with new healthiness conditions. There is no specific transactional calculus for semistructured data. The proposed Transactional Calculus for Semi-structured database (TCSS) puts forward a mathematical framework for transactions where a transaction is treated as a mapping from its environment to compensable program. Further, the transactional calculus is derive from an algebra based query language GQL-SS [11] and illustrated using examples of real life. The motivation of the Transactional Calculus for Semistructured System, it is desirable to provide some amount of fault tolerance, on a highly distributed network. It is important that the service still perform as expected, when some nodes crash or communication links fail. The ACID (Atomicity, Consistency, Isolation and Durability) acronym says that database transactions should be firstly, seem indispensable, and yet they are incompatible with availability and performance in very large systems. The semi-structured database violates the ACID properties. According to ACID properties in Atomic the entire transaction will fail if one node element of a transaction fails, but in semi-structured database, it is not possible. In semi-structured database, if one node is damaged the entire network should not be affected. Secondly, no transaction has access to any other transaction in Isolation that is in an intermediate or unfinished state. Thus, each transaction is independent unto itself. This is required for both performance and consistency of transactions within a database. The semi-structured database violates this property because it works in path basis and every node is inter linked to each other. The benefits of the transactional calculus for Semi-structured databases are manifold. It provides supports towards (1) structural and functional design concerns with enriched semantics and syntaxes for transactional calculus of semi-structured database represented by precise knowledge of domain independent conceptualization;(2) a systematic methodology which used to transforming calculus for functional design; (3)Transactional Calculus to Semi-structured database query system provides guidelines for the purpose of mapping .The proposed Transactional system for semi-structured is based on path expression. The path expressions may also contain label variables to preserve labels or tags. Three types of algorithms are using to evaluate the path in Graph Object Oriented Semi-Structured Data Model (GOOSSDM)[2, 19, 20, and 21] schema and Graphical Query Language for Semi-structured (GQL-SS) [11] schema, one for searching return node, second for searching the path from root of GOOSSDM schema to the desired node and the third one is for the searching and listing of the tail nodes.. Here trying to use the CAP theorem in the broader context of distributed computing theory. An important contribution of this paper is to discuss some of the practical implication of CAP Theorem of a transactional calculus for Semi-structured database. There are some proposal; they are only using CAP [12] or BASE [25] theorem or without these. To introduce the transactional calculus for Semi-structured database, with the help of CAP theorem, the CAP theorem was introducing as a trade-off between consistency, availability and partition tolerance. Consistency: A read sees all previously completed writes i.e. all nodes see the same data at the same time. Availability: A guarantee that every request receives a response about whether it succeeded or failed i.e. read and write always succeed. This means that in GOOSSDM schema there should be a searching path and its return some value. The path value should not be null. Partition Tolerance: Guaranteed properties are maintained even when network failures prevent some machines from communicating with others. The system continues to operate despite arbitrary partitioning due to network failures.

However, developers face some challenges despite of several advantages of existing Semi-structured databases, when they apply the transaction processing system. Such challenges are as follows-

Ch1: Lack of transactional methodology that blends semi-structured databases specification with syntaxes of transactional calculus for semi-structured database system.

Ch.2: Majority of existing transactional procedure are not usable for large semi-structured database queries.

Ch.3: Few transactional calculus for semi-structured database approaches are present in literatures that may represent evolving knowledge of transaction in semistructured databases but not in precise.

Ch.4: Appropriate guidelines and tools are absent which may help designers for specification.

Ch.5: XML-based semi-structured database systems characterized by an expressive global schema. The main issue here concerns the presence of a significant set of integrity constraints expressed over the schema and the concept of node identity, which requires particular attention when data come from autonomous data sources. This paper fulfils the deficiency of systematic methodology in transactional calculus of GOOSSDM model[44]. The paper is structuring as follows. Several related works in this field specified in Section 2 briefly. Section 3 is about the GOOSSDM modelling framework and this portion is subdividing into two parts components of GOOSSDM and Illustration of GOOSSDM. The proposed Transaction calculus for semi-structured database system (TCSS) has been describing and formalised in Section 4. Next, guidelines about the way in which the validation of TCSS can be applied databases by using CAP and BASE theorem and application specific conceptualisations have been suggesting in Section 5. Further, the proposed TCSS have been implementing and visualised using different operators and practically illustrates the proposed work using suitable example in Section 6. Following this, Section 7 practically illustrates the proposed work using a suitable programming code. Finally, the paper is concluding in Section 8.Aiming to overcome issues explained in above mentioned challenges this paper proposes several objectives. First, the proposed framework of Transactional system for semi-structured is based on path expression. They may also contain path variables, which, are evaluating to the empty path or to a path having a length of n edges. The path expressions may also contain label variables to preserve labels or tags. At second, the path operator is using to set the root node in GOOSSDM [2, 19, 20, and 21] schema and useful to find the path from the root node to desired node for any transaction. At Third, the propose work facilitate the early verification of the semi-structured data schema structure in correspondence with the desired transactional calculus. Finally, the transactional calculus is introducing to Semistructured database, with the help of CAP and BASE theorem. This objective addresses the issues described in Ch.2,  Ch.3, Ch.4 and Ch.5.The benefits of the

Transactional Calculus for Semi-structured system will represents a framework for specifying the semantics of a transactional facility integrated within a Semi-structured database system. The motivation of the Transactional Calculus for Semi-structured System is-finally, on a highly distributed network, is that when some nodes crash or communication links fail, it is important that the service still perform as expected. This paper fulfils the deficiency of systematic methodology in transactional calculus of GOOSSDM model. In addition, this paper proposes a formal transactional calculus called

Transactional Calculus for Semi-structured database (TCSS) in terms of concepts, relations and axioms for domain independent systems. It provides syntaxes and semantics for TCSS. Further, the transactional calculus is derived from a algebra based query language GQL-SS [11] and illustrated using examples of real life. Moreover, TCSS are proved by CAP and BASE theorems properties to show the expressiveness of the propose calculus.

• II.    Related Work

In previous work [11], focused on path expression in semi-structured database system. More precisely (i) described GOOSSDM [2,19,20 and 21] schema and GQL-SS [11] data are amalgamate to leaves so the path expression may carry data variables as abstractions of the content of leaves. They may also carry path variables those are evaluating to the void path or to a path having a length of n edges. The path expressions may also contain label variables to preserve labels or tags. (ii) Develop three types of algorithms. Three types of algorithms use to evaluate the path in GOOSSDM schema, one for searching return node, second for searching the path from root of GOOSSDM schema to the desired node and the third one is for the searching and listing of the tail nodes. (iii) Define the GQL-SS algebra for GOOSSDM model that operate on semi-structured schema concept and / or several constructs described in the model. The algebra consists of a set of operators and few of them can be using with the constructs like ESG, CSG separately.

As a result, point out that have to develop a transactional calculus related to this GQL-SS model. To the best of knowledge, there are no other global solutions addressing the transactional calculus for semi-structured database system. A small number of research works exist in the literatures those are in general semi-structured and used query language. However, still there is no specific transactional calculus, which is devoted enough to conceal the five challenges specified in the introduction section. The work in Supporting Multi Data Stores Applications in Cloud Environments [23] has given some idea about the semi-structured query but no proposed calculus. The amalgamation of transactions with programming control structures has provenance in systems such as Argus [28, 29].There is a composition of work that enquire into the formal specification of various zest of transactions [35, 36, 37]. However, these act of striving do not explore the semantics of transactions when integrated into a high-level programming language. Most closely related to goal is the work of Black et. al. [38], Choithia, and Duggan [39]. The former presents a theory of transactions that specify atomicity, isolation and durability properties in the form of an equivalence relation on processes. Beyond significant technical differences in the specification of the semantics, results differ most significantly from theirs insofar as [6] present a stratified semantics for a realistic kernel language intended to express different concurrency control models within the same framework. Choithia and Duggan present the pik-calculus and pike-calculus, extension of the pi calculus that supports various abstractions for distributed transactions and optimistic concurrency. Their work is relating to other efforts [40, 41] that encode transaction-style semantics into the pi-calculus and its variants. Haines et.al. [31] describes a compassable transaction facility in ML that supports persistence; undo ability, locking and threads. Their abstractions are modular and first class, although their implementation does not rely on optimistic concurrency mechanisms to handle commits. Consequently, none of the existing approaches is appropriate enough to cover the 5 challenges specified in the introduction section. In this regard, devising a new proposal, which is essential to resolve the issues, addressed in the 5 challenges.

In this case, since dealing with the combination of CAP and BASE theorem, this proposal for expressing and executing queries and real time applications shown by using the calculus. Introducing an approach for a mapping language to map attributes of the data sources to the global schema and bridge query language to write the calculus.

• III.    Goossdm: The Basic

Extending the object-oriented paradigm to semistructured data model, the GOOSSDM introduced. It’s specifying the irregular and heterogeneous structure, hierarchical and non-hierarchical relations, n – array relationships, cardinality and participation constraint of instances with all details that are required for semistructured data model. The entire semi-structured database to be viewing as a Graph (V, E) in layered organization that is allowed by the proposed data model (GOOSSDM).At the lowest layer, each vertex represents an occurrence of an attribute or a data item.

Let consider an example of Project Management System (PMS),[11], associated with Project. Project has attributes like members, department and publications. Several members are associated with project and each member can participated in any project. Department contains member, and each individual members may have or not have publication. The PMS is semi-structured is in nature. The GOOSSDM schema for PMS has been shown in fig. 1. The sample data is showing in Table 1.

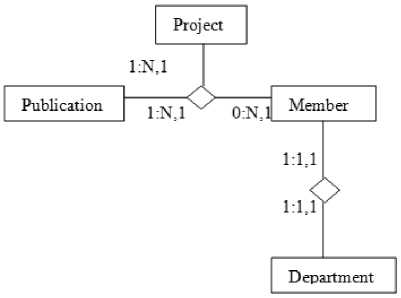
Fig.1. GOOSSDM Schema for PMS

Table 1. Sample Data Set for PMS

Project 1
Pname	PID	Topics	Member			Department		Publication
			MID	MName	Maddress	DID	DeptName	PuID	Ptopics
ABC	P1001	AAAA	M01	Bipin	XX	D01	CSE	P001	RRR
XYZ	P1003	CCCC	M03	Ashu	PP	D02	CA	P003	SSS
DEF	P1004	DDDD	M04	Rashi	YY	D03	EE	P004	TTT
XYZ	P1005	QQQQ	M06	Sashi	RR	D03	EE	P005	VVV
ABC	P1001	BBBB	M07	Priya	CC	D01	CSE	P006	MMM
Project 2
Pname	PID	Topics	Member			Department		Publication
			MID	MName	Maddress	DID	DeptName	PuID	Ptopics
PQR	P1006	YYYY	M07	Priya	CC	D02	CA	P007	NNN

• IV.    Calculus for Semi-Structured Database System

In previous work, defining the GQL-SS algebra for GOOSSDM model that employ on semi-structured schema impression and / or various form reportein the model. Using GOOSSDM schema the semi-structured data seen as single rooted or multi rooted graph. In every case, while initiating any query, one needs to set an immediate root for the desired CSG and then need to find the tail nodes in respect to the desired CSG.

In all the algorithms, the searching node and return node must be a type of CSG in GOOSSDM semantics. The GOOSSDM schema will use as input for the algorithms. The algorithms will invoke when the path operator (ρ) will execute. In case of proposed calculus whenever any operator will invoke, internally it will also invoke the path operator (ρ) to set the path from root node to the desired node in GOOSSDM schema by invoking algorithm 1 and algorithm 2. Moreover, the tail node list will create by invoking the algorithm 3 on next. If algorithm 1 and / or algorithm 2 return null value, then the actual operator need not to execute as there is no root available for the transactional calculus. This will facilitate the early verification of the semi-structured data schema structure in correspondence with the desired transactional calculus. The running example of Project Management System (PMS) used to illustrate the functionalities of operators. As specified earlier path operator (ρ) is also inclusive part of the algebra and invoked every time it is required to invoke any other operator specifically defined for management of semistructured data. In the example, if Project is set as root then the path from Project to Department can be established     and     expressed     as     Project

(Root) ^ Member ^ Department [11].

Algorithm 1: Searching of Node in GOOSSDM Schema

Step 1: Start

Step 2: Input a node C= (CSG).

Step 3: let op: = search node C

And return node C

Step 4: let P1:=layer 0

P2:= Immediate to layer 0

P3:= Next to immediate layer

P4:= Next to Next Immediate layer

Step 5: for i = 1 to 4

If (op P i (C) ≠ᴓ) then

Goto for next layer

Else

(Op P i (C))= (Root)

Step 6: stop

Fig.3. Searching path from root to desired node

Searching tail node from the desired node layer by layer, when the return operator of path is equal to the preceding one, then it is the last node i.e. tail node.

Fig.2. Searching tail node

Algorithm 2: Searching path from Root to Desired Node

Step 1: Start

Step 2: Input C=CSG // CSG for searching path.

Step 3: If (IS Root(C) =false) then

N1:=op P i (CSG, P, ϴ)

Step 4: If (N1==ᴓ) then

Path =N1

Else

Goto step 3.

Step 5: Exit

Root is Project, and then it searches the desired node layer by layer. Let N1is a path operator ρ with arguments layer no, CSG, and N1 value should not be Root. If N1 value is null, then the path value will be N1and if not then it will be check again from Root node.

Algorithm 3: Searching Tail Nodes from the Desired Node

Step 1: Start

Step 2: Input G=GOOSSDM schema

Step 3: let the path structured σ= (r,(E)), where E is a binary relation of(CSG,P,ϴ)

Step 4: For i = 1 to n                 // n= No. of iterations

If( IS Root(CSG))=True then

Op(CSG,P,ϴ)={CSGR,PR,ϴR}

Step 5: for i = 1 to n

Op< get the i^thnode>( CSG,P,ϴ)={CSG i ,P i ,ϴ i }

If( (op(CSG i-1 ,P i-1 ,ϴ i-1 ))== (op(CSG i ,P _i,ϴ _i))) then // Finding the Tail node

Tail =(CSG i ,P i ,ϴ i )

Else goto step 4.

Step 6 : The destination will be denoted as path ρ(CSG i ,P i ,ϴ i )= ρ{(CSG R ,P R ,ϴ R ), (CSG R-1 ,P R-1 ,ϴ R-1 ),( CSG R-2 ,P R-2 ,ϴ R-

2 ),.........,(CSG i , P i , ϴ i )}

Else goto step 3.

Step 7: Stop.

Fig.4. Searching tail node from the desired node

Searching tail node from the desired node layer by layer, when the return operator of path is equal to the preceding one, then it is the last node i.e. tail node.

• A. Propose Operator

In this section, the propose operator of Transactional Calculus for Semi-structured (TCSS) of GOOSSDM model is defined. It consists of a set of operators that take one or two CSG as input and produce a new list of CSG. The fundamental operators of TCSS consist of a set of operators and few of them also can be used with constructs like CSG, ESG separately.

• •    Select (σ) Operator

The select operator will select CSG and returns CSG that satisfy a given predicate of a given list of ESGs or CSGs from the GOOSSDM schema. Thus to select those CSG from GOOSSDM schema, the tuple relational calculus (TRC) notation may be write as,

[C| CeCS G }                  (1)

Its denote that tuple C is in CSG.

{ C IL is t( C)}                     (2)

Its mean, it is the set of all tuples C such that predicate list is true for C.

[ List (CSG) =OUTPUT CSG where list= {list of ESG} ]

If the set of all CSG for which the List(C) evaluates true. And the path expression will be like that-V i: 3 C:(,op p( i , C) = R о о t) [ for all levels, existential CSG set the path and if it does not have any edge then it is set to Root]

Pat h(R о о t, C)

Vi : Rоoi(,C") ^ (oppii , C))

Vi: (op p(i, C) ^ op p( i - 1, c - 1)) ^ dssired.(C).

[Searching for desired

CSG level by level and get ultimate CSG.]     (4)

• •    Retrieve (π) Operator:

The retrieve operation allows producing the CSG from GOOSSDM schema that satisfies a given condition. The retrieve operator extracts ESG or CSG from the CSG using some constraints CON over one or more ESG or CSG defined in GOOSSDM schema.

{C|VC1 e CSG(C 0)}[C [ C1 belongs to some CSG with satisfied condition]               (5)

It is meaning that the set of all tuples C such that for all tuples C1 is in predicate CSG is true for CON.

∀ с 1 ∃ CON (( С 1 ∈ CSC )→ CON ( CSC ))     (6)

[ C1 belongs to CSG with specified Condition and that returns the restricted CSG.]It’s mean that for all tuplesC1 there exists predicate CON is true for C1is exists in CSG implies predicate

CON is true for specified CSG.

Let; Constraints=CON

CON 1= ∀ C 1. ∃ f 1

(( C 1 ∈ CSC ) ∧ fieldname ( f 1) ∧ CON ( C 1. f 1))  (7)

[The dot operator extracts ESG or CSG from the CSG using some specified constraints CON over one or more ESG or CSG defined in schema.]CON1 contains all tuples of C1 extracts the exists predicate such that C1 is exits CSG and filename (f1) and CON (C1.f1) is true.

CON2=∀C2.∃f2((C2∈CSC)∧ fieldname (f2)∧CON (C2. f2))        (8)

CON2 contains all tuples of C2 extracts the exists predicate such that C2 is exits CSG and filename (f2) and CON (C2.f2) is true.

E.g:{ P . Pname | Project

( P ∧ ( ∃ M )( Member ( M ) ∧ ( M . Mid = ”M 07 ” ))}  (9)

• •    Union, Intersection (ᴗ,ᴖ)operators:

These operators will have usual meaning. The union of any two sets A and B , denoted by A ∪ B, is the set of all elements which belong to A or B or both. Hence, A ∪ B = { x : ∈ A OR x ∈ В }.

∀ C 1. ∀ C 2((( C 1 ∈ CSG ) ∨ ( C 2 ∈ CSG )) ∨ CON ( C 1, C 2))→

( C 1 ∪ C 2)                   (10)

• [ C1 or C2 or specify constraints of dot product of C1 and C2 that returns CSG or ESG which belongs to C1 or C2 or both.] For all C1 and C2, C1 is in exist CSG or C2 is in exist CSG or CON over both CSG implies the C1 union C2.

Intersection denoted by A ∩ B, is the set of elements which belong to A and B both and can be expressed as

A∩B= { x: x ∈ A AND x ∈ B } .

∀ C 1. ∀ C 2((( C 1 ∈ CSG ) ⋀ ( C 2 ∈ CSG )) ∧ CON ( C 1, C 2))→

( C 1∩ C 2) )                  (11)

• [ C1 or C2 or specified constraints of dot product of C1 and C2 that returns CSG or ESG which belongs to C1 and C2 .]

For all C1 and C2, C1 is in exist CSG and C2 is in exist CSG and CON over both CSG implies the C1 union C2.

• • Join (|X|) operator:

The join operator is a special case of Cartesian product operator. It is a binary operator to relate two CSGs where one identical ESG must be common. Let, two CSGs are CSG1 and CSG2 . Also let, a set of ESG E1=(E 11 , E 12 ,..., E 1R ) and a set of ESG E2=( E 21 , E 22 ,..., E 2s ) is related with the CSG1 and CSG2 respectively. The join operator between CSG1 and CSG2 is possible iff E1ɅE2≠ ∅ . Now let E1ɅE2= {E a , Eb, E c } then,

{ C 1| C 1 Є CSG 1 Ʌ ƎC 2 ( C 2 ( C 2 ЄCSG 2 ɅC 2. Ea = 1. Ea )}

[SpecifiedCSG in C1 with Existential CSG in C2 and both will satisfy a common ESG field.]

∀ C 1 ∃ c 2 ∃ Ea

((( c 1 ∈ CSG 1) ∧ ( C 2 ∈ CSG 2))→( C 2. E_a = 1. E_a ))

[All CSG in C1 and CSG in C2 and a common ESG field is satisfied then this will return the all common ESG.]

• V. Illustration of Transactional Calculus of Semi-Structured (Tcss) Database by CAP Theorem and Base Theorem

In this section, CAP theorem is as described in propose Semi-structured calculus system is as follows:

In a web concern to transmission collapse, it is difficult for any web service to execute an atomic read/write shared memory that promises a response to every request.

Proof Sketch : Having stated the CAP theorem, it is relatively straightforward to prove it correct. Consider an execution in which the nodes (servers) are partitioned into 2 disjoint set :{ N1} and (N 2 ...N n }. Some node (client) sends a read request to server node N 2. Since N 1 is in a divergent component of the partition from N 2 , every message from N 1 to N 2 is lost. Thus it is intolerable for N 2 to differentiate the following 2 expressions:

• i.    There has been a preceding write of path value p1 requested of node N₁, and N₁has sent an ok response.

• ii.    There has been a preceding write of path value p2 requested of node N₁, and N₁has sent an ok response.

No matter how long N2 waits, it cannot differentiate these 2 cases, and as a consequence it cannot ascertain whether to return response p1 or p2. Server node N2 eventually must return a response, even if the system is segregated; if the message delay from N1 to N2 is sufficiently large that N2 believes the system to be differentiated, then it may return an erroneous response, despite the scarcity of partitions.

The paramount explanation for extending the CAP theorem is to make the point that in the majority of instances, a distributed system can only guarantee two of the features, not all three. To ignore such a decision could have catastrophic results that include the possibility of all three elements falling apart simultaneously.

Consistency: A read sees all previously completed writes i.e. all nodes see the same data at the same time .g: As the above figure I show that, if Project is set as Root then the Path from Project to department can be established and expressed as ; Project (Root)→Member→Department. Let; the path denoted as ρ.

Then, it can be expressed as-

ρ(R,C)= the path from Root to CSG.

Root denoted as R, C(CSG) and E is a trinary relation of (CSG,P,ϴ)

∴∀ i : ( i )[ p is t ℎ e layer ]

And ∀ i : ∃ C : ( opp ( i , C )= Root ) T ℎ en , ∀ i ∶      ( C )→

[ opp ( i , C )]                        (14)

∀ i :[ opp ( i , C )↔ opp ( i -1, c -1)] → Tail ( C ) . (15)

∴  1( R , C ) ∨ p 2( R , C )........ ∨ pn ( R , C )→ p ( R , C ).

For all i , ρ satisfies the layer, for all i and existential C if operator ρ with layer and CSG is satisfied Root then Root implies the operator ρ with layer and CSG. If the operator ρ with layer and CSG satisfies the preceding layer and CSG then it implies the tail node.

Therefore, all nodes see the same data at the same time. In addition, it also satisfy the Base Theorem Basic Availability that means it response to any request.

Availability: Guarantee that every request receives a response about whether it succeeded or failed i.e. read and write always succeed. This means that in GOOSSDM schema there should be a searching path and its return some value. The path value should not be null. Here defining a path means it guarantees that every request receives a response about whether it succeeded or failed i.e. read and write always succeed. When it succeeded then it is succeeded path otherwise, it is failed path.

Succeeded path =N1

Failed Path or(Succeededpath) = N1

∴∀ i : ( i ) [ p is t ℎ e layer ]

And∀i:∃C: (opp (i,C)=Root)(17)

C(CSG)[Let;N1:=opp (i,C)](18)

∃C: Root(C) →N1.(19)

(Succeededpath(N1)) → [ ∃ N 1: N 1( ф ) → Pat ℎ( N 1)]

∃ N 1: (( N 1(ф) → Pat ℎ( N 1)) A ( N 1(ф)

→ Pat ℎ( N 1)Λ( N 1 = (ф)))

For existential C, let succeeded path is not root. Succeeded path implies for existential N1 if N1 value is null then this will be the path value, should not be null, then again for existential N1 returns failed path or succeeded path or succeeded path with not null value.

Therefore, all searching path must return some value. Again, it is also satisfying the Base Theorem Soft State that according to the users’ requirement the desired path will change and it must return some value.

Partition Tolerance:   Guaranteed properties are maintained even when network failures prevent some machines from communicating with others. The system continues to operate despite arbitrary partitioning due to network failures.

Patℎ(Root ,E) [ E is a trinary relation of (CSG,P,e)] ∀i∶      (C)→[opp (i,C)]

∀i:[opp (i,C)↔opp (i-1,c-1)] →Tail(C)(23)

Pat ℎ1( Root , E ) VPat ℎ2( Root , E ) V ... Pat ℎ n ( Root , E )→

Patℎ(Root,E).(24)

For all i, the Root implies operator ρ with layer and CSG. If the operator ρ with layer and CSG satisfies the preceding layer and CSG then it implies the tail node. The all-possible paths of OR operation implies the desired node.

Therefore, the every Node will cultivate q to everywhere it should sooner or later, but the path will continue to receive input and is not checking the consistency of every transaction before it moves onto the next node.

Read-Write Operation Algorithm

Assuming node R is the Root node. The algorithm behaves as follows and A is desired node.

Algorithm 1: Read at node A

Step 1: A sends a request to R for the recent value.

Step 2: If A receives a response from R that means find a path value, then save the value and send it to \\\the client.

By applying algorithm R is the root node and scanning from R to the desired node, A returns the path value with arguments in operator layer no and CSG and it is the finding of path value.

Algorithm 2: Write at node A

Step 1: A sends a message to R with the new path value.

Step 2: If A receives an ACK from R, then A sends an ACK to the client and stop.

Step 3: If A has not yet received an ACK from R, then A sends a message to R with the new value.

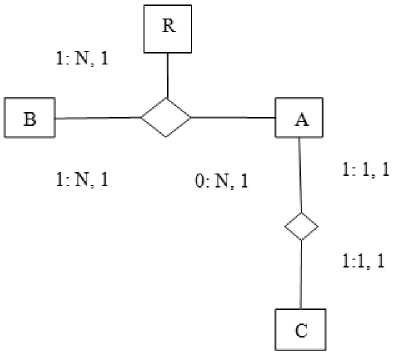
Fig.5. Example of read at node A

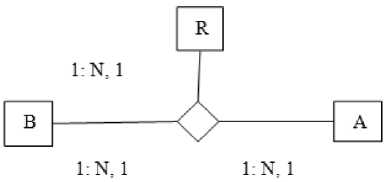
Fig.6. Example of write at node A

A sends request to R for the new path value and R scans it from right to left, i.e. R→B→A; A have to wait to get the ACK and B will get the ACK prior to A and then A sends a message to R with the new value.

Algorithm 3: New value is receiving at node R

Step 1: R increments its sequence no by 1.

Step 2: R sends out the new value and sequence no to every node.

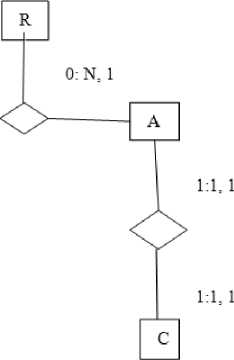
Fig.7. Example of New value is received at node R.

According to previous algorithm Root will increment its layer value by 1 and every node will getting there layer no i.e. sequence no.

• V I. Validation of Transactional Calculus of Semi-structured (TCSS) database by CAP and Base Theorem

Data validation intended to provide certain well-defined guarantees for fitness, accuracy, and consistency for any of various kinds of user input into an application or automated system. Data validation rules can be defined and designed using any of various methodologies, and be deployed in any of various contexts.

Data validation, as explained above, is making sure that all data (whether user input variables, read from file or read from a database) are valid for their intended data types and stay valid throughout the application that is driving this data. What this means is data validation, in order to be as successful as it can be, must implemented at all parts that get the data, processes it and saves or prints the results.

Validation

In evaluating the basics of data validation, generalizations can made regarding the different types of validation, according to the scope, complexity, and purpose of the various validation operations to be carried out. For example:

Data type validation: Data type validation customarily carried out on one or more simple data fields. The simplest kind of data type validation verifies that the individual characters provided through user input are consistent with the expected characters of one or more known primitive data types; as defined in a programming language or data storage and retrieval mechanism. As the above figure I show that, if Project are set as Root then the Path from Project to Department can be established and        expressed        as        ;         Project

(Root)→Member→Department.

Let; the path denoted as p.

Then , it can be expressed as- p(R,C)=i.e. the path from Root to CSG.

• -    Y i: p (i) [p is t^ e I aye r]

And Y i: 3C : ( op p( i, C) = R о о t)          (25)

Then, Yi : R о о t(C) ^ [op p( i, C)]          (26)

Yi: [op p(i, C) ^ op p(i - 1, c - 1)] ^ TaiZ(C).

• -    ( v a I i d.(p a- 1^) ^

This is the simple example of data validation that verifies that the individual characters provided through user input are consistent with the expected characters of one or more known primitive data types; as defined in a programming language or data storage and retrieval mechanism and in previous section it is already proved that it satisfy the CAP and BASE Theorem.

Constraint validation: Constraint validation may examine user input for consistency with a minimum/maximum range, or consistency with a test for evaluating a sequence of characters,

Consistency: A read sees all previously completed writes i.e. all nodes see the same data at the same time.

E .g: As the above figure I show that, if Project are set as Root then the Path from Project to department can be established and expressed as ; Project (Root)→Member→Department.

Let ; the path denoted as ρ.

Then , it can be expressed as-

ρ(R,C)= i.e. the path from Root to CSG.

Root denoted as R, C(CSG) and E trinary relation of (CSG,P,ϴ)

∴∀ i : ρ(i) [p is the layer]

And ∀ I : Ǝc : ( op p ( i , C )= Root )        (29)

Then, ∀ i ∶      ( C )→[ op p ( i , C )]        (30)

∀ i :[ opp ( i , C )↔ opp ( i -1, c -1)] → Tail ( C ).

∴ 1( R , C ) Vp 2( R , C ) ........ ( R , C )→ p ( R , c ). (32)

Therefore, all nodes see the same data at the same time.

This is the simple example of constraint validation and in constraint validation examine for consistency. In previous section it is already proved that consistency satisfy the CAP and BASE Theorem.

Structured validation: Structured validation allows for the combination of any of various basic data-type validation steps, along with more complex processing. Such complex processing may include the testing of conditional constraints for an entire complex data object or set of process operations within a system.

Path(Root ,E)  [ C(CSG) and E trinary relation of(CSG,P,ϴ)]

∀ i ∶      ( C )→[ op p ( i , C )]           (33)

∀ i :[ op p ( i , C )↔ op p ( i -1, c -1)] → Tail ( C ) (34)

Pat ℎ1( Root , E ) VPat ℎ2( Root , E ) V …   ℎ n ( Root , E )

→ Pat ℎ( Root , E ).            (35)

Therefore, the every Node will propagate to everywhere it should sooner or later, but the path will continue to receive input.

This is the example of Structured validation it include complex processing such complex processing may include the testing of conditional constraints for an entire complex data object or set of process operations within a system.

• VII.    TCSS Operators with Example

In previous work defining the GQL-SS algebra for GOOSSDM model that operate on semi-structured schema concept and / or several constructs described in the model. The algebra consists of a set of operators and few of them also can be used with the constructs like ESG, CSG separately. The running example of Project Management System (PMS) used to illustrate the functionalities of operators. As specified earlier path operator (ρ) is also inclusive part of the algebra and invoked every time it is required to invoke any other operator specifically defined for management of semistructured data.

Let consider an example of Project Management System (PMS) where a project has several members and members are associated with some departments. Individual members either may or may not have publications. Moreover, each member may participate in any number of projects. The database for PMS is purely semi-structured in nature. The sample data has been showing in table I.

• A.    Operators in GOOSSDM

Let us note that in GOOSSDM the data are seen as single rooted graphs or multi rooted graph. In every cases have to set an immediate root for the desired CSG and then also find the tail node in respect to the desired CSG.

• •    Select (σ) Operator: The select operator will select CSG and returns CSG that satisfy a given list of ESGs or CSGs from the GOOSSDM schema. The tuple relational calculus (TRC) notation is,

{C|C ∈ CSG }(36)

{C|List(C)}(37)

[List(CSG)=OUTPUT CSG where list={list of ESG}]

If the set of all CSG for which the List(C) evaluates true. And the path expression will be like that-

∀і: ∃С: (op ρ(i, C) = Root)(38)

[for all levels, existential CSG set the path and if it does not have any edge then it is set to Root]

Path(Root, C)(39)

∀і ∶ Root(C) → (opρ(i, C) )(40)

∀ і: (op ρ(i, C) ↔ op ρ(і- 1,c- 1)) → desired(C).

[Searching for desired CSG level by level and get ultimate CSG.]

• •    Retrieve (π) Operator: The retrieve operator extracts ESG or CSG from the CSG using some constraints CON over one or more ESG or CSG defined in GOOSSDM schema.

{C|VC1 E CSG(CON)}           (42)

• [ C1 belongs to some CSG with satisfied condition]

∀ C1 ∃ CON((C1 ∈ CSG) → CON(CSG))    (43)

• [ C1 belongs to CSG with specified condition and that returns the restricted CSG.]Let; Constraints=CON

CON1 =

∀ C1. ∃ f1((C1 ∈ CSG) ∧ fieldname(f1) ∧ CON(C1. f1))

[The dot operator extracts ESG or CSG from the CSG using some specified constraints CON over one or more ESG or CSG defined in schema.]

CON2 =

VC2. 3f2((C2 E CSG) Л fieldname(f2) Л CON(C2. f2))

E. g: {P. Pname|Project(P ∧ ( ∃ М)(Member(M) ∧ (M. Mid=”M07”))}         (46)

• •    Union, Intersection and Difference (ᴗ,ᴖ,and -)operators :   These operators will have usual

meaning. The union of any two sets A and B , denoted by A ∪ B, is the set of all elements which belong to A or B or both. Hence, A ∪ B ={ x: x ∈ A OR x ∈ B}.

∀ C1. ∀ C2(((C1 ∈ CSG) ⋀ (C2 ∈ CSG)) ∧ CON(C1, C2))

→ (C1 ∪ C2)               (47)

• [ C1 or C2 or specified constraints of dot product of C1 and C2 that returns CSG or ESG which belongs to C1 or C2 or both.]

Intersection denoted by A ∩ B, is the set of elements, which belong to A, and B both, expressed as

A ∩ B= { x: x ∈ A AND x ∈ B } .

∀ C1. ∀ C2(((C1 ∈ CSG) ⋀ (C2 ∈ CSG)) ∧ CON(C1, C2))

^ (C1 П C2) )               (48)

• [ C1 or C2 or specified constraints of dot product of C1 and C2 that returns CSG or ESG which belongs to C1 and C2.]

• •    Join (|X|) operator: The join operator is a special case of Cartesian Product operator. It is a binary

operator to relate two CSGs where one identical ESG must be common. Let, two CSGs are CSG1 and CSG2 . Also let, a set of ESG E1= (E 11 , E 12 ... E 1R ) and a set of ESG E2= (E21, E 22 ... E 2s ) is related with the CSG1 and CSG2 respectively. The join operator between CSG1 and CSG2 is possible iff E1ɅE2≠ ∅ . Now let E1ɅE2={E a ,E b , E c } then,

{C1|C1Є CSG1 Ʌ Ǝ C2 ( C2 (C2ЄCSG2 Ʌ C2. Ea =C1. Ea)}

[Specified CSG in C1 with Existential CSG in C2 and both will satisfy a common ESG field.]

[All CSG in C1 and CSG in C2 and a common ESG field is satisfied then this will return the all common ESG.]

• B.    Capabilities of the proposed calculus TCSS

In this section, the expressiveness capabilities of the proposed calculus of TCSS demonstrated by applying the tuple relational calculus to suitable example queries.

• a.    Find the project name and project id from the CSG project1.

{P.Pname, P.PID|Project1 (P)}.

Result:

ABC

P1001

XYZ

P1003

DEF

P1004

XYZ

P1005

ABC

P1001

• b.    Find the details of publication whose Member Id MID=”M03” and Publication Id PuID=”P003”.

In this query, the Retrieve operator has been used with the constraints of select operation on select list as MID =”M03” from Member CSG and also select the list as PID=”P003” from Publication CSG. The calculus can be expressed as follows,

{P.Publication|Project1(p)Ʌ(Ǝ)(Member(M)ɅM.MID=’ M03’)Ʌ(Ǝ)(Publication(B)ɅB.PuID=’P003’)}

Result:

P003

SSS

• c.    Find the details of member where MName=”Bipin” from project1 and also find the details of Member where MName=”Priya” from Project2.

In this query, the Retrieve operator has been used with the constraints of select operation on the list Mname =”Bipin” and Mname =”Priya” from Member CSG. The calculus can be expressed as follows,

{P.Member|Project1(P)Ʌ(Ǝ)(Member(M)ɅM.MName=’ Bipin’)}V{P.Member|Project2(P)Ʌ(Ǝ)(Member(M)ɅM. MName=’Priya’}

Result:

M01

Bipin

XX

M07

Priya

CC

• d.    Find the name of all members who have the same department id “DID=D03” and department name “EE”.

In this query, the Retrieve operator has been used with the constraints of select operation as the list DID=”D03” from Department CSG. Also another Retrieve operator has been used with constraints on select operation as the list DName=”Electrical” from Department CSG. Finally the intersection operator has been used. The calculus can be expressed as follows

{P.Member|Project1(P)A (V □ ) (Member(M))A(H)(Depart ment(D)ɅD.DID=’D03’ɅD.Dname=’EE’} Result:

Rashi

Sashi

• e.  Find the name of the all members who have the

department id same.

In this query, required to set the custom root and then required to apply the join operator. For the purpose, theMemberCSG needs to set the root. The calculus can be expressed by semantics and corresponding result are as follows

Result:

Bipin

Rashi

Sashi

Priya

• f.    Find the project name and project id from the CSG project1 and CSG project2.

{P.Pname,P.PID|Project1(P)}.V{P.Pname,P.PID|Project2 (P)}.

Result:

ABC

P1001

XYZ

P1003

DEF

P1004

XYZ

P1005

ABC

P1001

ABC

P1001

• g.      Find the details of publications where

MName=”Bipin” from project1 and also find the details of publication where MName=”Priya” from Project2.

In this query, the Retrieve operator has been used with the constraints of select operation on the list Mname =”Bipin” and Mname =”Priya” from Member CSG. The calculus can be expressed as follows

{P.Publication|Project1(P)Ʌ(Ǝ)(Member(M)ɅM.MName =’Bipin’)}V{P.Publication|Project2(P)Ʌ(Ǝ)(Member(M) ɅM.MName=’Priya’}

Result:

P001

RRR

P007

NNN

• VIII.    An Implementation of proposed TCSS

A. Transaction Execution:

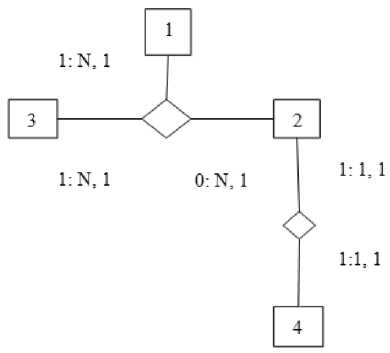
Fig.8. Example of transaction execution

The above figure 8 shows the root node is 1 and then scanning from right, the next node is 2 and the next after next node is 4 after that it scans for the left node 3.Focusing on a simplified variant of TCSS, that is dynamically typed. To introduce the syntaxes and semantics of TCSS, let us starting with a simple example of transactional query by using x-query. In this section, the expressiveness capabilities of the proposed transactional calculus of TCSS demonstrated by applying the calculus to suitable example queries.

ABC

P1001

AAAA

M01

BIPIN

xx

D01

CSE

P001

RRR

XYZ

P1003

CCCC

M03

ASHU

PP

D02

CA

P003

SSS

DEF

P1004

DDDD

M04

RASHI YY

D03 EE

P004 TTT

XYZ P1005

QQQQ

M06

SASHI RR D03 EE

P005 VVV

ABC P1001

BBBB

M07

PRIYA M07

PRIYA CC

D01 CSE

P006 MMM

PQR P1006

YYYY

M07

PRIYA cc

D02CA -

P007 NNN

• 1.    Find the project name and project id from the CSG project1.

where $p1//topics != $p2//topics return

{data($p1//pname)}

{data($p1//pid)}

2. ABC XYZ DEF XYZ ABC P1001 P1003 P1004 P1005 P1001 Find the details of publication whose Member Id
3.	MID=”M03” and Publication Id PID=”P003”. for $p in doc("demo1.xml")//member where $p//mid = "M03" and $p//puid = "P003" return $p//publication P003 SSS Find the details of member where MName=”Bipin” from
4.	project1  and also find the details of Member where MName=”Priya” from Project2. for $p1 in doc("demo.xml")/project/project1/member for $p2 in doc("demo.xml")/project/project2/member where $p1//mname = "BIPIN" and $p2//mname = "PRIYA" return {$p1//(mid,mname,maddress)} {$p2//(mid,mname,maddress)} < table ID= ”project”> M01 BIPIN XX M07 PRIYA CC

Find the name of all members who have the same department

5.

id “DID=D03” and department name “EE”.

for $p in doc("demo1.xml")//member

where $p//dname = "EE"

and $p//did = "D03"

return

{$p//(mid,mname,maddress)}

RASHI

SASHI

Find the name of the all members who have the

6.

department id same

for $p1 in doc("demo1.xml")/project/project1/member for $p2 in doc("demo1.xml")/project/project1/member where $p1//did = $p2//did

and $p1//puid != $p2//puid

return

{data($p1//mname)}

BI PIN

RASHI

SASHI

PRIYA

Find the project name and project id from the CSG

Project1 and Project2

for $p1 in doc("demo1.xml")//project1

for $p2 in doc("demo1.xml")//project

where $p1//topics != $p2//topics
7.	return {data($p1//pname)} {data($p1//pid)} {data($p2//pname)} {data($p2//pid)} < table ID=”project”> ABC XYZ DEF XYZ ABC P1001 P1003 P1004 P1005 P1001 PQR P1006

Find the details of publications where MName=”Bipin”

from project1 and also find the details of publication where MName=”Priya” from Project2.

for $p1 in doc("demo1.xml")/project/project1/member

for $p2 in doc("demo1.xml")/project/project2/member

where $p1//mname = "BIPIN"

and $p2//mname = "PRIYA"

return

{$p1//(puid,ptopics)}

{$p2//(puid,ptopics)}

P001

RRR

P007

NNN

• B.    Implementation of TCSS X-Query

To examine the scalability of proposed TCSS X-Query implementation, trying to perform an experimental evaluation using “Project” xml data. Here also trying to perform a comparison of TCSS X-Query with open source xml processors: BASE-X.

Queries

Here considering 5 basic types of queries: Selection, Retrieve, Union, Intersection and Join.

Selection: Query 1 finds the project name and project id from the CSG project1

{data($p1//pname)}

{data($p1//pid)}

Query 1

Retrieve: Query 2 finds the details of publication whose Member Id MID=”M03” and Publication Id PID=”P003”.

Query 2

Union: Query 3 finds the details of member where MName=”Bipin” from project1 and also find the details of Member where MName=”Priya” from Project2.

and $p2//mname = "PRIYA" return

{$p1//(mid,mname,maddress)}

{$p2//(mid,mname,maddress)}

Query 3

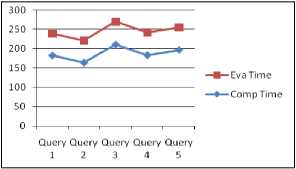
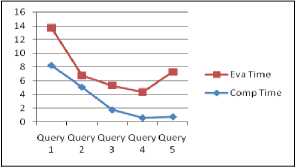
Fig.9. above TCSS X-Query and below BASE-X X-Query

Intersection: Query 4 finds the name of all members who have the same department id “DID=D03” and department name=“EE”.

and $p//did = "D03"

return

{$p//(mid,mname,maddress)}

Query 4

Join: Query 5finds the name of the all members who have the department id same.

{data($p1//mname)}

Query 5

• C.    Experimental Results

This paper performance study explores TCSS X-Query ability. Here in Fig 9 it shows that in case of TCSS XQuery each query execution time is near about same to each other and its maintain a parity, whereas BASE-X xquery processor takes more time for selection procedure and takes less time for join queries. Whereas TCSS xquery time remains comparable, i.e. the additional data is processing in the same amount of time. Here TCSS XQuery demonstrated using a real 10 KB XML dataset (trying to perform an experimental evaluation using “Project” xml data.’) for various XML selection, retrieve, union, and intersection and join queries. In future, planning to analysing of big xml data and optimization of the query compiler.

• VIII. Conclusion

The proposed framework blends semantic of transactional calculus specification and abstraction mechanism with syntaxes in specific modelling. Thus, the paper fulfils the deficiency of systematic methodology in transactional calculus of GOOSSDM model. In addition to this paper proposes a formal transactional calculus called Transactional Calculus for Semi-structured database (TCSS) Further, the transactional calculus is derived from a algebra based query language [11] and illustrated using examples of real life. The benefits of the proposed work are manifold. It provides supports towards (1) representation of precise knowledge of domain independent conceptualisation from structural and functional design concerns with enriched semantics and syntaxes for transactional calculus of semi-structured. (2) realisation of proposed TCSS working with CAP and BASE theorem. (3) a systematic methodology that pave the way of transforming domain analysis. (4) providing guidelines for the purpose of mapping of Transactional Calculus for Semi-structured database. (5) the proposed Transactional system for semi-structured is based on path expression. (6) the path operator is used to set the root node in GOOSSDM schema and also useful to find the path from the root node to desired node for any transaction. (7) facilitate the early verification of the semi-structured data schema structure in correspondence with the desired transactional calculus. The perspective is an extension to this calculus allowing to support larger class of complex queries like aggregates, group by operations.