An Approach to Improve Fisher-Yates Shuffling Based Image Encryption Using Parallelization on CPU

The surge in social media usage has made it integral to people's lives globally, with billions of users engaging on platforms like Facebook, WhatsApp, and Instagram [1]. While these platforms facilitate content exchange, they also pose significant data security and privacy risks, leading to numerous data theft and security breaches. Data, especially personal preferences and information, is crucial in the online world, used by companies to cater to user needs. Among the content shared on social media, images and videos are particularly vulnerable to breaches. To address this, encryption has become a widely accepted method to enhance privacy and security. Platforms like WhatsApp and Signal have implemented encryption effectively, preventing unauthorized access to information [2].

The classification of encryption algorithms has evolved into two categories: Symmetric Key and Asymmetric Key. Symmetric Key algorithms [3-5] use the same key for encryption and decryption, while Asymmetric Key algorithms [6,7] employ separate keys. Symmetric Key approaches include block ciphers, stream ciphers, and hash functions, with well-known examples such as DES and AES [8-10] for block ciphers, RC4 [11] for stream ciphers, and MD-x and SHA-x [12-15] for hash functions. In contrast, Asymmetric Key algorithms, such as RSA [16], use a publicly available key for encryption and a private key for decryption.

Robust encryption is crucial for maintaining security and privacy during data transfer. However, quick encryption and decryption are necessary for real-time applications like social networking. Thus, in order to tackle these two concerns, we suggest a robust and effective approach. The contribution of this study mainly reflects in trifold,

• •    Firstly, a modified FYS-based image encryption algorithm is proposed that uses Fisher-Yates shuffling and SHA256 hashing [24] to ensure confidential transmission of data between sender and receiver.

• •    Secondly, within this algorithm, a parallelization technique is introduced that improves the overall performance. This is achieved by dividing the key generation process into multiple threads, which are executed simultaneously on the CPU.

• •    Thirdly, rigorous testing is performed on a broad spectrum of images with different dimensions, ranging from 128x128 pixels to 4096x4096 pixels, further substantiating the effectiveness of the improved approach. Comprehensive comparisons of the FYS-based image encryption algorithm against the other image encryption algorithms are carried out to prove the efficacy of the approach.

2.    Literature Review

This paper is structured in a manner that allows for a gradual and comprehensive understanding of the parallel implementation of the encryption algorithm discussed earlier. The paper is composed of six sections that progressively build upon each other. The related literature concerning parallel implementations on CPU can be found in Section 2. Section 3 explains the working of FYS based image encryption algorithm and proposes a methodology for the parallelization of the same. The results of the experiments and a comparison of performance between FYS and the proposed Modified FYS-based image encryption algorithm is presented in Section 4. Finally, the conclusion and potential future work of the paper are discussed in Section 5.

The research of improving the performance of image encryption algorithms through multi-core processing in CPUs has been a topic of interest for many scientists and engineers. In the past, several studies have been conducted that explore various highly efficient techniques and algorithms that leverage parallel processing to achieve faster encryption times.

One such study was conducted by Wang et al. [17], in which they proposed an image encryption algorithm that incorporates parallelism for the diffusion stage of encryption. This was achieved by dividing the image into multiple groups, and then performing diffusion using parallel processing in each group twice, along with additional intermediate steps. The algorithm demonstrated increased efficiency with an increase in the amount of data being processed.

Another study was conducted by Song et al. [18], in which they proposed an image encryption algorithm that leverages multiple processors to encrypt batches of images parallelly. The algorithm considers the images to be encrypted as shared resources and utilizes multiple threads to process the images, thereby avoiding interference between threads. The algorithm provides faster encryption when processing a large amount of image data.

Nagendra et al. [19] proposed the implementation of the Advanced Encryption Algorithm (AES) using parallel processing on multicore systems. They used OpenMP to divide the encryption and decryption workload evenly among two cores, and parallel processing was performed only if the number of blocks to be processed was greater than 1000. The parallel processing of encryption and decryption simultaneously on both cores resulted in a decrease in the execution time of the program.

You et al. [20] proposed a hybrid chaotic map-based image encryption algorithm that uses Open Computing Language (OpenCL) for parallelism. The algorithm consists of a confusion phase, which involves scrambling the pixel positions through permutation, followed by a diffusion phase that involves XOR operations and cyclic shifting. The OpenCL implementation improved the speed of image encryption when performed on both CPU and GPU.

Elrefaey et al. [21] proposed the implementation of GPUs to improve the performance of encryption techniques based on chaotic maps. To improve performance, the proposed implementation modified the substitution algorithm for images, and a mapping table was created to parallelize the baker map used in substitution. The GPU was then utilized to carry out the substitution algorithm, resulting in improved performance.

Li et al. [22] proposed a scheme to improve the efficiency of AES by using Compute Unified Device Architecture (CUDA). The scheme processes blocks of 16 bytes simultaneously on multiple threads and T-boxes are stored in on-chip shared memory to increase memory access speed.

He et al. [23] proposed a scheme for using CUDA in parallel processing for multi-dimensional chaotic encryption. The scheme aimed to reduce the repetitiveness of steps in the encryption process, which consumes time, by using a 2D Arnold cat map and a 3D Liu chaotic system for shuffling the positions of pixels and gray-scale encryption of pixels, respectively. The proposed method is claimed to be useful for real-time applications.

3.    Proposed Work

In this section, we present FYS based image encryption algorithm and proposed parallel modified FYS based image encryption algorithm with its complete workflow and step by step code implementation.

• 3.1.    Fisher Yates Shuffle Based Image Encryption Algorithm

In [24], we introduced a new image encryption algorithm that uses a combination of Fisher-Yates shuffling and SHA256 hashing for fast and secure encryption. The algorithm employs a key of arbitrary length to set a time limit for image decryption. The transposition keys for both columns and rows are created and shuffled using a modified version of Fisher-Yates shuffling, providing added security. The number of rounds for transposition depends on the image dimension and each round uses a SHA256 hashed key, resulting in a large and dynamic key space. The study demonstrated the implementation of the algorithm on Android mobile devices through an image viewing library, which allows the sender to encrypt and transmit the image directly to the recipient. The encrypted image can only be decrypted on the recipient’s device and the library prevents unauthorized dissemination and preservation of the image. Attempts to share the image will result in the sharing of the encrypted image. Summarized steps of FYS based image encryption algorithm [25] are as follows:

• •    Step 1: String Key Computation to Generate Initial Seed Key

• •    Step 2: Transposition Key Generation Using Fisher-Yates Algorithm

• •    Step 3: Shuffling of Transposition Key Based Upon Initial Seed Key in Chunk

• •    Step 4: Final Encryption Using Transposition Keys

• 3.2.    Workflow of Proposed Algorithm

• 3.3.    Code Implementation

The FYS-based image encryption algorithm [24] was executed serially and did not make full use of the multi-core architecture that is present on most of the systems today. Specifically, step-3 referred to as ”Shuffling of Transposition Key Based Upon Initial Seed Key in Chunk,” in the above mentioned algorithm, was executed sequentially. However, to enhance its performance, we have implemented parallel processing in this step. In the FYS-based image encryption algorithm, blocks of 16 numbers were taken from the transposition key generated using Fisher-Yates Algorithm to shuffle it further. All the blocks of 16 were processed one after another in serial order. This process was done twice in encryption and twice in decryption and therefore it significantly affects the overall execution time of the algorithm. In this paper, the shuffling process of key generation for column transposition and row transposition is parallelized using multicore architecture and Joblib [25].

A multi-core processor comprises two or more processing units that are individually capable in themselves to execute instructions. This enables the processor to execute instructions simultaneously on multiple cores which in turn helps to reduce the execution time of the program. The cores on a single processor don’t need to be of the same type wherein the cores are called heterogeneous cores. In this case, the cores have a different instruction set architecture (ISA) and are designed for performing specific tasks. If the cores are of the same type they have the same ISA and are called homogeneous cores. Algorithms which aim to utilize multi-core architectures are as important as the hardware itself. The software design plays a key role in determining the improvement in performance with the use of multicore architecture. In some scenarios, where the processing workload is low, dividing the load into multiple cores may lead to a decrease in performance and hence special consideration should be given in deciding whether to use parallel processing or not. For the research proposed in this paper, we have used a quad-core processor with eight logical cores.

Joblib [25] is a library for running Python functions as standalone processes, allowing for the parallel execution of multiple tasks utilizing multiple cores or machines. This can significantly speed up computations, especially for computationally intensive tasks. The Parallel and Delayed functions in the Joblib library are used to initiate parallel threads for processing images. However, the order of execution in the master thread is not ensured, but this does not impact the outcome of the program as long as the statements are independent. The parallel threads are terminated once the workload is processed, and the program continues in the master thread.

The encryption process begins by taking the input image and a string key. The key is appended with the current timestamp and divided by the duration, then hashed using the SHA256 algorithm. Initial transposition keys for row and column are generated using the Fisher-Yates algorithm, and then further shuffled based on an initial seed string equal to that computed in the previous step. The shuffling is done in parallel using the shuffle_key_parallel function, which utilizes the Joblib library and multiple cores to speed up the process. The key is divided into chunks of 64 elements in function, and a seed string is generated for each chunk using the SHA256 hash of the previous chunk’s seed starting with the initial seed string. The shuffle_chunk function is then called, using the chunk’s key and corresponding seed. This function generates a sub-key for every 16 elements of the transposition key. The sub-key is used as an index to swap elements and generate the final transposition key. Here the shuffling process of chunks of length 16 is run in parallel using the Joblib library ((Parallel ( n jobs = -1))) and the number of threads executing in parallel equals the maximum number of logical cores available on the system, which is 8 in this case. Finally, the encryption is performed using the transposition keys generated from the shuffling process. The workflow of the image encryption utilizing multithreading is depicted in Figure 1.

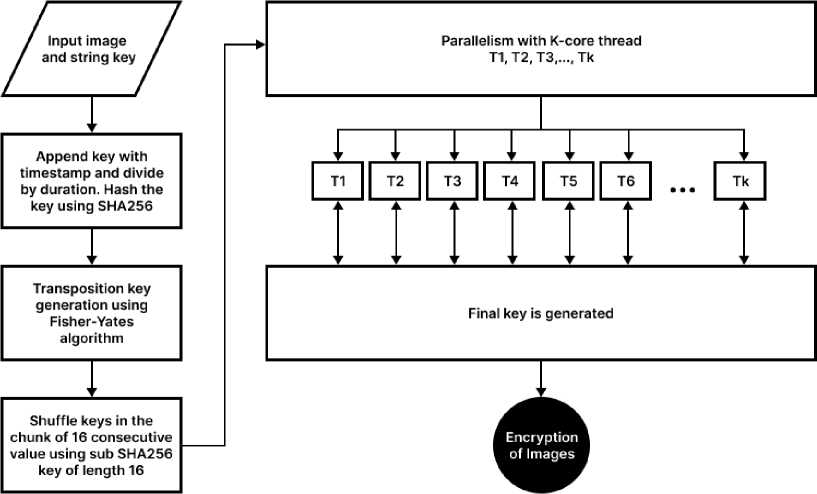
Fig. 1. Workflow diagram of image encryption using multithreading.

In this subsection, step by step code implementation of workflow stated above is described:

Step 2: Transposition Key Generation Using Fisher Yates Algorithm

• #    Fisher Yates Algo

def create_fisher_yates_arr(n):

fisher_yates_arr = []

for i in range(n):

for i in range(n - 1, 0, -1):

j = randint(0, i)

fisher_yates_arr[i], fisher_yates_arr[j] = fisher_yates_arr[j], fisher_yates_arr[i] return fisher_yates_arr

• #    Initialize Array Keys

def initialize_array_key(N, fisher_yates_arr):

arr_key = []

for i in fisher_yates_arr:

if i < N:

return arr_key

Step 3: Parallel Shuffling of Transposition Key Based Upon Initial Seed Key in Chunks def shuffle_chunk(key_chunk , chunk_seed_key , counter , i):

sub_chunk_seed_key = chunk_seed_key[ctr:ctr + 16]

sub_chunk_seed_key = sub_chunk_seed_key + "1A0B95C4D37286EF"

tmp_set = []

tmp_idx = 0

for j in range(i, i + 16):

while sub_chunk_seed_key[tmp_idx] in tmp_set:

tmp_idx += 1

idx = int(sub_chunk_seed_key[tmp_idx], 16)

key_chunk[j], key_chunk[i + idx] = key_chunk[i + idx], key_chunk[j]

def shuffle_key_parallel(key, ln):

seed_key = str_key seed_keys = []

for i in range(0, ln, 64):

Parallel(n_jobs=-1)(delayed(shuffle_chunk)(key, seed_keys[idx // 64], idx % 64, idx) for idx in range(0, ln, 16))

Step 4: Final Encryption Using Transposition Keys def encrypt_image(img, col_key, row_key, N, M):

cols = 0

rows = 0

for i in col_key:

for j in range(0, N):

col_transposed_img[j][cols][0] = img[j][i][0]

col_transposed_img[j][cols][1] = img[j][i][1]

col_transposed_img[j][cols][2] = img[j][i][2]

cols += 1

for i in row_key:

for j in range(0, M):

row_transposed_img[rows][j][0] = col_transposed_img[i][j][0]

row_transposed_img[rows][j][1] = col_transposed_img[i][j][1]

row_transposed_img[rows][j][2] = col_transposed_img[i][j][2]

rows += 1

return row_transposed_img def encrypt_parallel(img):

row_key = initialize_array_key(num_rows , fisher_yates_arr)

column_key = initialize_array_key(num_columns ,fisher_yates_arr)

Parallel(n_jobs=-1)(delayed(shuffle_key_parallel)(key, N)

for key, N in [[row_key, num_rows], [column_key, num_columns]])

final = encrypt_image(img, column_key, row_key, num_rows, num_columns) return final

The decryption process for the encrypted image involves the generation of transposition keys in a manner similar to the encryption process. These keys can then be used to perform the inverse of the encryption process. There is potential to apply parallelism in this step as well to generate the transposition keys more efficiently.

4.    Results and Analysis

In this section, the performance of the proposed algorithm is evaluated on a system with a 2.1 GHz Quad-Core AMD Ryzen 5 processor 3550H, 8 GB RAM, and using Python 3.8. The effectiveness of our proposed algorithm is analyzed using various performance metrics like time of execution and speedup ratio. The extent to which the performance improves by utilizing parallel processing is determined based on the dimensions of the colored input image.

• 4.1.    Runtime comparison on single images of different sizes

  Firstly, this algorithm was executed on single images of different dimensions starting from 128*128 to 4096*4096, which resulted in an average speedup of 1.2 and a maximum speedup of 1.4, as shown in Table 1, below. The graphical representation presented in figure 2 provides insight into the efficiency and performance of the algorithm.

• 4.2.    Runtime comparison on multiple smaller images of same sizes

  Now, this algorithm is further executed parallely on multiple colored images of the same size. To conduct this experiment we have taken images in different numbers starting from 5 up to 1000 and images of various dimensions 128*128 and 256*256. This experiment resulted in an average speedup of 3.5 and a maximum speedup of 5.5 results are attached below in Tables 2 and 3. The graphical representation presented in figures 3 and 4 provides insight into the efficiency and performance of the algorithm when run on many images of the same sizes.

Table 1. Runtime comparison of the serial and parallel implementation of the algorithm on the colored images of different sizes.

Image size	CPU time (in sec.)	CPU time for parallel processing (in sec.)	Speedup
128*128	1.003223658	1.026697636	0.9771364253
256*256	1.283094645	1.281639576	1.001135318
512*512	2.547187328	2.296122789	1.109342819
1024*1024	9.148190498	6.56148386	1.394225863
2048*2048	27.85075712	23.60220742	1.180006455
4096*4096	134.002821	93.86824751	1.427562829

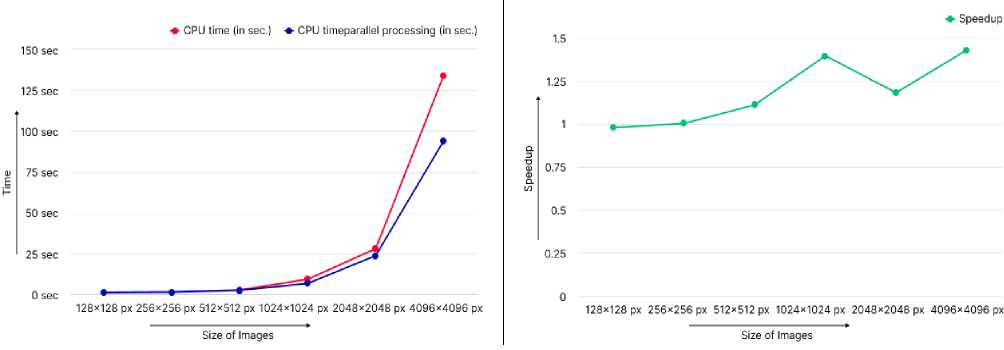
Fig. 2. Overall Speedup and Runtime of the serial and parallel implementation of the algorithm on the images of different sizes.

Table 1 and Figure 2 illustrate the speedup achieved through parallel processing, ranging from approximately 0.9 to 1.4 for smallest and largest image respectively, which is somewhat less significant than anticipated. Interestingly, there is absolutely no noticeable speedup for photos of 128x128 and 256x256 pixels (0.9 and 1 respectively). It follows that in the case of small-sized photos, the overhead is greater than the benefits of parallel processing.

But, we have further analyzed that to use this algorithm efficiently on images of small sizes, it's better to run this algorithm parallely on multiple images at a time.

Table 2. Runtime comparison of the serial and parallel implementation of the algorithm on the multiple colored images of the same size (128x128 px).

Number of Images	CPU time (in sec.)	CPU time for parallel processing (in sec.)	Speedup
5	1.228190899	2.220919847	0.5530100063
10	2.144198656	2.51624918	0.8521408266
15	3.34150219	2.714780569	1.230855351
20	4.340431929	3.172062159	1.368331297
25	5.574463844	3.681206942	1.514303307
30	6.539833307	3.668137789	1.782875585
40	9.115839958	4.356165886	2.092629206
50	11.05693197	5.05211997	2.188572725
70	15.21333218	6.585171461	2.310240859
100	21.85889387	8.431094408	2.592652011
150	32.39831352	10.98157477	2.950242947
300	65.77128768	20.23828053	3.249845636
500	109.6669927	31.58474755	3.472150362
1000	210.4681835	61.94662452	3.397573075

Table 3. Runtime comparison of the serial and parallel implementation of the algorithm on the multiple colored images of the same size (256x256 px).

Number of Images	CPU time (in sec.)	CPU time parallel processing (in sec.)	Speedup
5	5.085122108	2.814784527	1.806575978
10	9.369439602	4.224379539	2.217944556
15	13.95714378	4.316452026	3.233475942
20	18.24821448	5.915573597	3.084775159
25	23.04440761	6.092336178	3.782523967
30	27.23966336	6.85735178	3.972329878
40	36.0323875	7.820211172	4.607597762
50	36.14592099	10.03760624	3.601049905
70	56.70106936	12.48620868	4.541095766
100	86.65430164	15.60832286	5.551800948
150	128.0053725	24.66508937	5.18973885
300	101.7875721	37.08334112	2.74483283
500	308.2408321	67.86592221	4.541908841
1000	342.7452867	119.1329706	2.876997737

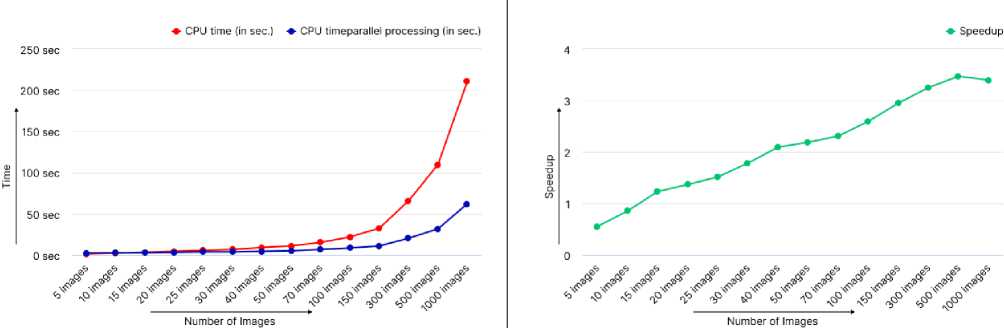
Fig. 3. Overall Speedup and Runtime comparison of the serial and parallel implementation of the algorithm on the multiple images of the same size (128x128 px)

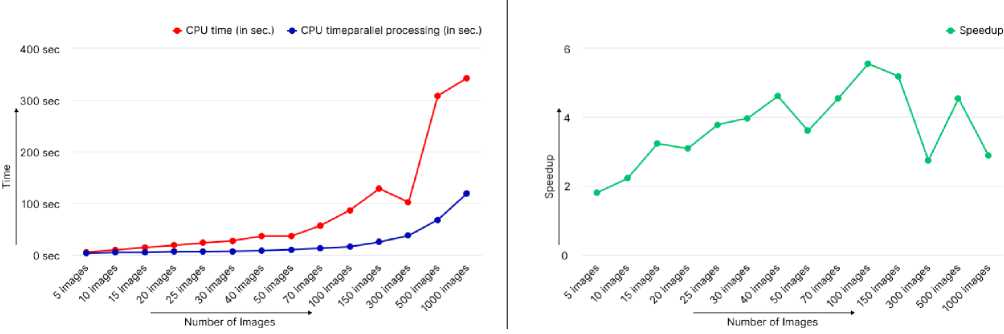
Fig. 4. Overall Speedup and Runtime comparison of the serial and parallel implementation of the algorithm on the multiple images of the same size (256x256 px)

Thus from subsections 4.1 and 4.2, it can be concluded that the optimal performance of the proposed FYS-based image encryption algorithm requires a balance between the level of parallelism utilized and the size of the images being processed (S). Too much parallelism could lead to overheads and decreased performance when working with smaller images (As seen for the smaller images in subsection 4.1), while insufficient parallelism may result in slower processing times for larger images (As parallel approach can provide massive speedups, up to 5.5 times, as seen in subsection 4.2). Hence, it is crucial to find the right balance between the two factors to achieve optimal performance. This balance can be achieved through careful tunings of the algorithm’s parameters, such as the number of parallel processes and the size of the image chunks being processed in parallel. By carefully considering these factors and adjusting the algorithm accordingly, the proposed solution can deliver high-performance encryption for a wide range of image sizes.

• 4.3.    Comparison with other approaches

5.    Conclusion

We have conducted a comprehensive comparison of the FYS-based image encryption algorithm against both traditional methods (such as Vigenère Cipher [20], RC4 [11], Salsa20 [26], DES [8-10], 3DES [9], AES [8-10], ECC [26]) and modern approaches (including Chaotic map [26], Hyper-chaotic map [27], 2D-CLSS hyperchaotic map [28]). All approaches were tested on a single 256x256 pixel grayscale image, with the evaluation based on encryption time and security.

While Vigenère Cipher exhibits the fastest encryption time, it fell short in meeting fundamental security standards, rendering it unsuitable for real-world scenarios like social networking. Among the mentioned approaches, the FYS-based image encryption algorithm emerged as the top performer considering both the parameters. Furthermore, parallel encryption enhancements contributed to further improving the algorithm's performance.

Table 4 provides a summary of the encryption analysis for these algorithms, underscoring the effectiveness of our proposed approach. Apart from the grayscale images, the proposed approach performs exceptionally, well for a large number of colored images as witnessed in previous subsections.

Table 4. Comparison of the FYS-based encryption algorithm with other approaches based upon encryption time as well as security of each encryption method on a 256x256 grayscale image

Techniques	Encryption Time (in seconds)	Security
Vigenère [20]	0.01634	Bad
RC4 [11]	0.23275	Good
Salsa20 [26]	1.3875	Good
DES [10]	49.1286	Good
3DES [9]	143.7368	Good
AES [10]	169.4769	Good
ECC [26]	202.1892	Good
Chaotic map [27]	0.37168	Great
Hyper-chaotic map [28]	0.45343	Great
2D-CLSS hyperchaotic map [29]	0.459837	Great
FYS-based image encryption [24]	0.2325583333	Great
FYS-Based image encryption with Parallelism	0.2322946051	Great

As the number of data transfer and computing devices grows, there is a greater need for data encryption that is both quick and secure. This paper firstly presented an image encryption algorithm based on the FYS method, which incorporated a timeout feature for enhanced security and privacy, regardless of the key size. As this implementation was sequential and did not fully utilize the multi-core architecture available in modern computer systems. As a result, a more efficient implementation for FYS-based image encryption by parallelizing the algorithm on a CPU was proposed, which improved its speed without losing its security and privacy aspects.

Our new solution achieves parallelization of the key generation process through column and row transposition, taking advantage of the multicore architecture and the Joblib library. This allows for multiple key generation processes to be executed simultaneously on different cores, leading to a significant improvement in the speed of the encryption process. This resulted in an average speedup of 1.2 and a maximum speedup of 1.4 when executed on single images of different sizes, compared to the FYS-based image encryption algorithm. However, when processing small-sized images, the overhead may outweigh the benefits of parallel processing. In such cases, it is more efficient to run the algorithm in parallel on multiple small-sized images, resulting in an average speedup of 3.5 and a maximum speedup of 5.5 times when executed in parallel on multiple images of the same sizes compared to FYS based image encryption algorithm. Therefore, it can be concluded that the optimal performance of the proposed FYS-based image encrypt           tion algorithm is achieved by finding a balance between the level of parallelism and the size of the images being processed.

In the future, this algorithm has the potential for implementation on a GPU for fast encryption and decryption on devices with inbuilt GPU capabilities, leveraging its graphical processing capabilities.

Acknowledgment

We would like to express our gratitude to the reviewers for their precise and succinct recommendations that improved the presentation of the results obtained.

Funding

The authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Research Data Policy and Code Availability

The data generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Human and animal rights

This article does not contain any studies with human participants or animals performed by any of the authors.

Conflict of Interest

The authors have no conflict of interest to declare that are relevant to the content of this article.