An approach to parallel sorting using ternary search

Published Online April 2018 in MECS DOI: 10.5815/ijmecs.2018.04.05

People wants improvements in productivity, security, multitasking (running multiple application simultaneously on your computer), data protection, and many other capabilities. Performance of a processor can be increased by increasing clock speed ,increasing bus speed and by providing large cache memory. Given the large number of parallel sorting algorithms and wide variety of parallel architecture, it is a difficult task to select the best algorithm for a particular machine and problem instance. The main reason that the choice is more difficult than in sequential machines is because there is no known theoretical model that can be applied to accurately predict an algorithm’s performance on different architectures.

This paper present a new parallel sorting algorithm for multi-core machine in most inexpensive rate. The contribution of this paper are as follows:

• •    We piecemeal the original data based on cores of the hardware , thereby reduce the time of processing.

• •    We divide all of the data into processors averagely to ensure load balance.

• •    Counting Sort is used for sorting every data block.It provide stable sorting.

• •    We merge all processors using ternary search in parallel, then got the global ordered data. Proposed algorithm avoids the expensive unaligned load/store operations.

It is our hope that our results can be extrapolated to help select appropriate candidates for implementation on machines with architecture similar to those that we have studied.

• A .    Multi-Core Processor

A multi-core processor is a single computing component with two or more independent actual processing units, which can read and execute program instructions. Multiple cores are able to execute two or more programs at the same time so improving overall speed to parallel computing. Manufacturers typically integrate the cores onto a single integrated circuit die (chip microprocessor or CMP), or multiple dies in a single chip package.

• B .    Parallel Programming

The software world has been very active part of the evolution of parallel computing. Parallel program are hard to write than the sequential one. A program that is divided into multiple concurrent task is difficult to synchronization and communication that need to take place between those tasks.

The computational problem should be able to

• •    Be broken apart into discrete of work that can be solved simultaneously.

• •    Execute multiple program instructions at any moment in time.

• •    Be solved in less time with multiple compute resources than with single compute resources.

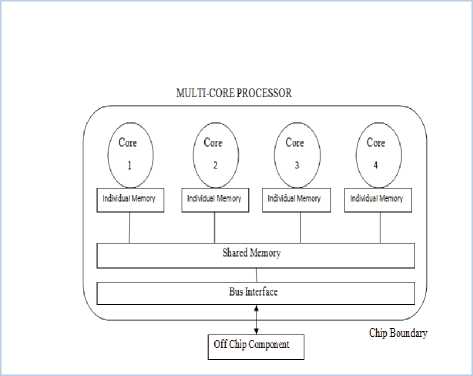
Fig.1. Logical view of multi-core processor

Fig.2. Parallel execution of instructions

The other sections of this paper presented are as follows section 2 describes related work. Section 3 describe the MATLAB. Section 4 describes the proposed algorithm. Section 5 describes the computational complexity of proposed parallel sorting algorithm. Section 6 represents the experimental results of propose algorithm and comparisons with other algorithm. Section 7 concludes the paper with discussion of results and scope for future work.

Parallel sorting Algorithm

• C.    Counting Sort

Counting sort is one of the linear sorting algorithms for integers. It assumes that each of the n input elements is an integer in the range 0 to k, for some integer k. When k=O(n), the sort runs in T(n) time[1].

The basic idea of counting sort is to determine, for each input element x, the number of elements less than x. This information can be used to place elements x directly into its position in the output array. e.g. if there are 17 elements less than x, then x belongs in output position 18.

Counting sort beats lower bound of Ω(n lg n) because it is not a comparison sort. Counting sort uses actual values of elements to index into an array.

EXAMPLE

Unsorted list:

1    2    3    4    5    6    7    8

2

5

3

0

2

3

0

3

0    1    2    3    45

C   2 □ 0 □ 2 □ 3 □ 0 □

0    1    2    3    45

C   2 □ 2 □ 4 □ 7 □ 7 □

1   2   3   4    5   6   78

B iiii m i3Ii

So, After all steps Final sorted list

1   2   3    4   5    6   78

B      0   0   2   2   3   3   35

In practice, we usually use counting sort when we have k=O(n), in which case the running time is T(n).

• D.    Ternary Search

Suppose we are given an array of records that is sorted(ascending order). The implementing ternary search require to split the data sequence into three parts. After that data is compared with two mid points based on the comparison data is searched in particular parts[2].

Example: sorted list

A   2 □ 4 □ 6 □ 8 □ 13 □ 15 □ 19 □ 21 □ 24 □

Mid1=(9/3)=3

Mid2=Mid1*2=6

Now key to search is 6 A(Mid1)==6

In this way searching is done.

Time complexity of algorithm is O(log 3 n) in average and worst case. In best case it is O(1).

So due to the complexity of Ternary Search it gives the better performance than Binary Search an any other Linear Search.

Result shows that proposed algorithm is better than others for large data sequence.

The propose algorithm takes less time than other sorting algorithms.

Table 1. Execution Time Of Binary Search And Ternary Search

Number of input values(n)	Binary Search(time in seconds)	Ternary Search(time in seconds)
10	2.64	1.73
20	2.90	2.02
30	3.03	2.25
40	3.10	2.42
50	3.44	2.90
75	3.69	3.11
100	3.71	3.02
500	3.92	3.20
1000	4.02	3.22
10000	4.84	3.46

The table I shows the execution time for Binary Search and Ternary Search. From the above table it is clear that Binary Search takes more time than the Ternary Search for any size of input. Here Ternary Search takes less time because it gives three attempt to search for a value in single iteration.

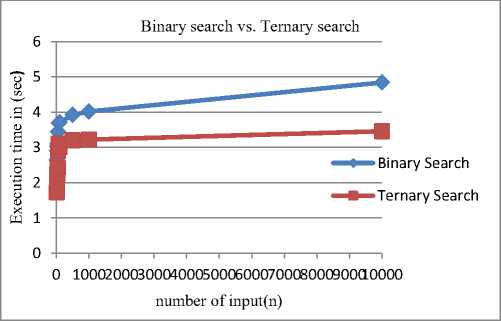
Fig.3. Execution time of binary search and ternary search

• E.    Parallel Merge Sort

First of all split data set in half. Sort each half recursively. Merge them back together to a sorted list. The merge sort algorithm can be parallelized by distributing (n/p) processors to each processor. Each processor sequentially sorts the sublist and then return to final sorted list.

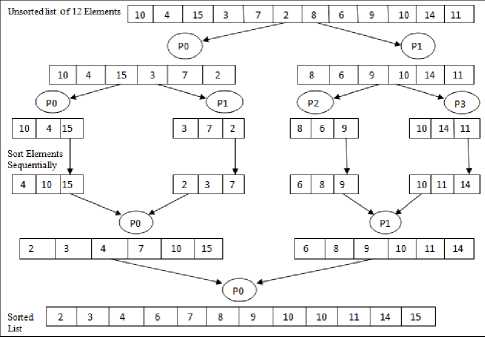
Fig.4. Example of Parallel Merge Sort

Parallel merge sort time complexity:

• 1.    In sequential environment O(nlogn).

• 2.    In parallel environment O((n/p)log(n/p)).

• F .    Odd Even Sort

In this sorting algorithm datasets are distributed into p processors. After this all processors sort data locally. Now in even phase all even numbered processors are communicating with their right neighbour processor whereas in odd phase all odd numbered processors are communicating with next processors.

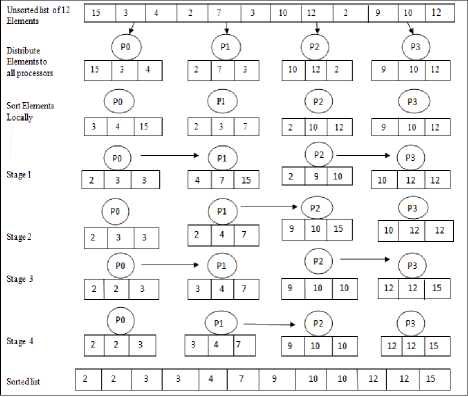
Fig.5. Example of Parallel Odd Even Sort

• G.    Bitonic Sort

In this sort first of all divide the list into two halves. Compare and exchange each item in each item in first half with the second half.

If number of steps(P=n)

In oreder to form a sorted sequence of length n from two sorted sequence of length n/2, there is log(n) comparator stages required.

T(n)=log(n)+T(n/2)

The solution of this recurrence equation is,

T(n)=log(n)+log(n)-1+log(n)=2+….+1=log(n).(log(n)+1)/2

Each stage of sorting network consists of n/2 comparators. On the whole, these are θ(n.log2(n)) comparators.

For P=n,   T(n)=θ(n.log2(n))/n=θ(log2(n))

• II.    Related Work

There has been little work done to parallelize the search algorithms, using different strategies and parallel architectures. Some other parallel sorting algorithm has been in area. Efforts has been put in various algorithms specially sorting algorithms to reduce execution time, speed up , making utilization of cores on its maximum.

Few approaches [14] are given to make the utilization of cores by turning serial to parallel algorithms on different underlying operating system and tools.

In our proposed work we have improve the performance of algorithm making it to work with other algorithms so that time to execution is reduced and all the available cores are utilized.

• III.    Matlab

It allows you to solve computationally data-intensive problems using multi-core processors, MATLAB-PCT and computer clusters. High level constructs- parallel for-loops, special array types and parallelized numerical algorithms lets you parallelize MATLAB applications without CUDA or MPI programming

PCT allows us to convert the applications to take advantage of computer equipped with multicore processors and MATLAB-PCT. Now we can run the same application on a variety of computing resources without reprogramming it. The parallel constructs function in the same way, regardless of the resource on which your application runs- a multicore desktop or on a larger resource.

• A .    Spmd

It executes code in parallel on a worker of parallel pool.

Syntax spmd ,statements, end spmd(n), statements, end spmd(m,n), statements, end

The general form of spmd(single program multiple data) statement is:

spmd statements end

The spmd statement can be used if you have PCT. To execute statements in parallel you must open a pool of MATLAB workers using parpool or having parallel preferences allow automatic start of a pool.

Inside body of spmd statement, each MATLAB worker has a unique value of labindex, while numlabs denotes the total number of workers executing the block in parallel. Within the body of the spmd statement, communication functions for communicating jobs(like labSend, LabReceive) workers.

When there are no MATLAB workers available, MATLAB executes block body locally and creates Composite objects as necessary.

• B.    Example spmd(4)

A= magic(3) end

worker 1 worker 4	worker 2		worker 3
8 1 6 1 6	8 1 6	8 1 6	8
3 5 7 5 7	3 5 7	3 5 7	3
4 9 2 9 2	4 9 2	4 9 2	4

• C .    Codistributed

It creates codistributed array from replicated local data. Syntax

C=codistributed(X)

C=codistributed (X, codist)

C=codistributed(X, lab, codist)

C=codistributed(C1,codist)

C=codistributed(X) distributes a replicated array X using the default codistributor, creating a codistributor array C as a result. X must be a replicated array, that is, it must    have    the    same    value    on    all workers.C=codistributed(X,codist     )distributes     a replicated array, X using the distribution scheme defined by codistributor codist. X must be a replicated array means it must have same value on all workers. Size(C) is same as size(X). C=codistributed(X,lab,codist) distributes a local array X that resides on the worker identified by lab, using the codistributor codist. Local array X must be defined on all workers, but only the value from lab is used to construct C. C= codistributed(C1,codist) accepts an array C1 that is already codistriduted and redistributes it according to the distribution scheme defined by the codistributor codist.

• D .    Example

Creating a 10-by-10 codistributed array using default distribution scheme.

spmd(4)

A=100;

B=magic(A); % Replicating over workers

C=codistributed(B); % Distributing among workers

End

• IV.    Proposed Work

Our proposed parallel sort is a hybrid algorithm, the combination of Counting sort and Ternary search.

First it split the data sequence into several groups then apply counting sort concurrently on all the groups at individual processors. After that it uses ternary search to find the correct position of each element in the global list concurrently. Then copy the elements of the data sequence to corresponding position to obtain the final sorted data sequence.

Let us suppose a shared memory multiprocessor with n processors, represented by P1,P2,…Pn. Let us given another data sequence D of size S which is initially unsorted and one more data sequence of d of size S which is initially empty. The proposed algorithm first of all split the data sequence into n subsequences of size Sn. Each subsequence is denoted by Di and given to processor to Pi where i is ranging from 1 to n.After getting subsequence Di of size Sn to all the n processors every processors Pi start sorting it parallely using counting sort.

Then we use ternary search to find the global index of each element of Di in global sorted list D . For indexing every element of Pi[k] of Di is searched in Do on all processors where o=1 to n.

If this first element Pi[k] is less than first element of Do will contribute in the indexing of Pi[k]. If last element of Do is less than the Pi[k] then all the elements of Do will contribute indexing of Pi[k], otherwise we apply ternary search to find the global index [Mo] of the element Pi[k] in Do. In this way global index of all elements on individual processors are calculated and using this index final sorted list is achieved.

Algorithm:

Data sequence D, Size of the array S, FE: First element of corresponding processor, LE: Last element of corresponding processor.

Start

• 1-    For all processors Pi do parallel.

• 2-    Apply Counting sort on Di. End.

• 3-    For j=1 to n

• 4-  For k=1 to S/n

• 5-  For 0=1 to n

• 6-  If(Pi[k]

  o[FE])

• 7-    break;

• 8-    else (Pi[k]>P 0 [LE) then

• 9-    break;

• 10-    elseif apply Ternary Search to find the number of elements Mo are smaller than Pi[k] in Po.

• 11-    End if.

• 12-    Xi[k]=Xi[k]+Mo

• 13-    Copy the elements of data sequence D to corresponding position in data sequence.

• 14-    Final sorted data sequence is achieved.

End

• A. Example

Unsorted list

• 12, 10, 34,  52,  37,  65,   54,   90,   27,   48,   69,

Step-1 Distribute all elements on corresponding processors.

P0	P1	P2	P3
{12,10,34}	{52,37,65}	{54,90,27}	{48,69,87}
Step-2 Apply Counting Sort at individual processor locally.
P0	P1	P2	P3
{10,12,34}	{37,52,65}	{27,54,90}	{48,69,87}
Step-3 Find out sorted index of element using ternary search.
P0	P1	P2	P3
{1,2,4}	{5,7,9}	{3,8,12}	{6,10,11}

Step-4 Copy elements to index position to get sorted data sequence.

10, 12,  27,  34,  37,  48,  52,  54,  65, 90

69,

87,

In the above example we have taken unsorted list of 12 elements and the system is having 4 processors.

Step-1 In this we have distributed the elements to all processors in equal amount.

Step-2 In this we have sorted the elements using counting sort on each processors. In this all processors will work.

Step-3 In this index of elements are achieved.

For example 10 in P0 will compared with FE of P1.If FE of P1 is greater than 10 than it will not contribute in indexing of 10. If LE of P1 is less than 10 than all elements of P1 will contribute in indexing of 10. If FE of P1 is less than 10 but LE of P1 is greater than 10, in this case we apply ternary search to find the index of 10 in the list.

Step-4 Here we copy the elements to their index position in the final data sequence.

• V.    Computational Complexity

The complexity of algorithm is divided into two parts: First counting sort phase complexity and second ternary search phase complexity.

In our propose algorithm counting sort is use in parallel to sort the each subsequence of size S, so that computational complexity of first phase is O(S/n).Ternary search phase complexity: The second phase is used to find the index of each sorted element using ternary search. The complexity of ternary search for n elements in best case is O(1) and in worst case it is O(log 3 n). In the proposed algorithm ternary search is used to find out the sorted position of an element in subsequences of size Sn and find the position in all S subsequences. So complexity of second phase is O(n* log 3 S/n).

Proposed algorithm complexity: Based on above analysis the computational complexity of proposed parallel sorting algorithm is O(S/n) + O(n log3 S/n).

• VI.    Implementation and Experimental Evaluation

  To implement this algorithm, MATLAB R2010a, we distribute all the elements on respective labs and sort each subsequence through by using sequential counting sort locally. Now we use the result of each lab. On each labs applies ternary search to find the index of each element of data sequence D. After that copy elements to the

We have one an experimental evaluation of our proposed algorithm using MATLAB R2010a. And we are using windows 7 as operating system with RAM 4 GB and Intel(R) core (TM) i3-4005U CPU @ 1.70 GHz as processor.

Here we have computed the execution time of proposed algorithm on MATLAB with existing parallel merge sort algorithm and Binary Search Based Sorting algorithm .We have calculated performance of all algorithms on a large data sequence having number of elements from 1K to 100K.

Table 4. Execution Time For Binary Search Based Sort Vs. Proposed Sort

No of Inputs(n)	Binary Search Based Sort	Proposed Sort
1K	1.27	1.16
10K	10.23	9.61
30K	12.31	11.87
60K	13.16	12.10
90K	15.66	14.06
100K	16.43	15.16

In the table IV the execution time for Binary Search Base Sort and Proposed Sort is shown. For any type of input time taken in binary search based sort is always greater than the proposed sort. So the proposed sort takes less time for the data and gives the performance improvement.

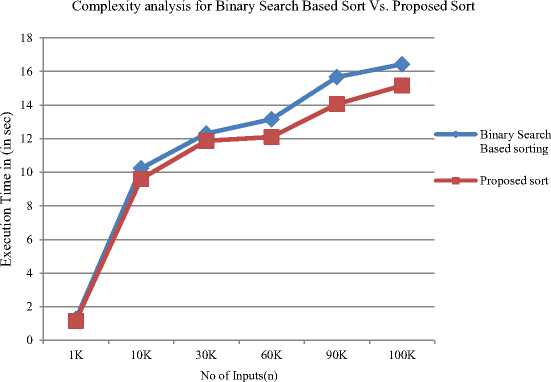
Fig.6. Execution time for binary search based sort vs. proposed sort

Table 5. Execution Time For Parallel Merge Sort Vs. Proposed Sort

No of Inputs(n)	Parallel Merge Sort	Proposed Sort
1K	1.68	1.16
10K	11.87	9.61
30K	13.77	11.87
60K	16.37	12.10
90K	21.76	14.06
100K	23.88	15.16

In the table V we have shown the execution time for Parallel Merge Sort and Propose Sort. After analyzing the execution time for both sorting we can say that for any type of input proposed sort takes less time in all cases. And in this way proposed sort gives better performance.

• A. Performance view on the basis of core utilization

Normally in parallel sorting algorithm all the processors are not used at every instance of time but in our propose algorithm all processor are utilized at all. It gives speed up of almost two times for parallel sort algorithms on a MATLAB-PCT based machine. Time taken in few cases was less than one-fourth. Percentage will increases many times as number of input increases.

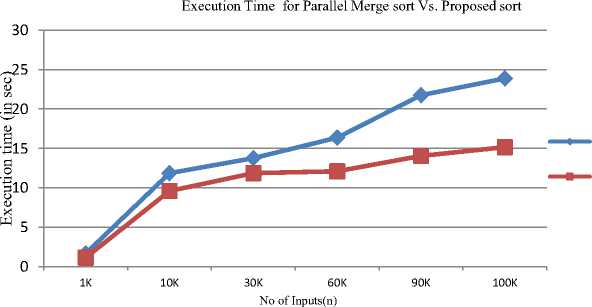
Parallel Merge sort

Proposed sort

Fig.7. Execution time for parallel merge sort vs. proposed sort

Case 1 When no load applied on processors

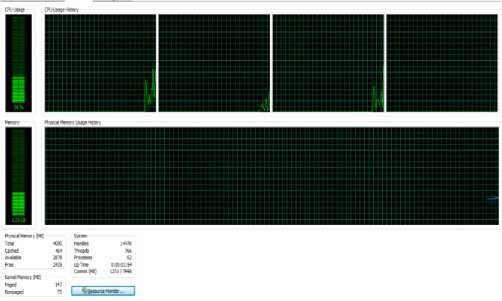
Fig.8. CPU Performance when no load applied

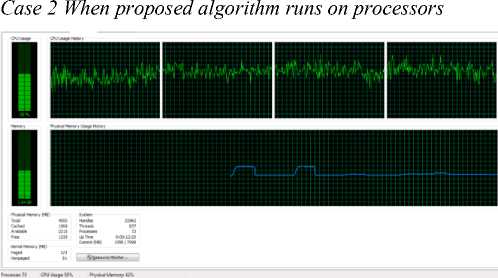
Fig.9. CPU Performance when proposed algorithm runs

• VII. Conclusions

In this dissertation work a new parallel sorting algorithm that we say Ternary Search: An Approach to Parallel Sorting is given. The proposed algorithm takes less time for execution. It gives speed up of almost two times for parallel sort algorithms on a MATLAB-PCT based machine. Normally in parallel sorting algorithm all the processors are not used at every instance of time but in our propose algorithm all processor are utilized at all.

Parallel programming provide great performance improvement. Time taken in few cases was less than onefourth. Percentage will increases many times as number of input increases.