An Efficient and Simple Switching Filter for Removal of High Density Salt-and-Pepper Noise

Published Online October 2013 in MECS (http://www.

Digital images are corrupted by undesirable random variations in intensity values called noise [1]. During image acquisition or transmission, digital images could be contaminated by impulse noise, which is caused by malfunctioning pixels in camera sensors, faulty memory locations in hardware, or transmission in a noisy channel [2]. It’s important to eliminate noise before subsequent image processing tasks such as edge detection or segmentation is carried out. Salt-and-pepper noise is a special case of impulse noise where the noisy pixels can take only the maximum and minimum values in the dynamic range. Recently, many algorithms such as [2-6] have been proposed to carry out the salt-and-pepper noise suppression. Therefore, to efficiently remove noise from an image while preserving its features is a fundamental problem of image processing [7]. The standard median filter (SMF) is the most popular choice for removing the salt-and-pepper noise. However, the median filter and its derivations such as weighted median (WM) [8], center weighted median (CWM) [9], and recursive weighted median (RWM)[10] are typically implemented invariantly across an image. They tend to alter the noise free pixels as well as the noise pixels, exhibits blurring of filtered images. To avoid the damage on the noise free pixels, many image filters with an impulse detector are proposed such as in the literatures [4],[1113].

In this paper, an efficient and simple method to remove salt-and-pepper noise is proposed. In this method, only the noise pixels are changed by filter operation, while the noise free pixels are kept unchanged. In addition, the window size is altered among 3X3 and 5X5 based on the noise and noise free pixels within the window. This technique requires only one original nonnoise image as data set. May be the median value or other values based on the median are not the correct choice for noise pixel replacement. Thus, the filter output is based on the solution of the system X=A-1B in the nonnoise original image which will be explained later. Further, this method does not require threshold parameters. This method can remove salt-and-pepper-noise with a noise level as high as 97%, and it’s relatively fast. The experimental results demonstrate that the proposed method is effective for removing noise and preserving fine details than other existing methods. The outline of this paper is organized as follows. A brief review of related work is given in section II. In section III, the proposed technique is introduced. The implementation results and comparison are provided in section IV. Finally, the conclusions are summed up in section V.

• II.    RELATED WORK

Many approaches have been proposed to remove salt -and- pepper noise. Chang-you et al [13] have proposed an adaptive weighted median filtering algorithm to remove salt -and- pepper noise. This algorithm first takes a decision whether the pixel under test is noise or not by comparing the block uniformity of the 3x3

window with one of the entire image, then adjusts the size of filtering window adaptively according to the number of noise points in the window. Further, Toh and Isa [11] have proposed two-stage noise adaptive fuzzy switching median (NAFSM) filter for salt-and-pepper noise detection and removal. The detection stage will use the histogram of the corrupted image to identify noise pixels. These detected the noise pixels will and then by filtering action, while noise free pixels are retained and left unprocessed. Then, the NAFSM filtering mechanism employs fuzzy reasoning to handle uncertainty present in the extracted local information as introduced by noise. Haidi et al. [14] have proposed a technique to remove impulse noise from highly corrupted images. The method is actually a hybrid of the adaptive median filter with the switching median filter. The method adaptively changes the size of the median filter based on the approximation of local noise density. Haidi et al [14] claimed that their method is better than the works in [15-17]. In addition, K. S. Srinivasan and D. Ebenezer [18] have proposed a decision-based algorithm (DBA) for restoration of images that are highly corrupted by impulse noise. This algorithm shows significantly better image quality than a standard median filter (SMF), adaptive median filters (AMF), a threshold decomposition filter (TDF), cascade, and recursive nonlinear filters. This method processes the corrupted image by first detecting the impulse noise. The detection of noisy and noise-free pixels is decided by checking whether the value of a processed pixel element lies between the maximum and minimum values that occur inside the selected window. This is because the impulse noise pixels can take the maximum and minimum values in the dynamic range (0, 255). If the value of the pixel processed is within the range, then it is an uncorrupted pixel and left unchanged. If the value does not lie within this range, then it is a noisy pixel and is replaced by the median value of the window or by its neighborhood values. Furthermore, Cangju Xing [5] has proposed a method for removing heavy salt-and pepper noise. This method includes three steps. In the first step, the noise pixels are distinguished from the signal pixels; then set initial values for noise pixels; finally, compute the output. The main difference from other switch-type filters is the means to change the values of the contaminated noise pixels. Furthermore, a modified decision based unsymmetrical trimmed median filter algorithm (MDBUTMF) for highly corrupted image by salt -and- pepper noise is proposed in [19]. This algorithm replaces the noisy pixel by trimmed median value when other pixel values, 0’s and 255’s are present in the selected window and when all the pixel values are 0’s and 255’s then the noise pixel is replaced by mean value of all the elements present in the selected window.

• III.    PROPOSED METHOD

An efficient method for removal high density salt -and - pepper noise with preserving image details is proposed. It is composed of three stages as: (1) Data extraction from the nonnoisy image. (2) Noise detection. (3) Noise cancellation. Figure.1 shows the core idea for the proposed method. The extracted data from the nonnoisy image, as Lena image, is applied in the filter equation to produce filtered image from its noisy image.

Figure.1. The Core Idea for the Proposed Method.

• (1)    Data extraction

• 2.1- Select   3X3 window and place it,

Extracted the data from the nonnoisy image are used in the filter operation to produce filtered image from its noisy image. This is presented in this stage by achieving the following steps:-

2-

Divide the nonnoisy image into non overlapping four blocks.

Repeat the following for each block i ^Э i = ^1,4

randomly, in any area within the block

i

• 2.2- Extract the center pixel value and put it in the first row in the vector Bⁱ .

• 2.3- Extract two nearest neighbors and put

• 2.4- Move, randomly, the window within the block i .

• 2.5- Extract the center pixel value and put it in the second row in the vector Bⁱ

• 2.6- Extract two nearest neighbors and put them in the second row in the matrix ^{A i} .

A them in the first row in matrix i

End

A = £ AJ/4   B = £ BJ/4

• 3-    Compute       i ^{= 1}         and         i ^{= 1}

• 4-    Repeat the following for each block i

• 4.1-    Select 3X3 window and place it randomly in any area within the block i .

• 4.2-    Extract the center pixel value and put it in the first row in the vector B_i .

• 4.3- Extract three nearest neighbors and put them in the first row in the matrix A_i

• 4.4- Move randomly the window within the block i .

• 4.5-    Extract the center pixel value and put it in the second row in the vector B _i

• 4.6- Extract three nearest neighbors and put them in the second row in the matrix A_i .

• 4.7- Move randomly the window within the block i .

• 4.8-    Extract the center pixel value and put it in the third row in the vector B

• 4.9- Extract three nearest neighbors and put them in the third row in the matrix A_i .

End

44 A = ( S A J/4    В = ( S ^Bi )/4

• 5-    Compute        i = 1         and        i = 1

• 6-    Repeat the following for each block i

• 6.1- Select 3X3 window and place it randomly in any area within the block i .

• 6.2- Extract the center pixel value and put it in ˆ

• 6.3- Extract four nearest neighbors and put them

• 6.4- Move randomly the window within the block i .

• 6.5- Extract the center pixel value and put it in ˆ

• 6.6- Extract four nearest neighbors and put them

• 6.7- Move randomly the window within the block i .

• 6.8- Extract the center pixel value and put it in ˆ

• 6.9- Extract four nearest neighbors and put them

• 6.10- Move randomly the window within the block i .

• 6.11-    Extract the center pixel value and put it in ˆ

the first row in the vector ⁱ .

A in the first row in the matrix i

the second row in the vector ⁱ

A in the second row in the matrix i .

the third row in the vector ⁱ

A in the third row in the matrix i .

the fourth row in the vector ⁱ

• 6.12- Extract four nearest neighbors and put

A them in the fourth row in the matrix ⁱ .

End

A = (S Ai)/4   В = (S В^4

• 7-    Compute       i = ¹        and        i = 1

All the matrices and vectors that extracted in this stage are used in filter operation.

• (2)    Noise detection.

Noise detection is the first stage in this method. The salt-and-pepper noise pixels can take the maximum and minimum values in the dynamic range. Therefore, if the value of the processed pixel lies between the maximum and minimum values inside the window, then it kept unchanged. If the value does not lie within this range, then it is a noisy pixel and is replaced by the output of the filter operation.

• (3)    Noise cancellation

Each element in the vectors B , B and B is the desired value for its corresponding row (its neighbors) in the matrices A , A and A , respectively. The goal is to estimate parameters which are obtained the desired values, in vectors, from their corresponding rows in the matrices. The linear systems AX = В , AX = В and ˆˆ   ˆ

• .^A^X — ^B are used to describe the relation between the vectors and their corresponding matrices such that X = A-¹ В ,      X = A -¹ В and X = A "* В . The

vectors X , X and X represent the estimation parameters that are used in the filter operation. Switching between 3X3 and 5X5 window size is used based on the number of noisy pixels where only the noise free pixels are considered in the filter operation. But, if all the pixels inside the 5X5 window are noisy, then replace the processed pixel by the previous resultant pixel. The noise cancellation stage for each pixel location ^{( i , j )} to produce filter image ^g can be achieved by the following steps.

• 1-    Select a 2-D window of size 3X3.

• 2-    Eliminate the noisy pixels within the window.

• 3-    Insert the noise free pixels into vector R .

• 4-    Assign the number of pixels in the R to L .

• 5-    If ( L <  1 ), go to step 10.

• 6-    If ( L = 1 )

  • 6.1    Let g ( i , j ) equal to the pixel value in L

  • 6.2    Return to step 1 for the next ( _{i ,} j )

• 7-    If ( L = 2 )

  • 7.1    g ( i , j ) = L (1). X (1) + L (2). X (2)

  • 7.2    Return to step 1 for the next ( _{i ,} j )

• 8-    If ( ^L = 3)

  • 8.1     g ( i , j ) = L (1). X (1) + L (2). X (2) + L (3). X (3)

  • 8.2    Return to step 1 for the next ^{( i , j )}

• 9-    if ( L >  4 )

• 9.1    L (3). X (3) + L (4). X (4)

• 9.2    Return to step 1 for the next ( i , j )

g ( i , j ) = L (1). X (1) + L (2). X(2) +

• 10-    Increase the window by 5X5.

• 11-    Eliminate the noisy pixels within the window.

• 12-    Insert the noise free pixels into vector ^S .

• 13-    Assign the number of pixels in the ^S to P .

• 14-    If ( P <  1 ), go to step 19

• 15-    If ( P = 1 )

  • 15.1    Let ^{g ( i , j )} equal to the pixel value in P

  • 15.2    Return to step 1 for the next ( i , j )

• 16.1    g ( i , j ) = P (1). X (1) + P (2). X (2)

• 16.2    Return to step 1 for the next ( i , j )

16-1 ( P = 2 )

• 17-    If ( P = 3)

  • ₁₇.1    g ( i , j ) = P (1). X (1) + P (2). X (2) + P (3). X (3)

  • 17.2    Return to step 1 for the next ( i , j )

• 18-    If ( P >  4 )

• ₁₈.1    P (3). X f(3) + P (4). X f(4)

• 18.2    Return to step 1 for the next ( i , j )

  19- Replace pixel.

  
  

  g ( i , j )

  
  

g ( i , j ) = P (1). X (1) + P (2). X(2) +

with the nearest noise free

20 -Return to step 1 for the next ( i , j )

IV. SIMULATION RESULTS

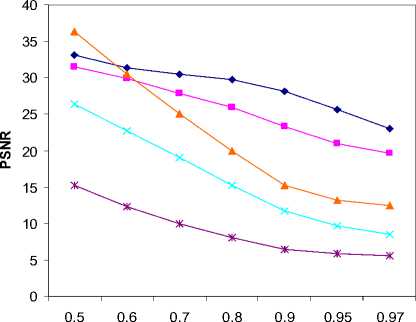
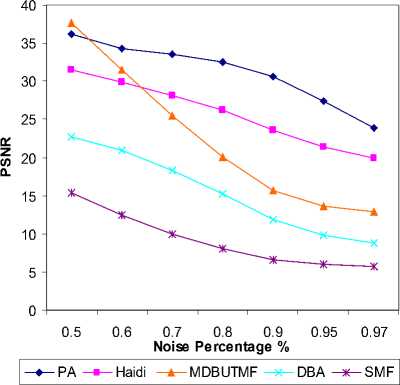
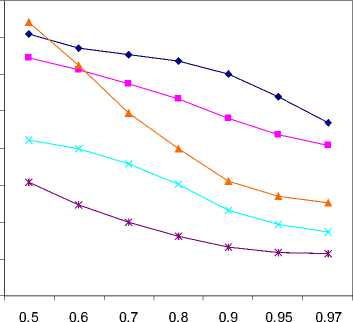
To check the efficiency of the proposed technique, a variety of well-known test images with 1024X1024: Bridge, Boat, Goldhill, and Peppers are used. A wide range of high noise ratios varied from 50% to 97% is tested. Haidi at el method [14], DBA [18], MDBUTMF [19] and standard median filter (SMF) are used in the comparison with the proposed algorithm (PA). Denoising performance is quantitatively measured by the peak signal-to-noise ratio (PSNR) as defined in (1)

PSNR = 10log! ₀ 1 ^255)- ¹⁰ 1 MSE

where MSE stands for mean square error, M _X N is size of the image, F represents the original image and F denotes the denoised image. Table I shows PSNR value of the proposed algorithm (PA) against the existing algorithms by varying the noise density from 50% to 97%. Thus, it is observed that the proposed method gives better PSNR than other existing algorithm. Figure.2 shows a plot of PSNR versus noise densities for Bridge, Boat, Goldhill, and Peppers images. The visual result of the proposed method for Boat image corrupted by 50%, Goldhill image corrupted by 80% and Peppers image corrupted by 97% are shown in Figure.3, Figure.4 and Figure.5, respectively.

££ ( F( i , j ) - F( г , j ) ) 2

MSE = -i—i----------------

M X N

(a) Comparison graph of PSNR at different noise densities for Bridge image.

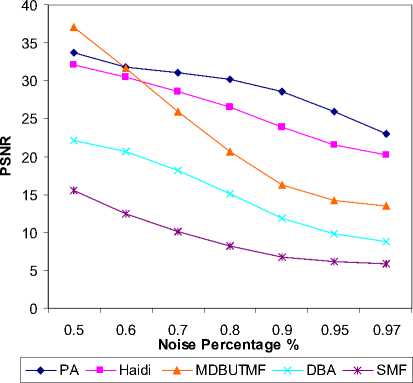
(b) Comparison graph of PSNR at different noise densities for Boat image.

Noise Percentage %

PA Haidi MDBUTMF DBA SMF

• (c)    Comparison graph of PSNR at different noise densities for Goldhill image.

DC

ОТ 20

|^— PA —■— Haidi    MDBUTMF DBA SMF

Noise Percentage %

• (d)    Comparison graph of PSNR at different noise densities for Peppers image.

Figure.2 Comparison Graph of PSNR at Different Noise

Densities for Bridge, Boat, Goldhill and Peppers Images

Table I : COMPARISON OF PROSSING RESULTS IN PSNR (dB) FOR BRIDGE, BOAT, GOLDHILL AND PEPPERS IMAGES.

Bridge
	50%	60%	70%	80%	90%	95%	97%
SMF	15.2561	12.2568	9.9091	7.9927	6.4850	5.8551	5.6152
DBA [18 ]	26.3414	22.6679	19.0508	15.2777	11.7214	9.6453	8.5225
Haidi [14]	31.4620	29.9041	27.7907	25.9067	23.3135	21.0217	19.6282
MDBUTMF[19]	36.3076	30.4300	24.9938	19.8859	15.3091	13.2396	12.4492
PA	33.0957	31.2863	30.4471	29.6731	28.1027	25.6687	22.9920
Boat
SMF	15.4695	12.5225	10.1506	8.2364	6.7249	6.0882	5.8294
DBA [18 ]	22.1797	20.7020	18.2161	15.1558	11.8583	9.8329	8.7985
Haidi [14]	32.0482	30.4337	28.5767	26.5532	23.8427	21.5303	20.2233
MDBUTMF[19]	37.1259	31.7201	25.9988	20.5980	16.2560	14.2292	13.4333
PA	33.6924	31.8605	31.0683	30.1884	28.5687	25.9500	23.0467
Goldhill
SMF	15.3552	12.3908	10.0116	8.0830	6.5889	5.9580	5.7137
DBA [18 ]	22.7533	20.9759	18.3288	15.2281	11.8048	9.7816	8.7662
Haidi [14]	31.4529	29.8889	28.1578	26.1550	23.5644	21.3336	19.9978
MDBUTMF[19]	37.6932	31.4600	25.5095	20.0399	15.7391	13.6901	12.8968
PA	36.2110	34.3507	33.5131	32.5638	30.6643	27.4035	23.9013
Peppers
SMF	15.3275	12.3661	9.9594	8.0579	6.5276	5.8868	5.6543
DBA [18 ]	21.1612	19.9230	17.8101	15.0331	11.6172	9.6086	8.6595
Haidi [14]	32.2007	30.6334	28.6588	26.6614	24.0642	21.8485	20.3038
MDBUTMF[19]	37.0994	31.1429	24.7732	19.9782	15.5061	13.4513	12.6471
PA	35.3872	33.4932	32.6362	31.7422	30.0189	26.9156	23.4969

a) Original Boat image

(a) Original Goldhill image

(b) Boat image corrupted by 50%

(b) Goldhill image corrupted by 80%

(c) The result of PA for corrupted image in (b) Figure 3. The Result of PA for Corrupted Boat Image

(c) The result of PA for corrupted image in (b) Figure 4. The Result of PA for Corrupted Goldhill Image

(a) Original Peppers image

(b) Peppers image corrupted by 97%

(c) The result of PA for corrupted image in (b) Figure 5. The Result of PA for Corrupted Peppers Image

CONCLUSIONS AND PROSPECTS

A new denoising method for removing salt-and-pepper noise is introduced in this paper. This method is simple in implementation where no complex operations are required. The proposed method framework outperforms other existing denoising method for removal of salt - and - pepper noise with preserving image details as it is clearly seen in visual and quantitative results. Moreover, the suggested method presents a quite stable performance over a wide variety of images. In addition, the presented method does not need large data set for training like artificial neural networks and genetic programming, which consuming time for training. Indeed one image is enough for extracting the coefficients, which uses in the filter action. The main advantage of this method is no adjustment of threshold parameters, which influences the behavior of the system.