An Efficient Chaos-based Image Encryption Scheme Using Affine Modular Maps

In recent years, the transmission of digital images over the Internet and wireless networks has been developed rapidly due to the fascinating developments in digital image processing and network communications. It is urgent to protect the communicated image information against illegal usage, especially for those requiring reliable, fast and robust secure systems to store and transmit, such as military image databases, confidential video conference, medical imaging system, online private photograph album, etc. Digital images possess some intrinsic features, such as bulk data capacity and high correlation among adjacent pixels. Therefore most conventional ciphers like DES (Data Encryption Standard), IDEA (International Data Encryption

Algorithm), AES (Advanced Encryption Standard), etc. [1] are not suitable for practical digital image encryption due to the weakness of low-level efficiency while encrypting images. Fortunately, chaos-based image encryption algorithms have shown their superior performance [2-8]. Chaos has been introduced to cryptography thanks to its ergodicity, pseudo-randomness and sensitivity to initial conditions and control parameters, which are close to confusion and diffusion in cryptography. These properties make chaotic systems a potential choice for constructing cryptosystems. Chaosbased image encryption schemes are usually composed of one permutation process and one diffusion process generally. The aim of permutation process is to reduce the high correlation among image pixels, while that of diffusion phase is to change pixel gray values sequentially by diffusion functions so that a tiny change for one pixel can spread out to almost all pixels in the whole image. A good permutation process should show good shuffling effect and a good diffusion process should cause great modification over the cipher-image even if only a minor change for one pixel in the plain-image.

Since Matthews [9] firstly used a chaotic system to design a cryptographic algorithm in 1989, many chaosbased digital image encryption schemes have been proposed in the literature. Among these encryption schemes, one-dimensional and two-dimensional chaotic systems, such as Logistic map, skew tent map, Arnold map, baker map and standard map, were applied widely owing to the advantage of simplicity [5-8,10-12]. However, some chaos-based image encryption algorithms are broken recently due to their small key spaces and weakly secure encryption mechanisms [13-19]. As we know, a good encryption scheme should be sensitive to cipher keys; the key space should be large enough to resist brute-force attack; the permutation and diffusion processes should possess good statistical properties to frustrate differential attack, entropy attack, known-plaintext attack and chosen-plaintex attack, etc. To overcome the drawbacks such as small key space and weakly secure permutation and diffusion architecture in one and two dimensional chaotic systems, many researchers turn to find some improved chaos-based cryptosystems with large key spaces and good diffusion mechanisms. For instance, piecewise nonlinear chaotic algorithm was proposed by Behnia et al. to enhance the security [20]; Zhang et al. recently proposed an image encryption method based on skew tent map and permutation-diffusion architecture [21]. This method generates a P-box with the same size of plain-image and shuffles the positions of image pixels totally; it uses different keystreams depending on plain-image in the diffusion process, so the method is much secure in the sense of preventing chosen-plaintext attack. Zhu et al. [22] proposed a new permutation method at the bit-level, which can confuse and diffuse the image at the same time. Liu and Wang [23] then improved the proposed scheme in [22] to encrypt color image, where the authors permuted the image at the bit-level by mixing all the bits in red, green and blue components. The chaotic map used in the permutation phase is PWLCM instead of Arnold cat map. Other improvements like applying hyper-chaotic differential systems, coupled map lattice system and multi chaotic systems have been investigated and applied to image encryption as well [24-26].

In this paper, a novel image encryption scheme with an efficient permutation-diffusion structure is proposed. In both the permutation process and the diffusion process, chaotic maps are utilized. First, the permutation process employs two affine modular maps to generate two chaotic orbits { x_k , y_k , k = 0 , 1,- •} corresponding to initial conditions    x ₀, y₀    respectively; the      sequence

{xk,k = 1v,Hx W} (H and W are the width and the height of the processed image respectively) and the sequence {yk, k = 1, • • •, H x W}   are then sorted to yield two index order sequences applied to permute the image pixel positions totally. To improve the diffusion effect, a two-way diffusion process is presented, where another two affine modular maps are utilized to generate two pseudo-random gray value sequences. The two sequences are then used to modify the pixel gray values sequentially. The yielded gray value sequences are not only sensitive to the control parameters and initial conditions of the considered chaotic maps, but also strongly depend on the plain-image processed, therefore the proposed scheme can resist statistical attack, differential attack, known-plaintext attack as well as chosen-plaintext attack. The proposed image encryption scheme also possesses large key space, therefore efficiently frustrating brute-force attack.

The rest of the paper is organized as follows. In Section II, affine modular map and its chaotic feature are introduced. Section III proposes a novel chaos-based image encryption scheme composed of one permutation process and one diffusion process. The security of the proposed scheme is evaluated via detailed analysis and experiments in Section IV. Finally, conclusions are drawn in Section V.

• II.    The affine modular map

  Linear congruential generator (LCG) has been used widely since Lehmer initially in 1951 proposed the original algorithm [27]. The linear congruential generator is based on the formula

x „₊1= a x x_n + c mod M , n = 0 , 1, • ••            (1)

where M is the modulus usually chosen to be the largest prime number less than the computer’s word size and the multiplier a , the increment c and the seed x are integer values between 1 and M — 1 . The extended version of LCG acting on real numbers may be written as x_{n + 1} = B ( x_n ) = x n + c mod 1 , n = 0 , 1,---        (2)

a where the control parameters a e (0,0.5], c e [0,1) and the state values xn, xn+1 belong to [0,1) . We shall call it affine modular map. As c = 0, a = 0.5 , map (2) becomes the well-known regular Bernoulli shift map B0 : [0,1] ^ [0,1] given by xn+1 = B0(xn ) := 2xn mod 1

• f    2 X n , if X n e [0 , 1 / 2)            (3)

= S

[ 2 X n — 1 ,    if X n e [1 / 2 , 1]

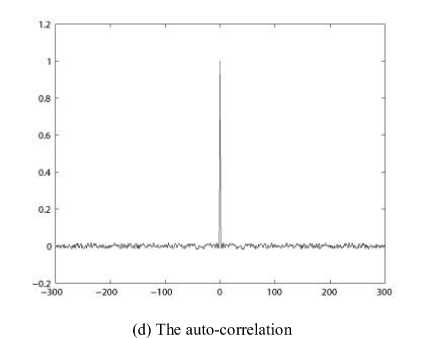
The Bernoulli shift map yields a simple example for an essentially nonlinear stretch-and-cut mechanism, as it typically generates deterministic chaos. Such basic mechanisms are also encountered in more realistic dynamical systems. A typical orbit of x derived from the dynamical system is {xk = Bk (xo ), k = 0,1,- ••} , which    is     shown    in    Fig.     1(a)     for x0 = 0.2709, a = 0.311, c = 0.761. Its waveform is quite irregular and indicates that the system is chaotic. The control parameter a, c and the initial condition x0 can be regarded as cipher keys as the map is used to design image encryption schemes. The bifurcation diagrams of map (2) are shown in Fig. 1(b)-(c) for the parameters a and c respectively, where for each value of a or c , 300 orbit points are plotted. There also exist some good dynamical features in affine modular maps, such as desirable auto-correlation and cross-correlation features. The iterated trajectory is used to calculate the correlation coefficients, which are shown in Figs. 1(d)-(e) respectively. The cross-correlation coefficients are calculated by the orbits of xo = 0.2709 and Уо = 0.3329.

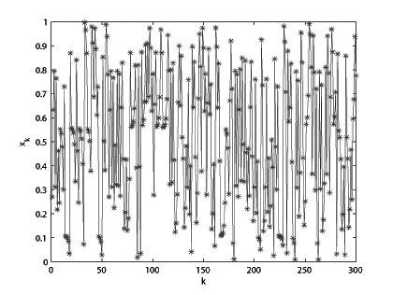
(a) The chaotic orbit of X^ — 0 . 2709

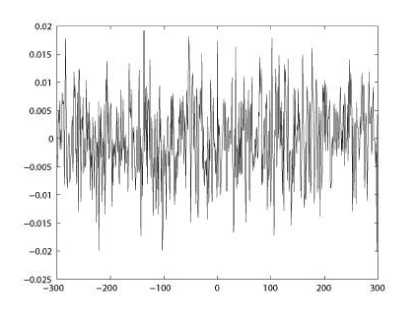
(e) The cross-correlation of two different orbits

Figure 1. Orbit derived from the considered affine modular map with a — 0 . 311 , c — 0 . 761 and the bifurcation diagrams.

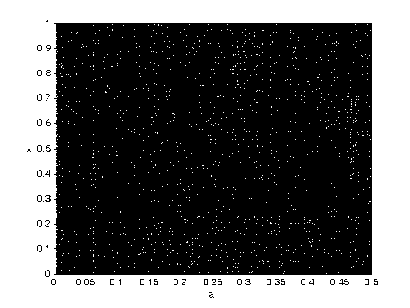
vs a with fixed C — 0 . 23 11

(b) Bifurcation diagram for x

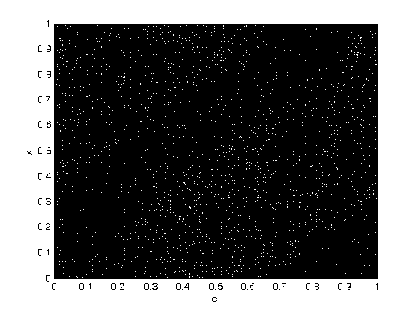
(c) Bifurcation diagram for X^ vs C with fixed a — 0 . 301

• III.    The image encryption scheme based on affine

MODULAR MAPS

• A.    Permutation process

In this subsection, we propose a permutation process to confuse plain-image totally. Thanks to the chaotic nature of affine modular map on the unit interval [0 , 1] , one can easily get the chaotic orbit { x_k , k — 0 , 1,- •} of x ₀ with given control parameters a , c . We rearrange all the x_k values of the orbit to get a new sequence { x _k , k — 0 , 1 ,- • •} according to the order from small to large. As a result, we then get an index order number for every x . The index order number sequence can be applied to permute the image pixel positions and therefore can confuse the image to get a shuffled image. The permutation process is stated as follows.

Pixel permutation scheme:

Step 1. Set the values of the control parameters a. , C. (i — 1 , 2) and the initial condition x ₀, y₀ .

Step 2. Iterate the affine modular map with control parameters a , c_x and initial condition x₀ to get a truncated orbit of x₀ , say { x_k , k — 0 , 1 , • • •, H — 1} . Same operations are performed to get a truncated orbit { y_k , k — 0,1, • • • , W — 1} by iterating the affine modular map with control parameters a ₂, c ₂ and initial condition y ₀ .

Step 3. Sort

{Xk, k — 0,..., H—1},{yk, k — 0,..., W—1} to get two index order sequences {Ixk, k — 0, • • •, H — 1} and {Iyk,k — 0,-**,W — 1}.

Step 4. Permute the pixel gray values matrix A by Ix , ly in the following way to get a shuffled image S :

5 (i , j ) = A(Ix„ j i = О ,---, H - 1 , j = О ,---, W - 1 .

• B.    Diffusion process

It is necessary that a secure encryption algorithm should have a good mechanism of diffusion. On one hand, the diffusion processing can render the permutation process non-invertible, which therefore strengthens the security. On the other hand, the diffusion processing can significantly change the statistical properties of the plainimage by spreading the influence of each bit of the plainimage all over the cipher-image. Though the permutation process has changed the pixel positions of the plainimage, it can not change the histogram of the plain-image. The diffusion process will enhance the resistance to statistical attack and differential attack greatly, in which the histogram of the cipher-image is fairly uniform and is significantly different from that of the plain-image. The opponent can not find any useful clues between the plainimage and the cipher-image and so can not break the cryptosystem even after they spend a lot of time and effort. A good diffusion process should also yield keystreams strongly related to plain-images. When encrypting different plain-images (even with the same cipher keys), the encryption scheme should generate different keystreams. The diffusion process is outlined as follows.

Pixel gray value diffusion scheme:

Step 1. Applying the permutation process to confuse the plain-image A and get a shuffled image S . Set the values of the control parameters a. , q (i = 3 , 4) and the initial condition z ₀, w ₀ for the affine modular maps in the diffusion process.

Step 2. Let i = 0 .

Step 3. Apply the following quantization formula to yield one 8-bit pseudo-random gray value d ( i ) :

d (i) = floor( L x z.)

where L is the color level (for a 256 gray-scale image, L = 256 ), the “floor" operation on x returns the largest value not greater than x .

Step 4. Compute the pixel gray value in the cipherimage by a two-point diffusion transmission:

C (i +1) = ^(i +1) e [(d (i) + C (i ))mod L ],     (4)

where ф (i + 1) is the gray value of the current operated pixel in the shuffled image which has been rearranged according to the order of row or column to a vector with length H x W , C ( i ) is the previous output cipher-pixel gray value. The diffusion process is well defined as the initial condition C (0) is provided. C (0) can be set to be part of the keys in the diffusion process or can just take the value of d (0) for simplicity.

Step 5. Compute s by s = 1 + [C(i + 1)mod 2] to get the next z by iterating the affine modular map with control parameters a3, c3 on z. for s rounds, that is, z^t = B (zt) . This is the crucial step to generate a keystream depending on the plain-image since s is related to C(i +1), so is z^t. The encrypted image not only relates to the cipher keys, but also relates to the plain-image.

Step 6. Let i = i + 1 and return to Step 3 until i reaches H x W .

The above diffusion process implies that it can not influence the pixels before the tampered pixel with a gray value change. As a remedy, we here add a reverse diffusion process as a supplement to the above diffusion process. Another affine modular map with control parameters a ₄, c ₄ is used here.

Step 7. Iterate the following affine modular map to produce another pseudo-random gray value sequence

wk+1 = B (wk)>

И k +1) = floor( L x wk+J, k = 0,1,-, H x W -1.

Step 8. Execute the reverse diffusion process:

D (i) = D (i +1) e [(C (i) + v(i))mod L ], i = Hx W ,-, 2,1,                   (5)

where D(i), i = 1,2, • • •, H x W are the final encrypted vector consisting of the encrypted image pixel gray-scale values. The value of D(H x W +1) should be provided to cipher out the sequence D(i), i = 1,2, • • •, H x W .

D ( H x W + 1) can handled in the same way as C (0) . The complete diffusion process is composed of Step 1 to Step 8.

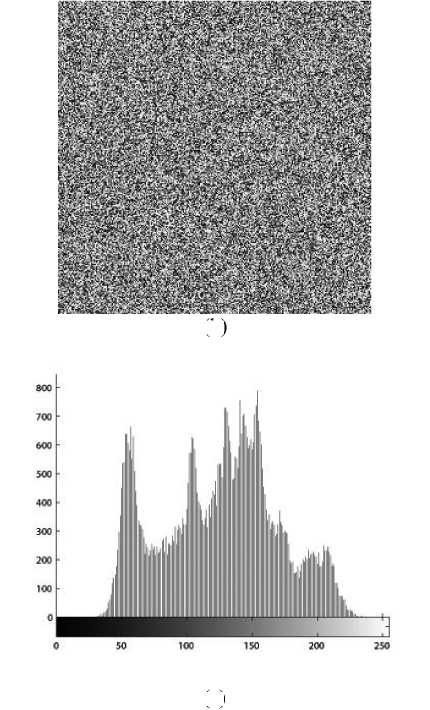
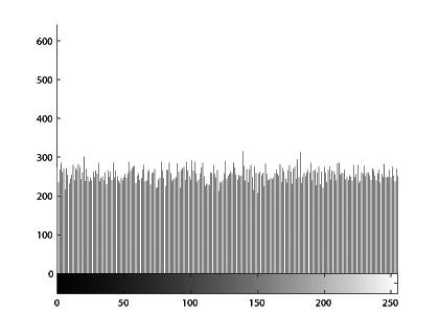
The permutation process and the diffusion process form the proposed image encryption scheme. The original image Lena is encrypted and the result is shown in Fig. 2(b). We choose the plain-image Lena sized 256 x 256 . Fig. 2 shows the encryption results. The cipher keys are ax = 0.23, a2 = 0.37, q = 0.31, c2 = 0.81,

x0 = 0.2709, y0 = 0.7507, a3 = 0.3216, a4 = 0.3902, c3 = 0.73, c4 = 0.67, z0 = 0.7627, w0 = 0.3607.

(a)

(b)

and differential analysis. All the analysis shows that the proposed image encryption scheme is highly secure.

A. Key space analysis

A good image encryption scheme needs to contain sufficiently large key space for compensating the degradation dynamics in PC. It should be sensitive to cipher keys as well, and thus can effectively prevent invaders decrypting original data even after they invest large amounts of time and resources. The analysis results regarding the sensitivity and the key space are summarized as follows. Since the permutation process is irrelevant to the diffusion process, the key space consists of the cipher keys in both processes. Therefore, the control parameters a_t , c. (i = 1, • • • , 4) and the initial

condition x ₀, y ₀, z ₀, w ₀ constitute the cipher keys. The sensitive tests with respect to all cipher keys have been carried out. To verify the sensitivity of key parameter K , the original plain-image I = ( I(i, j))_HxW is encrypted

with K = p , K = p — A 5 and K = p + A 5 respectively while keeping the other key parameters unchange. The corresponding encrypted images are denoted by | , I ₂, I₃ respectively. The sensitivity

(c)

(d)

Figure 2. The encryption results. (a) plain-image, (b) cipher-image

(c) Histogram of original image, (d) Histogram of encrypted image

coefficient to the parameter K is denoted by following formula [6]:

Ps(K) = T"^ £ [N. (11(ij) 12(ij))

2 x H x W ту

, j

+ N. (I,(i, j ), Iз( i, j ))] x100 % where

N.(x, У )

= <

1 ,

I0,

X * У , x = y ,

the

and A 5 is the perturbing value. P ( K ) implies the

sensitivity to the perturbation of parameter K . The greater of P ( K ) , the more sensitive for the parameter K . Table 1 shows the results of the sensitivity test where the initial key values are set to be the following( N = N = N₂ = 6 ): Permutation process:

x ₀ = 0 . 2709 , y ₀ = 0 . 7507 , a = 0 . 23 , a ₂ = 0 . 37 ,

• IV.    Security analysis

According to the basic principle of cryptology [1], a good encryption scheme requires sensitivity to cipher keys, i.e., the cipher-text should have close correlation with the keys. An ideal encryption scheme should have a large key space to make brute-force attack infeasible; it should also well resist various kinds of attacks like statistical attack, differential attack, etc. In this section, some security analysis has been performed on the proposed image encryption scheme, including the most important ones like key space analysis, statistical analysis, c = 0.31, c2 = 0.81,

Diffusion process:

z ₀ = 0 . 7627 , w₀ = 0 . 3607 , a, = 0 . 3216 ,

• a, = 0 . 3 902 , c ₃ = 0 . 73 , c ₄ = 0 . 67 .

The variations A 5 of the considered parameters are shown in below:

x0 = ax = a2 = c = c2 = 10-16, y0 = 10-15,z0 = w0 = a3 = a4 = c3 = c4 = 10-16.

We apply the proposed image encryption scheme one round with only perturbing one cipher key K with the corresponding variation value while fixing other parameters.

Table 1. Results regarding the sensitivity to cipher keys.

K	x 0	y 0	a	a	c 1	c 2
P s ( K )	0.9961	0.9963	0.9961	0.9961	0.9960	0.9959
K	z 0	w 0	a 3	a 4	c 3	c 4
P s ( K )	0.9959	0.9959	0.9963	0.9963	0.9959	0.9963

(b) Encrypted image with a_x = 0 . 23 , y ₀ = 0 . 3607

The results in Table 1 imply that the control parameters a_t , c_t (i = 1<^ee, 4) and the initial conditions x _o, y₀ , z ₀, W _o are all strongly sensitive. It also implies from the results that the key space is more than 10¹⁹¹ , which is large enough to make brute-force attack infeasible. The sensitivity tests can also be demonstrated visually, for example, see Figs. 3-4. In Fig. 3, the encrypted image with the key a ₁ = 0 . 23 has 99.60% of difference from the encrypted image with the key a_x = 0 . 23 + 10 - 16 ; the image encrypted by the key y ₀ = 0 . 3607 has 99.67% of difference from the image encrypted by the key y ₀ = 0 . 3607 + 10 ^{- 16} . Fig. 4 shows that the image encrypted by a ₃ = 0 . 3216 , y ₀ = 0 . 3607 is not correctly decrypted by using the perturbed key a ₃ = 0 . 3216 + 10 ^{- 16} , y ₀ = 0 . 3607 . The same conclusion holds with the keys

(c) Encrypted image with a_x = 0 . 23 + 10 ¹⁶ , y ₀ = 0 . 3607

(d) Difference image between (b) and (c)

a3 = 0.3216, y0 = 0.3607 +10“16.

(a) plain-image Lena

(e) Encrypted image with a = 0 . 23 , y₀ = 0 . 3607 + 10 ¹⁶

(b) Decrypted image with a ₃ = 0 . 3216 , y ₀ = 0 . 3607 + 10 ¹

Figure 4. Key sensitive test: result 2.

(f) Difference image between (b) and (e) Figure 3. Key sensitive test: result 1.

(a) Decrypted image with a ₃ = 0 . 3216 + 10 ¹⁶ , y ₀ = 0 . 3607

• B.    Statistical analysis

Shannon pointed out in his masterpiece [28] the possibility to solve many kinds of ciphers by statistical analysis. Therefore, passing the statistical analysis on cipher-image is of crucial importance for a cryptosystem. Indeed, an ideal cryptosystem should be highly robust against any statistical attack. In order to prove the security of the proposed encryption scheme, the following statistical tests are performed.

• (i)    Histogram. Encrypt the image Lena with one round, and then plot the histograms of plain-image and cipherimage as shown in Figs. 2(c)-(d), respectively. Fig. 2(d) shows that the histogram of the cipher-image is fairly uniform and significantly different from the histogram of the original image and hence it does not provide any useful information for the opponents to perform any effective statistical analysis attack on the encrypted image.

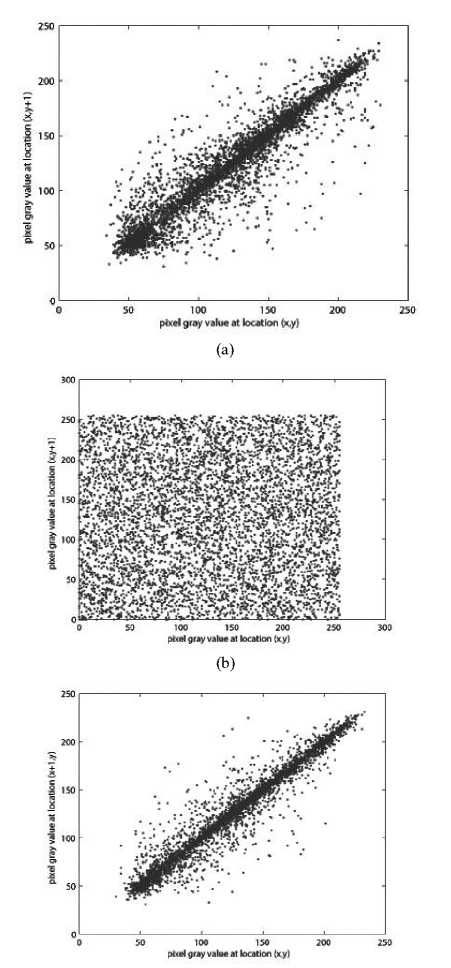
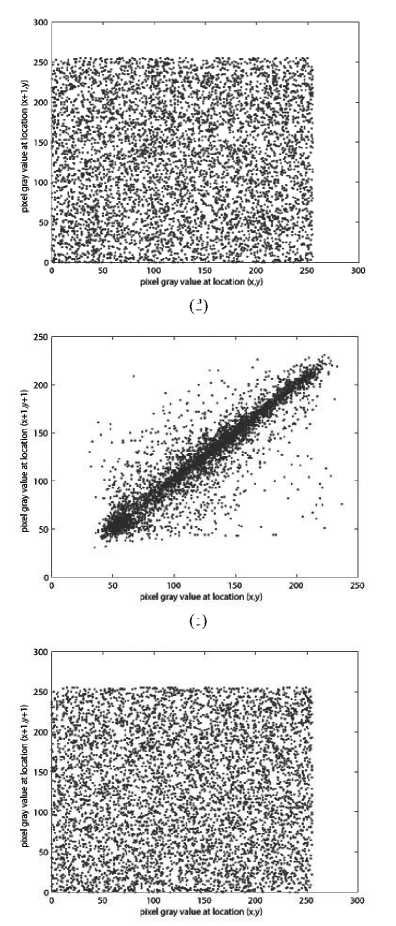
• (ii)    Correlation of adjacent pixels. To test the correlation between two adjacent pixels, the following performances are carried out. First, we select 6000 pairs of two adjacent pixels randomly from an image and then calculate the correlation coefficient of the selected pairs using the following formulae:

cov ( X , y )

Cr = D5(x) .jD^y) ,

T

cov(x, y) = T X (x - E(x))(yi - E(y)), i=1

TT

E(x) = T X xi, D(x) = T ^ (Xi - E(x))2, i=1                            i=1

where X , y are the gray-scale values of two adjacent pixels in the image and T is the total pairs of pixels randomly selected from the image. The correlations of two adjacent pixels in the plain-image and in the cipherimage are shown in the Table 2.

Table 2. Correlation coefficients of two adjacent pixels in two images.

	Plain-image	Cipher-image
Horizontal	0.9435	0.0128
Vertical	0.9680	0.0098
Diagonal	0.9157	0.0215

The correlation distribution of two horizontally adjacent pixels in the plain-image and that in the cipherimage is shown in Fig. 5.

(c)

(d)

(e)

(f)

Figure 5. Correlations of two adjacent pixels in the plain-image and in the cipher-image: (a), (c), (e) are for the plain-image; (b), (d), (f) are for the cipher-image.

• (iii)    Information entropy analysis. The entropy is the most outstanding feature of randomness. The entropy H ( m ) of a message source m can be measured by

L - 1

H(m) = -^ p(m. )lOg(p(m.)) i=0

where L is the total number of symbols m , p ( m ) represents the probability of occurrence of symbol m and log denotes the base 2 logarithm so that the entropy is expressed in bits. For a random source emitting 256 symbols, its entropy is H ( m ) = 8 bits. For the encrypted image of Lena, the corresponding entropy is 7.9965 bits. This means that the cipher-image is close to a random source and the proposed algorithm is secure against the entropy attack.

• C.    Differential attack

In general, attacker may make a slight change (e.g., modify only one pixel) of the plain-image to find out some meaningful relationships between the plain-image and the cipher-image. If one minor change in the plainimage will cause a significant change in the cipher-image, then the encryption scheme will resist the differential attack efficiently. To test the influence of only one-pixel change in the plain-image over the whole cipher-image, two common measures are used: number of pixels change rate (NPCR) and unified average changing intensity (UACI). They are defined as

У  D (i, j)

NPCR =   -----x 100 %,

W x H

UACI =       [У | C1(i’j) - C2(i’j)|]x 100%

W x H       255

where C , C₂ are the two cipher-images corresponding to two plain-images with only one pixel difference, W and H are the width and height of the processed image, D is a bipolar array with the same size as image C . D ( i, j ) is determined as: if C ( i , j ) = C₂ (i , j ) , then D ( i , j ) = 0 , otherwise D ( i , j ) = 1 .

NPCR measures the percentage of different pixels numbers between the two cipher-images whose plainimages only have one-pixel difference. UACI measures the average intensity of differences between the two cipher-images. To resist difference attacks, the values of NPCR and UACI should be large enough. The test of the plain-image is the “all-zero" image. We randomly select 10 pixels and change the gray values with a difference of 1, for example, we replace the gray value 0 of the pixel at position (29,142) by 1, and get the NPCR=99.6933%, UACI=31.1672%. The numerical results are shown in Table 3. The mean values of the ten NPCR and UACI values are 99.8232% and 37.6615% respectively. We observe from Table 3 that the two measure values are exceptionally good undergoing only one round of encryption.

Table 3. Results of NPCR and UACI tests of Lena.

Position	(29,142)	(18,64)	(195,103)	(80,91)	(210,65)
NPCR(%)	99.6933	99.9344	99.8444	99.7574	99.6994
UACI(%)	31.1672	48.0636	44.6477	30.6300	29.2835
Position	(40,27)	(111,105)	(62,129)	(199,8)	(2,76)
NPCR(%)	99.8810	99.8779	99.8138	99.7879	99.9420
UACI(%)	45.3833	28.2749	41.9523	29.6468	47.5657

• D.    Resistance to known-plaintext and chosen-plaintext attacks

In the diffusion process, a feedback from the cipherimage is employed to change the number of iterations of the generalized multi-sawtooth map. In Step 3, d(i) depends on the value of y which is related to the plainimage, implying that the keystream depends on the processed image. When different plain-images are encrypted, the corresponding keystreams are not the same. The attacker cannot obtain useful information by encrypting some special images since the resultant information is related to those chosen-images. Therefore, the attacks proposed in Refs. [16,17,19] become ineffective on this new scheme. The proposed scheme can desirably resist known-plaintext attack and chosen-plaintext attack.

• V. Conclusions

An efficient image encryption scheme based on affine modular maps is proposed in the paper. The proposed scheme can shuffle the plain-image efficiently in the permutation process. An effective two-way diffusion process is also presented to change the gray values of the whole image pixels. Security analysis including key space analysis, statistical attack analysis and differential attack analysis are performed numerically and visually. All the experimental results show that the proposed encryption scheme is secure thanks to its large key space, its highly sensitivity to the cipher keys and plain-images. The proposed encryption scheme is easy to manipulate and can be applied to any images with unequal width and height as well. All these satisfactory properties make the proposed scheme a potential candidate for encryption of multimedia data such as images, audios and even videos.

Acknowledgment

This research was partially supported by the NNSF of China (No. 60863010) and NSF of Xinjiang Province (No. 2010211a19).