An Efficient Feature Selection based on Bayes Theorem, Self Information and Sequential Forward Selection

Published Online November 2016 in MECS DOI: 10.5815/ijieeb.2016.06.06

Feature Selection (FS) is an effective pre-processing technique commonly used in data mining, machine learning and artificial intelligence in reducing dimensionality, removing irrelevant and redundant data, increasing learning accuracy and reducing the unnecessary increase of computational cost [10]. Large number of features given as input to the classification algorithms may lead to insufficient memory and also require more time for learning. The features which do not have any influence on the target is said to be irrelevant. The irrelevant features present in the original feature space will produce more classification errors and sometimes may produce even worse results. Thus it is essential to select the more relevant features which will provide useful information to the target and it can be performed through FS.

Feature relevance is classified into three categories viz., strongly relevant, weakly relevant and irrelevant. A strongly relevant feature is always necessary for the optimal subset and it cannot be removed. A feature is said to be weakly relevant if it is necessary for an optimal subset only at certain conditions. An irrelevant feature is one which is not necessary at all and hence it must be removed. Thus an optimal subset of features should include all strongly relevant, a subset of weakly relevant and none of the irrelevant features [2].

This paper focuses on finding the strongly relevant features from the feature space and comprises two phases viz., Feature Weighting (FW) and Feature Selection (FS). Also it integrates the metrics viz., Bayes Theorem (BT) and Self Information (SI) for FW and Sequential Forward Selection (SFS) for FS. The SFS considers the optimal subset to be empty initially and adds features one by one until the best feature subset is obtained.

The objective of the proposed work is to enhance the predictive accuracy of the Naive Bayesian Classifier (NBC) with limited subset of selected features. The NBC is a statistical classifier based on BT. Since the Bayesian analysis suffers from high computational cost especially in models with a large number of features and to reduce the model construction time of NBC, this work uses BT in the pre-processing step in finding the more relevant features.

The rest of the paper is organized as follows. Section 2 depicts the related work. The mathematical background necessary for understanding the proposed work is explained in Section 3. Section 4 describes the proposed methodology. The experimental study and their results are shown in Section 5. Finally, Section 6 ends with conclusion.

II.    Related Work

Research in improving the accuracy of the classifier is a common issue and is in high demand today. An important problem related to mining large datasets both in dimension and size is of selecting a subset of original features using FS. It is essential that, the reduced set should retain the optimal salient characteristics of the data not only by decreasing the processing time but also leads to more compactness of the models learned and better generalization. Several FS algorithms have been proposed in literature but this section presents a brief overview of them which provides a stronger lead to the proposed work.

Mark A. Hall (2000) has described a Fast Correlation Based Filter (FCBF) for discrete and continuous cases and it is proved that there is a drastic reduction of attributes and outperformed well than ReliefF [1]. Lei Yu and Huan Liu (2004) introduced a new framework for FS called FCBF, which combines feature relevance and redundancy analysis. It uses Symmetric Uncertainty (SU) for both relevance and redundant analysis and they achieved a high degree of dimensionality reduction and also demonstrated that the predictive accuracy with selected features are either enhanced or maintained [2].

A FS method has been proposed by Jacek Biesiada and Wlodzislaw Duch (2007) using Pearson Chi-Square test for nominal (discretized) features particularly for finding redundant features and proved that it provides better accuracy [4]. Subramanian Appavu et al., (2009) have proposed a FS method for finding dependent attributes from the datasets using the joint probabilities with BT and proved that it provides better accuracy [6]. Gauyhier Doquire and Michel Verleysen (2011) have described a FS method based on Mutual Information for handling mixed type of data using both wrapper and filter and proved that it finds more relevant features than Correlation based Feature Selection (CFS) [7].

Subramanian Appavu et al., (2011) have proposed a FS method using BT and IG. They discovered the dependant attributes from the feature space using BT and removing the feature which has high IG as the redundant attribute and further proved that the accuracy has been increased significantly for the classifiers such as C4.5 and Naive Bayes [8]. John Peter and Somasundaram (2012) have launched a novel FS method by combining CFS and BT. The CFS algorithm reduces the number of attributes by SU. The selected attributes from CFS is again fed into BT for selecting the optimal subset of features and they proved that it provides better accuracy than the traditional algorithms [9].

Rajeshwari et al., (2013) has initiated a FS method using Principal Component Analysis (PCA) and Apriori based association rule mining and showed that Apriori gives 100% accuracy for the selected features and PCA requires more time for building model [10]. Mani and Kalpana (2015) have proposed a filter based FS method using Information Gain (IG) with Median Based Discretization (MBD) for continuous features and proved that it provides high accuracy than IG with standard unsupervised discretization methods viz., Equal Width Interval Discretization (EWID), Equal Frequency Interval Discretization (EFID) and Cluster Based Discretization (CBD) particularly for Naive Bayesian Classifier [11].

Muhammad Atif Tahir et al., (2007) has introduced a Tubu Search method for simultaneous feature selection and feature weighting using K-NN rule and proved that it provides high classification accuracy and also reduces the size of the feature vector [15].

From the existing literatures, it is noted that no authors have proposed a feature weighting method by amalgamating BT and SI. But some authors have utilized BT only to deduct dependency among the features and not for finding feature relevance. Thus the proposed work uses MBD for continuous features, BT and SI for FW and SFS for FS.

III.    Mathematical Preliminaries

This section presents an overview of the mathematical concepts which are essential for the proposed work.

• A.    Bayes Theorem

Bayes theorem describes usage of conditional probability with a set of possible causes for a given observed event. It is computed from the knowledge of the probability of each cause and the conditional probability of the outcome of each cause. It relates the conditional and marginal probabilities of stochastic events A and B. It is stated as

P ( A ) P ( B | A )

P ( A | B ) =

P ( B )

Where i) P(A) and P(B) are the prior or marginal probability of A and B respectively. ii) P(A|B) is the conditional probability of A, given B and it is called the posterior probability because it is derived from B. iii) P(B|A) is the conditional probability of B , given A and it is called the prior probability. In general, the BT is stated as [6]

P ( Ai I B ) =

P ( A_i ) P ( B | A_i ) nP ( A ) P ( B\A ) i = 1 i             i

• B.    Measure of Self Information

Let a discrete random variable X with the possible outcomes X = x_i , i = 1, 2, 3, ... , n , then the measure of Self Information of the event X = x_i is defined as [5]

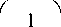
I ( xi) = log₂

- log2 P ⁽ xi)        (3)

From (3), it is noted that the high probability event conveys less information than that of a low probability event and vice versa. i.e., for an event with P(x_i) = 1 then I(x i )=0 .

• C.    Naive Bayesian classifier

It is a statistical classifier based on the Bayes Theorem. Let D be a set of training tuples with class label C . Suppose there are m distinct classes C 1 ,C 2 ,…,C m . The role of this classifier is to predict that the given tuple X belongs to the class having the highest posterior probability contained on X. i.e., the tuple X belongs to C i iff P ( C | X ) >  P ( C | X ) for 1 <  j < m and j + i . P ( C i | X ) is computed as [3]

P ( Ci | X ) =

P ( C_i ) P ( X | C_i ) P ( X )

• D.    Evaluation Measures

Performance of the classifier can be analyzed using the most widely used metrics viz., Accuracy, Precision and Recall [3]. Accuracy is the percentage of test tuples that are correctly classified by the classifier [3] [14]. Precision is a measure of exactness and Recall is a measure of completeness. These measures are computed as [3] .

TP + TN

Accuracy =------------------ (5)

TP + TN + FP + FN

TP

Precision =-------- (6)

TP + FP

Where True Positive (TP) and True Negative (TN) refer to the positive and negative tuples that are correctly identified by the classifier respectively, False Positive (FP) and False Negative (FN) refer to the negative and positive tuples that are incorrectly classified by the classifier respectively [3] [14].

IV.    Proposed Work

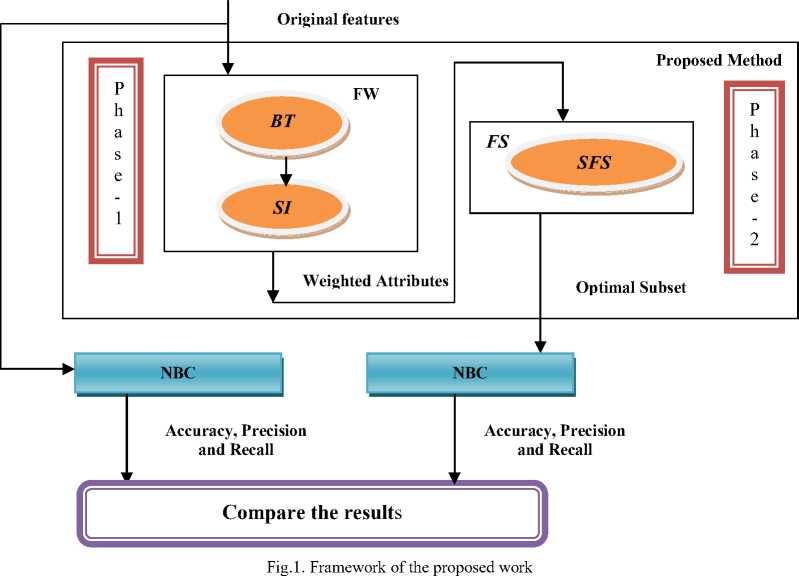
The main idea of the proposed work is to find the strongly relevant features from the feature space so as to improve the predictive accuracy, precision and recall of the NBC. It consists of two phases viz., FW and FS. First it converts the continuous attributes if any in the given dataset into discrete using MBD. After converting, the resultant dataset is fed into FW process. It assigns different weights to attributes based on the results of the computation of BT and SI. Finally the weighted attributes are given to SFS, which selects the features which have the weight greater than the user defined threshold δ. i.e., the more relevant features have higher weight. Performance of the proposed work is analyzed with NBC using the measures viz., accuracy, precision and recall. The optimal feature subset SF_opt obtained are fed into NBC for determining the above said measures and results are analyzed.

The framework of the proposed work is shown in Fig. 1. The steps involved in the proposed work are shown in algorithms 1 and 2. Algorithm 1 calculates the feature weight for each attribute using BT and SI. The features whose weight exceeds the threshold are selected to form the final subset SF opt and it is shown in algorithm 2.

TP

Recall =-------- (7)

TP + FN

Algorithm 1: Feature Weighting using BT and SIInput

Training set TS with 'n' attributes F i , 1 ≤ i ≤ n , each with 'r' instances and 'y' distinct values and a target attribute C with 'm' distinct values.

Output

Weighted feature list

Method

• 1.    For each continuous attribute F_i in T S , use MBD to convert it into discrete

• a)    Compute Median M

• i.    Sort the values of a continuous feature F_i in ascending order

• ii.    For each unique value x i in F i , calculate the frequency of occurrence f and cumulative frequency cf

• iii.    Mid ← (N+1)/2 where N=∑f

• iv.    The item which has cf ≥ Mid is M.

• b)    Perform discretization

F i_des ←{ low,high }

For each xi ∈ Fi if xi > M

Where W is the weight of the feature F_i

Algorithm 2: Select the relevant features from W 's using SFS

Input

Weighted attribute list W 's and the user defined threshold δ

Output

An optimal subset SF opt

Method

• 1.   SF opt ← Ø

• 2.    For each attribute F i ∈ TS

if W ≥ δ then

F _i

SF opt ← SF opt ∪ {F i }

• A. Proposed work - An Example

• 2.    For each feature F i , 1 ≤ i ≤ n and the unique value in the class label C k , 1 ≤ k ≤ m , compute P(C|F i )

  a)

  
  

To show the relevance of the proposed work, the weather dataset has been taken from UCI machine learning repository. The dataset comprises 5 fields, out of which 2 are continuous and 3 are discrete. The dataset contains 14 instances. The target attribute contains two distinct values 'yes' and 'no'. The entire content of the weather dataset is shown in table 1.

then x i ← F i_des [1]

else x i ← F i_des [0]

^P ( C_k ) x ^p ( Fi \c_k )

P(ck 1 Fi) *--k---------------- k               P(Fi)

p ( c i f ) + p ( c ₂i f ) + ... + p ( c \ f )

• b) P ( C I F ) *--1--- i -------²--- i-----------m---—

  P ( F_i )

  
  

• 3.    Compute Self Information for P(C|F_i) , 1≤ i ≤ n

Where

For each feature F i , 1≤ i ≤ n

For each unique instance u l in F i, 1≤ l ≤ y count ( u )

^P ( Flu, ) *^L l_r

Also Z P ( Fiu_t ) = 1

^a)    W_Fj * log₂

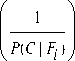
*- log2 P ( C\Fi )

Table 1. Weather Dataset

Outlook	Temperature	Humidity	Windy	Play
Sunny	85	85	FALSE	No
Sunny	80	90	TRUE	No
Overcast	83	86	FALSE	Yes
Rainy	70	96	FALSE	Yes
Rainy	68	80	FALSE	Yes
Rainy	65	70	TRUE	No
Overcast	64	65	TRUE	Yes
Sunny	72	95	FALSE	No
Sunny	69	70	FALSE	Yes
Rainy	75	80	FALSE	Yes
Sunny	75	70	TRUE	Yes
Overcast	72	90	TRUE	Yes
Overcast	81	75	FALSE	Yes
Rainy	71	91	TRUE	No

The median of the attribute 'Temperature' is 72 based on step 1(a) of algorithm 1 and it is illustrated in table 2. After finding the median, the 'Temperature' is discretized as {High, High, High, Low, Low, Low, Low, Low, Low, High, High, Low, High, Low} based on step 1(b) of algorithm 1. Similar calculations are performed for other continuous attributes in the dataset. Table 3 shows the complete content of weather dataset after MBD.

Table 2. Calculation of Median

Unique values of Temperature	Frequency of occurrence	Cumulative frequency
64	1	1
65	1	2
68	1	3
69	1	4
70	1	5
71	1	6
72	2	8
75	2	10
80	1	11
81	1	12
83	1	13
85	1	14

Table 3. Weather Dataset after MBD

Outlook	Temperature	Humidity	Windy	Play
Sunny	High	High	False	No
Sunny	High	High	True	No
Overcast	High	High	False	Yes
Rainy	Low	High	False	Yes
Rainy	Low	Low	False	Yes
Rainy	Low	Low	True	No
Overcast	Low	Low	True	Yes
Sunny	Low	High	False	No
Sunny	Low	Low	False	Yes
Rainy	High	Low	False	Yes
Sunny	High	Low	True	Yes
Overcast	Low	High	True	Yes
Overcast	High	Low	False	Yes
Rainy	Low	High	True	No

Computation ofW :

F = {Outlook, Temperature, Humidity, Windy, Play}

Outlook={Sunny,Overcast,Rainy}

Temperature={High,Low}

Humidity={High, Low}

Windy={TRUE, FALSE}

Play={Yes, No}

P(Yes)=9/14=0.642857

P(No)=5/14=0.357149

Finding feature weight for the feature 'Outlook' with the target 'Play':

• i)    Calculate P(Play|Outlook) using step 2 of algorithm 1

P(Outlook)=P(Sunny)+P(Overcast)+P(Rainy)

=5÷14+4÷14+5÷14=1

P(Sunny|Yes)=2/9= 0.222222

P(Sunny|No)=3/5= 0.6

P(Overcast|Yes)=4/9= 0.444444

P(Rainy|Yes)=3/9= 0.333333

P(Rainy|No)=2/5=0.4

P(Outlook|Yes)=0.222222×0.444444×0.333333

=0.032917

P(Yes|Outlook)=0.032917×0.64285 =0.021164

P(Outlook|No)=0.6×0.4=0.24

P(No|Outlook)=0.24×0.357149=0.085714

P(Play|Outlook)= P(Yes|Outlook) + P(No|Outlook)

= 0.021164+0.085714 = 0.106878

• ii)    Compute I(Outlook) using step 3 of algorithm 1

I (Outlook) = log 2 (1÷0.106878)=3.225959

W outlook = 3.225959

Finding the feature weight for the feature 'Temperature' with the target 'Play':

• i)    Calculate P(Play|Temperature)

P(Temperature)=P(High)+P(Low)=6÷14+8÷14=1

P(High|Yes)=4/9=0.444444

P(High|No)=2/5=0.4

P(Low|Yes)=5/9=0.555555

P(Low|No)=3/5=0.6

P(Temperature|Yes) = 0.444444×0.555555=0.246914

P(Yes|Temperature) = 0.246914×0.642857=0.158730

P(Temperature|No) = 0.4×0.6=0.24

P(No|Temperature)=0.24×0.357142=0.085714

P(Play|Temperature)=

P(Yes|Temperature)+P(No|Temperature) = 0.158730+ 0.085714 = 0.244444

• ii)    Compute I(Temperature)

I (Temperature) = log2 (1÷0.244444) =2.032421

W Temperature = 2.032421

Similar calculations are performed for the remaining fields of weather dataset viz., Humidity and Windy. Table 4 shows the summary of the results for the weather dataset using the proposed work.

Table 4. Final Results of the Proposed Work for the Weather Dataset

F i	P(Play|F i )	WF i
Outlook	0.106878	3.225959
Temperature	0.244444	2.032421
Humidity	0.2	2.321928
Windy	0.228571	2.129283

From table 4, it is evident that the feature which has less posterior probability has more information relevant to the target and vice versa. The work assigns median of W'sas the threshold δ for each dataset and selects the features whose W is greater than δ. According to this

SF opt for weather dataset contains 'Outlook' and 'Humidity'. As median is the midpoint average of the class, the proposed method enhances the performance of NBC with limited number of selected features say approximately 50%.

V.    Experimental Results

In order to analyze the effectiveness of the proposed method, an empirical study has been performed with 6 datasets which are taken from UCI machine learning repository [12]. Each dataset comprises of both nominal and continuous features. The comprehensive description of the datasets is illustrated in Table 5. The proposed method for selecting the more relevant features has been implemented in python. The number of features selected and the selected features for each dataset is shown in Table 6 and its graphical representation is shown in Fig. 2. From Table 6, it is observed that the number of features in the optimal subset is approximately 50% from the original features because the proposed algorithm considers only the top 50% of relevant features in the original feature space. As the optimal subset contains a fewer number of features (approximately 50%) in the original which results in dimensionality reduction.

The original and the newly obtained dataset containing only the selected attributes using the proposed algorithm are fed into NBC using WEKA, for determining the predictive accuracy with 10-fold cross validation method and the results are shown in Table 7. Its corresponding graph is shown in Fig. 3. From Table 7, it is observed that the predictive accuracy of NBC for 4 datasets viz., Weather, Pima Indian Diabetes, Statlog Heart and Eeg is significantly improved for the selected features. For Ann-train dataset, the accuracy is decreased for the selected features. But for Breast Cancer, the accuracy remains the same for the original and the selected features. Thus on an average, it has been found that the accuracy of NBC is improved with the subset of selected features. The reason for this is that both BT and SI combination helps to identify the perfect features, which provide more information to the target and there is no possibility for irrelevant and least relevant features in the resultant optimal subset. Hence it is concluded that the proposed FS using BT, SI and SFS enhances the accuracy of NBC with approximately 50% of the original features and the accuracy enhancement is 1.02%.

Table 5. General Characteristics of Datasets

S. No	Data Sets	#Features			#Classes	#Instances
		Numeric	Nominal	Total
1	Weather	2	3	5	2	14
2	Breast Cancer	10	1	11	2	699
3	Pima Indian Diabetes	8	1	9	2	768
4	Statlog Heart	13	1	14	2	270
5	Ann-train	21	1	22	3	3772
6	Eeg	14	1	15	2	14979

Table 6. Comparison of Original Features and Selected Features

Datasets	Total no. of Features	No. of Features Selected	Selected Features
Weather	5	2	1,3
Breast Cancer	11	6	3,6,7,8,9,10
Pima Indian Diabetes	9	5	1,2,6,7,8
Statlog Heart	14	7	3,6,9,10,11,12,13
Ann-train	22	11	1,4,5,9,12,14,17,18,19,20,21
Eeg	15	7	1,6,7,11,12,13,14
Total (%)	76 (100%)	38 (50%)

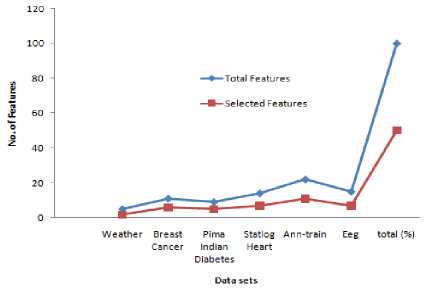
Fig.2. Original features vs. selected features

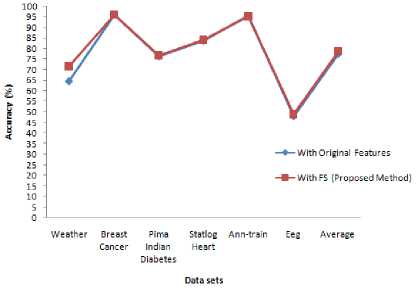
Fig.3. Accuracy comparison of NBC with original features and selected features

Table 7. Accuracy Comparison of NBC with Original Features and Selected Features

Dataset	Accuracy (%)
	With Original Features (All)	With Selected Features (Using Proposed Method)
Weather	64.2857	71.4286
Breast Cancer	95.9943	95.9943
Pima Indian Diabetes	76.3021	76.6927
Statlog Heart	83.7037	84.0741
Ann-train	95.6522	95.1485
Eeg	48.0406	48.9285
Average	77.32	78.71

Further, this work also evaluates the performance of the proposed work by determining precision and recall of NBC for each datasets using (6) and (7) and they are shown in Tables 8 and 9 respectively. The corresponding graphs are shown in Fig. 4 and 5 respectively. From Tables 8 and 9, it has been found that the weighted average of precision and recall of NBC using the selected features have been considerably increased than that of the original features.

Table 8. Precision Comparison of NBC with Original Features and Selected Features

Dataset	Precision
	With Original Features	With Selected Features (Using Proposed Method)
Weather	0.607	0.706
Breast Cancer	0.962	0.961
Pima Indian Diabetes	0.759	0.762
Statlog Heart	0.837	0.841
Ann-train	0.95	0.942
Eeg	0.529	0.537
Average	0.774	0.792

Table 9. Recall Comparison of NBC with Original Features and Selected Features

Dataset	Recall
	With Original Features	With Selected Features (Using Proposed Method)
Weather	0.643	0.714
Breast Cancer	0.96	0.96
Pima Indian Diabetes	0.763	0.767
Statlog Heart	0.837	0.841
Ann-train	0.957	0.951
Eeg	0.48	0.489
Average	0.773	0.787

As the Accuracy, Precision and Recall of NBC have been increased for the selected features using the proposed work, it is indicated that the combination of BT, SI and SFS for FS is more suitable for enhancing the performance of NBC. The main advantage of the proposed work is that the values computed for BT viz.,

P(C j ) , P(F i ) and P(F i |C j ) in the pre-processing step will be useful to reduce the time for constructing the model of NBC if they are used in the learning phase. It is evident from the literatures that the wrapper model always uses the specific learning algorithm itself to assess the quality of the selected features and it generally provides better performance than filter because the feature selection process is optimized for the particular classification algorithm to be used [13]. As the proposed work has been used to promote the accuracy of the NBC, it is recommended that the proposed framework can be used as wrapper model in future using NBC as the learning algorithm. Normally the wrapper models are very expensive than filter and filters are faster than wrappers, but if the recommended framework is used, the time and cost may be saved because BT is used both in FS and NBC.

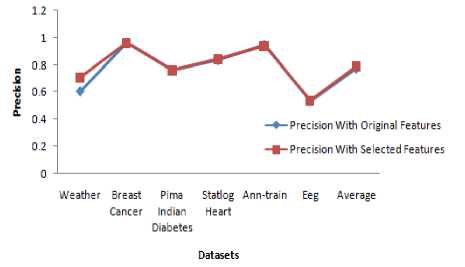
Fig.4. Precision comparision of NBC with original features and selected features

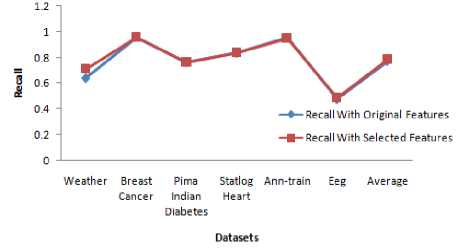
Fig.5. Recall comparision of NBC with original features and selected features

VI.    Conclusion

This paper presents a novel method of integrating BT and SI in measuring the feature weight. The weighted features are fed into SFS for selecting the strongly relevant features from the feature space. The more relevant features selected by the proposed method are fed into NBC to determine the predictive accuracy, precision and recall. From the experimental results it has been observed that the predictive accuracy of the NBC is increased approximately by 1% using the subset of features chosen by the proposed method. Similarly, the precision and recall of NBC have also been increased considerably. Further the time taken in building the model of the NBC can be reduced if the computed values of BT in the preprocessing are used in the learning phase. The other main advantage of the proposed method is that it uses MBD for discretizing the continuous features which eliminates outliers and the need to specify the number of bins.