An efficient image block encryption for key generation using non-uniform cellular automata

Image cryptography plays a momentous role in securing confidential images and are usually based on username and password. As user authentication techniques do not usually provide enough security for information enabled services, there is a need for an efficient method to protect user sensitive information, more so in a public cloud [22]. Hence, a novel TSS based image block encryption using reversible cellular automata in public cloud has been attempted in this paper. Two achievements are achieved in the proposed method that are (i) It is easy to implement in cloud storage applications and the keys strength is much better than others (ii) It provides better security with less computations.

• A.    Cloud Computing

Cloud computing is an internet based computing that virtualized, runtime accessible and the resources are delivered as a service across the web. It can be accessed anywhere, anytime and anyplace in the world over the internet. As stated in the NIST [13] description, “Cloud computing as a model for enabling ubiquitous, convenient, on-demand network access to shared pool of configurable computing resources that can be rapidly provisioned and released with minimal management effort or service provider interaction".

Cloud computing includes three typical services such as software as a service, infrastructure as a service and platform as a service and its demand can be executed as to four deployment models: private cloud, public cloud, hybrid cloud and community cloud as shown in Fig:1. Also, it includes scalability, pay-per-use, data storage, service level agreements [4, 12]. Cloud Service Provider (CSP) takes the responsibility to provides high security for customer’s secret information and compact with many services that can assist users to access their data anywhere, anytime and anyplace [17].

• B.    Celluar Automata

A cellular automata is a regular grid of cells which depends on neighborhood cells on its left, its right and the cell itself. It is reversible if it is global map is returnable [9]. In case the cellular automata is returnable which is settled in both ways is called as encryption. Hence, each rule considers as an inverse rule in the CA method. By executing CA rule in both directions such as forward and backward and then iterating for n times, the original configurations can be obtained which are explained in Table 1 and Table 2.

For example Rule 15 has an inverse to Rule 85. Cellular automata have become the significant tool in developing high speed encryption like mobile devices. One of the vital skin tones of using reversible cellular automata is the capability to create highly random generators that are appropriate for high speed applications [3] especially in the cloud environment.

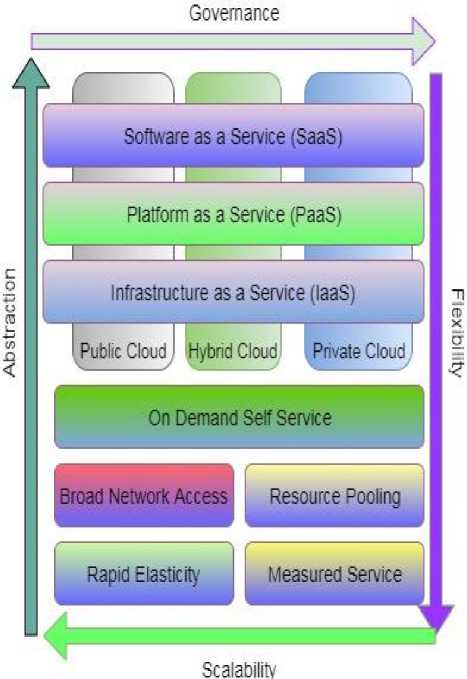
Fig.1. Cloud Computing

Table 1. Rule 15 has an inverse to Rule 85

R-15	111	110	101	100	011	010	001	000
	0	0	0	0	0	0	0	0
T	1	0	1	1	1	0	0	0
T+1	1	0	1	0	0	0	1	1
T+2	0	0	1	0	1	1	1	0
	Ta	ble 2. R	ule 85 has an in		verse	to Rule 15
R-85	111	110	101	100	011	010	001	000
	0	1	0	1	0	1	0	1
T	0	0	1	0	1	1	1	0
T+1	1	0	1	0	0	0	1	1
T+2	1	0	1	1	1	0	0	0

According to Kerckhoff's principle the secrecy of key only provides security, even though the cryptographic system is more complicated [8]. Many researchers have studied different methods and innovative approaches for key generation in public clouds [5, 16, 21]. Still, attackers prove too smart to overthrow all known security systems. The proposed image block encryption based TSS method using reversible cellular automata has been observed to provide better security and appear to be robust in cryptographic systems.

The rest of the paper is organized as follows: Section 2 introduces the literature review. In Section 3 we briefly illustrate the new TSS method, in Section 4 we provides the security analysis. In Section 5 we explain the experimental results, in Section 6 we conclude the paper.

• II.    Literature Review

In this part, we study the previous methods before presenting our proposed TSS scheme for image encryption. Recently many researchers have studied different cryptosystem approaches based on CA [1, 2]. Wolfram had presented first CA based secret key generation [20]. However, CA has the minimum number of reversible rules and inefficient to provide the long sequence of numbers [15]. To overcome these drawbacks, Sen et al. designed a stream cipher based random number generation based on CA [14]. Though, the system has increased the complexity.

To overcome this shortcoming Wang et al. introduced bit level image encryption depend on CA [18]. Also, it is vulnerable to chosen plaintext attack. Due to this disadvantages, many researchers focused on block cipher based cryptosystems in recent years. In general, the cryptographic method is used to generates random keys are remembered and the adversary can crack it. However, the proposed system to overcome these drawbacks by using a reversible CA mechanism based image key generation. Without knowing the corresponding CA transition rule, the adversary cannot obtain the original information from the proposed method as CA has undecidability in nature.

• III.    Proposed TSS Method

With an aim to strengthen user security in public cloud a novel method has been proposed. The original image (IM_n) is considered as N X N matrix at the outset. In the first step, the content owner splits the image into two non-overlapping image blocks IM_n1 and IM_n2 of sizes (N-1) X (N-1) as shown in Fig: 2(a)-(c). The diagonal pixels of IM_n are partitioned to form the 8-bit gray scale image block represented as IM_n2 and the rest is considered as IM n1 .

• A.    Key Generation Schema

A good encryption key generation algorithm has to be sensitive to the initial values of the parameters concerned and the proposed method uses the logistic function to generate the initial values for specific threshold conditions. This function covers the mask of the image IMG n2 as described below:

L n + i = r x L n (1 - L n )              (1)

In (1), the radius r and the initial value Ln are supplied as input for logistic function which reflects a chaotic behavior when 0 < Ln < 1 and 3.99 < r <4. After initiating the values for the key, the threshold function is used to store the binary values into IMGn2 with the following conditions:

(1,1)	(1,2)	(1,3)	(1,4)	(1,5)	(1,6)	(1,7)	(1	8)
(2,1)	(2,2)	(2,3)	(2,4)	(2,5)	(2,6)	(2,7)	(2	8)
(3,1)	(3,2)	(3,3)	(3,4)	(3,5)	(3,6)	(3,7)	(3	8)
(4,1)	(4,2)	(4,3)	(4,4)	(4,5)	(4,6)	(4,7)	(4	8)
(5,1)	(5,2)	(5,3)	(5,4)	(5,5)	(5,6)	(5,7)	(5	8)
(6,1)	(6,2)	(6,3)	(6,4)	(6,5)	(6,6)	(6,7)	(6	8)
(7,1)	(7,2)	(7,3)	(7,4)	(7,5)	(7,6)	(7,7)	(7	8)
	*		-tw-	-fw-	■w	W	-#	«Г

(1,1)	(1,2)	(1,3)	(1,4)	(1,5)	(1,6)	(1,7)
(2,1)	(2,2)	(2,3)	(2,4)	(2,5)	(2,6)	(2,7)
(3,1)	(3,2)	(3,3)	(3,4)	(3,5)	(3,6)	(3,7)
(4,1)	(4,2)	(4,3)	(4,4)	(4,5)	(4,6)	(4,7)
(5,1)	(5,2)	(5,3)	(5,4)	(5,5)	(5,6)	(5,7)
(6,1)	(6,2)	(6,3)	(6,4)	(6,5)	(6,6)	(6,7)
(7,D	(7,2)	(7,3)	(7 4)	(7,5)	(7.6)	(7,7)

(b)

(a}

(1,8)	(2,8)	(3,8)	(4,8)	(5,8)	(6,8)	(7,8)	(8,8)
(8,1)	(8,2)	(8,3)	(8,4)	(8,5)	(8,6)	(8,7)	(8,8)

(c)

Fig.2. Partition of image block (a) Original image IMG n , (b) User’s plaintext image IMG n1 , (c) Cellular automata rule image IMG n2

f ( L n ) =

1,    L n >  0.5

0, L n <  0.5

Cellular automata (CA) is a regular grid of cells, which depends on its neighbors to the left, neighbors to the right and cells itself. The major drawbacks of CA in cryptography along with the minimum number of reversible rules and failure to produce the long sequence of numbers. To overcome these drawbacks, we use eight best CA rules (i.e., R153, R86, R101, R30, R105, R90, R165, R150) in the proposed TSS method which have the best results such as entropy [20].

First, we choose the eight best selected CA rules with 2³ blocks in IMG_n2. Consequently, each block will contain different CA rules in IMG_n2. For example, let us take a block from IMG_n2. Suppose the block contains rule30, then the key length will be 128 bits. Then, before ciphering the text in IMG_n, we need to generate a master key in IMG n2 . Usually, the traditional techniques used for generating the master key suffer from various attacks such as chosen plain text attack, statistical cryptanalysis and brute force attacks. Therefore, the TSS method to generate the required master key using IMG_n2 which is robust to mitigate these attacks has been proposed in this paper.

The proposed model contains three stages: user (U i ), cloud service provider (CSP i ) and cloud service provider machine (CSPM i ). After initiating the values, a CA rule from IMG n2 block will be selected using SL i = | L n X 7|+1. The value of L_n can be obtained from logistic functions. In the first stage, U_i needs to select a CA rule from IMG_n2 denoted as K_a1. In the second stage, CSPM_i selects a CA rule K_a2 from IMG_n2. Both K_a1 and K_a2 are added. The resulting value K_a12 is temporarily stored in a memory buffer. In the third stage, CSP_i selects another CA rule K a4 from IMG n2 block and it is added with previously result K a12 . Finally, it is the robust master key K a124 in the form of binary values. The detailed process of the generation of master key is illustrated as shown in Fig:3.

• B.    Block Encryption

After generating K a124 , the IMG n1 block is XORed with IMG_n2 block. Then, IMG_n1 contains U_i's plaintext (PT_i) information in the form of binary values. The result will be produced at the end of the encrypted block IMG_n3.

Finally, the IMGn3 will be sent to the registered Ui's via smart phone. If Ui enters the correct code, then they can access the cloud services, otherwise the request will be denied.

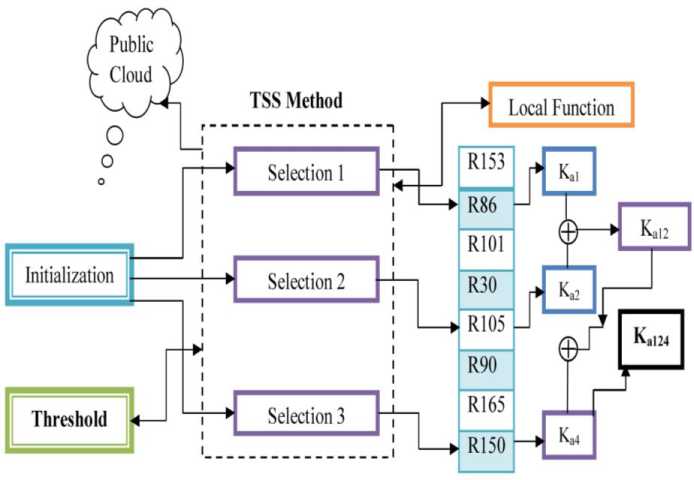
Fig.3. Detailed Process of Generating Image Key

• IV.    Security Analysis

• Theorem 1:    The proposed method is correct in verifying the correctness of computation results.

Proof: From section 3, let us consider the following logistic map function:

L n + i = r x L n (1 - L n )

with the interval from when 0 <  L n < 1 and 3.99 <  r <4. Where r represents radius. After satisfying interval, we can choose the binary values based on the following conditions:

For f (L) > 0.5 , then stored 0 and f (L) < 0.5 , then stored 1 in the matrix.

That is,

к

N x N

0.232	0.243	0.632	••  x1 n
0.372	0.285	0.821	X 2 n
0.328	0.234	0.366	" X 3 n
xd 1	xd 2	xd 3	x dn _

Hence, each number is used to encrypt each pixel in the matrix. Therefore,

	"0.232	0.243	0.632	••  X 1 n "
	0.372	0.285	0.821	x 2 n
K N x N =	0.328	0.234	0.366	x 3 n	x 255
	........... _ x d 1	xd 2	xd 3	....... x dn _

So, we have the following matrix

	"59	62	161	X'n 1
	95	73	209	" X 2 n
K N x N =	84 .	60	93	■■  X 3 n
	_ xd 1	xd 2	xd 3	'    xdn _

Then, the obtained matrix converted into 8-bit binary number and it becomes:

K N x N

xd1           xd2           xd3

Hence, the proposed method takes first 8-bit number of K NXN as input of the cellular automata selected rules from SL i . Now assuming,

CA = 0 0 1 1 1 0 11

In case the first stage, the U i selects Rule30 from IMG n2 , we obtained:

Rule30 binary expression: U t⁺¹ = U^xor _ U t orU t₊ ^

0   0   1   1   1   0   11

CA'= 11101011(3)

where CA' represents first stage first iteration state result.

1    1    1   0   1   0   11

CA''= 00100010                (4)

where CA'' represents first stage second iteration state result. Then, equation (3) added with equation (4) and it becomes:

11101011 + 00100010 = 100001101

Therefore, the first stage result is: 100001101

Similarly in the second stage, the CSPMi selects Rule153 from IMGn2 and it becomes:

Rule153 binary expression: U t+1 = U t xnor ^ U ^ ^

1   0  0  0  0   1   1   01

CA'= 01110100(5)

where CA' represents second stage first iteration state result.

0   1   1   1   0   1   00

CA''= 01100011(6)

where CA'' represents second stage second iteration state result. Then, equation (5) added with equation (6) and it becomes:

01110100 + 01100011 = 11010111

Therefore, the second stage result is: 11010111

Similarly in the third stage, the CSP i selects Rule165 from IMG n2 and it becomes:

Rule165 binary expression: U t⁺¹ = Utxnor ^ U ^ ^

1   1   0   1   0   1   11

CA'= 10111011(7)

where CA' represents third stage first iteration state result.

1   0   1    1    1   0   11

CA''= 01010101(8)

where CA'' represents third stage second iteration state result. Then, equation (7) added with equation (8) and it becomes:

10111011 + 01010101 = 100010000(9)

Therefore, the third stage result is: 100010000

Therefore, the image key values is: 272

Similarly, to perform a decryption process. Hence, the proposed method uses the same rules (i.e., Rule30, Rule153, Rule165) while decrypting the final image key. In the end, it obtained the initial key 59 (i.e., 00111011). The system remembers all the selected rules while encrypting the initial key image.

It is proved that the proposed method computation result is correct in the system.

• Theorem 2:    The proposed method supports the robustness of the key image against cipher plaintext attack.

Proof: According to the recent proposal on IMG n the block enciphering schema, the master key should meet all the basic security requirements such as avalanche criteria (AVL c ), confusion (CFS p ) and diffusion (DFS p ) properties. The criteria AVL c is evident when an input changes slightly and the output changes dramatically. Such a small change in the K_a124 and PT_i which has to cause a significant change in CT_i.

The TSS method meets these criteria by using a logistic function L_n+1 from (1) to generate the initial parameter values for a key generation. CFS p is about the relationship between CT i and K a124 which has to be as much complex as possible and this is achieved through CFS p with three stages and the selected key values K a1 , K a2 and K a4 from IMG n2 block and thus, the computations leads to generate a enough complexity.

Hence, it provides better K_a124. DFS_p is about the relationship between PT_i and CT_i which has to be as much complex as possible and this is achieved through DFS_p with both L_n+1 and K_a124 techniques. Therefore, the TSS method meets all the basic security requirements of image block encryption and also prevents the chosen plaintext attack in public cloud.

• A.    Key Space Analysis

  An encryption scheme has to be sensitive to all the encryption keys. Based on U i 's requirements, a key K a124 of 128-bit length (with a possibility of choosing 2¹²⁸ keys) is generated. Here, L n+1 from (1) is used as the key initiator and the images IMG_n3 of sizes N X N used for encryption that results in 2^{8X NXN} choices. These are clearly sufficient to prevent all possible attacks.

• B.    Efficiency

From Theorem 1, the proposed method executed with a low computational cost. It is noticed that many functions are assigned to the cloud environment. Hence, the U i 's needs to generate keys after the data stored in the cloud. Also, the system input is independent of the proposed system efficiency.

• V.    Experimental Results

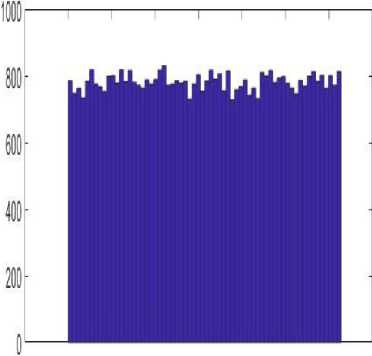
In our experiment, the different statistical tests and measurements are implemented with three gray scale (512 X 512) images such as Lena, Baboon and Peppers from [6]. Fig: 4(a) shows the original lena gray scale key image. Fig: 4(b) shows the encrypted lena key image using proposed TSS encryption algorithm. Also, Fig: 4(c) shows the decrypted lena key image which is similar to the Fig: 4(a). Our method meets the requirements on the histogram (HGM) and data entropy (ENV n ). HGM has to be fall on a uniform distribution of the pixel values. Figure 5 shows that the HGM analysis of the IMG n3 images is uniform way. Therefore, without the knowledge of K_a124 values, there is no possibility of statistical attacks and the adversary cannot steal any information about the

PT i block of IMG n1 .

Also, the ENV_n is concerned with randomness test. High ENV n indicate a high degree of randomness in values for any message that is coded into n bits, as the gray level images are coded into 8 bits and the optimal ENV n is 8. The ENV n is calculated using (10).

(a)                        (b)

(c)

Fig.4. Test image: Lena (a) The original key image (b) The encrypted key image (c) The decrypted key image

prevent statistical cryptanalysis attack. Also, the adversary cannot extract the required information from IMG n1 without the knowledge of K a124 value.

Table 3. Entropy Value of Plain and Proposed Images for TSS and Existing Methods

Images	Plain	Proposed	[19]	[7]
Lena	7.3401	7.9988	7.9926	7.9986
Baboon	7.1125	7.9975	7.9934	7.9920
Peppers	7.0725	7.9988	7.9923	7.9987

Table 4. Illustration of Key Generation Time (sec)

Entry	[11]	[10]	Proposed
19	13.9	15.1	5.5
14	9.0	10.5	4.1
10	8.7	9.9	4.0
6	3.7	5.8	2.4
2	2.6	4.4	1.0

The key generation time has been examined based on number records in the CSP database. It has been found that the proposed method has better results in comparison with existing methods in [10, 11]. Also, in case the number of entries increased the key generation time is decreased this is shown in Table 4 and graphically shown in Fig: 6.

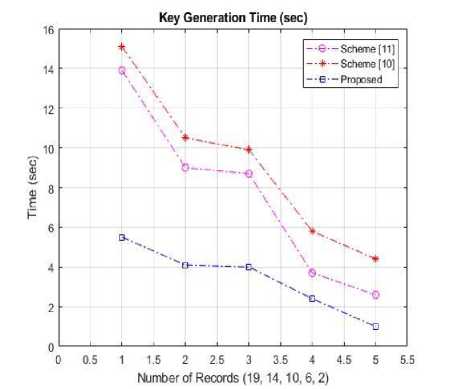
Fig.6. Analysis of Key Generation Time

■10 3 2 3)567

Fig.5. Lena Histogram Key Image

2 N -1

H ( m ) = - £ P c log₂( P c )           (10)

c=0

where P c represents different gray scale image values from 0 to 255.

Hence, Table 3 interprets the different ENV_n which are obtained from IMG n and IMG n3 . The results are compared with existing two block based methods proposed in [7, 19]. It has been found that the IMG n3 has achieves near optimal ENV n which is sufficient to

• VI.    Conclusions

  A novel image block encryption for key generation using TSS method with reversible cellular automata to secure highly sensitive data in the public cloud has been proposed and analyzed in this paper. The encrypted key prevents the statistical cryptanalysis attacks and brute force attack and as it also satisfies the avalanche criterion, confusion and diffusion properties, chosen plain text attack is prevented. Finally, the results obtained show that the proposed method provides better performance and an enhanced ciphered image entropy value of 7.9988 which an ideal one for any image block encryption method for key generation.

Acknowledgment

This work has been supported by the University Grants Commission in India under rajiv gandhi national fellowship (Reference number: F1-17.1/201516/RGNF-2015-17-SC-TAM-4667).