An efficient indexing technique for AES lookup table to prevent side-channel cache timing attack

Published Online September 2018 in MECS DOI: 10.5815/ijcnis.2018.09.03

• I.    Introduction

  Out of the five candidate algorithms (MARS [1], RC6, Rijndael [2], Serpent [3], and Twofish [4]) for the AES model, Rijndael was pronounced as a new standard on November 26, 2001 as FIPS PUB 197 [5]. The security barrier of Rijndael cipher is so strong that a cryptographic break is infeasible with current technology. Even Bruce Schneier, a developer of the competing algorithm Twofish, admired Rijndael cipher in his writing, “I do not believe that anyone will ever discover an attack that will allow someone to read Rijndael traffic” [6].

A brute force method would require 2128 operations for the full recovery of an AES-128 key. A machine that can perform 8.2 quadrillion calculations per second will take 1.3 quadrillion years to recover this key. Nevertheless, partial information leaked by side-channels can tear down this complexity to a very reasonable level. Side-channel attacks do not attack the underlying cipher; instead, they attack implementations of the cipher on systems that inadvertently leak data. Ongoing research in the last decade has shown that the information transmitted via side-channels, such as execution time [7], computational faults [8], power consumption [9] and electromagnetic emissions [10, 11, 12], can be detrimental to the security of Rijndael [13] and other popular ciphers like RSA [14].

In this paper, we will be primarily focusing on the vulnerability of Rijndael AES to side-channel cachetiming attack and see how simple cache misses in a multiprogramming environment can lead to disastrous consequences. If the plaintext is known, recovery of half of the key by any privileged process is a matter of seconds. The prevention is not trivial; there exists tradeoff between performance and degree of multiprogramming. We will present a concept that balance this trade-off by introducing a little memory overhead. It is worth mentioning that even though the process is arbitrary, the cipher text will always remain the same.

• II.    Related LiteraTURE

  In October 2005, Dag Arne Osvik, Adi Shamir and Eran Tromer presented a paper demonstrating several cache-timing attacks against AES [15]. One attack was able to obtain an entire AES key after only 800 operations triggering encryptions, in a total of 65 milliseconds. The attack required the attacker to be able to run programs on the same system or platform that is performing AES. That paper presented some decent defense against side-channel cache-timing attacks such as avoiding memory access, disabling cache sharing, 30

dynamic table storage etc. They revised their paper on 2010 [16] and focused on modern microprocessor implementations and presented few more preventions. Most of them lacked conceptual consolidation and provided as implicit implication. Some of them even requires alteration of cipher text that might cause significant overhead in distributed systems to maintain synchronization. Other works included introduction of asynchronous circuitry in AES implementation [7].

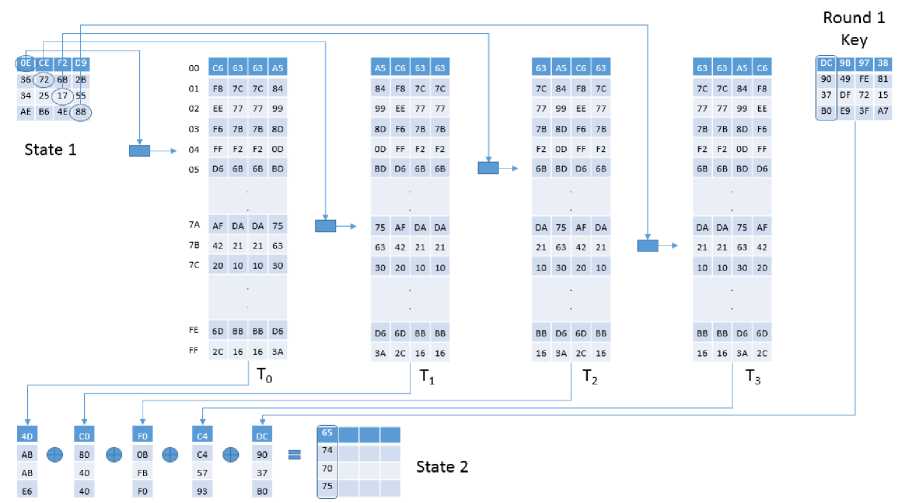
00 У 01 FB 7C 7C 84

State 1

84 F8 7C 7C

7C 84 F8 7C

7C 7C 84 F8

Round 1 Key QgQjQQ

State 2

Fig.1. The Figure Demonstrates how x 1 , x 1 , x 1 , x 1 are Computed. Note that the Bytes of the State Matrix are being used as index of the Lookup Tables. Since the Lookup Table Remains the same for a Particular S-Box, An Index byte will always Cause Lookup from the same block of Cache Memory.

(xor+1), x(r+1),x(r+1),x(r+1)) ^ To[xo(r)] ф T1[xs(r)] ф T2[x1o(r)] ф T3[x15(r)] ф Ko(r+1) (xor+1),xp”+1),x2r+1),x3r+1)) ^ To[xo (r)] Ф TJx5 (r)] ф T2[xw(r)] ф T A /. (r)] ф <+1)

(x4"+1),x5r+1), x6r+1),x7r+1)) ^ To[x4(r)] ф Т1 [x9(r)] ф Т2 [x14(r)] ф T3 [x3(r)] ф <+1)          (1)

(x8r+1),x,r+1),x(o+1),x(1+1)) ^ To[x8(r)] ф T1[x13(r)] ф T2[x2(r)] ф TgfotoJ ф ^o(r+1) (x^x^+^x^x^ ^ To[x12(r)] ф T1[x1(r)] ф T2[x6(r)J ф T3[x11(r)] ф <+1)

Before understanding the weakest part of the cipher, we are going to clarify the concept of cache memory and how they are accessed during real time AES implementation in the remainder of this section.

• A.    Memory Access in AES Implementations

The memory access patterns of AES are particularly susceptible to cryptanalysis. The cipher is abstractly defined by algebraic operations and could, in principle, be directly implemented using just logical and arithmetic operations. However, performance-oriented software implementations on 32-bit (or higher) processors typically use an alternative formulation based on lookup tables as prescribed in the Rijndael Specification [13]. A number of lookup tables are precomputed once by the programmer or during system initialization. Here, there are 8 such tables, To,T1, T2,T3 and To,T1,T2,T3 , each containing 256 4-byte words. The contents of the tables, defined in [13], are inconsequential to most of the cachetiming attacks because of memory protection.

During key setup, a given 16-byte secret key к = (k₀, k 1 , ..., k₁₅) is expanded into 10 round keys, K^(r^ or r = 1, 2,..., 10. Each of these rounds is divided into 4 words of 4 bytes each: K ^(r) = (K₀ ^(r) ,K₁ ^(r) ,K₂ ^(r) ,K₃ ^(r) ). The 0 ^th round key is just the raw key: K^(o = (к 4] ,к 4]+1 ,к 4]+2 ,к 4]+3) for j = 0,1, 2, 3. The details of the rest of the key expansions are mostly inconsequential [16].

Given a 16-byte plaintext p = (p_o,p 1 , ... ,p₁₅), encryption proceeds by computing a 16-byte intermediate state x ^(r) = (x ^(r) , x ^(r) ,..., x^ ) ) at each round r. The initial state x ^(o) is computed by x ^(o) = Р / ф к / ([ = 0,1,...,15). Thus, the first 9 rounds are computed by updating the intermediate state as Equation 1, for r = 0,1,..., 8.

Round 1

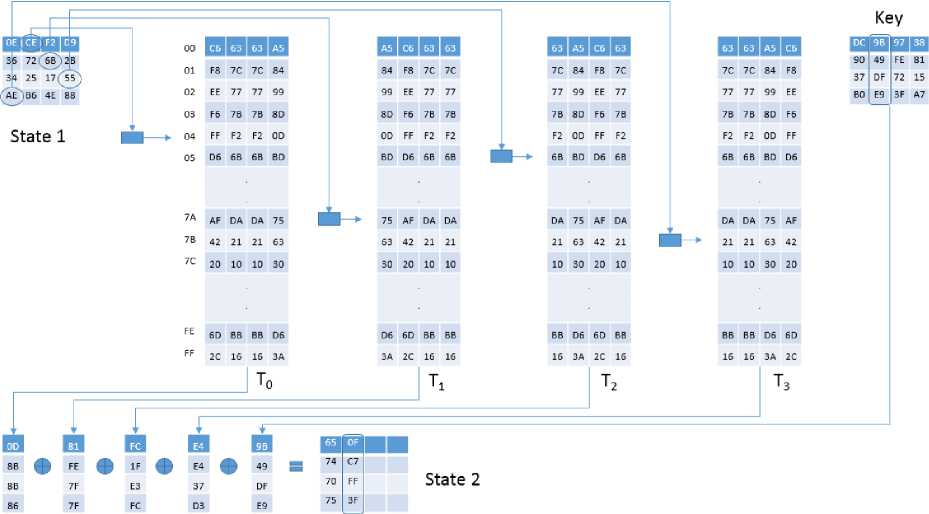
Fig.2. The Figure Demonstrates how x 1 , x j , x 1 , x¹ are Computed.

Finally, to compute the last round, the above process of table lookup is repeated with r = 9, except that

T ₀ , T 1 , T₂, T ₃ are replaced by T_o ⁽¹⁰⁰ , T^ ¹⁰ ) , T₂ ⁽¹⁰⁰ , T₃ ⁽¹⁰⁰ . The resulting x ⁽¹⁰⁰ is the cipher text. Compared to the algebraic formulation of AES, here the lookup tables represent the combination of ShiftRows, MixColumns and SubBytes operations; the change of lookup tables in the last round is due to the absence of MixColumns [16]. It is clear from the above discussion that computation of a state matrix requires 16 Table lookups and 16 XOR operations.

We know, the first round state matrix is computed by XOR operation between the 16-byte plain text and the 16-byte plain key. One important point to notice from the previous discussion is that the state bytes are being used as index to the lookup tables. Thus any Information of the accessed index will directly translate to Encryption Key Byte. For example, assume we know x ⁽⁰⁰ . Since plaintext is known for triggered encryptions, we know x ⁽⁰⁰ too (Equation 2).

x(00 ^ x(00 ф k(00                 (2)

This implies - k(00 ^ x(00 ф x(10               (3)

Thus knowing x1(10 for i = 0,1,2,..., 15 is sufficient to recover the full encryption key under the assumption that the plaintext is known. This is the weakest part of Round 1; in fact, the weakest part of the Cipher.

• B.    How Lookup Tables fit in Memory and Cache

  Having discussed the issue of memory access in AES implementation, we now turn our focus on how AES Lookup tables fit in Memory and in Cache. We know, each Lookup table has 256 4-Byte entry. That gives it a total size of 256 * 4 = 1024 Bytes. Now, typical size of memory block is 64 Bytes even on modern microprocessors. Hence, for simplicity, we will assume the memory block size B to be 64 Bytes throughout this paper. Therefore, each table T - will occupy 16 memory blocks. Also assume that, the initial address of T - congruent to the cache. That is, 1st block of the table will be cached in one of the W cache lines in the 1st cache set.

• III.    The Idealized Prime+Probe Technique

The Prime+Probe technique helps to visualize the vulnerability of AES Cipher during the 1st Round. To keep things simple, we consider an idealized environment in which only the attacking process and the victim encrypting process exists. Also assume that the attacking process will be able to invoke or interrupt the encrypting process at any time. Now since we are talking about triggered encryption, the plaintext is also known. The Prime+Probe technique has the following 3 phases: Prime, Trigger and Probe.

w

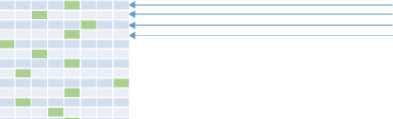
Size of a Table

S            ■   =256x4 Bytes

= 1024 Bytes

= 16 Blocks

□< В

Cache

Example Scenario,

S=32; W=8; B=64 Bytes

Total Cache Size = 32 x S x 64 Byte = 16 KB

Memory

Memory is addressed column-wise.

Fig.3. Demonstration of how AES Lookup Table fits in Memory and cache. On the Left Side, Number of Rows Implies total Number of Cache Sets, Whereas, Number of Columns Implies Associativity of the Cache. On the right side, Instead of Depicting Memory as a Continuous Array of blocks, it is Portrayed in Congruence with Cache Memory. Note that all blocks in a row of Memory Competes for the blocks of Corresponding row in Cache Memory.

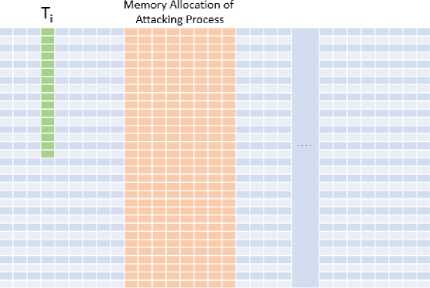
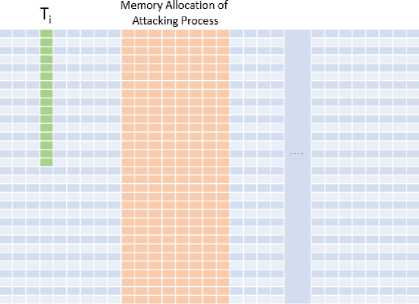
Prime: During the Prime phase, the cache is filled completely by the attacking process. This can be done by allocating a contiguous amount of memory as big as the size of the cache and performing a read on it. If S = 32, W = 8 and B = 64 Bytes, then –

Total size of the cache = S -W ■ В = 16 (4)

As implied by Fig. 3, performing a serial read on a contiguous memory as big as the cache results in inception of filling the cache. Continuing this way, we will end up filling the cache completely after the reading is finished.

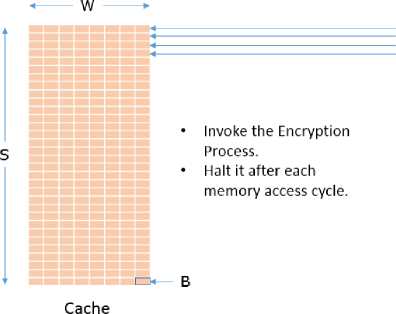
Trigger: With the Cache filled with our data, we are in a position to invoke the encrypting process and trigger an encryption of some known plain text. As the encrypting process reaches the First Round and performs the first lookup, it is interrupted. It is worth noting here that we are idealizing the model to illustrate the susceptibility of the First Round, and recovering the AES Encryption Key is not the actual intention of the contribution presented in this paper.

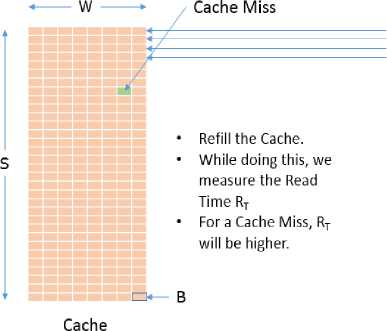
Probe: After we interrupt the encrypting process just after it performed its first lookup during the First Round of AES, we perform the Prime again; that is, we fill the cache again. However, in this time, we maintain a clock to take the measurement of how long it takes to read a memory block. Before the Trigger phase, the cache was completely filled by our data. But after that phase, one block of the Lookup table T ₀ is now in the cache due to the lookup operation. Therefore, all but that block will suffer from a cache miss.

Observing the position of the cache miss, we can easily identify which block of T₀ was accessed since we assumed

Lookup Tables T, to be congruent with the cache. Now, if we can identify which block of T0 was accessed during the First Round, we can extract some valuable piece of information. Since size of memory block is 64 Bytes, each memory block holds 16 entry of the Lookup Table. So for example, if 7th block of T0 was accessed, we can conclude the index x(1) was somewhat between 0x60 and 0x6F; that is, high nibble is 0x6. We know - xO1 = x0° Ф k00)               (5)

Here, x(0) is the 1st Byte of the plaintext and k(0) is the 1st Byte of the Encryption Key. Now, since addition and subtraction in Galois Field are the same XOR operation, rearranging the equation yields - k00) = x00) Ф x01)                (6)

Because we know x ⁽⁰⁾ from the plain text and the high nibble of x ⁽¹⁾ from the Prime+Probe technique, we can compute the high nibble of the first Byte of the Encryption Key by a simple XOR operation. Proceeding this way for every Bytes x ⁽¹⁾ for i = 0,1,2,..., 15, we can calculate k ⁽⁰⁾ for i = 0,1, 2,..., 15 and dig up half of the Encryption Key. The idealized procedure is summarized in Algorithm 1.

Memory Allocation of Attacking Process

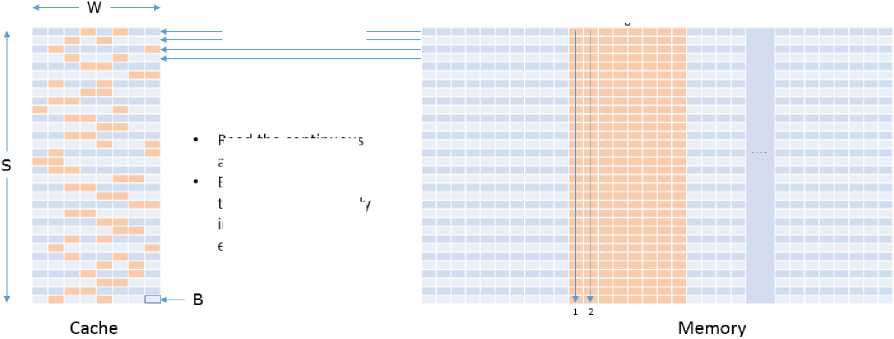
Read the continuous array of memory. Eventually it will fill the Cache completely in a noise free environment.

Example Scenario, 5=32; W=8; B=64 Bytes

Total Cache Size = 32 x 8 x 64 Byte = 16 KB

Memory is addressed column-wise.

Example Scenario,

S=32; W=8; B=64 Bytes

Total Cache Size = 32 x 8 x 64 Byte = 16 KB

Fig.4. Demonstration of the Cache Filling Process. Note that Reading Continuous Array of Memory will Cause Allocation of one block from each Cache set and due to Principle of Locality, Immediate next read Cycle will Cause Allocation of Another block (Different from the Previous) from each Cache set.

Memory

Assumptions:

• 1.    Starting Address of T, is known.

• 2.    Cache Line Size = 64 Bytes

• Fig.5.    Demonstration of the Prime phase where Reading a Continuous Array of Memory Equal to the size of the Cache will eventually fill the Cache Completely with Attacker's data in a Noiseless Environment.

• IV. Proposed Random Address Translator (RAT)

From the analysis in the previous sections, it is prominent that the existence of linear correlation between index Bytes of the state matrix and the location of corresponding accessed block in memory is the primary reason of vulnerability of AES in the first round. Given size of memory block (64 Bytes in most of the cases), any information about the memory access during the encryption process would directly reveal high nibble of the index Bytes. Thus if the size of the key is 128 Bit, pre-knowledge of the high nibbles of the index Bytes would reduce the brute force complexity to 264. A machine that can perform 1 quadrillion operations per seconds would take less than 5 seconds to break the rest of the key in brute force attempt.

Now, if the correlation can be broken, so that the index Byte will no longer be used directly to locate the desired block of the Lookup table, most of the cache-timing threats will be eliminated. The key concept to the solution is to perform memory access to obtain the desired content but from an arbitrary, unpredictable location. This can be accomplished by introducing a Translator table between the state matrix and the lookup table. The index Bytes of the state matrix will then be used as index to the Translator table to get the location of the desired block.

The Translator table is initially aligned with the Lookup table as illustrated in Fig. 7. This implies that if the address of i -th row in the lookup table is X i , the content of the i -th row of the Translator table is also X_i . Initially, it has no effect on the accessed memory block of the lookup table because it is fully aligned with it. After that, let’s take two rows of the Translator table T i and T j and corresponding two rows of the original lookup table L i and L j and perform a swap between them. This is illustrated in Fig. 8.

Continuing this way, there can be at most 128 swaps between the entries of the table. Note that an entry can be swapped only once, so keeping trace of swapped entries is important. After scrambling, the correlation is completely broken as illustrated in Fig. 9.

With the RAT activated, there is no such phrase such as, index 0x05 will access the 1st block of the Lookup table. Because the content of the address 0x05 is now at 0x7B address (Fig. 9) and that tracing is recorded by the RAT. The procedure for constructing the RAT is formulated in Algorithm 2 and 3.

After that, a scrambling is done on both tables simultaneously and arbitrarily. Note that no entry is allowed to be scrambled or swapped with other entry more than once. Also note the presence of rand() methods. It symbolizes the randomness of the swapping process.

Example Scenario,

S=32; W=8; B=64 Bytes

Iota Cache Size = 32 x 8 x 64 Byte = 16 KB

Memory

Memory is addressed column-wise.

• Fig.6.    Demonstration of how Information about the Location of the cache miss During First Round Reveals Critical Information about the Encryption Key. In the Example Scenario, the High Nibble of a Byte (0x6) is Easily Gleaned.

Algorithm 1 Abstract procedure for recovering half of the Key during the First Pound

• 1:    TriggerTheEncryption();

• 2:    for i = 0 to 15 do

• 3:    FillCache():

• 4:    HaltEncryption()

• 5:   j = MissedBlockIndex();

• 6:    j = j ^ 4;

• 8:    end for

Algorithm 2 Initializing the BAT

1:    for i e- 0x00 to OxFF do 2:    B AT[i] <- i; 3:    Swapped[i] e- false; 4:    end for

Random Address Translator

Lookup Table

00	00  -------------------------------------------► 00 C6 63 63 AS
01	01  ---► 01 F8 7C 7C 84
02	02  --------- ------------------- --------► 02 EE 77 П 99
03	03 -------------------------------------------► 03 F6 7B 7B 8D
04	04 ________► Q4 FF F2 F2 0D
05	05  ________► 05 D6 6B 6B BD

7A	7A ____► уд AF DA DA 75
7B	7B ____ ► 7 g 42 21 21 63
7C	7C-- ► 7Q 20 10 10 30

FE	FE___^ рр 6D BB BB D6
FF	FF ____pp 2C 16 16 ЗА

Fig.7. Random Address Translator Initialization.

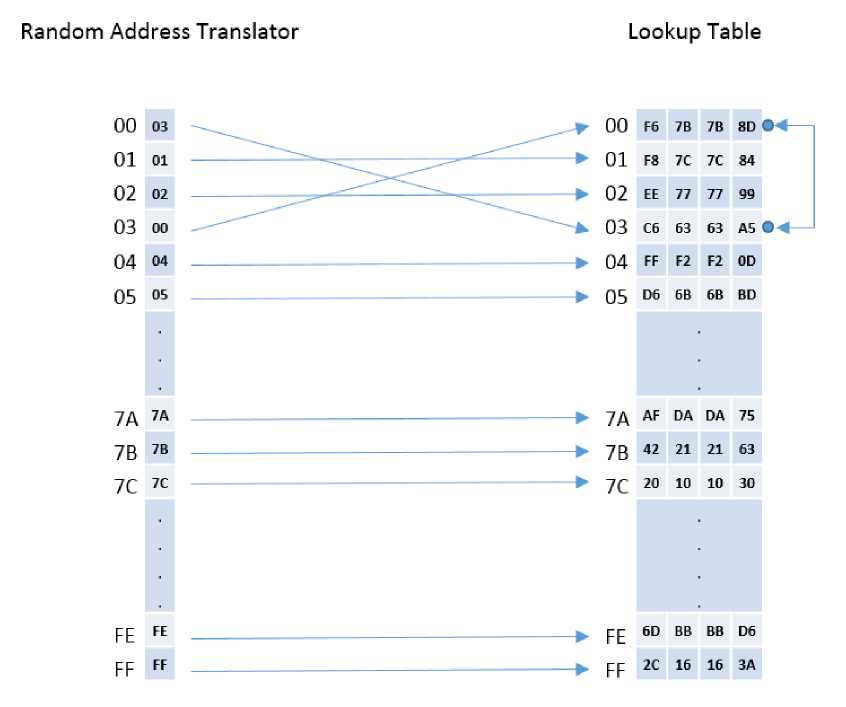
Fig.8. Random Address Translator after First Swap.

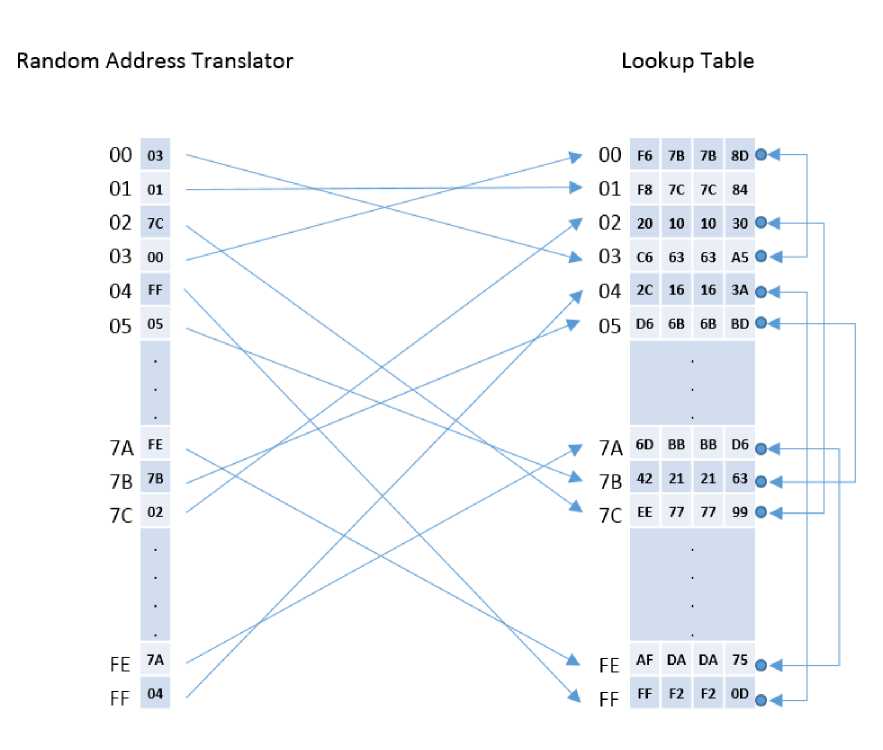
Fig.9. Random Address Translator Completely Scrambled. It can be noticed that some of the Entries can be left “unswapped” as the Process Is Arbitrary. Here 2nd Entry Is Left Intact.

Algorithm 3 Constructing the RAT

• 1:    for i e- 0x00 to 0x7F do

• 2:    in e- rand() mod OxFF;

• 3:    while Swapped[m] = true do

• 4:     in e- rand() mod OxFF;

• 5:   end while

• 6:    n e- rand() mod OxFF;

• 7:    while Swapped[n] = true do

• 8:     n ■(— randQ mod OxFF:

• 9:   end while

• 10:    swap(R AT[m],RAT[n]);

• 11:    for j •(— 0 to 3 do

• 12:      swap(T,-[m],Tj[n]):

• 13:       swap(T-^io^ [m] ,T- ¹⁰⁵ [n]);

• 14:   end for

• 15:    end for

• V. Performance Evaluation

There are some other proposed solutions in this field [16, 17, 18, 19, 20, 21, 22]. We take some of the most prominent ones and compare it with our proposed solution.

Avoiding Memory Access. Since the cache-timing attacks exploit the effect of memory access on the cache, any implementation that does not perform any table lookup will not suffer from this sort of attacks. Nevertheless, this solution has a major drawback. That is the performance is degraded by an order of magnitude. The Sub-Bytes Transformation phase requires 16 table lookups for the 16 Bytes of a State matrix. The ShiftRows Transformation phase requires 16 shift operations. The MixColumns Transformation phase requires 8 shift operations, 8 conditional XOR operations and 12 mandatory XOR operations. At the end, the AddRoundKey Transformation phase requires 16 XOR operations. To summarize the fact, we need a total of 24 shift operations, 16 table lookups, 8 conditional XOR operations, 28 mandatory XOR operations for a single round, as demonstrated in Fig.10.

■ Table Lookup ■ Shift Operation ■ Conditional XOR ■ Mandatory XOR

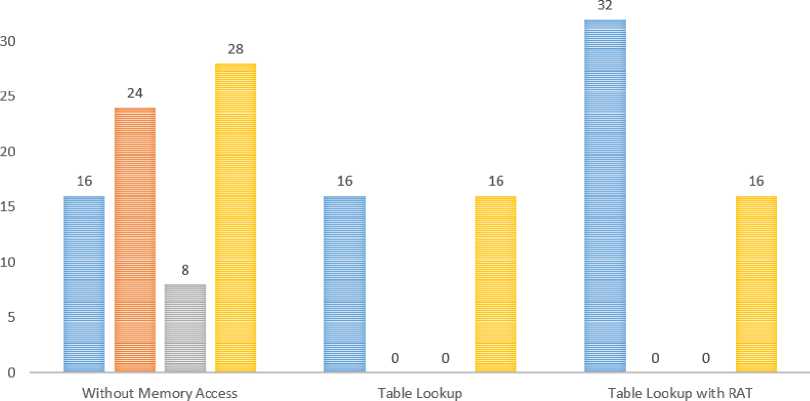
Fig.10. Comparison of RAT with Straightforward AES Implementations in a Single Round. An Implementation that Completely Avoids Memory Access Requires 16 table Lookups, 24 Shift Operations and 36 XOR Operations (8 of which them are Conditional), Whereas Introduction of RAT Incurs 2 times more table Lookups and 16 XOR Operations in a Single Round.

■ S-Box ■ Lookup Table iRATTable

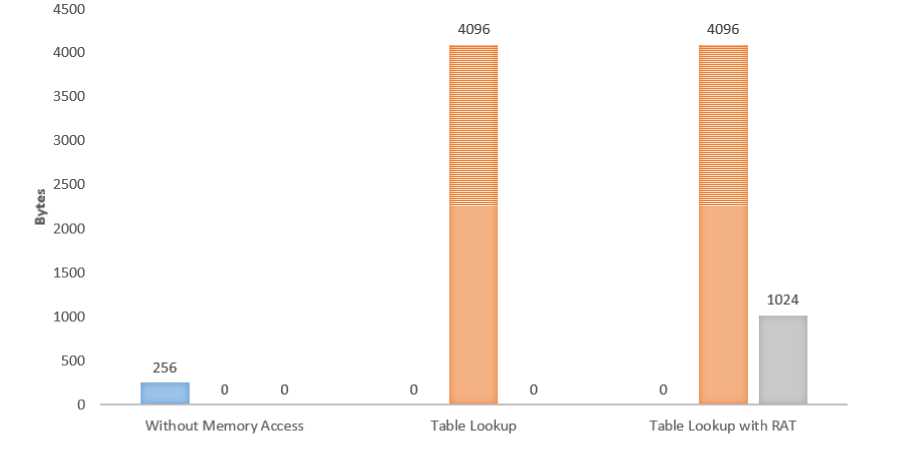
Fig.11. Performance Evaluation of RAT in terms of Memory Usage.

In fact, the conditional XOR operation is also vulnerable to timing attack [23]. Other than lagging behind in terms of security, a straightforward implementation requires more computation time. So avoiding memory access does not solve the problem. Having said that, the positive side is that the straightforward implementation does not need to maintain any sort of lookup table other than the S-Box. On the other hand, table lookup with RAT has an overhead of maintaining two tables. The Lookup table requires 4096 Bytes of memory space and RAT requires another 1024 Bytes of space.

Disable Cache Sharing. To protect against software- based attacks, it would suffice to prevent cache state effects from spanning process boundaries. However, this is very expensive to achieve in practical settings. On a single threaded processor, it would require flushing all caches during every context switch. On a processor with simultaneous multi-threading, it would also require the logical processors to use separate logical caches, statically allocated within the physical cache; some modern processors do not support such a mode [16]. Using RAT will not impose any restriction about cache sharing which is perfectly suitable for cloud environment and virtual machines (without causing evictions and filling).

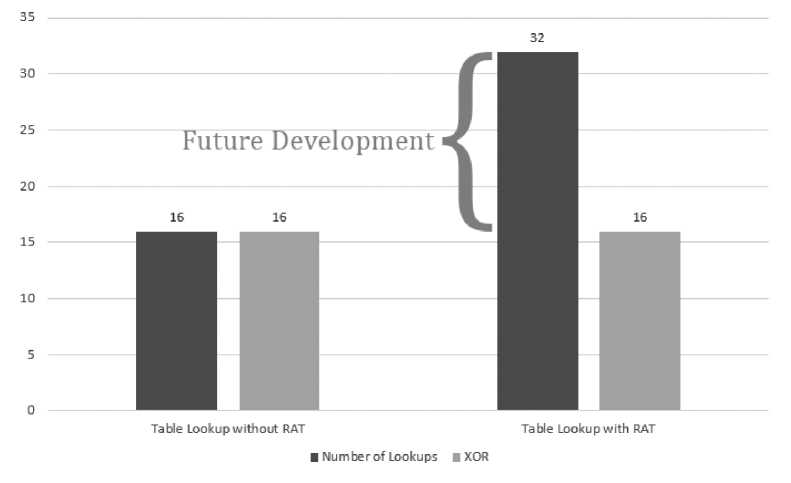
Fig.12. Comparison with Straightforward Table Lookup Approach.

Static or Disabled Cache . One brutal countermeasure against the cache-base attacks is to completely disable the CPU’s caching mechanism. Of course, the effect on performance would be devastating. A more attractive alternative is to activate a “no-fill” mode where the memory accesses are serviced from the cache when they hit it, but accesses that miss the cache are serviced directly from the memory:

• 1.   Preload the AES tables into the cache

• 2.   Activate the “no-fill” mode

• 3.   Perform encryption

• 4.   Deactivating “no-fill” mode

The section spanning (1) and (2) is critical, and attacking process must not be allowed to run during this time [16]. However, the major drawback of this approach is that during the encryption process the overall system will be slowed down by a factor since cache access is limited during the encryption process. However, using RAT, the “no-fill” mode is not required. All the other processes can be allowed to access the cache even during the encryption proceeds.

Dynamic Table Storage. The cache-based attacks observe memory access patterns to learn about the table lookups. Instead of eliminating these, we may try to de-correlate them. For example, one can use many copies of each table, placed at various offsets in memory, and have each table lookup use a pseudo randomly chosen table. By utilizing more compactly, one can use a single table, but pseudo randomly move it around memory several times during each encryption [16]. But the major drawback of this approach is that it will incur cache misses more than ever.

This implies that the encryption process will be slowed down by a factor. More importantly, the performance and security of this approach are largely architecture dependent. Using RAT helps us alleviate this situation by obviating the need of moving around the Lookup table in the memory.

• A. Other Major Advantages

Some important benefits of using the RAT are as follows:

• VI. Future Works

The findings we have presented in this paper have thrown up few new questions that need further investigation. In the remainder of this section, we discuss future work to extend the scope and applicability of this work.

• •    There are some limitations in the process of constructing the RAT table. One major limitation is that swapping is not allowed more than once for an entry. Thus, there can be a maximum of 128

swaps for a single Lookup table. To allow more number of swaps per entry, more sophisticated data structure is required.

• •    The big picture that summarizes the performance difference with the straightforward Table lookup approach is given below. As we can see, we need 2 times more table lookups than the ordinary approach. The area of future development is to reduce this particular factor.

• •    Another big concern is that RAT tables add a fair amount of memory overhead to the encrypting process. Whereas the Lookup tables altogether require 4KB of space, RAT tables requires 1KB of space. Although this is not a big amount, space overhead can be reduced with the assistance of some more tables of smaller sizes.

• VII. Conclusions

It is apparent that Side channel attacks do not divulge everything at once; instead they ease the calculations and assumptions that helps rest  of the operations accomplished in a bounded time. Although the existing AES encryption model has sufficient complexity to blow away any straightforward attempt to break the security, side-channels still poses a real threat and a bad implementation of the cipher might lead to dire consequences. The most challenging part of security is now making the implementation of the existing ciphers resistant to side-channel attacks. Preventing leakage of information through side-channel is not a trivial task at all. The empirical observation presented in this paper has shown that even the straightforward Table lookup approach can be made secure without the assistance of any piece of special software or hardware, which is widely acknowledged requirement in the real settings.