An Efficient (n, n) Visual Secret Image Sharing using Random Grids with XOR Recovery

Published Online November 2019 in MECS

Visual Cryptography Scheme (VCS) is a method of Visual Secret Sharing (VSS) suggested by Naor and Shamir that suggest the retrieval of image by stacking the share of the image without any cryptographic computational efforts [1]. In VCS, an original image is encrypted into different images called shares.VSS schemes require k-out-of-n shares to get the original image. Each share (Random binary pattern) has been distributed among ‘n’ participants. Single share cannot retrieve complete information about original image, at least k-out-of-n (k is subset of n) shares are needed. Using human visual system (HVS), we can easily retrieve the original image with the stacking of these shares together, without any computation and cryptographic knowledge. This process is called VCS with OR stacking. In this type of method, we can retrieve not more than 50 % visual quality. To measure the visual quality of the retrieve image, we calculate the contrast of the image. We discussed the contrast calculation in section IV. We can also retrieve the secret image with XOR stacking. In this approach, we use XOR operator for stacking to produce retrieve the original image with high visual quality. Traditional VCS reports the pixel expansions i.e. shares generated are more in size than the actual image. VCS produces both meaningful and random (non-meaningful) shares.

G. Ateniese et al. developed a threshold k-out-of-n VCS method [2]. The technique proposed by G. Ateniese et al. [2] reports better results than the scheme suggested by Naor and Shamir [1] with less pixel expansion. Ito’s et al. [3] removes the problem of pixel expansion in their research i.e. retrieve image after stacking and original image both are equal in size.

VSS by random grids (RG) removes the pixel expansion problem and there is no requirement of codebook design. Kafri and Keren [4] proposed the overview of RG. It is 2D array consists of pixels. With the use of coin flip method, we got every pixel, either fully transparent or opaque in a random manner. The transparent pixel (white) passes the light and opaque pixels (black) stop the light. The numbers of transparent pixels and opaque pixels are same in random grid [5] probabilistically. Table 1. presents the results after superimposing of the two random pixels k 1 & k 2 . According to their scheme the secret image is encrypted into two meaningless RG.

Table 1. Results after superimposing of two random pixels

k 1	k 2	k 1 ⊗ k 2
0	0	0
0	1	1
1	0	1
1	1	1

This paper is arranged as follows: Sections II discusses the literature review and concept of Visual Secret Sharing (VSS) using random grids. Section III defines the proposed method. Section IV defines the performance analysis. The different experimental results are discussed in section V. In the end, Section VI concludes the proposed technique.

Table 2. Notations used in this paper

SNo	Notations	Descriptions
1	1(resp. 0)	A Black( resp. White) pixel
2	I 1 ,I 2 ………I n	Shares generated
3	⊗	OR operation for stacking
4	⊕	XOR operation for stacking
5	I	Original Secret Image
6	I S	Secret Image after stacking

Table 3. Abbreviations used in this paper

SNo	Abbreviations	Descriptions
1	VCS	Visual Cryptography Scheme
2	VSS	Visual secret image sharing
3	HVS	Human Visual System
4	RG	Random Grid
5	PVCS	Progressive VCS

• II.    Literature Review

Encryption of secret image (binary) based on RG was first proposed by Kafri and Karen [4]. They proposed three algorithms for encrypting the image into RGs. The principle of one of the algorithm is described in Fig.1. A secret pixel is taken from the secret binary image and is encrypted into the subpixels in each of the two RGs. The subpixels are selected randomly form the two columns under the certain secret pixel. There is the random selection so that each column is selected with 50% probabilities. In that fashion the first sub pixel is assigned to RG1 and the followed up pixel is assigned to RG2 this process follows up till the last pixel of the secret image. So it confirmed that individual share cannot give any clue about the secret image. When we stack these shares the black pixels will cover the white pixels, and the white pixel will decode into the black or white pixel with 50% probabilities. This scheme is known as RG-based (2, 2) VC. The size of the shares is same as that of the secret image. There is some loss of contrast in the revealed image but we can clearly identify the image.

• S.    J. Shyu [6] further extend their work proposed in [5] for encrypting the image with multiple RG. This is a method of image encryption using the visual cryptograms

of n ≥ 2 . Chen and Tsao [8] developed a User-friendly VSS based on RG. In this method, they produce meaningful shares using cover image without the pixel expansion. They analyze their method with the method developed in [7] in terms of share type, contrast, pixel expansion and image format etc.

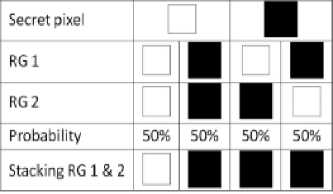
Fig.1. RG based 2 out of 2 Visual Cryptography Scheme

In (k, n) threshold VSS, we require only k shares to retrieve the secret image. T. H. Chen and K. H. Tsao [9] proposed a new threshold (k, n) VSS using RG for color and binary images. The developed method gives good visual quality and security. We cannot reveal image with less than k shares.

Y. C. Hou et al. [13] developed a method based on RG in which they produce random and meaningful shares using different cover images. This method gives good result as compared to the method proposed by Chen and Tsao [8]. Yang, C. N. et al [14] investigates the relation between OR based VCS and XOR based VCS. Y. C. Hou et al. [15] developed a novel scheme that allows different privileges to different participants.

There are two methods for stacking the shares to retrieve the original image. One is OR based and other XOR based stacking. Using XOR we get better visual quality. Duanhao Ou et al. [16] developed a XOR based (n, n) VCS and produce meaningful shares.

Xuehu Yan et al. [17] proposed threshold (k, n) VCS with multiple decryption method such as OR and XOR based stacking. We can also apply this method for color images or grayscale images. Yan, X. et al [18] developed a RG based VSS and use OR and XOR decryption method.

Xuehu Yan et al. [19] proposed a novel threshold VSS based on RG which progressively increased the visual quality. With increasing the stacked shares, the visual quality of retrieve image is also increased. This method is known as Progressive VCS (PVCS).Pei-Ling Chiu et al. [20] developed a user friendly PVCS using XOR and produce meaningful shares.

Her-Chang Chao et al. [21] also proposed a RG based PVCS with XOR ability. Yan, X. et al [22] analyze the visual quality and difference between related methods and proposed new threshold VSS scheme using RG.

VSS can be applied in many areas of research, authentication, and security of information. In this paper, we developed (n, n) VSS based on RG using XOR to retrieve 100% visual quality of original image.

Table 4. gives the performance measures of different

VSS discussed in [23]. This table gives the comparative study of different VSS based on different parameter such as pixel expansion, decryption method and type of VSS. This study helps to choose secure and suitable method for particular problem base on different parameters.

Table 4. Performance measures of various VSS

SNo.	Schemes	Pixel Expansion	Meaningful Shares	Decryption Method	Type of VSS
1	Ours	No	No	XOR	n out of n (n>=3)
2	[1]	Yes	No	OR	k out of n
3	[2]	Yes	No	OR	n out of n k out of n
4	[4]	No	No	OR	2 out of 2
5	[5]	No	No	OR	2 out of 2
6	[6]	No	No	OR	n out of n
7	[7]	No	Yes	OR	2 out of 2
8	[8]	No	Yes	OR	2 out of 2
9	[9]	No	No	OR	k out of n
10	[12]	Yes	No	XOR	n out of n
11	[13]	No	Yes	OR	2 out of 2
12	[14]	No	No	OR	k out of n
13	[16]	No	Yes	XOR	n out of n
14	[17]	No	No	OR, XOR	k out of n
15	[19]	No	No	OR	k out of n
16	[20]	No	Yes	XOR	2 out of n
17	[21]	No	No	XOR	2 out of n

• III.    Proposed Method

In the proposed method, input is image (Binary). The size of image is A × B. First we generate n-1 shares using random grid, then generate share n by the proposed algorithm 1. For decryption, use algorithm 2. Diagram for share generation is shown in Fig.2.

There are eight steps to generate n shares for n out of n secret image sharing in proposed method. We take a secret image (I) of size A ×B and create n-1 shares in random way i.e. put random pixels in I1, I2, I3………………… In-1 using step 1 and 2. For nth share, we use step 4 to 8 of algorithm 1. We generate a matrix X of size A ×B using step 4then we calculate the pixel (i, j) of nth share using X and the original secret image I using step 5 to 8. In this way we create all n shares. Using algorithm 2, we simply reconstruct the secret image IS completely without loss of information.

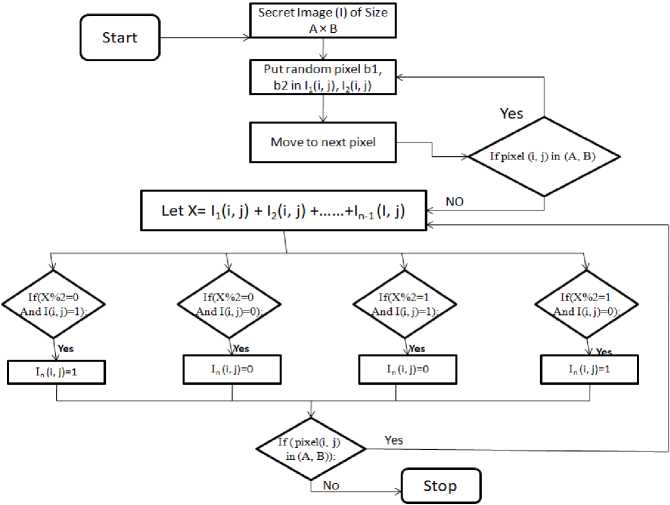
Fig.2. Share generation procedure of XOR based (n, n) VSS using random grid

Algorithm 1: For Encryption

Input: A ×B binary image (Secret image) I

• 1:     For every position (i,j) ∈ {(i,j) 1 ≤ i ≤ A ;1 ≤ j ≤ B }

repeat step 2

• 2:    Put random pixel    b 1 , b 2 , b 3.................. b n - 1 in

• 3:    For every position (i,j) ∈ {(i,j) 1 ≤ i ≤ A ;1 ≤ j ≤ B } rep eat step 4-8

• 4:    Let X = I 1 ( i , j ), I 2 ( i , j ).................. I n - 1 ( i , j )

• 5:    if X%2=0 and I(i,j)=1 then In(i,j)=1

• 6:    if X%2=0 and I(i,j)=0 then In(i,j)=0

• 7:    if X%2=1 and I(i,j)=1 then In(i,j)=0

• 8:    if X%2=1 and I(i,j)=0 then In(i,j)=1

Algorithm 2: For Decryption

Output: A × B binary secret image I

• 1:     For every position (i,j) ∈ {(i,j) 1 ≤ i ≤ A ;1 ≤ j ≤ B }

repeat step 2

• 2:    I s = I 1 ( i , j ) ⊕ I 2 ( i , j ) ⊕ I 3 ( i , j )................. ⊕ I n ( i , j )

• 3:    S ecret image I

• IV.    Performance Analysis

Definition 1 (Contrast): An important measure of VCS is contrast of the reconstructed image i.e. visibility of the secret image. We can calculate the Contrast (α) of the retrieve image using

α = ( Α 0 -Α 1 ) / (1 + Α 1 )             (1)

the original secret image A1= Probability of wrongly decrypted the One’s of original secret image

Definition 2 (Security): Security condition means that we can retrieve original image with insufficient shares.

Proof:  According to step 2, the shared pixel is independent of the secret pixel; no matter the secret image is 0 or 1. Only nth share is dependent on secret image in step 4 to 8 but it is insufficient to retrieve image with only nth share. So, each share has no clue about secret image.

Definition 3 (Visually recognizable): The retrieve image I s is recognizable as original image by α >0. If α =1, then the image is fully retrieved.

• V.    Results

The proposed method results show the 100% recovery of the image after stacking the shares. Fig.3. shows the experimental result of (3, 3) threshold VSS on binary image Baboon: 512* 512 pixels using proposed method. The contrast of Fig.3 (e) is 1. Fig.4. shows the experimental result of (4, 4) threshold VSS on binary image Baboon: 512* 512 pixels using proposed method. The contrast of Fig.4 (f) is 1. Fig.5. shows the experimental result of (5, 5) threshold VSS on binary image Baboon: 512* 512 pixels using proposed method. The contrast of Fig.5 (g) is 1. Fig.6. shows the experimental result of (3, 3) threshold VSS on binary image Lena: 512* 512 pixels using proposed method. The contrast of Fig.6 (e) is 1. Fig.7. shows the experimental result of (4, 4) threshold VSS on binary image Lena: 512* 512 pixels using proposed method. The contrast of Fig.7 (f) is 1. Fig.8. shows the experimental result of (5, 5) threshold VSS on binary image Lena: 512* 512 pixels using proposed method. The contrast of Fig.8 (g) is 1.

Where A 0 = Probability of correctly decrypted Zero’s of

Fig.3. The experimental result of (3, 3) threshold VSS. 3(a): baboon image, 3(b)-(d): Shares 1-3, 3(e): Image after stacking using XOR.

Fig.4. The experimental result of (4, 4) threshold VSS on binary image Baboon: 512* 512 pixels using proposed method. 4(a): Baboon image, 4(b)-(e): Shares 1-4, 4(f): Image after stacking using XOR

Fig.5. The experimental result of (5, 5) threshold VSS on binary image Baboon: 512* 512 pixels using proposed method. 5(a): Baboon image, 5(b)-(f): Shares 1-5, 5(g): Image after stacking using XOR.

Fig.6. The experimental result of (3, 3) threshold VSS on binary image Lena: 512* 512 pixels using proposed method. 6(a): Lena image, 6(b)-(d): Shares 1-3, 6(e): Image after stacking using XOR.

Fig.7. The experimental result of (4, 4) threshold VSS on binary image Lena: 512* 512 pixels using proposed method. 7(a): Lena image, 7(b)-(e): Shares 1-4, 7(f): Image after stacking using XOR.

Fig.8. The experimental result of (5, 5) threshold VSS on binary image Lena: 512* 512 pixels using proposed method. 8(a): Lena image, 8 (b)-(f):Shares1-5, 8(g): Image after stacking using XOR.

• VI.    Conclusion

For data (Image) transmission over the internet, we have to be considering the security and simplicity aspect. One method is data encryption. Another way is visual secret sharing schemes, these are easy in implementing and at the receiver end, and we have no need of computation for decryption process. This paper gives a new approach of (n, n) visual secret image sharing method using random grid based on XOR recovery. Table 4. gives the comparative study of different VSS with our method to show the performance measure. Section 5 describes the contrast, security, visual recognizable definition and proof to show this method is easy to implement, secure and good visual quality without pixel expansion. Experimental results are shown that this method is easy to implement and we retrieve the secret image completely without loss of information. To improve the visual quality of retrieve image in case of meaningful shares will be the future work.