An Efficient Technique for Optimality Measurement of Approximation Algorithms

The minimum vertex cover is a very popular NP-complete problem like other famous NP-hard problems including maximum independent set (MIS) and maximum clique (MC), and so forth. The maximum independent set (MIS) contains those vertices in G = ( V , E ) that are not in MVC, such as

MIS = G ( V , E ) - MVC ( G = ₍ V , E ) ) and vice versa. Similarly, the maximum clique contains those vertices in G = ( V , E ) that are in MVC of complement graph such as MC = G = ( V , E ) - MVC (), where a complement graph is an undirected graph E = { ( vi , vj ) | vi , vj e V , i ^ j , ( vi , vj ) ^ E } , hence solving the MVC will definitely solve all NP-complete problems [1].

A polynomial-time algorithm that has the capability to solve the MVC problem has not been devolved to date. It is also not possible for an algorithm to prove a super polynomial-time bound for MVC. We can solve the MVC problem in two ways, either by using the approximation algorithms or exact algorithms. The approximation algorithm can solve the MVC problem in polynomial time but no guarantee of optimality. The exact algorithms provide the exact solution of the problem, but as time goes on they require increases exponentially with the size of the problem. Hence, the approximation algorithms are the better choice where the size of the problem is large, and the solution requires does not to be optimal. The exact algorithm is the best choice where the size of the problem is small with no time constraint. However, the issue arises where the size of the problem is large, and the optimal solution is required in a short time. Hence, we need a technique to measure the optimality of approximation algorithms [2].

The minimum vertex cover (MVC) is normally used in different real-world applications. The approximation algorithms have been successfully used for the solution of the MVC problem. The approximation algorithms provide a near-optimal solution within a reasonable time [3]. The placement of guards in museums is the real-time application of the MVC. Furthermore, the MVC problem can also be used for the construction of hospitals, schools and so forth so that they can cover the maximum area and the maximum number of people can easily approach the hospitals and schools [2]. Due to these applications, the MVC problem has grasped the attention of many researchers in the last decades, and a lot of methods have been proposed to solve this problem.

Cook in 1971 has divided all problems into classes named polynomial-time problems (P-Problems), non-deterministic polynomial-time problems (NP-Problems), NP-hard problems and NP-complete problems [1]. A problem that can be sorted out in a specific time is called polynomial-time problems or P-Problems. Examples of p-problems are the complement of a graph, subtraction of a set of vertices from a graph. As opposed to polynomial time, the NP problem cannot be solved in a specific but rather require exponential time to be solved. By using the current computation resources, it is impossible to solve a large NP problem at a specific time. There are a lot of NP-problems, such as traveling salesman problem, graph coloring problem, and MVC problem, and so forth. According to Cook, the NP-complete problem retains two properties which are; the problem should be NP and reducible in polynomial time to the NP-complete problem [1]. The fundamental problem of the NP-complete set is Boolean satisfactory (SAT). The other problems that can be converted in SAT Problem in polynomial time are clique problem, MIS, and so forth. MVC can also be converted to MIS in polynomial time hence included in NP-complete problem set [13].

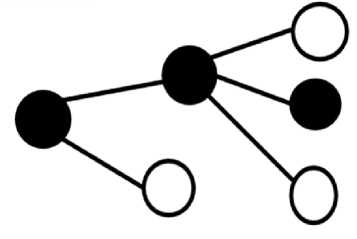
A vertex cover ( V , C ) in an undirected graph G = ( V , E ) is a subset of vertices which covers all the edges in a graph, but as in MVC that VC should be minimum [2]. In Figure 1 the filled vertices represent the vertices in vertex cover, and the empty vertices represent that the vertices do not belong to vertex cover in a graph.

(a)

(b)

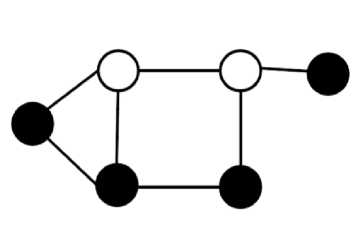
Fig. 1. (a) Graph with three vertices in vertex cover and (b) Graph with four vertex cover.

The least vertex cover in a graph is recognized as the MVC. The vertex cover will be represented by X , that denotes MVC size, i.e. X = | C | [3].

The MVC solutions have two main categories, namely approximation algorithms and exact algorithms. Approximate algorithms solve the problem in a reasonable time with guaranteed optimality. Approximation algorithms provide a near-optimal solution in a reasonable time. Approximation algorithms are useful when the size of the problem is large, and the solution is required at a reasonable time. The exact algorithms provide a guaranteed optimal solution, but time-explosion occurs as the dimension of the problem grows. For solving a moderate size problem, it can take billion or trillion years with currently available computation power [4,5]. The MVC problem can be efficiently tackled by using approximation algorithms while for the clique problem; complete algorithms are the best choice. The approximation algorithms can be used to solve a problem where the near-optimal solution is required within no time. The problems in which optimality has a critical concern and cannot be compromised even in a long time, to solve these problems complete algorithms are the best choice.

It is difficult to design a better complete algorithm for the MVC problem due to its complex nature. Most of the developed algorithms for the MVC problem are approximation algorithms. In applications where optimality is required within no time we cannot apply approximation algorithms because of optimality constraint, and also the exact algorithm cannot be deployed due to its low computational complexity.

The problem of MVC is an earlier NP problem which was proven NP-complete [6]. The algorithms have limitations so the NP-complete problems cannot be solved with polynomial-time algorithms. Also, the algorithms do not have the capability to prove a super polynomial-time bound for any of these problems.

The MVC problem can be divided into weighted and un-weighted [7]. In addition, the MVC problem can be divided into two versions, i.e. optimization and decision. In the optimization version, the algorithm has to find the best solution from the available feasible solutions. In the decision version, the algorithm has to find the existence of the desired size of ' k ' , where k is the mvc [8]. t his paper deals with the un-weighted MVC problem. The important preliminaries are presented in the subsequent section for a better understanding of the algorithms.

• 1.1.    Preliminaries

  • 1.1.1.    We are concerned with an undirected graph G = ( V , E ) throughout this paper, where V represents the number of vertices and E indicates the number of edges.

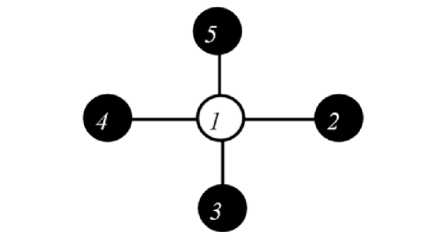
  • 1.1.2.    For a vertex v e V , let deg ( v ) is the set of edge occurrence to it, the minimum degree is represented by 5 in G = ( V , E ) .

    1.1.3.

    that

    
    

    A graph is indicate complemented graphs such

    
    

    g = ( v , e )

    
    

    ^,

    
    

    where

    
    

    E = { ( vi, vj ) I vi, vj e V , i * j, ( vi , vj ) ^ E } .

    
    

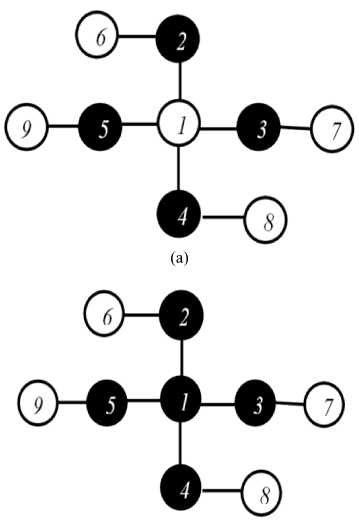
    The maximum degree greedy (MDG) algorithm fails to provide the optimal result on some benchmark graphs as shown in Figure 2. The shape • represents a vertex in vertex cover and vertex not in the vertex cover is represented by the shape .

    
    

Where Ap is an approximate algorithm for the MVC, symbols ←, ∆ and δ are used for assignment, maximum degree, and the minimum degree respectively.

In this paper, we have proposed a method named as optimality measurement of approximation algorithms (OMAA). The purpose of the problem algorithm is to measure the optimality of approximation algorithms for the minimum vertex cover problem. The time requires to solve a problem by using the complete algorithm increase exponentially as the size of the problem increase. Hence, we need a solution to find the optimal solution in a reasonable time. Hence, in the proposed approach we have proposed a technique to check the optimality of an approximation algorithm. Hence, the proposed approach is a better choice in a situation where optimal results are required for large graph instances in a reasonable time. This method provides the opportunity to check whether the result returns by an approximation algorithm for the minimum vertex cover problem is optimal or not.

The paper structure organization is carried out as: the literature review has been carried out in section 2, the suggested scheme has been explained in sections 3, section 4 contains evaluation and results, section 5 contains discussion, and finally, the paper is concluded in section 6.

(b)

Fig. 2. (a) Optimal Vertex Cover. (b) Vertex Cover Returned by MDG.

• II.    Related Work

In this section, the literature review of some well-known state of the art algorithm has been carried out for the MVC problem; all the selected algorithms are approximate algorithms.

The simplest algorithm that was initially developed for MVC is MDG [9]. The MDG is the alternative form of set cover algorithm suggested by Chavatal et al. in [10]. In this approach, initially, each node degree is calculated in the graph, and that node is selected as the MVC node having the highest degree.

The maximum degree greedy (MDG) approach calculates the degree continuously until a maximum degree node has been found out. The network bench model is used for the calculation of the degree in MDG, which takes O (E) steps. The technique is so simple and works on the simple steps, but the best solution is not guaranteed in greedy approaches, the same is the issue with MDG. When MDG selects a node for the calculation of maximum degree for vertex cover, there is no surety that the selected vertex is part of maximum vertex cover or not. There is a possibility of selection of extra vertexes that can cause poor results. The computation complexity is reasonable, therefore preferred over other approximation algorithms.

The worst runtime complexity of the maximum degree greedy (MDG) is O (E2), which indicates the computation efficiency of the MDG algorithm.

Another simple heuristic algorithm is the modified vertex support algorithm (MVSA) [11] which is achieved by modifying the vertex support algorithm [12]. The same data structure has been introduced in MVSA as in VSA. First, the calculation of each node degree is carried out then the least degree node is chosen and the resultant node is considered as MVC node having minimum support values in the neighbor is selected as MVC node.

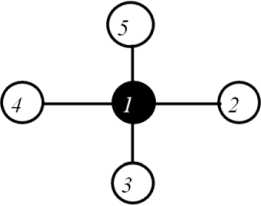
The MVSA is computationally efficient; the decisions are made straightforward. The runtime complexity of the modified vertex support algorithm (MVSA) is O (EV2log v). The MVSA also fails to deal with small instances as in Figure 3.

(a)

(b)

Fig. 3. (a) Optimal Vertex Cover. (b) Vertex Cover Returned by MVSA

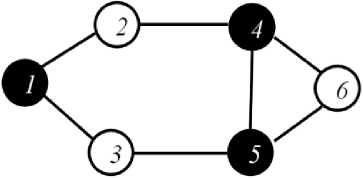
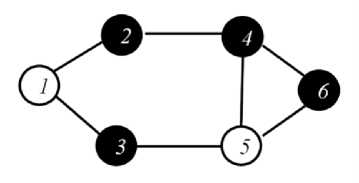
The clever steady strategy algorithm (CSSA) is a simple approximate algorithm for solving the MVC problem [13]. The algorithm first locates the minimum degree vertex and then its entire neighbor vertices are searched out, the minimum degree vertex in all neighbors of the vertex having the least degree will be selected for adding to the vertex cover.

The clever steady strategy algorithm (CSSA) does not provide an optimal solution on some benchmark instances as shown in Figure 4.

(a)

(b)

Fig. 4. (a) Optimal Vertex Cover. (b) Vertex Cover Returned by CSSA.

The other most prominent near-optimal algorithms proposed for the MVC problem, are; vertex support algorithm (VSA) [12], advanced vertex support algorithm (AVSA) [14], degree contribution algorithm (DCA)[15], max degree around (MDA) algorithm [2], mean of neighbors of minimum degree algorithm (MNMA) [16], and the maximum adjacent minimum degree algorithm (MAMA) [17].

• III.    Proposed Method

An algorithm time that has the potential to provide the optimal solution of the MVC problem has not been devolved to date. It is also not possible for an algorithm to prove a super polynomial-time bound for MVC. We can solve the MVC problem in two ways, either by using the approximation algorithms or exact algorithms. The approximation algorithm can solve the MVC problem in polynomial time but there is no guarantee of optimality. The exact algorithms provide the exact solution of the problem, but with time, they increases exponentially with the size of the problem. Hence, the approximation algorithms are the better choice where the size of the problem is large, and the solution requires does not to be optimal. The exact algorithm is the best choice where the size of the problem is small with no time constraint. However, the issue arises where the size of the problem is large, and the optimal solution is required in a short time. Hence, we need a technique to measure the optimality of approximation algorithms in this section, a novel technique has been suggested for optimality of an approximation algorithm, and if the approximation for a certain application is optimal when there is no need to deploy multiple approximate algorithms for it.

The proposed approach will also evaluate the optimality of approximate algorithms for the MVC problem. In the proposed approach, first the complement of the graph will be carried out then approximate algorithm for MVC will be deployed on it and the output result will be saved in C. Afterward the nodes in the VC will be subtracted from the vertices in G= (V, E) and the result will be saved in P.

Furthermore, the minimum degree vertex in G = (V, E) will be calculated, if the degree of minimum degree vertex becomes less than P, then it will be removed from G = (V, E) and the graph will be updated. The process continues until the graph becomes empty or the degree of minimum degree vertex becomes equal or greater than P. If the graph becomes empty, it means that the solution of the deployed approximation algorithm is optimal. In the second case if after deleting the vertex when a situation arises where the degree of a minimum degree vertex becomes greater or equal to P, then it means that the solution provided by the approximation is not optimal.

The detailed flow diagram of the suggested technique is provided in the following Figure 5.

START

Input G=(V,E)

Complement the graph as G’=|

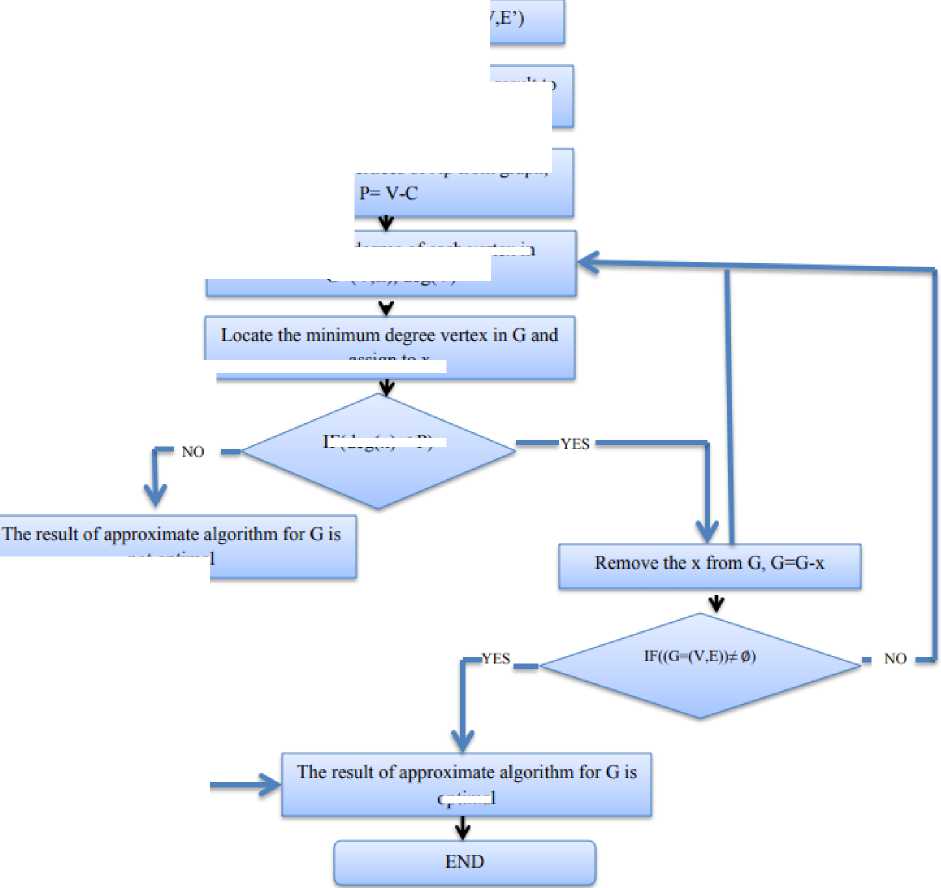
optimal not optimal

Fig. 5. Flow diagram of the proposed algorithm

Apply Ap on G’=(V,E') and assign result to C

Subtract MVC vertices of Ap from graph,

Calculate the degree of each vertex in G-(V,E), deg(V)

assign to x

lF(deg(x) < P)

• IV.    Evaluation And Results

In this section, we have applied some well-known approximation algorithms on the small benchmark graphs to elaborate on the working mechanism of the proposed approach better. There are numerous approximation algorithms for solving the MVC problem. We have selected the maximum degree greedy (MDG) algorithm, modified vertex cover algorithm (MVSA), and clever steady strategy algorithm (CSSA), the detailed description of these methods is provided in the literature review section. The selected methods are approximate having different working mechanisms.

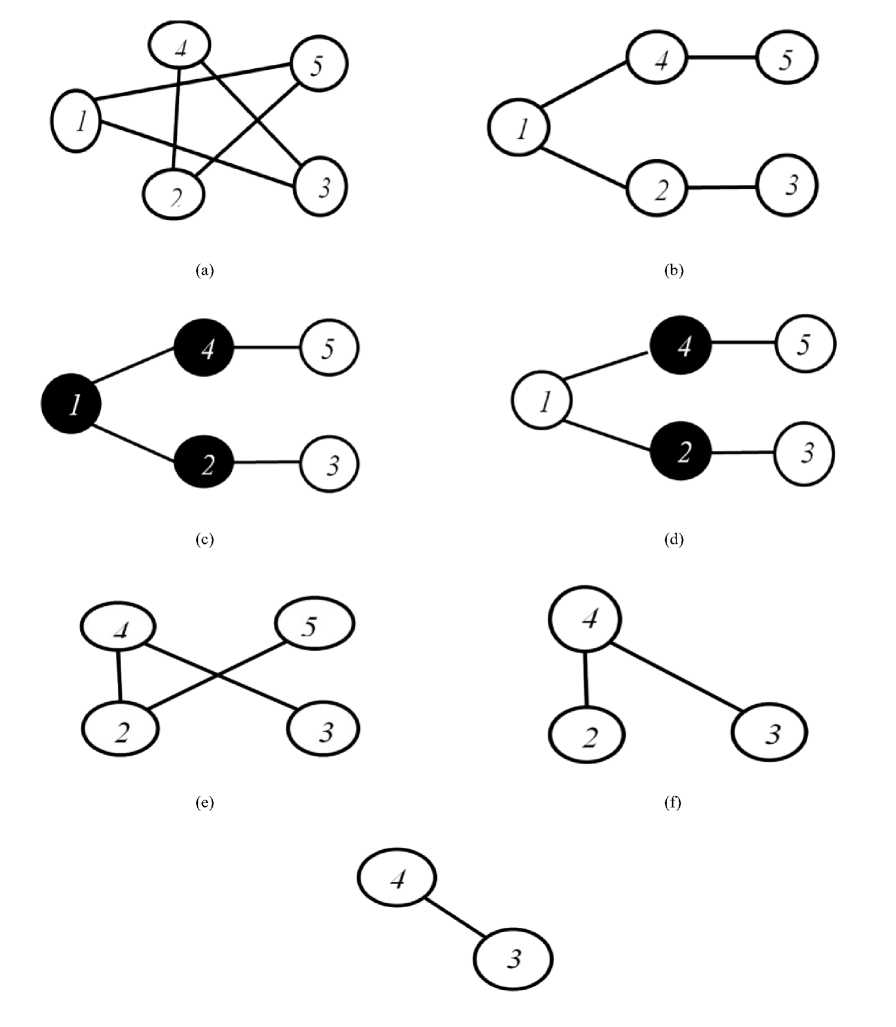
(g)

Fig. 6. (a) Given Graph G= (V, E). (b) Complemented Graph G= (V, E’). (c) Vertex Cover returned by MDG. (d) Vertex Cover returned by MVSA and CSSA. (e) Updated Graph Given by MVSA and CSSA. (f) Reduced Graph Given by MVSA and CSSA. (g) Final Graph Given by MVSA and CSSA.

The proposed method starts with complementing the graph given in Fig. 6(a)., The graph complementation is the essential step of the proposed method before applying any processing. After the graph complementation, we applied the Maximum Degree Greedy (MDG) approximation algorithm given in Figure 6(b). The vertex cover by any algorithm depends upon the strategy of the selection of the first vertex of the graph. The maximum degree greedy (MDG) algorithm covers the complemented graph in 3 vertices (if the vertex 1 is selected first) as shown in Figure 6(c), hence according to the proposed approach it will be saved in C (C ←3), then P will be calculated, i.e. P←5-3=2. In step 3, each node degree of the graph in Figure 6(a) will be calculated, such as 1(2), 2(2), 3(3), 4(2), and 5(3). Afterward, the minimum degree vertex will be located, in the given graph. In case of the vertices 1, 2 and 4 having the same minimum degree, one of them will be selected, (we selected the vertex 1) and the degree of the same will be compared to P. The P-value is equal to the minimum degree that proves the solution provided by Maximum Degree Greedy (MDG) algorithm is not optimal.

Table 1. Pseudocode for Optimality Measurement of Approximation (OMA) Method

Input: G= (V, E)

Output: Optimality

Begin:

• 1.    C← Ap (G’= (V, E’))

  // apply approximate algorithm on the completed graph.

• 2.    P ← V- C

  // subtract the minimum vertex cover from G.

• 3.    FOR i←1 to V { i. deg(vi) }

  // compute each node degree.

• 4.    x← δ (G=(V,E))

  // compute the minimum degree node in G= (V, E).

• 5.    IF (deg(x) < P) {i. G= (V, E) ←G= (V, E)-x} //Remove the least degree vertex from G= (V, E), G=G-x.

• 6.  IF((G=(V,E))=∅) {result of Ap is optimal go to End }

  // If the graph become empty.

• 7.    IF (deg(x)=>P) { result of AP is not optimal go to End}

  // If the degree of the minimum degree vertex becomes greater or equal to P.

• 8.    Else Go to step 3.

End

Similarly, the proposed technique was applied to the MVSA on the complemented graph Figure 6(b). The MVSA covers the graph in 2 vertices as shown in Figure 6(d), hence C←3. The vertices 1, 2 and 4 have the same minimum degree vertices (the degree is 2), so we have selected vertex 1 randomly. Whereas, the comparison of P-value and the minimum degree value take place where P-value is greater than the minimum degree value. Hence the vertex 1 will be removed from the graph, and the graph will be updated as shown in Figure 6(e). Again the minimum degree vertex degree will be equal to 2 which is less than P-value, (all have the same degree, we selected vertex 2 randomly), hence it will be removed from graph 6(e) and again the graph will be updated as shown in Figure 6(f). Now the minimum degree vertices were 2 and 3 having the degree 1, we selected 1, compared with P-value and removed from graph Figure 6(f) and the graph will be updated as shown in Figure 6(g). Next the minimum degree was equal to 1 of both remaining vertices (4 and 3) of graph Figure 6(g), we selected vertex 4, its degree was less than P, so removed from graph Figure 6(g), after this vertex deletion the graph became empty which indicates that the solution returned by Modified Vertex Support Algorithm (MVSA) was optimal. Hence no need to apply any further approximation algorithm.

If we apply the CSSA algorithm on the graph given in Figure 6(a), it will return the same result as provided by MVSA. The MVSA and clever steady strategy algorithm (CSSA) both are optimal on the graph Figure 6(a). Eventually, the CSSA and MVSA algorithms are the best choices for the stated graph Figure 6(a).

We have also applied the CSSA, MVSA, and MDG algorithms on large graph instances for proper evaluation of the proposed method. The benchmark instances are taken from two public libraries namely DIMACS [18]

and BHOSLIB [19]. Approximation ration formula is given in Equation 1 in order to check the performance of approximation algorithms, pi = Ip- > 1              (1)

Ik

Here pi represents the approximation ratio, Ai represents the approximate solution and OPTi represent the optimal solution of a problem. After putting values in I k and I *_k in equation 1, if pi = 1 it indicates that the solution is optimal. More deviation from 1 specify that the solution is poor [13].

• V.    Discussion

We have applied the algorithms on graphs 2, 3, and 4. The Maximum Degree Greedy (MDG) fails to provide an optimal solution on the graph given in figure 2. The MVSA fails to provide the best solution on the graph given in figure 3 and Clever Steady Strategy Algorithm (CSSA) fails to provide an optimal solution on the graphs given in figure 4. On the graph given in figure 2 the Maximum Degree Greedy (MDG) fails to provide an optimal result, but on the same graph, Modified Vertex Support Algorithm (MVSA) and Clever Steady Strategy Algorithm (CSSA) return optimal solution. On the graph given in figure 3, Modified Vertex Support Algorithm (MVSA) fails, but Clever Steady Strategy Algorithm (CSSA) and Maximum Degree Greedy (MDG) provide optimal solutions. Similarly, on the graph in figure 4 the Clever Steady Strategy Algorithm (CSSA) and Modified Vertex Support Algorithm (MVSA) both fail, but Maximum Degree Greedy (MDG) returns optimal solution.

This strategy was needed to test that either the given approximation algorithm provides an optimal solution for a graph or not. These results reveal the importance of the suggested evaluation method of the approximate algorithms for the MVC problem.

• VI.    Conclusion

The proposed method evaluates the optimality of approximation algorithms for the MVC problem. The basic determination of developing this technique was to save time and test the application compatibility of an approximation algorithm of MVC for a particular problem. The proposed methods have been evaluated on small benchmark instances for better understanding. The proposed method is good in such a condition where we have a lot of approximations algorithms and we need a better choice for a benchmark instance(s).

In the future we would like to test the proposed method on large graph instances as well by using some standard libraries. We will also use the same idea for other NP- complete, such as maximum independent set and clique etc.