An Encryption Technique based upon Encoded Multiplier with Controlled Generation of Random Numbers

Published Online September 2015 in MECS DOI: 10.5815/ijcnis.2015.10.06

Cryptography has remained important over the centuries, used mainly for military and diplomatic communications. With the advent of the internet and electronic commerce, cryptography has become vital for the functioning of the global economy, and is something that is used by millions of people on a daily basis.14 Secure transmission of data between one person to another has built up some challenges as intruders have found explicit interest in interfering in personal as well as confidential communication between two parties. Cryptography is a technique of securing contents of a message by using various algorithms. The concept of cryptography boomed with the huge incoming reports of safety breaches where confidential messages became vulnerable to attacks. Data secrecy is mainly dependent on the strength of key size in the encryption algorithm. Various encryption algorithms ranging from some below mentioned algorithms to DNA cryptography to variations in RSA algorithms have cropped up so that sensitive and confidential information can be stored and transmitted across insecure networks so that unauthorized persons cannot retrieve the exact message.

A number of network security algorithms based on cryptography make use of random numbers. Some of those examples are mentioned below:

• •    Key distribution and reciprocal authentication schemes: In such schemes, two communicating parties cooperate by exchanging messages to distribute keys and/or authenticate each other. In many cases, nonces are used for handshaking to prevent replay attacks. The use of random numbers for the nonces frustrates an opponent’s efforts to determine or guess the nonce.

• •    Session key generation: A secret key for symmetric encryption is generated for use for a short period of time. This key is generally called a session key.

• •    Generation of keys for the RSA public-key encryption algorithm. A significant improvement over the original algorithm.

• •    Generation of a bit stream for symmetric stream encryption.

These applications give rise to two distinct and not necessarily compatible requirements for a sequence of random numbers: randomness and unpredictability.11

This paper proposes such an encryption technique which can keep intruders away from knowing the actual contents of the message. Creating a chaos among a certain level of order without the conscience of even the sender but in a controlled manner certainly ensures a different view of randomness through this paper. The involvement of an already experimented technique of encoded multiplier adds upon another level of security alongside the random number concept. Random numbers are those numbers that occur in a sequence such that the future value of the sequence cannot be predicted based on present or past values. Random numbers find application in statistical analysis and probability theory. The many applications of randomness have led to the development of random number generating algorithms. These algorithms generate a sequence of random numbers either computationally or physically.11 Hash keys are like records which are meant to be broken but the concept of random number generation based upon a secure line conversation for each message makes things worse for the intruder to break the text as each message has an individual character equivalence array for all the possible printable characters.

• II.    Terminology

• A.    Cryptography

The art and science of keeping messages secure based upon some algorithm in context of encrypting as well as decrypting a piece of information is called cryptography.6 It is also termed as the Science of secret writing. It can be summed up as the study of techniques for preventing access to sensitive data by parties who are not authorized to access the data. It is a technique that allows a piece of Information to be converted into cryptic form before being stored in the computer database or transmitted over an insecure network.

• B.    Private Key Cryptography

This type of cryptography follows a procedure of sharing a single key between the sender and the receiver. If the key is disclosed, then the system is said to be compromised. Such a system does not prevent the receiver from forging a message from the sender. It is also called Symmetric Key cryptography. 2

• C.    Public Key Cryptography

This type of cryptography comprises of two different keys-a public key for encryption and a private key for decryption. The decoding function is extremely difficult to compute without knowing the private key. It is also called Asymmetric Key cryptography. 2

• D.    Cipher

The encrypted form of the plain text or original content of the information that is finally transmitted is the cipher.

• E.    Plain Text

The original message or content of the information that is to be transmitted is the plain text. A key is further applied on it to create a cipher.

• F.    Encryption

It is the transformation of data into a form in which it cannot be made sense of without the use of some key. ³

The process of generation of the cipher based on that key is called encryption.

• G.    Decryption

The retrieval or decoding of the original message from a cipher by using some function is called decryption. In this process, the cipher is transformed back to the plain text at the receiver’s end for which the plain text was intended to.

• H.    Cryptosystem

A computer program used in transforming a plain text to cipher and vice versa in a key-dependent and unpredictable manner is called a cryptosystem. 4

• I.    Intruder

A person who is not authorized to access the information or the network. The most important aspect of cryptography is to secure the confidential information from reaching people with unauthorized access to a network in a manner where the retrieved information by an intruder will make no sense.

• III.    Using Public-Key Cryptosystems To Transfer Messages Secretly

In a public key cryptosystem, each participant is assigned a pair of inverse keys E and D. Different functions are used for enciphering and deciphering, one of the two keys can be made public, provided that it is impossible to generate one key from the other. E can be made public, but D is kept secret. The normal transmission between senders and receivers can be replaced by an open directory of enciphering keys, containing the keys E for all participants.

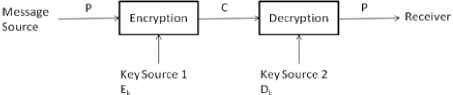
Fig. 1. Flow of message from the sender to receiver.

When a person A wishes to send a message to a person C, the enciphering key is used to generate the cipher text. There can be a person B who can intrude and have unauthorized access to the message. There is always a chance that the information is no more secret and runs the chances of being tampered with. Since, the enciphering key is available, B can try and encipher a message and send it to C instead of the original cipher that was send by the sender. However, only the deciphering key of C can decipher the original message and any kind of tampered irrelevant information can be ignored because of the same. Even digital signatures find a way into security in context of Public-key systems. The following shows the usage of Public-key Systems to implement Digital Signatures.

Here, A signs m by computing,

C = D A (m)                 (1)

B validates A’s signature by checking,

E A (C) = m                  (2)

Disputes can be judged by checking whether E A (C) restores m in the same way as B. Precisely,

D K (E K (m)) = E K (D K (m)) = m        (3)

The secrecy and authenticity in a Public-key System has been a concern for the modern day cryptographic minds and the above notes for the basic concept hidden behind the maintenance of the same while developing a Public-key Cryptographic System. 5

• IV.    Related Works

Cryptography is the one that gives a right way to secure the data while in transmission. In today’s computer world, various encryption algorithms are available.10 Ciphering existed ever since the days of Caesar to the ruling of Napoleon to the furious days of 2nd World War with Enigma and it has been an uphill since then. Our paper deals with significant works of data encryption of recent times and deduces a new technique keeping a note on the usage and performances of the others that we have come across. Methods like Rijndael’s Algorithm, Probabilistic Random Number Generation, Percon8 algorithm, Pseudo Random Number generation provides quite a clear picture of using random numbers in data encryption. But the generation of an entire random sequence for each of the 95 printable characters is something that has lacked in the above methods. The Brute force algorithm for breaking the cipher can take a toll with the huge number of possibilities for deciphering a particular character. The recent interests in Chaos Theory shifts our interests to entropic conditions thus favoring the usage of Random numbers. The plan is always to generate a robust cipher so that Brute force attacks can be resisted more.

The Rijndael algorithm used in “ A New Approach for Encryption Method using Collective Techniques with Rijngdael Algorithm ” that takes random number for each and every character. Random key value is different for every message. The mentioned work implements the security level through various stages. In this paper, the algorithm is categorized into three stages. On each stage an intermediate cipher text is produced at the process end. In this encryption algorithm two intermediate ciphers are produced at first process, final cipher text is resulted at the third process. The given algorithm has long bits of encrypted data even for the small input message. For example, 8 bits character input message gives minimum of 24 bits character encrypted data. Rijndael of AES algorithm is involved to substitute each plain text into another character by using salt values. The salt values changes or mix up with the plain text characters to produces lengthy altered characters. ¹⁰

Now, we take a look at the works mentioned in “Percon8 Algorithm for Random Number Generation”, which was published in May 2014. PERCON8 is named so as its uses Permutation-Concatenation to generate 8 Random Numbers in one Round. PERCON8 Algorithm combines the advantages of Mid Square Random Number Generation technique (4 digit input) and Linear Congruential Generator (m=32) while exploiting their limitations to its use. It is a multi-round algorithm that can be used for generation of Random Numbers. The numbers of rounds are not fixed, that is, they depend on the values of seed that are used as inputs in every round, until the seed becomes zero. Each round generates a sequence of eight 8- digit Random Numbers. As the technique employs Linear Congruential Generator which produces serially correlated Random Numbers, a Permutation Matrix is used to decorrelate the sequence thereby rendering the estimation nearly impossible.11

The Multiplier using encoder technique of “ ECC ENCRYPTION SYSTEM USING ENCODED MULTIPLIER AND VEDIC MATHEMATICS ” by Bonifus PL and Dani George of Multiplier Using Encoder Technique for encoding has been taken into consideration. This Vedic Mathematics technique defines the concept of how one can obtain the product of two numbers without actually multiplying them just by generating the partial products of the binary equivalents of the respected numbers and adding them up after shifting of bytes. The technique may not be devised for actual multiplication but for is an hideous tool for encoding. The concept about the given technique has been explained in details in the next section.

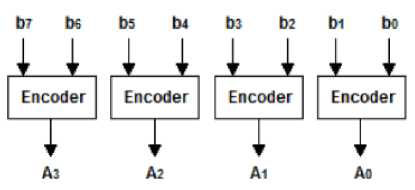
Fig. 2. Grouping Bits using Encoder.

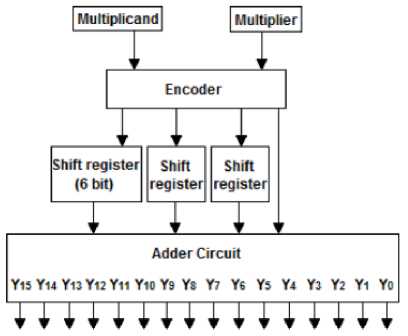
Fig. 3. Encoded Multiplier Architecture for 8 bit Multiplier.

• V.    Latest Method

• A.    Multiplier Using Encoder

While considering a recent encoding technique based upon Multiplier using an encoded algorithm, we have achieved a significant way of hiding text by means of generating partial products. The number of partial products generated in this method are half compared to Vedic and conventional methods. For 8 bit multiplier, the number of partial products required will be 4. We have used this fact to encrypt any piece of text which holds characters having UNICODE values less than equal to 128 or in a precise way, 8-bit character equivalents in binary system. We obtain the final cipher by considering 2 characters at a time and by considering the fact that the UNICODE values are supposed to be multiplied and hence we obtain 4 partial products from this. The partial products are generated based upon the UNICODE value of the second character and calculated with respect to 2 bits at a time from the tail of the 8 bit binary equivalent. We generate the cipher by means of the 4 partial products in a haphazard manner along with the first character’s UNICODE value and continue this step until all the characters of the plain text are converted to the desired output. The obtained cipher is send to the receiver. While deciphering, each partial product is then organized in the proper sequence. The partial products in the second, third and fourth placed partial product are altered a bit in the following manner:

• 1)    The decimal equivalent of the 2^nd placed partial product is multiplied by 4.

• 2)    The decimal equivalent of the 3rd placed partial product is multiplied by 16.

• 3)    The decimal equivalent of the 4th placed partial product is multiplied by 64.

The calculated values are then added up along with the decimal equivalent of the 1st placed partial product and then it is divided by the first character’s UNICODE value which was also present in the cipher. The obtained result is the second character’s UNICODE value. The cycle of this decrypting event continues until the entire cipher text is broken and then the obtained values are arranged and represented as characters thus producing the original message. 1

• B.    Encoding Algorithm

• 1)  If A_i is 0 then partial product P_i is 0.

• 2)  If A_i is 1 then partial product P_i is the multiplicand.

• 3)    If A_i is 2 then partial product P_i is obtained by shifting the multiplicand one bit left.

• 4)    If A i is 3 then partial product P i is the sum of partial products of A i for i = 1 and 2.

• C.    Encoding Steps

• 1)  Group the multiplier into 2 bits each starting from

the LSB.

• 2)    Find the value of A_i from the encoder table.

• 3)    Find the partial products based on the value of A i .

• 4)    Partial products are given to the adder circuit with a shift of one bit, two bit, four bit, six bit one by one.

• 5)    The adder circuit gives the final product.

Length of Plain Text	Time taken for encrypting (in secs.)	Time taken for decrypting (in secs.)
5	0.0083	0.002
39	0.046	0.0161
45	0.051	0.02
10	0.0028	0.0045
43	0.0328	0.0191
25	0.014	0.012
26	0.015	0.012
25	0.014	0.013
23	0.0145	0.0117
95	0.1553	0.0716
6	0.0079	0.0022
40	0.0424	0.0165
55	0.061	0.029
36	0.025	0.015

Fig. 4 Screenshot of Vedic Multiplier Implementation.

The last two steps mentioned above are used during decryption of the cipher. This technique was implemented for creating ciphers and deciphering them back by means of sending the partial products as cipher and deciphering by means of using the adder circuit to retrieve a value and then evaluate the partial products to obtain two characters at a time and the implemented program is recorded to be running well whose screenshot(Fig.1) and Time of Encryption and Decryption(Table 1) are provided.

• D.    Test Cases

  The test cases used above involve different kinds of texts comprising of all sorts of characters. Texts like, “We are up with 15$ for the #WORLD Cup 2015.” phone numbers, only non digit characters, etc. have been used for observing the time taken by the system. The record with 95 plain text characters refers to the test case where

we have used all the printable characters from the keyboard and observed the time taken for encrypting and decrypting the entire text. The retrieval of the original message was successfully achieved in all the cases.

• VI. Present Technique

The proposed system takes into account a random number generation theory for every individual message and later involves the vedic multiplier technique as the hash key. We have carefully replaced the usage of the UNICODE sequence with a controlled generation of random equivalents for each character with respect to each individual message. The given system can have a huge role to play in interoffice communications where certain messages are supposed to be made confidential and shared privately. The presence of a secured line for performing such a conversation can make it the most secured way possible to transmit a secret piece of information from one destination to the other. Even if the message is known to some intruder then the regeneration of a similar kind of tampered message is impossible because guessing the exact random sequence without the text (conversation) and time is next to impossible. Next we go through the steps and techniques involved in the generation of the random numbers, encrypting a plain text and finally decrypting it at the receiver’s end.

• A.    Random Number Generation

The uniqueness of this technique initiates with the generation of a random number sequence which is assigned to each printable character. We already have had random number generation techniques involved with other algorithms but generating a complete sequence on the basis of text and time has not been the methodology behind generating a random number. The generation takes place on the basis of a conversation between the sender and receiver which is treated as a text and the length of the text added with the occurrence of a particular character decides the order of generation of the random numbers. The particular character is chosen on the basis of the starting time of call (conversation) where the added value of the digits in the seconds place decides the position of the character to be picked. The calculated added value of occurrence of character and the length is now added with the second’s value of the time of call to give a final result. The process repeats itself until there is a value for each printable character. Limitations can be indicated with the fact that diversification among the sequence comes with a larger text conversation and further more if the textual conversation carries a wider range of characters. This process steps away from the dependency only on time and it is avoided as the generation is based on a text (conversation) as well as time.

• 1)    Algorithm for random numbers :

Step 1) Start.

Step 2) Declare lr, jr, cr, ir as integer; fr, A[95] as

String

Step 3) Input text(conversation) and time of call.

Step 4) Calculate length of text and store in lr.

Step 5) Add the first digit of seconds place to lr. Step6) Calculate the character whose number of occurrence is needed as fr and let the number of occurrence be cr.

Step 7) fr=(digit 1 of second + digit 2 of second)th position of text.

Step 8) Calculate cr on the basis of fr.

Step 9) cr=cr+lr

Step 10) Assign a value to each index of A[].

Repeat Steps until ir=95

Jr=jr+cr

If jr>95 then

Jr = jr modulus 94

End if

If A[jr] != NULL

Increment jr until a[jr]!=NULL

If jr>95 then

Jr=0

End if

End if

A[jr]=ir

Step 11) Display array A with the random equivalents.

Step 12) Stop.

• B.    Encryption Technique

We use the encoded multiplier technique mentioned above to encrypt any piece of text which holds characters having random number equivalents or in a precise way, 8-bit character equivalents in binary system. The random equivalents of each character have been considered here instead of the UNICODE values that we saw earlier. We obtain the final cipher by considering 2 characters at a time and by considering the fact that the random values are supposed to be multiplied and hence we obtain 4 partial products from this. The partial products so obtained and calculated with respect to 2 bits at a time from the tail of the 8 bit binary equivalent. We generate the cipher by means of the 4 partial products in a haphazard manner along with the first character’s random equivalent and continue this step until all the characters of the plain text are converted to the desired output. The obtained cipher is send to the receiver.

Therefore,

C = E(R(P))                 (1)

where, C is the cipher, E is the encoded multiplier key, R depicts the conversion of the characters to their random equivalents and P refers to Plain Text.

• 1)    Algorithm for encrypting plain text:

Step 1) Start.

Step 2) Declare a[],i,u as integer; b[], p[], p1[] as long; cipher as string.

Step 3) Input character by character of plain text and store the random equivalent values in a[]. Increment i by 1 for every character.

Step 4) Check the length, l of plain text, If l is odd then

A[i]=random equivalent for “ “ i=i+1

Step 5) Convert each element in a[] into its binary value and store it in b[].

Step 6) Repeat until j=(i-1)

p[0]=0

p[1]=b[j]

p[2]=b[j]*10 // binary shift by 1 position.

p[3]=p[1]+p[2]  // binary addition k=0

Repeat until k<4

u=b[j+1] Modulus 100 if u=0 then p1[k]=p[0]

else if u=1 then p1[k]=p[1]

if u=10 then p1[k]=p[2]

else if u=11 then p1[k]=p[3] end if k=k+1

b[j+1]=b[j+1]\100

cipher=cipher + p1[3] + “ “ + p1[1] +

“ “ + p1[0] + “ “ + p1[2] + “ “ + p[1] j=j+2

Step 7) cipher variable holds the cipher text.

Step 8) Stop.

• C.    Decryption Technique

While deciphering, each partial product is then organized in the proper sequence. The partial products in the second, third and fourth placed partial product are altered a bit in the following manner:

• 1)    The decimal equivalent of the 2^nd placed partial product is multiplied by 4.

• 2)    The decimal equivalent of the 3rd placed partial product is multiplied by 16.

• 3)    The decimal equivalent of the 4th placed partial product is multiplied by 64.

The calculated values are then added up along with the decimal equivalent of the 1st placed partial product and then it is divided by the first character’s random equivalent which was also present in the cipher. The obtained result is the second character’s random equivalent. The cycle of this decrypting event continues until the entire cipher text is broken and then the obtained values are arranged and represented as characters thus producing the original message.

• 1)    Algorithm for decrypting plain text:

Step 1) Start.

Step 2) Declare j=0, i=1, a[], p[], l as integer; b[] as long.

Step 3) Input cipher text.

Step 5) Repeat until i=j

Convert b[i] binary value to its decimal equivalent and Store in a[i].

Step 6) l=0

Step 7) Repeat until i=(j-1) a[i]=a[i]+a[i+2] a[i+2]=a[i]-a[i+2] a[i]=a[i]-a[i-2] a[i+2]=a[i+2]+a[i+3] a[i+3]=a[i+2]-a[i+3] a[i+2]=a[i+2]-a[i-3] a[i+1]=a[i+1]*4 a[i+2]=a[i+2]*16 a[i+3]=a[i+3]*64 p[l]=a[i+4] l=l+1 p[l]=(a[i]+a[i+1]+a[i+2]+a[i+3])/a[i+4] l=l+1 i=i+5

Step 8) Check the character equivalents for all values of p[l] sequentially to obtain the plain text.

Step 9) Stop.

Any intruder can try and understand the key used for encrypting the text and hence can tamper with the data but the presence of a random number sequence for every individual message makes it almost impossible to generate a perfect tampered data without the availability of the system itself.

• VII.    Complexity Analysis

An essential aspect to data structures is algorithms. An algorithm states explicitly how the data will be manipulated.9 Some algorithms are more efficient than others and are stated so upon some complexity analysis. Time complexity analysis is often taken as the necessary tool for evaluating the efficiency of an algorithm. By this analysis, each line of code is evaluated on the basis of the number of times that line of code getting executed. After evaluating each loop and conditional statements, we can compare the complexity between two different algorithms. In the similar fashion, the analysis of our entire technique was performed. We achieved a complexity of O(n) for our algorithms used for generating random numbers, encryption and decryption and the facts behind the same are elaborated as follows:

• A.    Random Number Generation

We tend to obtain a complexity of O(n) while generating the controlled sequence of random numbers. The chances for the complexity to climb to O(n2) is declined with the presence of a simple fact that the worst case scenario is known and it never exceeds 94 due to the usage of 95 printable characters over and over again. The actual complexity is a multiple of n + sum of all the single line statements outside any loop which we ignore and consider only n. The values from 0 to 94 are used over again and again until there is a random equivalent for each character.

• B.    Encryption

Encrypting a text in this technique involves a nested loop but consists of an inner loop which executes for a maximum number of 4 times thus making the whole algorithm follow a O(n) complexity for its execution. The other single line statements are present but the main focus stays on the unknown structure which is limited down to n in this case. Thus making this encryption well accepted for implementation.

• C.    Decryption

For limiting the breaking process to an n numbered structure, modifications were made on the implemented program and thus to the algorithm and in due course the answer to the deciphering process was also limited to a complexity of O(n). The other single line statements are present but the main focus stays on the unknown structure which is limited down to n in this case. This too continues to be feasible for implementation.

• VIII.    Conclusion

The two most fluctuating notions of our civilization is taken into account before generating the random number sequence-time and human word. On the funny note they offer much chaotic random occurrences possible making this system unpredictable for an intruder. We have also seen a number of newly used techniques and algorithms and how this technique is unique offers a new dimension for encryption and decryption of a secret and confidential message. The difference between the latest method and the proposed method is nothing but the usage of a random number sequence which enhances the robustness of the algorithm. Even if the cipher is compromised by the channel and an intruder gets hold of the cipher, brute force is expected to break it after evaluating a huge number of combinations, thus making the proposed system more secured. Achieving a complexity of O(n) also ensures that this algorithm is well acceptable for implementation. The inclusion of individual random numbers for each individual message makes it more secure in comparison to previous methods. The involvement of the already implemented encoded multiplier technique gives it another level of security. This system certainly can be an asset for any interoffice communication protocol where intruders from inside the organization can be restricted from tampering with private and confidential messages. As we started by mentioning about better and effective cryptosystems, we have successfully achieved and implemented the concept of the technique that we have mentioned here. The tabular results provided above are the test cases of the implemented system. This system thus offers a better platform for securing communication between a designated sender and receiver. The ultimate fact remains that, a key is safe as long as it is not broken and we have tried to develop a new key which can be used in securing the transmission of data as long as it cannot be broken but the Brute Attack will take much longer time to break the key for a particular message that has been encrypted using our system. Thus, making it safer in comparison to many other techniques and algorithms.