An Ensemble of Adaptive Neuro-Fuzzy Kohonen Networks for Online Data Stream Fuzzy Clustering
Автор: Zhengbing Hu, Yevgeniy V. Bodyanskiy, Oleksii K. Tyshchenko, Olena O. Boiko
Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs
Статья в выпуске: 5 vol.8, 2016 года.
Бесплатный доступ
A new approach to data stream clustering with the help of an ensemble of adaptive neuro-fuzzy systems is proposed. The proposed ensemble is formed with adaptive neuro-fuzzy self-organizing Kohonen maps in a parallel processing mode. Their learning procedure is carried out with different parameters that define a nature of cluster borders' blurriness. Clusters' quality is estimated in an online mode with the help of a modified partition coefficient which is calculated in a recurrent form. A final result is chosen by the best neuro-fuzzy self-organizing Kohonen map.
Computational Intelligence, Data Stream Processing, Neuro-Fuzzy System, Fuzzy Clustering, Machine Learning
Короткий адрес: https://sciup.org/15014862
IDR: 15014862
Текст научной статьи An Ensemble of Adaptive Neuro-Fuzzy Kohonen Networks for Online Data Stream Fuzzy Clustering
Published Online May 2016 in MECS DOI: 10.5815/ijmecs.2016.05.02
Multidimensional data clustering is common in Data Mining tasks. Such application areas as Text Mining and Web Mining have become really widespread lately. A traditional approach to solving this sort of tasks assumes that each vector of a processed sequence may only belong to a single class. Although it’s a more natural case when each specific observation may be attributed to several classes at the same time with different membership levels.
This situation is a subject under study for fuzzy cluster analysis [1, 2]. In this approach, the most effective and simplest methods are probabilistic fuzzy clustering procedures based on optimization of some objective functions. Initial data for a fuzzy clustering problem is a sample of observations which consists of N ( m x i ) - dimensional feature vectors
X = {x(1),x(2),...,x(k),...x(N)}cRn , and a result of this clustering procedure is a partition of the initial data set into m overlapping classes with some membership levels 0 < Uj (k) < 1 of the k - th feature vector to the j- th cluster, j = 1,2,...,m . Thus, the overwhelming majority of the well-known fuzzy clustering algorithms is designated for a batch mode processing which means that a sample volume N can’t be changed while the data are processed.
There’s a wide class of tasks to be solved only with the help of the Data Stream Mining [3-16] approach when data are fed and processed in an online mode. This task is rather typical for Web Mining when information is fed in a real time mode directly from the Internet.
Self-organizing maps (SOMs) by Kohonen proved its efficiency in clustering tasks. Their efficiency is defined by their computational simplicity and their ability to work in a real time mode for sequential data processing. These neural networks are learnt with the help of self-learning procedures based on the principles “Winner takes all” (WTA) and “Winner takes more” (WTM). It’s previously assumed that a structure of processed data implies that formed clusters don’t mutually intersect which means that it’s possible to build a separating hyper-surface which clearly distinguish different classes during a learning procedure of a neural network.
Recurrent modifications of the fuzzy clustering algorithms (which make it possible to solve a task in an online mode) were introduced for sequential data processing in [17, 18]. It should be noted that the introduced procedures are structurally close to the Kohonen self-learning rule according to the principle «Winner Takes More». It allows introducing a so-called «fuzzy clustering Kohonen network» [19] which possesses a number of advantages comparing to a conventional self-organizing map.
The well-known and most commonly used fuzzy clustering algorithms can’t be called fuzzy in the full sense, because their results are significantly defined by a value of a special parameter (also known as a fuzzifier в which is chosen empirically). A case when в belongs to an interval from 1 to ^ corresponds to a transition from crisp borders (в ^ 1), which are obtained with the help of the K-means procedure, to their complete blurriness (в ^”), when all observations belong to all clusters with the same membership level. We should note that в = 2 in most cases that corresponds to the fuzzy C-means procedure (FCM) by Bezdek [20].
There may be a situation while processing real-world data when one object belongs to different classes at the same time and these classes mutually intersect (overlap). Conventional SOMs don’t take into consideration this occasion, but this problem can be considered with the help of fuzzy clustering techniques.
The remainder of this paper is organized as follows: Section 2 describes fuzzy clustering techniques with a variable fuzzifier. Section 3 describes an ensemble’s architecture of adaptive neuro-fuzzy Kohonen networks. Section 4 gives some details on possibilistic fuzzy clustering with a variable fuzzifier. Section 5 presents a real-world application to be solved with the help of the proposed fuzzy clustering approach. Conclusions and future work are given in the final section.
-
II. Fuzzy Clustering with a Variable Fuzzifier
Algorithms based on goal functions are considered to be strict from a mathematical point of view among all clustering procedures. They solve a task of their optimization under different a priori assumptions. The most commonly used procedure in this situation is the probabilistic approach which is based on a goal function’s minimization
Nm
E (Uj, Cj ) = ZZ -в( k )||* (k)-Cj|| under constraints
m
Zu(k) = 1,( j=1
N
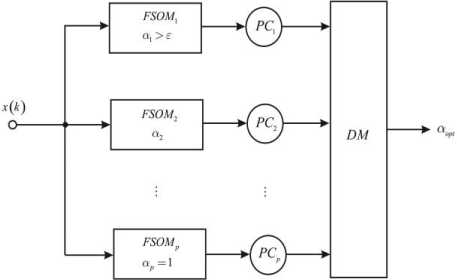
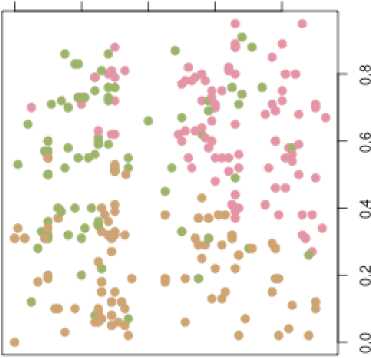
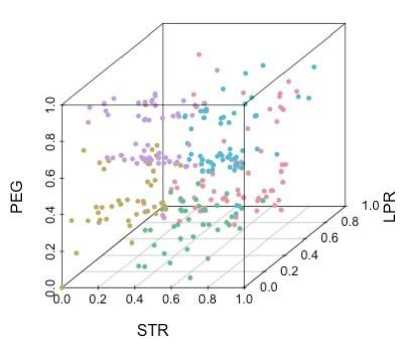
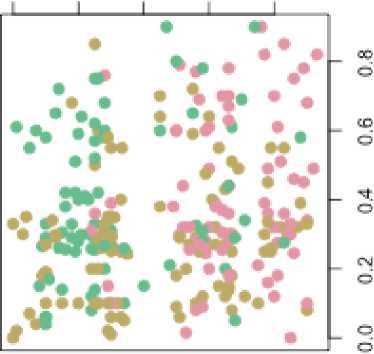
0 k=1 where и (k)e[0,1] is a membership level of a vector x(k) to the j -th class, c is a prototype of the j -th cluster, в is a non-negative fuzzification parameter (a fuzzifier) which actually determines a level of borders’ blurriness between clusters, k = 1,2,...,N. A result of this clustering procedure is a (N x m) -matrix и = {Uj(k)} which is also called a fuzzy partition matrix. We should notice that elements of the matrix U due to the constraint (2) may be considered as probabilities that data vectors belong to some definite clusters. Because of this fact, procedures based on the minimization (1) are called probabilistic fuzzy clustering algorithms. A number of clusters m is set beforehand and can’t be changed during computation procedures. Introducing the Lagrange function Nm L(и, (k),Cj,Л(к)) = ZZuв (k)||*(k)-J + «=1j =1 ( A (4) N_ . 1 +Z2(k )| ZU( k )-11 (here Л(k) is an undetermined Lagrange multiplier) and solving the Karush-Kuhn-Tucker system of equations, we can get a solution in the form (I * (k)-cl1)1-в Z2.(1 *(k)-с,Г • Z "j k)*(k) Z U' k) 2( k ) = - ( о1-в - o\-в [р II *(k)-c,l ] which coincides with the Fuzzy C-Means algorithm (FCM) by J.Bezdek (when в = 2). And when в ^ 1 its results are close to results of the well-known conventional crisp clustering algorithm (Hard K-Means, HKM). As an alternative to procedures that use a fuzzifier 1 < в<” , Klawonn and Hoeppner [21] offered an objective function for fuzzy probabilistic clustering Nm E ( u , с )=ZZ (au2(k)+(1 - a) uj(k)) I * (k)- cj II (6) k=1 j=1 with the constraints (2) and (3), where 0 < a< 1 is an adjustable parameter which defines a nature of the obtained solution. Introducing the Lagrange function L(и, (k),с,,2(k)) = Nm = ZZ(auj2 (k) + (1 - a ) UJ(k) )| I* ( k )-Cj II + k=1 ,=1 . Л m-^ 1 +Z 2(k )| Z uj( k)-11 and solving the Karush-Kuhn-Tucker system of equations dL (Uj (k), Cj, Л( k)) dUj (k) = (2aUj (k) +1 - a )||x (k)- cy || + Я( k) = 0, V CL ( Uj(k), j A(k )) = = -E 2 (au,2(k ) + (1 - a) u (k))( x (k )-c, ) = 0, k=1 dL(Uj (k),Cj,A(k)) 6A( k) m E uj( k)-1 = 0, j=1 we come to a solution uj(k )=- - a ---+ 2a 1 - a 1 + m---- _______2a у m ||x(k2-CjL El=11 x (k)-Cll Г _ E N. i(“u2( k) + (1 - a) Uj (k)) x (k) j EN.i(au2(k) + (1 - a)Uj (k)) . в , but there are currently no formal rules how to choose it and to tune it. Therefore, while solving a concrete task in a batch mode, this task is usually repeatedly solved with the help of the expression (7) with different a values (from a very small quantity to 1). It’s clear that such an approach can’t solve tasks effectively in an online mode. It might be expedient to use an idea of an ensemble of parallel working clustering procedures [23, 24] in this situation, where each clustering procedure works with a different from others a value. This ensemble can be easily implemented with the help of adaptive neuro-fuzzy Kohonen networks [25]. They are two-layer architectures where prototypes are clarified in the Kohonen competitive layer (which contains m neurons NK ) and membership levels are calculated in the output layer (which contains m neurons NM ). There is an architecture of the two-layer adaptive neuro-fuzzy Kohonen network in Fig.1. There is also an ensemble formed by such networks in Fig.2. A self-learning algorithm for the p - th ensemble’s member (p = 1,2,...,q) in an ensemble that contains q neuro-fuzzy networks can be written down in the form It’s easy to notice that when a = 1 this procedure coincides with FCM. Thus, the procedure (7) can’t be used for solving Data Stream Mining tasks, because it can’t process information in an online mode. Therefore, an adaptive modification of the expression (7) was introduced in [22] 1 - a u. (k +1) =-- 2a 1 - a 1 + m---- 2a 2, Cj(k+1)=Cj(k)+ Em l=1 || x (k +1)-c(k )||2 (8) + n(k)(au2 (k +1) + (1 - a)uy (k + 1))x x( x (k +1)- Cj(k)) Fig.1. An adaptive neuro-fuzzy Kohonen network (FSOM) where n(k) is a learning rate parameter. It’s easy to notice that the second recurrent expression (8) is the Kohonen self-learning rule according to the principle «Winner Takes More» with a neighborhood function auJ (k +1) + (1 - a ) Uj (k +1) . Although a value of the parameter a in the formulas (7) and (8) lies in a much narrower range than a fuzzifier Fig.2. An architecture of an ensemble of adaptive neuro-fuzzy Kohonen networks cpp(k+1) = cjp(k)+ +n(k)(a-“- (k) + (1 - ap)“j- (k))x x( x ( к + 1)-Cjp(к)), < , x 1 - ap “j-(k+1) =— "O + 1 + m 1-0 +___________2a-______ m ||x (к + 1)- cj- (кf 1=1||x (к + 1)- c- (к)||2 where in the Kohonen layer is tuned with the help of the first ratio (9), and the output layer calculates membership levels ujp (k +1) for each incoming observation x (k +1). Classification quality provided by each ensemble member may be estimated with the help of any fuzzy clustering index [2]. Wherein one of the simplest and most effective indexes is the so-called “partition coefficient” (PC) which is a mean value of squared membership levels of all observations to each cluster: 1 k+1 m PC- (k+1)=gg “ 2- T ). (10) This coefficient has a clear physical sense: the better clusters are expressed, the higher the value PC is (a limit is pc = 1), its minimum (PCp = m-1) is reached if data belong to all clusters evenly. But this phenomenon is obviously a worthless solution. This coefficient is convenient in the framework of the proposed system, because it allows online calculation. It should be noticed that the expression (10) is closely related to the traditional FCM. This coefficient must be modified for a considered case in the form k+1 m PC-(k+1)=^gg(a-“2- (t)+(1- a-) “j- (t )) which coincides with the expression (10) when ap= 1. So, clustering a data stream that is fed in an online mode is solved with the help of parallel working adaptive neuro-fuzzy Kohonen networks which differ from each other only by a value of the parameter ap . Thus, the network’s results are applied to a maximum value PCp (k +1) as a final result at any particular time point. must be equal to 1). That’s why algorithms that use the constraint (2) are called probabilistic fuzzy clustering algorithms. An existence of this constraint leads to the fact that an observation which doesn’t belong to any class gets the same membership levels for all classes. One can avoid this drawback if the ideas of possibilistic fuzzy clustering are used [26]. These ideas are based on minimization of an objective function Nm E (“j,C) = gg “f(k) I x (k)- cj II + k=1 l=1 m N P +gPj g(1 - “j( k)) j=1 k=1 where a scalar parameter ^ > 0 defines a distance where a membership level takes on a value of 0.5 which means that if ||x (k)- cj| f = ^j then “j (k) = 0.5. Introducing an objective function [22, 25] similarly to (6) Nm E (“j, Cj) = gg (a“2 (k) + (1 — a) “j (k)) | x (k) - Cj || + k=1 j=1 mN 2 +g ^j-g(a (1-“j(k))) j=1 k=1 and minimizing it by “, cy, ^ , we come to a modified possibilistic procedure in the form “j (k) = (a«j +(1—a )||x (k)—cj ||2)+pj 2a (||x(k)- cj||2 + pj) < c = g N=1(a“2( k )+(1 - a) “j(k))x (k) (11) j g N=1 (a“2( k )+(1 - a) “j(k)) , g N=1(a“ j2 (k )+(1 - a) “j( k ))l Iх (k)- cj f g N=1 (a“2 (k)+(1 - a) “j( k)) Basic problems that arise in fuzzy clustering have to do with constraints on a sum of membership values (they It’s interesting to note that this ratio for a prototype calculation in the formulas (7) and (11) completely coincides. The expressions (11) can be written down for an adaptive case in the form U (k +1) = (aMj(k)+ (1- «)|x(к +1) - cj(к)||2)+Mj(k) 2a (|x(k +1)- Cj (k)|| + m (k)) Cj (k +1) = Cj (k) + n(k)(au,2(k +1) + (1 — a)u, (k + 1))x ^^ x(x(k +1)-Cj (k)), M(k +1) = (Z‘ =1 (auj(P) + (1 -a)uj(P))x x|x(p)-cj(k+1)||2)x x(Sk=1(au2(p)+(1 -a)uj(p))) . As one can see, the second recurrent ratio (12) is the WTM self-learning rule by Kohonen with the neighborhood function au2 (k + 1) + (1-a) Uj (k + 1). Although the possibilistic algorithm (12) is a little more complicated from a computational point of view than the probabilistic procedure (8), its advantage is the fact that new clusters may be detected with the help of the possibilistic approach during online data processing. If a membership level of a new incoming observation x(k +1) to all classes turns out to be lower than some predefined threshold then we can assume that there’s a new (m +1)- th cluster and its initial prototype coordinates are cm+1 (0) = x ( k + 1). The algorithm (12) can be used as a learning procedure for the two-layer FSOM (Fig.1). Let’s notice that an ensemble of clustering neural networks with the help of the possibilistic approach was introduced in [27, 28], but its unwieldiness impedes its usage while processing data streams. Simplicity of the ensemble’s (Fig.2) numerical implementation makes it possible to process data in a real time mode. We chose 3 attributes (STR, LPR, PEG) for the sake of visualization. 0.0 0.2 0.4 0.6 0.8 Fig.3. The Result of Fuzzy Clustering (STR/PEG) Fig.4. The Result of Fuzzy Clustering (PEG/ STR/LPR) As it can be seen, the proposed method makes it possible to represent clusters in a rather compact form. A level of cluster overlapping is rather high (and it will We have taken real-world data for our experiment. A data set describes students’ knowledge status about the subject of Computer Science. The data set contains multivariate characteristics. It contains 302 instances with 5 attributes for each observation. Speaking of attribute information, the data set contains these attributes: - STG (a degree of study time for goal object materials); - SCG (a degree of a user’s repetition number for goal object materials); - STR (a degree of user’s study time for related objects with a goal object); - LPR (a user’s exam performance for related objects with a goal object); - PEG (a user’s exam performance for goal objects). Fig.5. The Result of Fuzzy Clustering (SCG/PEG) keep on growing when a feature vector’s dimensionality increases). An a parameter for the considered case belonged to an interval [0.3; 0.4]. As it can be seen from Fig.3, there are 3 fuzzy clusters. Generally speaking, students’ current knowledge level should be determined with the help of real values (STG, SCG, PEG, STR, LPR). It should be noted that there are some points in Fig.3 which are not likely to be in those regions. For example, a point belongs to a “green” class although all neighbor points in that region belong to some other (“pink” or “yellow”) class. Probably, this fact means that a student didn’t actually spend much time on his exam preparation although he demonstrated a high level of performance (his PEG index is high). There may be another situation when a student spent much time on his preparation but his results aren’t very good. So, the clustering accuracy increases for fuzzy algorithms and worsens for crisp ones with the growth of a sample size; the clustering accuracy lessens with the growth of dimensionality of a feature space. Fuzzy procedures are preferable for those clustering tasks when every object belongs to several categories at the same time. The method for online fuzzy clustering multidimensional data sequences to be processed in a real time mode is proposed. The task is solved with the help of an ensemble of adaptive neuro-fuzzy Kohonen networks which differ from each other by a parameter’s value that accounts for fuzziness of the received results. The proposed procedure has rather simple computational implementation and makes it possible to organize parallel computing to accelerate the system’s processing speed (because it can process data in an online mode and this fact is really important for Web Mining and Data Stream Mining). The results may be successfully used in a wide class of Data Stream Mining, Dynamic Data Mining, Temporal Data Mining tasks and especially in such applied areas as Web Mining, Text Mining, Medical Data Mining etc. So, the proposed ensemble of adaptive neuro-fuzzy self-organizing Kohonen maps has proved its efficiency for online Data Stream fuzzy clustering. A number of experiments demonstrated a high effectiveness of the proposed neuro-fuzzy system especially under conditions of clusters’ overlapping. The authors would like to thank anonymous reviewers for their careful reading of this paper and for their helpful comments. This scientific work was supported by RAMECS and CCNU16A02015. [1] F. Hoeppner, F. Klawonn, R. Kruse, and T. Runkler, Fuzzy Clustering Analysis: Methods for Classification, Data Analysis and Image Recognition, Chichester: John Wiley & Sons, 1999. [2] R. Xu and D.C. Wunsch, Clustering (IEEE Press Series on Computational Intelligence), Hoboken: John Wiley & Sons, 2009. [3] H. Bouchachia and E. Balaguer-Ballester, “DELA: A Dynamic Online Ensemble Learning Algorithm”, in Proc. 22nd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN 2014), Apr. 2014, pp. 491-496. [4] D. Leite, P. Costa Jr., and F. Gomide, “Evolving granular neural networks from fuzzy data streams”, Neural Networks, vol. 38, 2013, pp. 1-16. [5] D. Leite, R. Ballini, Pyramo Costa Jr., and F. Gomide, “Evolving fuzzy granular modeling from nonstationary fuzzy data streams”, Evolving Systems, vol.3(2), 2012, pp. 65-79. [6] D. Leite, R. Ballini, Pyramo Costa Jr., and F. Gomide, “Evolving fuzzy granular modeling from nonstationary fuzzy data streams”, Evolving Systems, vol.3(2), 2012, pp. 65-79. [7] D. Kangin and P. Angelov, “Evolving clustering, classification and regression with TEDA”, in Proc. International Joint Conference on Neural Networks (IJCNN 2015), July 2015, pp. 1-8. [8] R. Hyde and P. Angelov, “A new online clustering approach for data in arbitrary shaped clusters”, in Proc. International Conference on Cybernetics (CYBCONF 2015), June 2015, pp. 228-233. [9] R.D. Baruah, P.P. Angelov, and D. Baruah, “Dynamically evolving clustering for data streams”, in Proc. Evolving and Adaptive Intelligent Systems (EAIS 2014), June 2014, pp. 1-6. [10] R. Rosa, F.A.C. Gomide, D. Dovzan, I. Skrjanc, “Evolving neural network with extreme learning for system modeling”, in Proc. Evolving and Adaptive Intelligent Systems (EAIS 2014), June 2014, pp. 1-7. [11] D. Dovzan and I. Skrjanc, “Recursive clustering based on a Gustafson-Kessel algorithm”, Evolving Systems, vol. 2(1), 2011, pp. 15-24. [12] R.D. Baruah, P.P. Angelov, and D. Baruah, “Dynamically evolving fuzzy classifier for real-time classification of data streams”, in Proc. IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE 2014), July 2014, pp. 383-389. [13] R.D. Baruah and P.P. Angelov, “Online learning and prediction of data streams using dynamically evolving fuzzy approach”, in Proc. IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE 2013), July 2013, pp. 1-8. [14] A.P. Lemos, W.M. Caminhas, and F.A.C. Gomide, “Multivariable Gaussian Evolving Fuzzy Modeling System”, IEEE Trans. Fuzzy Systems, vol.19(1), 2011, pp. 91-104. [15] R.D. Baruah and P.P. Angelov, “Evolving fuzzy systems for data streams: a survey”, Data Mining and Knowledge Discovery, vol.1(6), 2011, pp. 461-476. [16] M. Pratama, S.G. Anavatti, M.J. Er, and E. Lughofer, “pClass: An Effective Classifier for Streaming Examples”, IEEE Trans. Fuzzy Systems, vol.23(2), 2015, pp. 369-386. [17] Ye. Bodyanskiy, V. Kolodyaznhiy, and A. Stephan, “Recursive fuzzy clustering algorithms”, in Proc. 10th East West Fuzzy Colloqium, Sept. 2002, pp. 276-283. [18] Ye. Bodyanskiy, “Computational intelligence techniques for data analysis”, Lecture Notes in Informatics, vol. P-72, 2005, pp. 15-36. [19] Ye. Gorshkov, V. Kolodyazhniy, and Ye. Bodyanskiy, “New recursive learning algorithms for fuzzy Kohonen clustering network”, in Proc. 17th Int. Workshop on Nonlinear Dynamics of Electronic Systems, June 2009, pp. 58-61. [20] J.C. Bezdek, Pattern Recognition with Fuzzy Objective Function Algorithms, N.Y.: Plenum Press, 1981. [21] F. Klawonn and F. Hoeppner, “What is fuzzy about fuzzy clustering? Understanding and improving the concept of the fuzzifier”, Lecture Notes in Computer Science, vol. 2811, 2003, pp. 254-264. [22] B. Kolchygin and Ye. Bodyanskiy, “Adaptive fuzzy clustering with a variable fuzzifier”, Cybernetics and System Analysis, vol. 49, no. 3, 2013, pp.176-181. [23] A. Topchy, B. Minaei-Bidgali, A.K. Jain, and W.F. Punch, “Adaptive clustering ensembles”, in Proc.17th Int. Conf. on Pattern Recognition “ICPR 2004”, Aug. 2004, pp. 272 – 275. [24] S. Vega-Pons and J. Ruiz-Shulcloper, “A survey of clustering ensemble algorithms”, Int. J. Pattern Recognition and Artificial Intelligence, vol. 25, no. 337, 2011, pp. 337-372. [25] Ye. Bodyanskiy, B. Kolchygin, and I. Pliss, “Adaptive neuro-fuzzy Kohonen network with variable fuzzifier”, Int. J. Information Theories and Applications, vol. 18, no. 3, 2011, pp. 215-223. [26] R. Krishnapuram and J.M. Keller, “A possibilistic approach to clustering”, Fuzzy Systems, vol. 1, no. 2, pp. 98-110. [27] B.V. Kolchygin, “Ensemble of neuro-fuzzy Kohonen networks for adaptive clustering”, in Proc. 2nd Int. Sci. Conf. of Students and Young Scientists “Theoretical and Applied Aspects of Cybernetics”, Nov. 2012, pp. 176-181. [28] Ye.V. Bodyanskiy, V.V. Volkova, and A.S. Yegorov, “Clustering of document collections based on the adaptive self-organizing neural network”, Radio Electronics,Informatics, Control, vol.1 (20), 2009, pp. 113-117. Science and Technology Applications, Artificial Intelligence, Network Security, Communications, Data Processing, Cloud Computing, Education Technology. Prof. Bodyanskiy is the professor of Artificial Intelligence Department at KhNURE, the Head of Control Systems Research Laboratory at KhNURE. He has more than 600 scientific publications including 40 inventions and 10 monographs. His research interests are Hybrid Systems of Computational Intelligence: adaptive, neuro-, wavelet-, neo-fuzzy-, real-time systems that have to do with control, identification, and forecasting, clustering, diagnostics and fault detection. Prof. Bodyanskiy is an IEEE Senior Member and a member of 4 scientific and 7 editorial boards. Oleksii Tyshchenko graduated from Kharkiv National University of Radio Electronics in 2008. He got his PhD in Computer Science in 2013. He is currently working as a Senior Researcher at Control Systems Research Laboratory, Kharkiv National University of Radio Electronics. His current research interests are Evolving, Reservoir and Cascade Neuro-Fuzzy Systems; Computational Intelligence; Machine Learning. Olena Boiko graduated from Kharkiv National University of Radio Electronics in 2011. She is a PhD student in Computer Science at Kharkiv National University of Radio Electronics. Her current interests are Time Series Forecasting, Fuzzy Clustering, Evolving Neuro-Fuzzy Systems.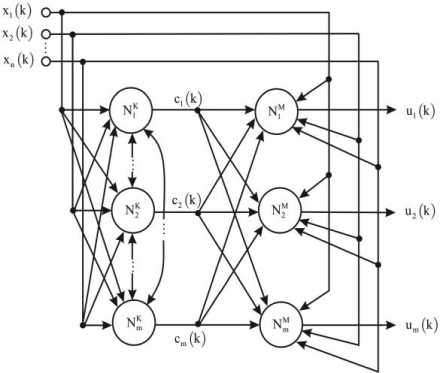
IV. Possibilistic Fuzzy Clustering with a Variable Fuzzifier
VI. Conclusion



Список литературы An Ensemble of Adaptive Neuro-Fuzzy Kohonen Networks for Online Data Stream Fuzzy Clustering
- F. Hoeppner, F. Klawonn, R. Kruse, and T. Runkler, Fuzzy Clustering Analysis: Methods for Classification, Data Analysis and Image Recognition, Chichester: John Wiley & Sons, 1999.
- R. Xu and D.C. Wunsch, Clustering (IEEE Press Series on Computational Intelligence), Hoboken: John Wiley & Sons, 2009.
- H. Bouchachia and E. Balaguer-Ballester, "DELA: A Dynamic Online Ensemble Learning Algorithm", in Proc. 22nd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN 2014), Apr. 2014, pp. 491-496.
- D. Leite, P. Costa Jr., and F. Gomide, "Evolving granular neural networks from fuzzy data streams", Neural Networks, vol. 38, 2013, pp. 1-16.
- D. Leite, R. Ballini, Pyramo Costa Jr., and F. Gomide, "Evolving fuzzy granular modeling from nonstationary fuzzy data streams", Evolving Systems, vol.3(2), 2012, pp. 65-79.
- D. Leite, R. Ballini, Pyramo Costa Jr., and F. Gomide, "Evolving fuzzy granular modeling from nonstationary fuzzy data streams", Evolving Systems, vol.3(2), 2012, pp. 65-79.
- D. Kangin and P. Angelov, "Evolving clustering, classification and regression with TEDA", in Proc. International Joint Conference on Neural Networks (IJCNN 2015), July 2015, pp. 1-8.
- R. Hyde and P. Angelov, "A new online clustering approach for data in arbitrary shaped clusters", in Proc. International Conference on Cybernetics (CYBCONF 2015), June 2015, pp. 228-233.
- R.D. Baruah, P.P. Angelov, and D. Baruah, "Dynamically evolving clustering for data streams", in Proc. Evolving and Adaptive Intelligent Systems (EAIS 2014), June 2014, pp. 1-6.
- R. Rosa, F.A.C. Gomide, D. Dovzan, I. Skrjanc, "Evolving neural network with extreme learning for system modeling", in Proc. Evolving and Adaptive Intelligent Systems (EAIS 2014), June 2014, pp. 1-7.
- D. Dovzan and I. Skrjanc, "Recursive clustering based on a Gustafson-Kessel algorithm", Evolving Systems, vol. 2(1), 2011, pp. 15-24.
- R.D. Baruah, P.P. Angelov, and D. Baruah, "Dynamically evolving fuzzy classifier for real-time classification of data streams", in Proc. IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE 2014), July 2014, pp. 383-389.
- R.D. Baruah and P.P. Angelov, "Online learning and prediction of data streams using dynamically evolving fuzzy approach", in Proc. IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE 2013), July 2013, pp. 1-8.
- A.P. Lemos, W.M. Caminhas, and F.A.C. Gomide, "Multivariable Gaussian Evolving Fuzzy Modeling System", IEEE Trans. Fuzzy Systems, vol.19(1), 2011, pp. 91-104.
- R.D. Baruah and P.P. Angelov, "Evolving fuzzy systems for data streams: a survey", Data Mining and Knowledge Discovery, vol.1(6), 2011, pp. 461-476.
- M. Pratama, S.G. Anavatti, M.J. Er, and E. Lughofer, "pClass: An Effective Classifier for Streaming Examples", IEEE Trans. Fuzzy Systems, vol.23(2), 2015, pp. 369-386.
- Ye. Bodyanskiy, V. Kolodyaznhiy, and A. Stephan, "Recursive fuzzy clustering algorithms", in Proc. 10th East West Fuzzy Colloqium, Sept. 2002, pp. 276-283.
- Ye. Bodyanskiy, "Computational intelligence techniques for data analysis", Lecture Notes in Informatics, vol. P-72, 2005, pp. 15-36.
- Ye. Gorshkov, V. Kolodyazhniy, and Ye. Bodyanskiy, "New recursive learning algorithms for fuzzy Kohonen clustering network", in Proc. 17th Int. Workshop on Nonlinear Dynamics of Electronic Systems, June 2009, pp. 58-61.
- J.C. Bezdek, Pattern Recognition with Fuzzy Objective Function Algorithms, N.Y.: Plenum Press, 1981.
- F. Klawonn and F. Hoeppner, "What is fuzzy about fuzzy clustering? Understanding and improving the concept of the fuzzifier", Lecture Notes in Computer Science, vol. 2811, 2003, pp. 254-264.
- B. Kolchygin and Ye. Bodyanskiy, "Adaptive fuzzy clustering with a variable fuzzifier", Cybernetics and System Analysis, vol. 49, no. 3, 2013, pp.176-181.
- A. Topchy, B. Minaei-Bidgali, A.K. Jain, and W.F. Punch, "Adaptive clustering ensembles", in Proc.17th Int. Conf. on Pattern Recognition "ICPR 2004", Aug. 2004, pp. 272 – 275.
- S. Vega-Pons and J. Ruiz-Shulcloper, "A survey of clustering ensemble algorithms", Int. J. Pattern Recognition and Artificial Intelligence, vol. 25, no. 337, 2011, pp. 337-372.
- Ye. Bodyanskiy, B. Kolchygin, and I. Pliss, "Adaptive neuro-fuzzy Kohonen network with variable fuzzifier", Int. J. Information Theories and Applications, vol. 18, no. 3, 2011, pp. 215-223.
- R. Krishnapuram and J.M. Keller, "A possibilistic approach to clustering", Fuzzy Systems, vol. 1, no. 2, pp. 98-110.
- B.V. Kolchygin, "Ensemble of neuro-fuzzy Kohonen networks for adaptive clustering", in Proc. 2nd Int. Sci. Conf. of Students and Young Scientists "Theoretical and Applied Aspects of Cybernetics", Nov. 2012, pp. 176-181.
- Ye.V. Bodyanskiy, V.V. Volkova, and A.S. Yegorov, "Clustering of document collections based on the adaptive self-organizing neural network", Radio Electronics, Informatics, Control, vol.1 (20), 2009, pp. 113-117.


