An evolutionary model for selecting relevant textual features

Published Online November 2018 in MECS DOI: 10.5815/ijmecs.2018.11.06

Arabic is one of the most used languages in the world, however so far there are only few studies looking for textual information in Arabic. It is considered as a difficult language to deal in the field of processing automatic language, considering its morphological and syntactic properties [25]. Faced with these failures, we propose a new approach based on word distribution and their semantic power.

Many studies have shown that the enormous power of written or oral words lies in their meanings. Words trigger concepts, ideas, memories, situations, circumstances, and feelings that are related to our internal memory [3].

The power of words rightly chosen is very great, whether those words are used to inform, to entertain, or to defend clearly and concisely a point of view. They create a powerful vibratory field that will attract the circumstances and objects that one wants to have if the desire behind these words is strong enough [2].

Dialogue is not simply an interaction of words, but there are both actions and reactions, because in each pronounced sentence there may be cooperation, resistance, or negotiation between words meanings, resulting in mutual influence and learning. Although the words of a text are as influential on their immediate neighbors as on distant neighbors, one must not forget that the reaction always depends on the subject who receives these words. It is for this reason that the speaker tries to express her/his idea and her/his thought by a set of words sharing the same context or the same concept, we cannot isolate the words of their temporal and spatial contexts which give them their meaning and power [1].

Our objective in this work is to determine a semantic proximity calculation process between the words of a corpus based on a theoretical model of the theory of evolution that mimics human altruistic behavior.

We’ve defined a new selection criterion called altruistic semantic measure that seeks to explore the distributional hypothesis that words in similar contexts tend to have similar meanings [24]. A directed graph was used to characterize a probability distribution of words and their proximity is evaluated by a semantic distance from the neighbors.

• II.    The Theory of Evolution

Group Selection or Multiple Level Selection (MLS) is a generalization of Darwin's theory of evolution by natural selection, a generalization of Ronald Aylmer Fisher's natural selection theorem1. Darwin's theory is a special case of the group selection where selection pressure only applies to individuals. This theory, in its current version, was developed in 1970 by the American biologist George Price2 and published in Nature.

• A.    The Price Equation

Let P be a population of n individuals in which a particular characteristic varies. These n individuals can be grouped by the value of the characteristic that each one presents. In this case, there are at most n groups of distinct values of this characteristic and at least a group of a single value of the considered characteristic. Let's index each group by i, the number of individuals in each group by n and the value of the characteristic shared by all members of the group by z . Now let us posit that for any value of the characteristic is associated in a selective value to such as n, = to n , n' is the number of descendants of the group i to the next generation.

Since all the descendants of the group i have a parent that can come from another group, the average value of the characteristic of the descendants z ^, can be different.

Note the variation in the mean value of the characteristic of group i by A z_t defined by:

def

A z i = z i - Z i                (1)

Now let z be the mean value of the characteristic in the population P and z' this same value in the next generation. Define the change in the average value of the characteristic by:

def

A z = z ^, - z                (2)

Note that this is not the average value of A z . Also, let to be the mean selective value of the population. Price's equation functionally links these variables as follows:

to A z = cov( to , z ) + E ( to A zi ) (3)

The functions cov and E are respectively the mathematical expectation and the covariance of the probability theory. Assuming that to is non-zero, it is often convenient to write it in the following form:

₌ covU ^.z ) ₊ E ^{( to} i ^Az, ) to            to

The first term of Price's equation can be interpreted as the “intergroup” selection pressure and the second term as the “intra group” selection pressure. In a simplified way, it may be convenient to consider intergroup selection as equivalent to group selection and intra-group selection to individual selection. On the other hand, some mechanisms such as reciprocal altruism or parental selection affecting the intra-group component can be seen as group selection, while the geographic separation of groups, affecting the intergroup component, can be interpreted as kin selection. Considering kinship selection as a special case of Price's equation applied to altruism is the most accurate mathematical approach.

• B.    Price's Altruistic Model

If the kin selection makes it possible to explain how the family groups appear, it makes it difficult to explain the formation of the multifamily groups and even less the groups of anonymous members. The problem lies in the fact that in Hamilton's equation, altruism is directly related to genetic distance, with no apparent connection, no altruism. George Price had the idea of reusing the notion of altruism of the Hamilton equation and applying it to its generalization of Fisher's fundamental theorem of natural selection. His model is as follows:

to = k — az_t + bz             (5)

With:

to : The selective value of the individual i;

k : The selective value proper of any individual of the group (the same for all to simplify the calculations);

az : The selective loss of value of the individual i in altruism towards the group, z is the altruism of the individual i;

bz : The selective value gain generated by the altruism of the group towards any individual of the group (here towards the individual i), z is the average altruism of the z_i .

After derivation using Price's equation (by putting the coefficients and larger than zero), we obtain:

to A z = - a var(z_i )             (6)

With:

to : The new average selective value of the population after a step of evolution (one generation);

A z : The difference between the new medium altruism and that of the previous generation;

var(z ) : t he population altruism variance of the previous generation.

This result means that for altruism to persist in a population, it is imperative to be uniform (variance of zero). In the opposite case, the evolution will converge towards the lowest level of altruism.

Therefore, if we stop the reasoning here, we could conclude that altruism can’t exist in nature and this even in a highly related population, even for clones. Never could any altruistic behavior emerge, if only from herding instinct.

• C.    Price's Complete Model

Now suppose that the population is divided into a set of groups indexed by i and that each group is composed of individuals indexed by j. Each individual is therefore identified by two indices, i and j. By taking the model of Price we get:

toy = k — az у + bz_t            (7)

With:

to : The selective value of the individual ij. ij k : The selective value proper of any individual of the population (the same for all to simplify the calculations).

az : The selective loss of value of the individual ij in ij altruism towards the group i, z is the altruism of the individual ij.

bz : The selective value gain generated by the altruism of the group i towards any individual of the group i (here towards the individual ij), z is the average altruism of zij .

After derivation using the complete Price equation (by putting the coefficients a and b larger than zero), we obtain:

A z = cov( to-/to , z ) + E ( to Az, to )        (8)

Here, the first term indicates the selective advantage of the groups to have altruistic members; the second term is the loss of the individual selective advantage of the group members resulting from their altruisms.

Considering that altruism is non-uniform in the group and that the second term is negative, the first term becomes:

A z = ( b — a ) var( z ) + E ( to A z_t / to )     (9)

Here, unlike the “divisionless” model in groups, the variance propels the growth of altruism as long as the gain in altruism towards the group offsets the individual losses. As a result, the intergroup component is larger if the genetic disparity between groups is high; this consequence is comparable to the kin selection and this one can thus be regarded as a theorem of the group selection of Price.

By posing the evolution of the stabilized average altruism, i.e. A z = 0 , we obtain:

( a — b ) var( z ) = E ( to A z_t to )    (10)

By considering the evolution of the stabilized average altruism of each group, i.e. A z_t = 0 , we obtain:

( a — b )var( z ) = 0 (11)

Therefore, the evolution mechanism is stabilized if all group members have the same level of altruism (zero variance) or the gain in altruism towards the group perfectly offsets the individual losses (a = b). If instead of altruism we had studied malevolence among members of different groups, we would have come to a similar conclusion: the evolution mechanism stabilizes if all group members have the same level of malice towards the members of the other groups or that the gain in malevolence towards the other groups compensates perfectly the individual losses.

• III. THE Altruistic Model for Selecting Relevant Textual Features

• A.    Main Aims

The goal is to gain a better understanding of the group selection method in response to certain numbers of attribute selection problems that any massive data processing system can confront.

Taking into account this flexibility of Price’s model and the philosophical approach of informational interaction between the linguistic units of a natural language, we try to elaborate a generic model of information extraction from a corpus.

• B.    Steps of the Proposed System

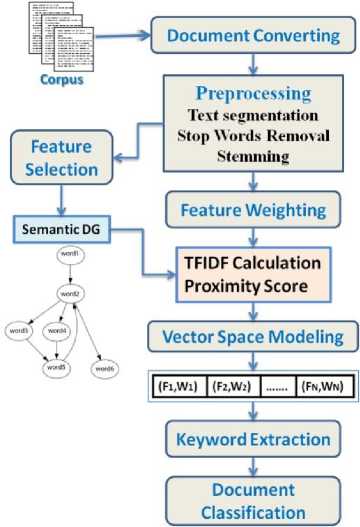
Semantic DG

Corpus

Feature Selection

Preprocessing Text segmentation Stop Words Removal Stemming

Vector Space Modeling

TFIDF Calculation Proximity Score

Document Classification

■ * Document Converting

Feature Weighting

Keyword Extraction

Fig.1. The architecture of text classification process

We extended Price’s model by adapting the TFIDF calculation for information evaluation and retrieval to identify relevant concepts that best represent a document.

The model combines several measures in order to model the semantic similarity of words. These measures are: TFIDF, RBF functions, oriented graphs and semantic altruism.

• C.    Preprocessing and Documents Converting Phases

The preprocessing phase consists of applying to the entire text a noise filtering (stopwords elimination , punctuation, date) in the first place, a morphological analysis (lemmatization, stemming) in the second place and filtering of extracted terms in the third place. This treatment is necessary due to changes in the way that the text can be represented in Arabic. The preparation of the text includes the following steps:

• •    Convert text files in UTF-16 encoding.

• •    Elimination of punctuation marks, diacritics and non-letters and stopwords.

• •    Standardization of the Arabic text, this step is to transform some characters in standard form as ‘ J ,' )’ to ‘I’ and ‘^ ,^’ to ‘^’ and ‘j’ to ‘j’.

Stemming the remaining terms is performed using the Khoja stemmer [4] for Arabic documents.

• D.    Features extraction

• 1)    TFIDF Weighting

Used in the vector model, the TFIDF (term frequency -inverse document frequency) is a statistical measure for assessing the importance of a word in a document, relatively to a documents collection or a corpus [23]. The weight increases proportionally with number of word occurrences in the document. It varies also according to the word frequency in the corpus. There are many variants of TF - IDF [5, 6, 21].

The basic data of this formula are f(d,t) which is the term frequency t in document d and df (t) which is the number of documents having at least one occurrence of the term t, the latter aims at giving greater weight to the less frequent words, which are considered most discriminating. The functions TF reflect a growing monotony and IDF a decreasing monotony.

• a)    Problems

In the TF schema, the importance of a term t is proportional to its frequency in the document. This improves the recall but not always the precision, terms that are common are not discriminating that often leads to remove the most frequent terms: but what is the limit?

In the IDF schema, the words which appear in few documents are interesting and relevant. This scheme is intended to improve the accuracy.

• b)    Solution

Salton [22] has shown that the best results were obtained by multiplying TF and IDF. Finally, the weight is obtained by multiplying the two measures:

fW (t, d) = tf(t, d) x log( n)   I ^tf 2( t, d) x log2( n)

n_t t                        n_t

n is the number of documents in the collection. n t is the number of documents containing the term t.

• 2)    Directed Semantic Graph

Semantic networks were originally designed as a model of human memory [7]. A semantic network is a labeled graph (more precisely a multigraph). An arc binds (at least) a start node to (at least) one arrival node. Relations between nodes are semantic relations and relations of part-of, cause-effect, parent-child, etc.

The concepts are represented as nodes and relationships in the form of arcs. The links of different types can be mixed as well as concepts and instances. In our system, we used the concept of semantic network as a tool for strengthening of semantic graph outcome from the extracted terms of learning documents to improve the quality and representation of knowledge related to each theme of the document database.

The construction of semantic graph takes into account the order of extraction and distribution of the terms in the document. Each term is associated with a radial basis function which determines the proximity to some vicinity (area of semantic influence of the term). We have adapted our system to support any kind of semantic relationship.

Such an approach allows to shape the semantic altruism relations supposedly existing between terms, and therefore, there will be a strong chance that the terms may have larger selection coefficients.

Suppose that a given document contains the sequences of the following words:

وفق کونجرس امريكي أمس خمس جرأ زود سقف قرض امريكي بقع مليار دولار

Fig.3. Pretreatment Step

وافق الکونجرس الامريكي امس الخمیس على اجراء لزيادة سقف الاقتراض الامريكي بواقع 290 مليار دولار

Fig.2. Original text

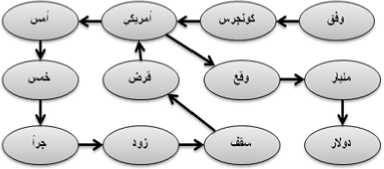
Fig.4. From processed text to graph construction.

• 3)    The Radial Basis Proximity

The discriminating function g of RBF proximity with one output is defined by the distance between the input form of each prototype and the linear combination of the corresponding radial basis functions data [8, 9]:

N

g ( x ) = ω ₀ + ∑ ω _i ϕ ( d ( x , x_i ))      (13)

i =1

While d(x,x i ) is the distance between the input x and the support x i ,{ ω , ω ,..., ω } are the combination weights and ϕ the radial basis function.

The modeling of RBF fuzzy proximity is both discriminating and intrinsic. Indeed the layer of radial basic functions corresponds to an intrinsic description of the training data, then the output combination layer seeks to discriminate different classes.

Indeed, one of the greatest advantages of this method lies in its applicability in almost any dimension (whence its versatility) because there are generally little restrictions on the way the data are prescribed [11].

For applications it is indeed desirable that there are few conditions on the geometry or the directions in which the data points have to be placed in space. No triangulations of the data points or the like are required for radial basis function algorithms, whereas for instance finite element [12, 13]; or multivariate spline methods normally need triangulations [11, 14]. In fact, the advance structuring of the data that some other approximation schemes depend on can be prohibitively expensive to compute in applications, especially in more than two dimensions. Therefore, our approximations here are considered as meshfree approximations, also for instance to be used to facilitate the numerical solution of partial differential equations [15].

E. Price's Model Adapted to Textual Characteristics Extraction

Using Price's formula for natural selection, and by imitation, we try to study the semantic proximity relations between words by a distributional analysis in order to highlight the semantic altruistic behavior of words. This new adaptation, highlights the pressure of selection between groups and intragroup. In a simplified way, it tries, on the one hand, to group the elements that have similar altruistic semantic properties, and on the other hand to separate the too different groups in terms of semantic altruism. Now suppose that the population is divided into a set of groups indexed by i and that each group is composed of individuals indexed by j. Each individual is therefore identified by two indices, i and j. By taking the model of Price we get:

ω = k - az + bz           (14)

With:

ω : The selective value of the element ij. ij

1) The Proper Selective Value k

It is the proper selective value of every element of the population. To simplify the calculations, this value is the same for all (the selection coefficient). Here we take the maximum selective value. It is calculated from the semantic graph as follows:

2) The Absolute Selective Value

Number of descendents ^ab^{s =} Number of parents

^NOutgoing nodes             (15)

= _N

Incoming nodes

3) The Relative Selective Value

^ω rel ⁼

ωabs max{ωabs , i∈{1...N}}

max{ ω  } is the maximum value of all absolute values

^ω abs ^.

4) t he selection coefficient z

S = 1 - ω rel             (17)

5) The selective loss of value az : The selective loss of value of the element ij in ij semantic altruism towards the group i, z being the altruism of the element ij, it is the TFIDF.

By choosing to evaluate the selective values dispersion of the neighboring elements relative to the mean we have opted for two models, a Gaussian and a RBF model based on a Cauchy function and the constant can be defined as follows:

The Gaussian model

N a =ω +∑ ωϕ(ω )

i =1

ϕ ( ω _i ) =

2 π

ω i ²

e

with:

ω : The weighting of the central element (core)

ω : The weights of the immediate neighbors of the central element in the point cloud ( tfidf ).

- The RBF model based on a Cauchy function

N a =ω0 + ∑ωiϕ(d(x, xi))         (20)

i = 1

ϕ (d(x, x_i )) =      ¹

1 + d(x, x )

d(x, x ) : The minimum distance separating the central element x and its immediate neighbors x i , calculated from the graph by a Breadth First Search algorithm (BFS).

• 6)    The selective gain in value

bz : The selective value gain generated by the altruism of the group i towards any individual of the group i (here towards the individual ij ), z is the mean semantic altruism of the z ( tfidf ) and b is the selective value average.

After derivation using the complete Price equation (by putting the coefficients a and b larger than zero), we obtain:

Nz = cov(o [о, Z;) + E (о kz; J

The first term indicates the selective advantage of the groups to have altruistic semantic elements; the second refers to the loss of the individual selective advantage of the group elements as a consequence of their semantic altruisms.

• IV. Application Results

Table 1. Performance of different classifiers on the feature set

Features Selection Method	Category	Classification score TFIDF
		KNN	KDtreeKNN	Naive Bayes
RBF-Gaussian model	Sport	0.5746	0.8313	0.6813
	Politic	0.7413	0.9813	0.36
	Economy	0.7186	0.8166	0.6733
RBF-Cauchy Model with selection coefficient	Sport	0.5726	0.8313	0.6806
	Politic	0.7373	0.9806	0.3586
	Economy	0.7126	0.8146	0.6726

Table 2. Clustering performance on the feature set

Features Selection Method	Detected classes	SOM (Self-Organizing Map) TFIDF
		Sum Of Squared Errors
RBF-Gaussian model	3	2.96
RBF-Cauchy Model with selection coefficient	3	2.82

Our extraction and classification algorithm uses several relevant parameters: the connectivity of the oriented graph of semantic altruism, the minimal distance between points (vertices), an RBF model combining the preceding parameters and the statistical measures to calculate the density of points to be in a radius (neighborhood) so that these points are considered relevant. The input parameters are therefore an estimate of the density of documents terms.

To measure the performance and evaluate the relevance of the proposed model, we choose to test two types of classification algorithms (supervised and unsupervised) of the java-mlplatform [16] on a corpus of

5000 Arabic documents uploaded to the Aljazeera website (www.aljazeera. net).

The basic idea of the algorithm is then, for a given word, to recover its neighborhood and to calculate its selection coefficient and its weighting. This word is then considered as one of the most important terms. We then go through the neighborhood step by step to find all the words that are semantically close to it.

At first, for an automatic classification phase, we have opted for self-adaptive maps (SOM), or Kohonen's maps [17] which take advantage of neighborhood relations to realize a discretization in a very short time. It is assumed that space does not consist of isolated areas, but of compact subsets. So by moving a reference vector to a zone, we can say that there are probably other zones in the same direction that must be represented by reference vectors. This justifies the fact of moving the neurons close to the winner in the grid in the same direction, with smaller amplitude of displacement. The algorithm presents simple operations; it is therefore very light in terms of calculations cost.

The neighborhood in auto adaptive maps is unfortunately fixed, and a link between neurons cannot be broken even to better represent discontinuous data. Growing Cell Structure or Growing Neural Gas is the solution to this problem. Neurons and links between neurons can be removed or added when the need arises. Many measures are used to evaluate the cluster performance, we cite Sum of Squared Errors [18].

In the context of the classification we have chosen the naive Bayesian classifier which, despite its extremely simplistic basic assumptions, has demonstrated more than sufficient efficiency in many complex real situations. In 2004, an article showed that there are theoretical reasons behind this unexpected effectiveness [19]. The nearest-k method and the KDTreeKNN (Approximate k-NN search using KD-trees [20]. This algorithm requires knowing k, the number of neighbors to consider. A classic method for having this value is cross validation (CV).

The performance of the classifier is returned as a measure of performance. A Performance Measure is a wrapper around the values for the true positive, true negative, false positive and false negative. This method also provides a number of methods for calculating a measure of aggregate measures such as accuracy, f-score, recall, precision, etc.

• V.    Conclusion

The preceding tables present the classification experimental results that we obtained on an Arabic corpus. The semantic proximity between words must be highlighted when we deal with complex documents like Arabic ones. For this purpose, it is essential to broaden our reflection on the representation of models to the nature of our resources. By refining statistical analysis and enriching the distributional data, we try to come up with more interesting and relevant semantic interpretations.

We have chosen to apply statistical measure TFIDF which is reference in this domain. Then, we have developed a system for Arabic contextual classification, based on the semantic altruism vicinity of terms and the use of a radial basis modeling. This new statistical model is based on a calculation of the concept of semantic altruism, which represent best a document. The obtained results are promising and open up interesting prospects. But the stemmer remains a burden for the processing of a complex language such as Arabic, it diminishes performance. However, given the flexibility of the model, the addition of parameters such as lexical inclusion, morpho-lexical, morpho-syntactic indices, as well as an adaptation of the model to the different datasets could improve the results.