An Identity-based Blind Signature Approach for E-voting System

Published Online October 2017 in MECS DOI: 10.5815/ijmecs.2017.10.06

An election is a basic right for the people in democratic countries e.g. India, U.S., Australia, etc., that allows people to articulate their views to the government. The traditional way of voting, also called ballot paper based voting system is very simple, portable, and affordable. But it has many disadvantages e.g. low participation rate of voting, time-consuming, booth capturing and low tally speed. In order to tackle aforementioned problems, Evoting system plays a lead role in the rapid development of internet technology.

Many forward-thinking countries and election commissions are adopting an electronic voting system to improve their elections. In general, an E-voting system will be ideally acceptable, if the system must ensure the following requirements [1], [2]: Voter anonymity, No- coercion, Authentication, Integrity, verifiability, Uniqueness, etc.

According to experts, E-voting system based on the cryptographic technique is categorized into three classes: blind signature [3], mix-net [4] and homomorphic encryption [5]. A blind signature is [3] one of the main tools that allow the election commission to get votes without identifying the identity of the voter. Some evoting system based on blind signature are given in [3], [6], [7], [8] and [9]. A mix-net [4] is another tool that allows the number of servers to shuffle the encrypted votes and hides the relationship between the voters and votes by performing some mathematical operations. A homomorphic encryption technique allows the election commission to counts votes without decrypting them. Based on homomorphic function, some E-voting schemes are proposed by [5], [10] and [11].

E-voting is first implemented by the David Chaum [4] using the novel idea of the blind signature scheme given by him in [12], [13]. Since blindness and Untraceability are two principle traits of the blind signature scheme so it plays a significant role in those applications where user anonymity is the main concern, for example, E-voting system, E-cash payment system [14] and E-commerce. Many blind signature based E-voting systems are given in [3], [6], [7], [8] and [9]. This schemes respect the certificate-based public key cryptosystem, therefore, gets the worst of certificate and public key management. Besides, Identity-based cryptosystem (IBC) [15] solve this overhead by mapping the user's identity to the public key that means the public key is directly derived from the user's unique identity. Later several cryptographic primitives such as Boneh's and others' identity-base encryption [16], [17] and Cha-Cheon’s identity-based signature [18] has been introduced.

Our contribution. Using the technology of IBC, blind signature scheme is first presented by Zhang et al [19]. Several blind signature schemes using identity-based cryptosystem are presented by Zhang et al. [20], [21], Huang et al. [22] and Kumar et al. [23]. Ribarski et al. in [24] suggested some Identity-based blind signature scheme for E-voting system, but they could not implement. In this sense, the objective of the paper is twofold. Firstly, we proposed a blind signature scheme using the identity-based cryptosystem which uses the combination of Boneh’s short signature scheme [25], Bolyreva’s blind signature scheme [26] and Cha-Chaon’s Identity-based signature [18]. The security is respected by the hardness of computing ECDLP problem and GDH problem. Under adaptive chosen message and ID attacks, the proposal is secure against existential forgery attack. The scheme is found suitable for E-voting system as compared with others ID-based blind signature scheme. Secondly, based on our ID-based blind signature and Garcia et al.’s scheme [3], we design a framework for Evoting scheme.

The arrangement of the article is given as: section 2 gives the preliminaries about the bilinear pairing, mathematical assumption and required security constraints. Our proposed ID-based blind signature system presented in Section 3. The security analysis and computational comparison are given in section 4. Section 5 discusses the design of E-voting system. Finally, the conclusion is shown in section 6.

• II.  Preliminaries

• A.    Elliptic curve cryptography

Suppose the elliptic curve equation y² = (x³ + mx + n)modp , where x, y ∈ F_p and ( 4m³ + 27n²)modp ≠ 0 . Formally, the Elliptic Curve is a set of points ( x, y ) which satisfied these equations and is an additive abelian group with point 0 (identity element). The condition ( 4m³ + 27n²)modp ≠ 0 tells that y² = (x³ + mx + n)modp has a finite abelian group that can be defined based on the set of points E p (m,n) on elliptic curve. Consider points A = (x A , y A ) and B = (x B , y B ) over E p (m, n ), the addition operation of elliptic curve is represented as A + B = C = (x_C, y_C), defined as following: x_C = (µ² – x_A -x_B) and y_C = (µ(x A - x C ) - y A )modp . Where µ is given in (1)

yB  yA modp,ifA Ф B xB ~ xA

3 x a + m          о

—A ---mod p , ifA = B

2 y _A

Based on elliptic curve, Neal Koblitz [27] and Victor Miller [28] introduced elliptic curve cryptosystem. It is noted that addition operation and multiplication operation in ECC are equivalent to modular multiplication and modular exponentiations in RSA respectively.

• B.    Bilinear Pairing

Suppose two cyclic groups having same order q are G₁ and G 2 with and generator of G 1 be P. A map e: G 1 X G 1 -> G 2 is a bilinear map if is fulfills the following three properties:

• 1.   Bilinearity : For every X, Y ∈ G 1 , and x, y ∈ Z q

• 2.   Non-Degeneracy : If X is a generator of G₁ then e(X,

e ( xX , yY ) = e ( X , Y ) xy         (2)

• X) is the generator of G 2 that means if there exist X ∈ G 1 such that e(X, X) ≠ 1, where 1 is the identity element of G 2 .

• 3.   Computability : There must exist an algorithm that

can efficiently compute e(X, Y) for every X, Y ∈ G 1 .

• C.    Mathematical assumption

Discrete logarithm problem on Elliptic Curve (ECDLP) . Consider Y = xX where X, Y ∈ E_p(a, b), and x ∈ Z q , it is computationally easy to compute Y from X and x but difficult to compute x from Y and X.

Decision Diffie-Hellman problem (DDH) . Given x, y, z ∈ Z q X ∈ G 1 and check if z = xy mod q.

Computational Diffie-Hellman Problem (CDH) . Given x, y ∈ Z q , X ∈ G 1 and , compute xyX.

Gap Diffie-Hellman problem (GDH) . If CDHP is hard and DDHP is hard, problem works in GDHP.

• D.    Digital Signature

  Short signature scheme. Consider the GDH problem assumption, Boneh-Lynn-Shacham [25] proposed the short signature scheme. As compared to the RSA and DSA, this scheme generates the smaller signature with the same level of security. For example, RSA and DSA generate the signature of 3072 bits and 512 bits respectively for a 128 bits level of security, while this scheme produces a signature of just 257 bits. Under the chosen message attack, the hardness of CDHP, and the collision resistant property of the hash function, security proof of short signature is respected the random oracle model.

Boldyreva blind signature. Boldyreva’s blind signature scheme [26] is based on the bilinear pairing. For signature, it requires the additive group on an elliptic curve, and for verification, it requires the multiplicative group. That means, scalar multiplication of points on an elliptic curve is the main cryptographic operation for blinding the message, signing the blinded message and unblinding the blinded signature, and the bilinear property of pairing-based cryptography to compute the DDHP is the cryptographic operation to verify the signature. Boldyreva [26] gave the security proof as similar to the Boneh short signature scheme. The security proof is based on the random oracle model. Under the chosen message attack, the hardness of CDHP, and the collision resistant property of hash function, this scheme is secure against the one more forgery attack.

Cha-Cheon Identity-Based Signature. Considering the GDH groups obtaining from bilinear pairing, Cha-Cheon [18] proposed an Identity based signature scheme. This scheme exploits the use of boneh-Franklin IBE scheme [16] and is equally efficient. Cha-Cheon in [18] proved that if group G is such that if CDHP is difficult and DDHP is easy, then his scheme is secure against existential forgery attack under chosen message attack for ID–based scheme.

• E.    Security property

An ID-based blind signature scheme is considered as secure if it fulfills the following two principle traits: Blindness and non-forgeability. The state where signer signs on message without being unable to see the content is known as blindness. Under chosen message and ID attacks, the user is unable to create one more signature is known as non-forgeability. The reader may refer [29] for more details.

Blindness: Blindness property is defined in terms of following game playing between the challenger C and PPT adversary A .

• ■    Setup : The challenger C chooses a security parameter k and executes the Setup algorithm to compute the published parameter PARAM and master key s. Challenger C sends PARAM to A .

• ■    Phasel : A selects two distinct message M 0 and M 1 and an ID i , and sends them to C .

• ■    Challenge : C uniformly chooses a random bit b £ {0, 1} and ask A for signature on M b and M 1-b . Finally, C strips both the Signatures and gives the original signatures ( o_b, o_1-b ) to A .

• ■    Response : A guesses bit b’£ {0, 1} on tuple ( M₀, M₁, O b , o j _-b ). A wins the game if b = b’ holds with probability Pr[b = b’] >1/2 +k"ⁿ.

To define the Non-forgeability, let us introduce the following game playing between the Adversary A, who act as Requester and the Challenger C, who act as honest SA.

• ■    Setup : On random Security parameter   k ,  the

challenger C execute the Setup algorithm and computes the parameter PARAM and master key s. Challenger C sends PARAM to A .

• ■    Queries : Adversary A can performs numbers of queries as follows:

• •    Hash function queries : For requested input, challenger C computes the hash function values and sends it to the attacker A .

• •    Extract queries : A selects an Identity ID and ask for S ID to A .

• •    BlindSig queries : A selects an ID and Message M , blindly requested the Signature from C. C compute signature on Message M with respect to ID .

• ■    Forgery : Game is in favor of A, if against identity

• I D*, A response with n valid Message-Signature (M 1 , σ 1 = (S’ 1 , M’ 1 , y 1 )),. (M 2 , σ 2 = (S’ 2 , M’ 2 , y 2 ))….. (M n , σ n =(S’ n , M’ n , y n )) such that

• •    Each message M i is distinct from other Message M j in given Message-Signature (M 1 , σ 1 = (S’ 1 ,

M’ 1 , y 1 )),. (M 2 , σ 2 = (S’ 2 , M’ 2 , y 2 ))….. (M n , σ n =(S’ n , M’ n , y n )) set.

• •    Adversary A is restricted to ask an extract query on Identity ID* .

• •    Execution of BlindSig algorithm is bounded by n.

Non-forgeability: An ID-based PBS scheme is break by an Adversary A ( t, q E , q B , k^-n ), if A runs no more than t , A make Extract queries no more than q E and runs BlindSig phase no more than q_B, with an advantage more than equal tot k^-n . Under the adaptive chosen message and ID attacks, our ID-based PBS scheme is said to secure against one-more forgery, if no adversary A ( t, q E , q B , k^-n )-breaks the scheme.

• III. Our Proposed ID-BS System

This section gives a blind signature scheme based on identity-based approach which is constructed on the GDH problem group.

• A.    Notation and Acronyms

Suppose,

• G 1 , G 2 : Group of points on elliptic curve.

• P: Generator of group G1.

• e: G 1 X G 1 -> G 2 : Bilinear map function.

H 1 , H 2 : Pre-image hash function, where,

H i : {0, 1} * ^ G_b

H 2 : {0, 1} * X G 1 ^ Z q

ID U , ID S : Identities of user and signer respectively.

S IDU , S IDS : Private keys of user and signer respectively.

• B.    Definition

The proposed identity-based blind signature scheme be formed with six sub-algorithms run among PKG, Signer and user, in an interleaving way, defined as follows:

• •    Setup : PKG selects randomly s ∈ Z q and gives public key as P_Pub = sP. Publishes PARAMS = {G₁, q, e, P, P_Pub, H₁, H₂}, and keep secret key s secretly.

• •    Extract : PKG computes S IDS = sQ IDS , and S IDU = sQ IDU, where Q IDS = H 1 (ID S ) and Q IDU = H 1 (ID U ), and sends S IDS and S IDU to the signer and the user respectively.

• •    Authenticating & Blinding : Using his private key, the user computes K = e(S IDU , R). Any forger could not reached to next step correctly because k + K . Then the user picks a random number a ∈ Z_q as a blinding factor, computes

A = a-1R, h = H (m, A), bM = ah,

X = H2( Ьм, K)

and sends ( b M , X) to the signer.

• •    Signing: The signer computes

X = H2(bM, k)(7)

and check if X’ == X holds. For valid justification, the signer produces a signature with his private key as

S = (r + bM )Sms, where r ∈ Zq,is random chosen integer and sends it back to the user.

• •    Unblinding: The user unblinds the blinded signature S with blinding factor a as

S ’= a - 1 S ,                    (9)

publishes signature {S’, A} on the message m.

• •    Verify : On given ( S’, A, m ), signature is valid if the following equation holds

e ( S ', P ) = e ( A + H ₂ ( m , A) Q^ )   (10)

This gives the complete model of our proposed Identity-based blind signature scheme.

• IV. Analysis of our Scheme

This section gives the analysis of our proposed scheme in terms of security and computational efficiency.

• A. Security Analysis

• Theorem 1.    Proposed ID-BS Scheme achieves the property of completeness.

Proof. Since S’ = a^-1S and h = H₂(m, A), from equation (10) the following equations verifies the correctness of our scheme.

e(S', P)

= e ( a ^{- 1} S , P )

= e ⁽ a ⁽ r + ^b M ) S IDS , ^P )

= e ⁽ a ' rQ iDS , + a ' ^b M ^Q_mss^P )

= e ( A + hQ_M , P^ )

= e ( A + H 2 ( m , A ) Q^ , Pp^ )

Hence, the correctness of our ID-BS scheme is proved. Similarly, the correctness of our ID-BS scheme can be proved for batch verification.

• Theorem 2.    Proposed ID-BS Scheme achieves the property of Blindness.

Proof. Suppose (m, S’, A) be the message-signature pair and data exchange between the user and signer be (R, b_M, S), are given to adversary A. To prove the blindness property we show that given valid signature and data exchange during one signature generation, there exists a unique blind factor integer a ∈ Z q that maps (R, b M , S) to (m, S’, A). In authenticating and blinding algorithm, the user computes A= a^-1 R with the random chosen blind factor a. So, to find the message m from the given blinded message b_M = aH₂(m, A), the signer must first find the value of a and then get the pre-image of hash function H 2 . Since H 2 is pre-image resistant and ECDLP is hard to solve in G 1 , the proposal satisfies the blindness property.

• Theorem 3.    Proposed scheme is secure against one-more signature attack (Non-forgeability).

Proof. Suppose an adversary A wants to forge a valid message-signature pair of the signer. Upon request to the challenger C for public parameter PARAMS = {G₁, G₂, P, e, q, Ppub, H 1 , H 2 }, C runs the setup algorithm and sends to A. To extract the private key corresponds to the signer identity ID S , A performs the number of queries as follows:

• •    Hash function queries : For given input ID i , C computes the hash function values Q IDi and send them to A .

• •    Extract queries : A selects an Identity ID and ask for private key S ID corresponds to ID from C. A runs Extract queries qE times (qE > 0 and is limited by the polynomial in k) using (params, ID i ) and get the corresponding S IDi where 1< i < qE.

• •    Issue queries : A selects an ID i and Message M , blindly requested the Signature from the C. C computes signature on Message M with respect to ID S .

From hash queries, if A obtains the pair (ID i , S IDSi ) such that H 1 (ID i ) = H 1 (ID S ), then the A can easily forge the valid signature on message m. Since the hash function is random oracle i.e. it uniformly generates the output, he/she cannot get any hint from queries output and could not forge the signature, shown in the followings equation:

e(S', P)

= e ( aS_f , P )

• =    e ⁽ a ( rH 2 ( t ) + b M ) S IDf , P )

• =    ^e ( ^{ar H} 2 ( t ) Q IDf , + ^ab M Q IDf , ^sP )

• =    e ( A f + hQ IDf , P pub )

• =    e ( A f + H 2 ( m , A f ) Q_mf , P_Pllb )

• ^    e ⁽ A + H 2 ( m , A ) ^Qids , P pub )

The above inequality shows that proposed ID-BS approach is secure against the non-forgeable attack.

• B. Computational Analysis

This section compares our scheme with three existing ID-based Blind signature schemes [19], [20], [22]. Table I shows the comparison of our scheme with existing scheme in terms of operations performed by the user, the signer and the verifier, where P: pairing operation, M: multiplication operation of scalar and element on G 1 , A:

addition operation of two elements on G 1 , H: hash function H: {0,1}* ^ G 1 , M s : two scalar multiplication, I s : scalar inversion, C s : comparison of two scalar, H s : hash function H_s: {0,1}*x G 2 -> Z q , E_p: exponentiation of pairing, M_p: multiplication operation on two pairing, C_p: two pairing elements comparison.

Table 1. Computational cost comparison of our scheme with other schemes

Schemes	Entities	P	M	A	H	M s	A s	I s	C s	H s	E p	M p	C p
F. Zhang et al., 2002 [19]	Signer		3	1
	User	1	3	3			1			1
	Verifier	2						1		1	1	1
	Total	3	6	5			1	1		2	1	1
F. Zhang et al., 2003 [20]	Signer		2				1
	User		3	1		2	1	1		1
	Verifier	2	1	1						1			1
	Total	2	6	2		2	2	1		2			1
Z Huang et al. 2005 [22]	Signer	1	1				1				1
	User	3	1	1	1	2					2	2
	Verifier	2			1						1	1	1
	Total	6	2	1	2	2	1				4	3	1
Our ID-BS Scheme	Signer		2			1	1		1	2
	User		2			1		1		2
	Verifier	2	1	1						1			1
	Total	2	5	1		2	1	1	1	5			1

To achieve 1024-bit RSA level security for pairingbased cryptosystem, we assume the Tate pairing defined over super-singular elliptic curve on a finite field F_q, where |q| = 512 bits [30]. Same security level for ECC based scheme, we have to use secure elliptic curve on a finite field F p , where |p| = 160 bits [30]. From [30], we assume pairing, modular exponentiation, ECC-based scalar multiplication and pairing-based scalar multiplication with running time 20.01ms, 11.20ms, 0.83ms and 6.38ms respectively. However, there are many verification tools [31] such as AVISPA, ProVerif etc. to verify the protocol. But authors gives the mathematical proof to verify the protocol given in Theorem 1.

As compared to bilinear pairing operations, ECC-based scalar multiplication, pairing-based scalar multiplication and modular exponentiation, the computation cost of hash function operation is very less. Thus, we ignored the computation cost of hash function operation. So, in order to compare performance, we just focus on the pairing operations, ECC-based scalar multiplication, pairingbased scalar multiplication and modular exponentiation.

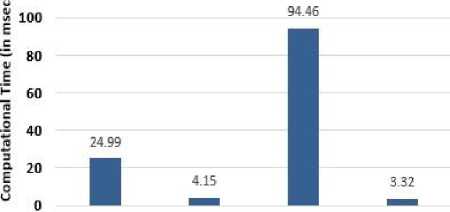
Table 2. Computational Time (in ms) comparison of our scheme with other schemes

Schemes	Computational cost (in ms)
	BlindSig	Verify	Total
F. Zhang et al., 2002 [19]	≈ 24.99	≈ 46.40	≈ 71.39
F. Zhang et al., 2003 [20]	≈ 4.15	≈ 40.85	≈ 45.00
Z Huang et al. 2005 [22]	≈ 94.46	≈ 46.40	≈ 140.86
Our proposal	≈ 3.32	≈ 40.85	≈ 44.17

Assuming the pairing operation on elliptic curve is very time taken operation, Table 1 shows that our scheme needs 2Pa + 6M +1Ms + 1Is +1Cp operations and is much efficient than [19], [20], [22] schemes, while scheme in [19]needs 3Pa + 6M + 5A + 1As + 1Is +2Hs + 1Ep + 1Mp operations, the scheme in [18] needs 2P + 6M + 2Ms + 2A + 1As + 1Is +2Hs + 1Cp operations and the scheme in [19] needs 6P + 2M + 2H + 1A + 1As + 2Ms + 1Is +4Ep + 3Mp + 1Cp operations.

From Table 2, Fig. 1(a), Fig. 1(b) and Fig 1(c), we say that our proposed scheme takes only 3.32 ms for blind signature phase, whereas[19], [20] and [22] scheme take 24.99 ms, 4.15 ms and 94.46 ms respectively. Similarly for verification phase, our scheme takes only 40.85 ms, whereas[19], [20] and [22] scheme take 46.40 ms, 40.85 ms and 46.40 ms respectively. Considering the paring operation, our scheme and [19] scheme taking less than two-third runtime of [20] scheme and one-third runtime of [22] scheme.

Blind Signature phase

Zhang et al Zhang et al Z Huang et al Our [191            (201            [22]

Identity-Based Blind Signature scheme

Fig.1(a). Computational Cost (in msec) comparison for Blind Signature Phase.

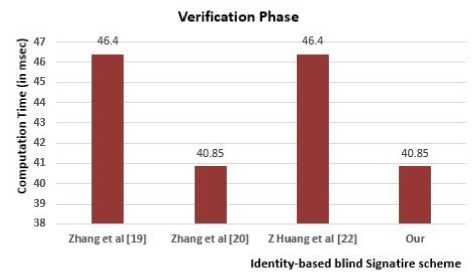
Fig. 1(b) Computational Cost (in msec) comparison for Verification Signature Phase.

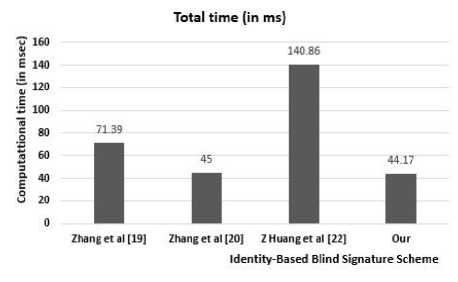
Fig. 1(c) Total Computational Cost (in msec) comparison.

• V. E-voting System

In this section, recall to our ID-based blind signature scheme, we gives a framework for an Electronic-voting system. We start with the formal definition of proposed E-voting system.

The proposed E-voting system consists of five algorithms, namely, Registration, Authentication, Vote casting, and Vote Counting, run among the following five parties, namely, Voter, Authentication Party (AP), the Vote Casting Party (VCP), Vote Tallying party (VTP) and Trusted third party (TTP). The voter must have a valid Identity ID which is uniquely identified by anyone e.g. voters ID, license, passport etc., TTP is responsible for computing and securely sending the private key for AP, VCP, and VTP with corresponding ID's. AP is responsible for authenticating the legal voters with their valid Identities, VCP is responsible for successful receiving, casting and validating the vote, and VTP is responsible for correctly counting the valid votes.

Definition (E-voting scheme) . The proposed E-voting system consists of four algorithms among the Voter, AP, VCP, VTP, and TTP, and is defined as follows:

• •    Registration . Similar to setup algorithm of our ID-based blind signature scheme, TTP computes the public parameter with his master and computes the private key for AP, VCP, and VTP with his master key by using Extract algorithm of ID-BS scheme.

Additionally, Voter and nominal candidate preregistered himself as a valid voter. A nominal list is prepared by Electoral entity contains the registered voters with their identities.

• •    Authentication . In authentication stage, voter blinds

the digital message with random blind factor and requests a blank digital ballot to the AP. In order to generate the blind signature on the blank digital ballot, the AP must first authenticate the voter, and check whether the voter is legal that means voter's name is present in the nominal list and check whether the ballot is unique that does not present previously generated. Then, the AP generates and releases a blank digital ballot to the voter using the issue algorithm of our proposed ID-based blind signature technique. The voter gets the blind signature, unblind it and produces the signature.

• •    Vote casting . The voter produces a signature on his given vote with a randomly chosen integer. An electronic ballot is generated which includes the blind signature, signature on the vote, vote and A. The electronic ballot is sent to the VCP. On receiving the ballot, the VCP checks the authenticity of A using the verification of our proposed scheme, which means, whether A is signed by the AP. Then, VCP checks the validity of authenticity of vote using Boneh's Short signature scheme. Upon successful verification of both conditions, VCP produces the hash of the concatenation of electronic ballot and the randomly chosen integer, signs it using his/her private key and sends to the voter and cache the electronic ballot for checking the vote duplicacy in future. Then Voter checks his vote by verifying the authenticity of the signature on hash.

• •    Vote counting . The VTP makes sure that there are no invalid or duplicate electronic ballots. The signature on A and vote are generated using the randomly chosen integer a so the signatures must be unique. The VTP filters the invalid voter by comparing the two ballots with their signature. If two signature in the stored list of electronic ballots is same, one vote is considered as invalid and other is valid. The VTP considered the first ballot as valid and invalidate the ballot. In order to count the valid votes, the VTP maintains the valid ballots with the receipt Rcpt in the first list and other list contains the all invalid ballots with their receipts Rcpt and published the two lists.

VI. Conclusion

The main goal of this paper is of twofold. Firstly, we proposed a blind signature scheme using the identitybased cryptosystem. Proposed scheme uses the combination of Bolyreva’s blind signature scheme [26] and Cha-Chaon’s Identity-based signature [18]. The security of our proposed system is based on the hardness of computing ECDLP problem and GDH problem which is secure against existential forgery attack under the adaptive chosen message and ID attacks. As compared to existing blind signature, proposed scheme is more efficient as it requires less number of pairing operations. Secondly, we design a framework for e-voting based on our proposed ID-BS scheme.