An Image Encryption Scheme Based on Chaotic Systems with Changeable Parameters

Published Online March 2014 in MECS DOI: 10.5815/ijcnis.2014.04.05

With the rapid development of multimedia and network technology, a bulk of digital visual data, such as digital images, video, and audio, etc. has revolutionized in the way of largely stored, manipulated, and transmitted over the Internet and wireless networks. Creative ways of storing, accessing and distributing data have generated lots of benefits into the digital multimedia field. However, the visual data often contain private or confidential information or are associated with financial interests, and therefore the data security encounters a serious threat in the process of transmission due to the openness and sharing of the networks. To meet the demand of real-time secure image transmission, techniques are required to provide security functionalities like privacy, integrity, or authentication especially suited for image data types. As a matter of fact, these techniques for providing privacy and confidentiality of visual data play an important role in many applications, such as military image databases, confidential video conferences, cable TV, medical imaging system, online private photograph album, etc. To provide the protection of digital data, two complementary techniques have been developed: encryption and watermarking. Because images possess some intrinsic features, such as bulk data capacity, high correlation among adjacent pixels, redundancy of data, less sensitivity as compared to the text data, the traditional block ciphers, such as Date Encryption Standard (DES), International Date Encryption Algorithm (IDEA) and Advanced Encryption Standard (AES) are thereby not suitable for practical image encryption in real time, because their speed is low due to a bulk data volume and strong correlation among adjacent pixels [1]. Recently, chaos-based image encryption schemes [2-8] have shown their superior performance thanks to its ergodicity, pseudo-randomness and high sensitivity to initial conditions and control parameters, which are close to confusion and diffusion in cryptography. These properties make chaotic systems a potential choice for constructing cryptosystems [9, 10].

Chaos-based image cryptosystems can be classified into three categories according to their architecture, that is, permutation-only, diffusion-only and permutationdiffusion form. Among them, the permutation-only type image cipher is superior in the aspect of efficiency due to its lowest computational complexity. It only shuffles the position of each pixel in a secret order while it does not alter its gray value, therefore cannot change the histogram of plain image. The diffusion-only one changes the pixel gray value one by one or block by block, which gets greatly modified histogram for cipher-image which is generally uniform distributed and therefore significantly different from the histogram of plain image. In this sense, diffusion-only can resist the statistical analysis, differential attacks efficiently and so remedy the default of permutation-only type encryption methods. The permutation-diffusion mechanism not only permutes the pixels positions utilizing chaotic systems, but also alters the pixel gray values sequentially by some diffusion functions. The modification made to a pixel usually depends on the accumulated effect of all the previous pixels’ gray values, so that a slight change in one pixel can be spread out to almost all the subsequent pixels. However, among the existing image encryption schemes, the key streams generated by chaotic systems in both the permutation process and the diffusion process are generally fixed and independent of plain-images, which becomes the most serious flaw for chaos-based ciphers. Cryptanalysis has shown that chaos-based image encryption schemes can be broken, especially for the permutation process [11-15]. The opponents can analyze the cryptography schemes via chosen-plaintext or known-plaintext attack to obtain the key streams and so equivalently obtain the keys. The major reason lies in the keystreams yielded by chaotic systems are nothing with the plain-images. A number of chaos-based schemes with good diffusion functions are designed to resist known-plaintext attack and chosen-plaintext attack [16-19]. However there are few image encryption schemes considering the issue in the permutation process. In this paper, a novel image encryption scheme based on chaotic system with changeable parameters is proposed. An essential difference between the encryption scheme proposed here and the conventional encryption scheme is that the parameters of the chaotic system here are changing at each iteration of the chaotic system. The changeable parameters are strongly related to the plainimages and therefore the proposed permutation process can efficiently resist known-plaintext attack and chosen-plaintext attack. A diffusion function is also designed to finish the diffusion stage to make the proposed scheme more secure. In both the permutation process and the diffusion process, the key streams are generated strongly dependent on the plain-images. As a result, the proposed encryption can achieve one-time keystreams in which different plain-images will generate different keystreams. Other merits of the proposed image encryption scheme are achieved as well, including a huge key space, great sensitivity to cipher keys, good statistical properties resisting statistical attack and differential attack, good entropy analysis, etc. Experimental results have been carried out with detailed analysis to show that the proposed scheme can be a potential candidate for practical image encryption.

The rest of this paper is organized as follows. In Section II, the generalized Arnold map and the piece-wise linear chaotic map are introduced briefly. Section III proposes a novel image encryption based on chaotic system with changeable parameters dependent on plainimages. Section IV gives the detailed experiment results and security analysis. Section V makes some conclusions.

( X„ , V „ ) [0.1) 2

Therefore ⁿⁿ is confined in the unit square ^, . The map is area preserving since the determinant of its linear transformation matrix is 1. As shown in Fig.1, the unit square is first stretch by the linear transform matrix and then folded back to the unit square by the modulo operation.

The above 2D cat map (1) can be generalized to the following form by introducing two integer control parameters ^{a >0} and ^{b >0} ,

^xn +1

^yn +1

1 aa. Ifxn' [ b 1+ab Д Уп)

mod N .

The generalized Arnold map (2) h as one Ly apunov 1+ ab + a ² b ²+4 ab

C =1+------------->1

characteristic exponent                 2            , so the map is always chaotic for a>0, b > 0 .

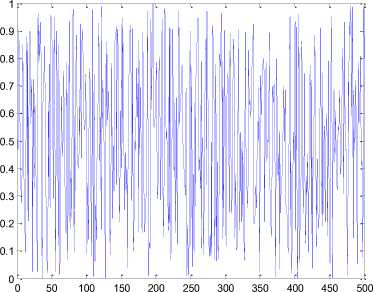
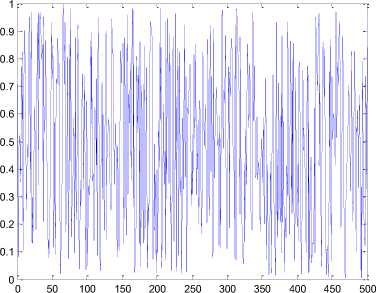
In this paper, we extend the integer control parameters ^a and ^b to real numbers. This is an essential difference from the control parameters in conventional generalized Arnold maps. As a result, we can enlarge the key space significantly. Fig. 2   (a) shows an orbit of

( x ₀, y ₀)=(0.5231,0.7412)    . , ,     , ₁ „„ , . , ,

00                  with length 1500 derived by the generalized Arnold map (2) with a=5.324, b=18.2 , the x-coordinate and the y-coordinate sequences of the orbit are plotted in Fig. 2 (b) and Fig. 2(c) respectively.

B. The piece-wise linear chaotic map

The piece-wise linear chaotic map (PWLCM) can be described as follows

xi/ p,

xi+1 = Fp(x,)=ux;-p )/(0.5-p X

Fp(1-x ),

0 < x

• II.    THE GENERALIZED ARNOLD MAP AND THE PIECE-WISE LINEAR CHAOTIC MAP

• A. The generalized Arnold map

Arnold map is also called cat map. It is a twodimensional invertible chaotic map introduced by Arnold and Avez [20]. The classical Arnold map is described by

where x _z e [0,1) , when control parameter p e (0,0.5) , the PWLCM system (3) evolves into chaotic state [21]. p and x can be served as cipher keys. The PWLCM system has uniform invariant distribution and very good ergodicity, confusion and determinacy, so it can provide excellent random sequence, which is suitable for cryptosystem.

' Xn+1 Ър . Уп+1) I1

1Yxn)2 JI Уп)

mod 1

where “ ^{x mod 1} ” means the fractional part of a real number ^x by adding or subtracting an appropriate integer.

0.8

0.6

0.5

w^

AIW 4?* A

0     0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8    0.9      1

x(k)                                                                           x(k)

(a) The orbit of (0.5231, 0.7412)

k

(b) x -coordinates sequence

k

(c) y -coordinates sequence

Figure.2. Orbit derived from the generalized Arnold map with a=5.324, b=18.2

• III.    THE PROPOSED IMAGE ENCRYPTION SCHEME

The proposed image encryption scheme consists of one permutation stage and one diffusion stage. Without loss of generality, we assume that the plain-image ^A is a gray image of size L = ^{M x} N and 256 gray-scale levels; A is an integer matrix of ^M rows and ^N columns, in which the values range from 0 to 255 representing the gray values of the digital image with 256 gray-scale levels.

• A.    Permutation stage

Given the initial conditions  x0 , y0 and control parameters a , b , we iterate generalized Arnold map (2)

. .   {( x_k , y_k ); k = 0,1,2,..., N }     . ₁

to generate an orbit    kk               0 with iteration time N0 large enough. Let

sk =floor(xk x M)+1, tk = floor(yk X N)+1.

Then ( s k , t k ), k = 0,1,-••, N ₀ must be the positions of some pixels in ^A . In case that some coordinates are the same, we delete the repeated coordinates and preserve the first one. Then the pixel values of those preserved coordinates in ^A are put in a vector ^V with length L = M x N orderly. According to the ergodicity of the Arnold map, as long as the orbit is long enough, all the coordinates of the pixels in ^A can be found in

{(floor(xk xM) +1, floor(yk xN) +1);k = 0,1,...,No}

However, one suitable ^{N 0} is applied in order to save computational time and storage, and therefore there may be some coordinates that cannot be found in the finite orbit sequence. Find out these pixel values and put in the rest part of ^V . Then reshape ^V back to one 2D matrix to

A yield the shuffled image 1 . The detailed permutation process is outlined as follows.

Step1: Set the values of x , y , a , b for the generalized Arnold map.

Step2: Iterate map (2) to generate the orbit of ( x , y ) :

{(xk,Ук): k = 0,1,2,...,No}   by the following formula fxk 1_f 1      ak-i   Ifxk-i)  ,_, 2 м

I 1=1                           I        I , k = 1,2,...,NO, кУк)  Ibk-1  1 + ak-1bk-1 JIУк-1J where a = a, b0 = b ,

ak = A (floor (xk x M) +1, floor (yk x N) +1), bk = floor(xk x M)+floor(yk x N) + 2, k = 1,2,... ND.

Throughout the paper, “ floor ” operation on x returns the largest value not greater than x .

Step3: Perform the following formula to transform ( Хк , У к ) into integer sequence:

ik = floor(xk xM) + 1,    k = 0,1,2,...N,

jk = floor(yk xN) + 1,    k = 0,1,2,...N0.

Step4: Let i be the first column and j be the second column to construct a coordinate matrix S sized N x 2 , then each row of 5 can be regarded as the coordinates of a certain pixel in A . If there are repeated coordinates in S , then only preserve the first one to get a coordinates matrix S 1 with different coordinates and size l x 2 .

Step5: Let B be a M x N indexing matrix initialized by zero matrix, then set

B(S1(i,1),51(i,2)) = 1, i = 1,2,....,l.

Find out the positions in B whose element values are zero and then place them in a vector T sized ( L - 1 ) x 2.

Step6: Permute the pixels in the plain-image to get a vector V with length L by the following way

V (i) = A(51( i ,1), 51( i ,2)),     i = 1,2,...., l,

V(l + j) = A(T(j,1),T(j,2)), j = 1,2,...,L-1.

Step7: Reshape V back to a 2D matrix to yield the shuffled image A .

• B.    Diffusion stage

Diffusion stage can enhance the resistance to statistical analysis and differential attack greatly, in which the histogram of the cipher-image is fairly uniform, and is significantly different from that of the plain-image. A slight change in one pixel could be spread out to almost all the subsequent pixels. The diffusion process is outlined as follows.

Step1: Transform the shuffled image A into a onedimensional vector denoted by q with length L = M x N .

Step2: Set the values of initial condition t and control parameter p of the PWLCM system. Iterate the PWLCM system k times to discard the transitional part and set w ( 1 ) = t .

Step3: Let ^{i =1} .

Step4: Use the following formula to yield ^{b ( i )}

b ( i ) = floor ( w ( i ) x 10¹⁴)mod256 .

Step5: Compute the pixel gray value in the cipher-image by c (i) = ((c (i -1) + q (i)) mod 256) © b (i) , where c(i) is the pixel value of cipher-image;

^{c (0)} can be set to one part of the cipher keys in the diffusion process.

Step6: Compute h by h = ^{( c (} i ) ^{mod3) + 1} to get the next w ⁽ i ⁺ 1) by iterating the PWLCM system with parameters ^p on ^{w ( i )} for ^h rounds.

Step7: Let ^{i = i +1} and return to step 4 until ⁱ arrives at ^L .

Step8: Reshape ^c back to one 2D matrix to yield the cipher-image ^{A 2} .

• IV.    EXPERIMENTAL RESULTS AND PERFORMANCE ANALYSIS

We set the initial values and control parameters as follows.

Permutation process:

x₀ = 0.3201, y₀ = 0.6317, a = 3.631, b = 27, N = 230000.

Diffusion process:

t₀ = 0.2356, p = 0.3651, c (0) = 56, k = 100.

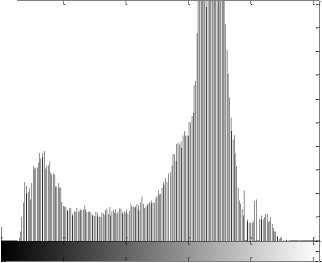
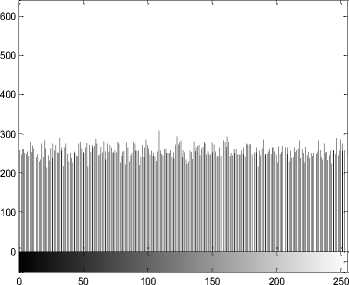
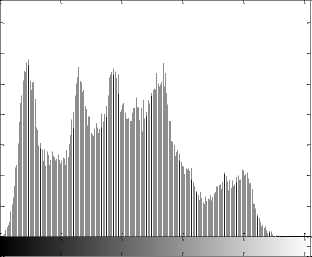
We choose the ^{256 x 256} gray images Lena and sail boat for simulation. Figs. 3(a), (c) are the plain-images Lena and sail boat respectively, Figs. 3 (b), (d) are the corresponding cipher-images respectively.

(a) plain-image Lena

(b) cipher-image of Lena

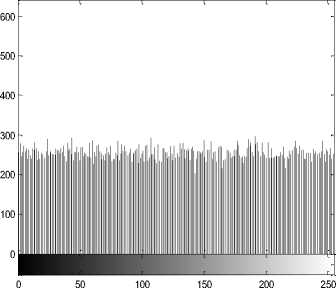
(f) Histogram of the cipher-image of Lena

(c) plain-image sail boat

100         150         200         250

(d) cipher-image of sail boat

(g) Histogram of the plain-image sail boat

(h) Histogram of the cipher-image of sail boat

Figure 3. The encrypted results.

0           50          100          150          200          250

(e) Histogram of the plain-image Lena

The crucial measure for the quality of a cryptosystem is its capability to withstand the attempts of an unauthorized participant or an opponent to gain knowledge about the unencrypted information. A good cryptosystem should resist all kinds of known attacks, such as known /chosen plaintext attack, statistical attack, differential attack, and brute-force attack. In the following subsections, security analyses have been performed for the proposed image encryption scheme, including the most important ones like key space analysis, statistical analysis, and differential attack. All the analyses show the proposed image encryption scheme is highly secure.

• A.    Key space analysis

Key space size is the total number of different keys which can be used in the encryption. A good encryption algorithm should be sensitive to the cipher keys, and the key space should be large enough to make brute-force attack impossible.

The analysis result regarding the sensitivity and the key space are summarized as follows. Assume that we want to verify the sensitivity of parameter ^K , we encrypt the plain-image ⁽^⁽, j )) M x N with K , К ^{- A K} and ^{K+ A K} respectively while keeping the other parameters unchanged, the corresponding encrypted images are A ¹ , A ² , A 3 respectively, where ^{A K} is the perturbing value. The sensitivity coefficient of parameter ^K is then calculated by

Ps (K)=-  :1  - St Ns ( A1( i, j), A (i-j))+

2 X Ml X IN i j

Ns (Ai( i, j), Аз( i, j ))]x100%

Where

Ns (x, y) = P,  x * y,

^0,  x = y.

In the case that ^{A K} is small, the larger P s ^{( K} ) means the more sensitivity for parameter ^K . Table I shows the results of the sensitivity test. The variations for the considered cipher keys are shown as follows.

Permutation process:

Aa=10-15 ,Ab=10-14, Ax0 =10-15 ,Ay =10-15,

Diffusion process:

A t0 =10-16 ,Ap=10-16 ,Ac (0)=1,Ak=1.

The result in Table I shows that the parameters x0 , y0 , a , b , t0 , p , c(0) , k are all strongly sensitive. It also implies from the result that the key space is more than10 , which is large enough to frustrate brute-force attacks.

TABLE I. SENSITIVITY OF THE CIOPHER KEYS.

K	a	b	x 0	y 0
P s ( K )	99.59	99.60	99.58	99.61
K	t 0	p 0	c (0)	k
P s ( K )	99.58	99.62	99.61	99.60

• B.    Statistical analysis

A good cryptosystem should be robust against any statistical attack. In order to verify the robustness of the proposed scheme, we perform the following statistical tests such as the histogram, information entropy, and the correlation of two adjacent pixels in the images.

• (I)    Histogram. An image histogram shows that how pixels in an image distribute by plotting the number of pixels at each gray-scale level. The histogram of the encrypted image is very important; it should not leak the information about the plain-image or the relationship between plain-image and the cipher-image. Figs. 3(e), (g) show the histograms of the plain-images Lena and sail boat respectively, Figs. 3(f), (h) are the histograms of their encrypted images respectively. From Figs. 3(f), (h), we can see that the histograms of the encrypted images yielded by the proposed encryption scheme are fairly uniform and significantly different from the histograms of the plain-images, and hence it does not provide any useful information for the opponents to perform the statistical attack.

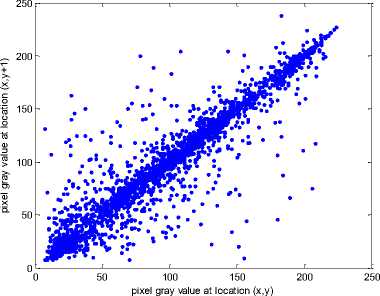
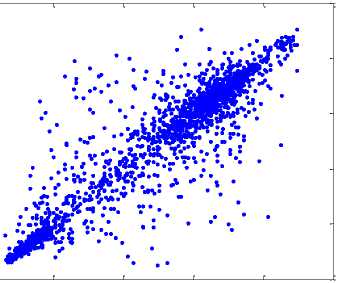
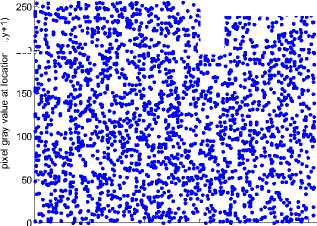
• (II)    Correlation of adjacent pixels. For an ordinary image having definite visual content, each pixel is highly correlated with his adjacent pixels either in horizontal, vertical or diagonal direction. However, an efficient image cryptosystem should produce the encrypted image with sufficient low correlation in the adjacent pixels.

To test the correlation between two adjacent pixels in plain-image and the cipher-image, we randomly select 2500 pairs of two-adjacent (at horizontal, vertical, and diagonal directions) from plain-image and cipher-image, and calculate the correlation coefficient of each pair by the following formula.

r = cov( x, y)

xy D(x) D(y) ,

cov( x, y) = £[(x - E (x ))(y - E (y))], 1T 1T

E(x) =tSx, D(x) =tS(xi-E(x)) , T i=1 T i=1

where ^x and ^y are gray-scale values of two adjacent pixels in the image, and ^T denotes the total number of samples. The correlation distributions of two horizontally adjacent pixels of the plain-image and the encrypted image produced by the proposed scheme are shown in Fig. 4, from which we can see that the strong correlation between adjacent pixels in plain-image is greatly reduced in the encrypted image. Table II shows the correlation coefficients of horizontal, vertical, and diagonal adjacent pixels for the plain-images and the cipher-images. The results indicate that the correlations of two adjacent pixels of the encrypted Lena and encrypted sail boat are much smaller compared with the plain-images, which implies that the proposed image encryption scheme is efficient to achieve good statistical nature.

TABLE II. CORRELATION COEFFICIENTS OF TWO ADJACENT IN PLAIN-IMAGES AND CIPHERIMAGES

	Horizontal	Vertical	Diagonal
Lena image	0.9439	0.9663	0.9225
Encrypted Lena	-0.0148	-0.0027	0.0015
Sail boat	0.9217	0.9242	0.8793

Encrypted sail boat     -0.0045       0.0014     0.0079

(a) plain-image Lena

л^*

^.фЖ'#"^

0         50

100       150       200       250       300

pixel gray value at location (x,y)

(b) cipher-image of Lena

pixel gray value at location (x,y)

(c) plain-image sail boat

^с;1*^о

0         50        100        150       200       250       300

pixel gray value at location (x,y)

(d) cipher-image of sail boat

Figure. 4. Correlation distributions of plain-images and cipherimages.

• (III)    Information entropy. Information entropy is the most important feature of randomness. Let ^m be the information source. The formula to calculate information entropy is

2 n - 1

H(m) = — 2 P(mi) log2 P(mi) i=0

where ⁿ is the number of bits to represent a symbol ^m i ^{G m} and ^p (m‘) represents the probability of symbol ^mi .

For a truly random source emitting ^{2 n} symbols, the entropy is H ( ^m ) = ⁿ . Therefore, for an encrypted image with 256 gray-scale levels, the entropy should be ideally H ⁽ m ) = 8 , which shows the information is completely random. Hence the information entropy of the encrypted image should be close to 8 after encryption to decrease the possibility of information leakage. The information entropy for the cipher-image of Lena is 7.9902, which implies the cipher-image is close to random sources.

• C.    Differential attack

Attackers usually make a slight change (e.g. modify only one pixel) of the plain-image and apply the proposed scheme to encrypt the original and the modified plainimages to get two cipher-images. Attackers can observe difference between the two cipher-images to find out the relationship between the plain-image and the cipherimage. This is the so-called differential attack. To test the robustness of the image cryptosystem against differential attack, two measures NPCR (net pixel change rate) and UACI (unified average changing intensity) are usually used. NPCR measures the percentage of different pixel numbers between the two encrypted images. UACI measures the average intensity of difference between the two encrypted images. They can be calculated by the following formulae:

D(i, j)

NPCR = i- j V,J ' x 100% , M x N

UACI = —¹—

M x N

c ₁( i , j )- c ₂( i , j )

¹    255

x 100%

where c and c are the two cipher-images and D ( i , j ) is defined as

J1,   c1(i, j) ^ c2(i, j),

,     [0,     otherwise.

We perform the test by changing a pixel gray value

A (23,36)

with a difference 1, for example, replace           to

A (23,36) -1

, then two plain-images are encrypted with same key to generate the cipher-images ^{c 1} and ^{c 2} . The results are shown in Tables III-IV, from which we can see that the values of NPCR and UACI can reach ^99.55% and ^33.40% at the second round. It implies that the proposed scheme is sensitivity to small changes in the plain-image, in other words, the proposed scheme can resist differential attack efficiently.

TABLE III. NPCR PERFORMANCE.

Rounds	Lena image	Sail boat
1	80.54	30.21
2	99.59	99.61
3	99.55	99.57
4	99.60	99.59
5	99.64	99.59

TABLE IV. UACI PERFORMANCE.

Rounds	Lena image	Sail boat
1	27.08	10.01
2	33.46	33.41
3	33.35	33.32
4	33.52	33.40
5	33.50	33.52

• V. CONCLUSIONS

An image encryption scheme based on chaotic systems with changeable parameters is proposed. In the proposed scheme, the parameters of the generalized Arnold map at the permutation process are changing for every iteration as they are plain-image dependent. A diffusion function is also designed to make the proposed scheme more secure. In both the permutation process and the diffusion process, the keystreams are generated strongly dependent on the plain-images. The proposed image encryption scheme can achieve one-time keystreams in the sense that different plain-images generate different keystreams. Other merits of the proposed image encryption scheme are achieved as well, including a huge key space, great sensitivity to cipher keys, good statistical properties resisting statistical attack and differential attack, good entropy analysis, etc.

ACKNOWLEDGMENT