An Image Encryption Scheme Based on Hybrid Orbit of Hyper-chaotic Systems

Published Online April 2015 in MECS

With the rapid developments of multimedia processing and network techniques in the last decades, digital multimedia data like images, videos, audios is being stored on different media, increasingly shared and communicated over the Internet and wireless networks. Protection of digital information against illegal usage becomes extremely urgent. Image encryption is a direct and efficient way to protect image information from unauthorized eavesdropping. Digital images possess some intrinsic features, such as bulk data capacity, high correlation among adjacent pixels, and human visual properties. As a consequence, traditional encryption algorithms, such as DES, RSA [1], are thereby not suitable for practical digital image encryption due to the weakness of low-level efficiency while encrypting images.

Chaotic system has been popularized in most aspects of science, such as mathematics, physics, biology, computer, finance and even arts. In particular chaotic system has been successfully introduced to modern cryptography thanks to its fantastic features, such as topological transitivity, orbit inscrutability, sensitivity to initial conditions and control parameters, pseudorandomness, etc. which meet the fundamental requirements such as mixing and diffusion in the sense of cryptography. These properties make chaotic system a potential candidate for constructing cryptosystems [2-15]. As a consequence, many chaos-based image cryptosystems have been proposed. However, most of the existing chaos-based image cryptosystems adopted low dimensional chaotic systems with permutation-diffusion architecture. The permutation–diffusion chaos-based image encryption scheme is firstly proposed by Fridrich in 1998 [2]. The proposed architecture is usually composed of two processes: chaotic confusion of pixel positions by permutation process and diffusion of pixel gray values by diffusion process, where the former permutes the plain-image pixel positions governed by a 2D chaotic map, while the latter changes the pixel gray values sequentially controlled by a 1D chaotic map, so that a tiny change for one pixel can spread out to almost all pixels in the whole image. The Fridrich architecture has become the most popular structure adopted in a great number of chaos-based image encryption algorithms subsequently proposed [2-8, 10-11]. However, some image encryption schemes based on low dimensional chaotic systems with permutation–diffusion architecture are broken recently [16-20]. The common drawbacks of permutation–diffusion based image encryption algorithms are outlined as follows. Firstly the key stream in the diffusion step only depends on the cipher key. The key streams used to encrypt different plain-images are the same if the cipher key keeps unchanged. The attacker can obtain the key stream by known-plaintext attack and chosen-plaintext attack. Secondly the two processes will become independent if the plain-image is a homogeneous one with identical pixel gray value [21]. Thirdly the cryptosystems based on low dimensional chaotic systems have some weakness, such as small key space, short periodicity and weak security. Such a kind of encryption algorithms can be generally attacked by the following steps: (i) a homogeneous image with identical pixel gray values is adopted to eliminate the confusion effect; (ii) the key-stream of the diffusion process is obtained via known-plaintext or chosen plaintext attacks; (iii) the remaining cipher-image can be regarded as the output of a kind of permutation-only cipher, which has been shown insecure and can be cryptanalyzed by known-plaintext or chosen plaintext attacks [22, 23].

It has been pointed out that the permutation process is not necessary in an image encryption scheme. Usually, omitting the permutation process will improve the executing time and make the proposed scheme more simple and easy to implement. For example, the two stages of permutation and diffusion were combined and were executing at the same time at the pixel level or bit level [7]. Regarding the security issue, hyper-chaotic systems can be employed to improve the security of the cryptosystem proposed [7, 24]. Higher dimensional chaotic systems with higher dimensional attractors shall have good chaotic features. The adopting of higher dimensional chaotic systems which own more than one positive Lyapunov exponents clearly improves the security of encryption scheme by generating more complex dynamical behavior or high randomness. It is more difficult to predict the chaotic sequences generated by higher dimensional chaotic systems. Therefore, some high dimensional chaotic systems are used in image encryption.

In this paper, we propose an image encryption scheme based on hybrid orbit of hyper-chaotic system and diffusion-only mechanism. As far as we know, image encryption scheme based on hybrid orbit of hyper-chaotic system only with diffusion operation has not been reported. The adopting of hybrid orbit of hyper-chaotic system can enlarge the key space efficiently and therefore enhance the security. Given two sets of initial states, the fourth order Ronge-Kutta method is used to generate two orbits of the hyper-chaotic system consisting of four ordinary differential equations. Tent map is applied to generate one pseudo-random sequence to determine the hybrid orbit points from which of the two yielded orbits. Based on the improved hyper-chaotic sequences derived by the hybrid orbit, we design an image encryption scheme with plain-image dependent key stream. The proposed scheme applies different key streams when encrypting different plain-images (even with the same hybrid hyper-chaotic sequences). To make the proposed scheme resist differential analysis attack, we perform one diffusion process with two rounds of diffusion operation which depends on both the cipher keys and the plainimage. The diffusion process can modify the pixel values and break the correlations between adjacent pixels of an image simultaneously. The security and performance analysis of the proposed image encryption are carried out using the histograms, correlation coefficients, information entropy, key sensitivity analysis, differential analysis, key space analysis, etc. All the experimental results show that the proposed image encryption scheme is highly secure and excellent performance, which makes it suitable for practical application.

The rest of the paper is organized as follows. In Section II, we briefly introduce the hyper-chaotic system and discuss its chaotic natures. The improved hybrid sequence from hyper-chaotic sequences is outlined as well. Section III devotes to designing the image encryption scheme. One diffusion function is presented to encrypt images. In Section IV, we present the results of security and performance analysis of the proposed image encryption scheme using the histograms, correlation coefficients, information entropy, key sensitivity analysis, differential analysis, key space analysis, encryption rate analysis, etc. Section V concludes the paper.

• II.    The Hyper-Chaotic System and Its Hybrid Orbits

• A.    The hyper-chaotic system

  The notation of hyper-chaotic system is firstly put forward by Rössler in 1979 [25]. Hyper-chaotic system is a high order ordinary differential equation, which is widely applied in cryptography and circuit design. Hyper-chaotic system presents more than one positive Lyapunov exponents and therefore generates more complex dynamical behavior or high randomness. The hyper-chaotic sequences generated surely improve the security of encryption scheme. In this paper, a hyper-chaotic system is used in key scheming and modeled by

x = a ( y - x ) + yz , у = cx - y - xz + w, Z = xy - bz , . w = dw - xz ,

where a , b , c and d are system parameters. When a = 35, b = 8/3, c = 55, d = 1.3 , the Lyapunov exponents of system (1) are ^ = 1.4164 , ^ = 0.5318 , ^ = 0, ^ =- 39.1015, implying that system (1) exhibits a hyper-chaotic behavior. For the initial condition ( x , y , z , w ) , one can obtain four hyper-chaotic sequences { x , y , z , w : i = 1, 2, 3,---} by the fourth order Runge–Kutta algorithm. These hyper-chaotic sequences are non-periodicity and very sensitive dependence on initial conditions ( x , y , z , w ) . Setting the initial conditions ( x₀ = 5, y₀ = 10, z₀ = 5, w₀ = 10) and integration step h=0.001, we solve system (1) and get the first 5000 real values of each sequence. The corresponding sequence pairs are depicted in Figure 1.

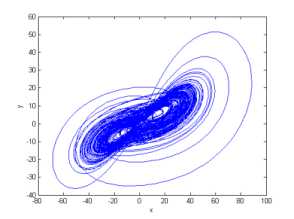
(a) x - y projection

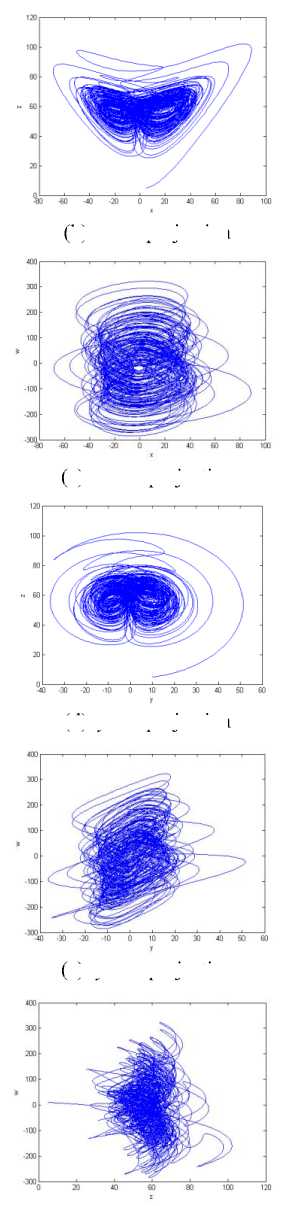
(b) x - z projection

(c) x - w projection

(d) y - z projection

(e) y - w projection

(f) z - w projection

Fig.1. The phase diagrams of hyper-chaotic sequence pairs.

• B.    Generation of hyper-chaotic sequences

Assume that we need one hyper-chaotic sequence with length L . Set the initial condition to be ( x ¹ , y ¹ , z ¹ , w ¹ ) one can solve system (1) by the fourth order Runge–Kutta algorithm to obtain four hyper-chaotic sequences

{ x , y , z , w : i = 1, 2, 3<--, L /4} . Then we process the four hyper-chaotic sequences to be four 8-bit gray value sequences by

s * = mod(| fix ( s_t - fix ( s_t )) x 10¹⁴ |, 256)         (2)

where fi ( x x ) rounds the elements of x to the nearest integers towards zero, mod( x , y ) represents the remainder of x divided by y . We then get four hyper-chaotic sequences { xs 1 , ys \ , zs\, ws ^ , i = 1,..., L /4} . We integrate the four sequences to be one mixed sequence 5 ¹ = { k 1 , i = 1,..., L } by

1     11      11     1

^k 4 i - 3 = xs i , ^k 4 i - 2 = ys i , ^k 4 i - 1 = zs i , k = ws ¹, i = 1,2,..., L /4.

Set the initial condition to be ( x ², y ², z ², w ²) different from ( x ¹ , y ¹ , z ¹ , w ¹ ) ， one can similarly obtain another integrated sequence S ² = { k ², i = 1,..., L }.

• C.    Generation of hybrid hyper-chaotic sequences

The tent map is used to generate one random sequence {^,n = 1,...,L} which is quantized to be one two-value sequence {ln,n = 1,...,L} . ln is used to determine kln to form one hybrid sequence {kln, n = 1,2, • • •, L} . The chaotic tent map is defined by ti+1

I q ’ ⁰

1 - t i

1- q ^,

: ti <  q

, t e [ 0,1 ] , i = 1,2, _ , n ,      ⁽⁴⁾

q <  t <  ¹

where q is the control parameter, t is the state variable, t is the initial value. The tent map shows good chaotic nature, including ergodicity, pseudo-randomness, high sensitivity to control parameters and initial values, etc. Set the control parameter and initial value q = 0.3, t0 = 0.4, we iterate the system (4) to get chaotic sequence {tn,n = 1,...,L} , and yield the choice sequence by l = floor(t, x2) +1,i = 1,2,_,L .        (5)

To improve the computation efficiency, we introduce two counter variables T (1), T (2) , which are used to count the number of points selected from the k th hyper-chaotic sequence S^k . T (1), T (2) are initialized to be zero. As the k th hyper-chaotic sequence S^k is chosen, T ( k ) is increased by 1. When the hybrid hyper-chaotic sequence with length L is finally generated, 5 2^ _T ( i ) = l . We denote i =1

the hybrid hyper-chaotic sequence with length L to be {mk, i = 1,..., L} yielded by mkf = k1*^ ,i i = 1,2,..., L.                  (6)

• III.    The proposed image encryption scheme

We assume that the plain-image is a 8-bit gray-scale image of size L = M x N , it is an integer matrix of M rows and N columns, in which the values range from 0 to 255. The 2D pixel gray value matrix can be convert to a 1D vector P = { p_x , p ₂,..., p_L } , where p . denotes the gray level of the image pixel in the row floor ( i / N ) and column mod ( i , N ) , where floor ( x ) rounds x to the nearest integer less than or equal to x . The hyper-chaotic system (1) is used to generate the initial chaotic key stream. The image encryption scheme is based on the final secret key stream which is not only related on the original chaotic key stream but also the plain-image. The image encryption scheme includes generating initial chaotic key stream and two rounds of diffusion operation.

• A.    The generation of initial chaotic key stream

Step 1. Input the initial conditions ( x ¹ , y ¹ , z ¹ , w ¹ ) and ( x 2 , y 2 , z 2 , w 2 ), set the step h , and integer N _o >  500 , the control parameter and initial condition q , t , integer C e [ 0,255 ] .

Step 2. Solve the hyper-chaotic system (1) with the initial conditions   ( x ¹, y ¹, z ¹, w ¹) and  ( x ², y ², z ², w ²)

respectively. Discard the first N _o -1 points of the orbits to overcome the transient effect. Set the N th points ( x ¹ _{N 0}, y ¹ _{N 0}, z ¹ _{N 0}, w ¹ _{N 0}) and ( x_N ²₀, y_N ²₀, z_N ²₀, w_N ²₀) to the new initial conditions.

Step 3. Iterate the tent map (4) for N _o + L times, and discard the first N transient points and preserve the remainder which is still denoted as {t , i = 1,..., L } , and then generate the two-value orbit choice sequence Ln = (1 1 ,l 2 ,..., I l ).

Step 4. To reduce the workload, we count the number of 1 and 2 in Ln = (l_x , l ₂,..., l_L ). It is then easy to calculate needed orbit point numbers T and T of the two hyper-chaotic orbit derived from the new initial conditions ( x ¹ _{N 0}, y ¹ _{N 0}, z ¹ _{N 0}, w ¹ _{N 0}) and ( x_N ²₀, y_N ²₀, z_N ²₀, w_N ²₀) . We note that T_x and T ₂ should satisfy 4 x ( T + T ₂) >  L and can be calculated by

T = ceil ( sum(Ln == j ) /4) , j = 1,2, where sum(x == y )  denotes the total number of

x(i) = У (i), i = 1,2, * * *, L ,   ceil(x) rounds x to the nearest integer greater than or equal to x .

Step 5. Solve the system (1) by initial condition ( x ¹ , y ¹ , z ¹ , w ¹ ) and step h and get four hyper-chaotic sequences{ x ^ , y 1 , z 1 , w ¹, i = N _o + 1,..., N _o + T (1)}. We then generate the first improved hyper-chaotic sequence { k 1 , i = 1,...,4 T } by (2) and (3). Similarly the second improved hyper-chaotic sequence { k 2 , i = 1,..., 4 T ,} is either generated with initial condition ( x ² , y ² , z ² , w ² ) and step h .

Step 6. Combine the improved hyper-chaotic sequences { k 1 , i = 1,...,4 T } and { k 1 , i = 1,...,4 T ₂} to be one hybrid initial key stream { mk .} , i = 1,..., L by (6).

• B.    Two rounds of diffusion operation

Assume that the 2D gray value matrix of the plainimage is converted to be one vector P = { p_x , p ₂,..., p_L } , and C = { c , c ₂,..., c_L } denotes the corresponding vector of the cipher-image. One diffusion process is outlined as follows.

Step 1. Set i = 1.

Step 2. Compute the first pixel gray value of the cipher-image by using the first pixel gray value of the plain-image, the integer C and the first initial key stream element mk by cx = bitxor(px, bitxor(mod(C0 + mkx, 256), mkx)) , where bitxor (x, y) returns the result after bitwise XOR operation.

Step 3. Let i = i + 1, and calculate the next pixel gray value of the cipher-image by using c , the i th pixel gray value of the plain-image and the i th initial key stream element mk by

• c. = bitxor ( p_t , bitxor (mod( c ._ j + mk _z., 256), mk ._ j ))

Step 4. Return to Step 3 until i = L , and finally we get the cipher-image vector C = { c , c ₂,..., c_L } after one round of diffusion.

Step 5. Set i = 1.

Step 6. Utilized the first pixel gray value c , the last one c , and mk to get c by cx = bitxor (cx, bitxor (mod( cL + mkx, 256), mkx))

Step 7. Let i = i + 1, then calculate c_t by

• c. = bitxor ( c ., bitxor (mod( c ._ _t + mk ., 256), mk^ _t))

Step 8. Return to Step 7 until i = L . The finally yielded vector C = { c , c ₂,..., c_L } is the resulted cipherimage after two rounds of diffusion operation.

• IV.    Security and performance analysis

According to the basic principle of cryptology [1], an ideal encryption cryptosystem requires sensitivity to cipher keys, i.e., the cipher-text should have close correlation with the keys. Furthermore, an ideal encryption scheme should have a large key space to make brute-force attack infeasible; it should also well resist various kinds of attacks like statistical attack, differential attack, etc. Some security analysis will be performed on the proposed image encryption scheme, including the most important ones like key sensitivity test, key space analysis, statistical analysis, and differential attack analysis. The plain-image is 256 gray-scale and of size 256 х 256 (including Lena, Boat, Cameraman). In the simulation experiment, we set two initial conditions

(x0 = 5, y0 = 10, z0 = 5, w0 = 10) , (x0 = 10, y02 = 5, z 02 = 10, w2 = 5), and step h = 0.001 , No = 1000 , Co = 3 , q = 0.3 , t0 = 0.4. All the analysis shows that the proposed image encryption scheme is highly secure thanks to its high sensitivity of the control parameters and initial conditions of the considered chaotic systems, large key space, and satisfactory diffusion mechanism.

• A.    Key space analysis

  Key space consists of all the possible cipher keys. A good image encryption scheme needs to contain sufficiently large key space for compensating the degradation dynamics in PC. It should be also large enough to effectively resist brute-force attack and prevent invaders decrypting original data even after they invest large amounts of time and resources. We can just set the two initial conditions ( x 1 , y 1 , z 1 , w 1 ) , ( x 2 , y 2 , z 2 , w 2 ) of the hyper-chaotic system, the initial condition t and the control parameter q of chaotic tent map to be the cipher keys. If they are represented as floating number with precision 10^-14 , then the number of x ¹ is 10¹⁴ , Therefore the total cipher keys will be as many as (10¹⁴)¹⁰ ® 0⁴⁶⁵ , which is large enough to make brute-force attack infeasible.

• B.    Statistical analysis

Shannon pointed out in his masterpiece [26] the possibility to solve many kinds of ciphers by statistical analysis. Therefore, passing the statistical analysis on cipher-image is of crucial importance for a cryptosystem. Indeed, an ideal cryptosystem should be robust against any statistical attack. In order to prove the security of the proposed encryption scheme, the following statistical tests are performed.

• (i)    Histogram analysis. We encrypt the plain-image Lena (Figure 2(a)) and get the cipher-image Figure 2(b). We also plot the histograms of plain-image and cipher-

• image as shown in Figures 2(c)-(d). Figure 2(d) shows that the histograms of cipher-image is fairly uniform and significantly different from the histogram of the original plain-image Figure 2(c). Hence it does not provide any useful information for the opponents to perform any statistical analysis attack on the encrypted image.

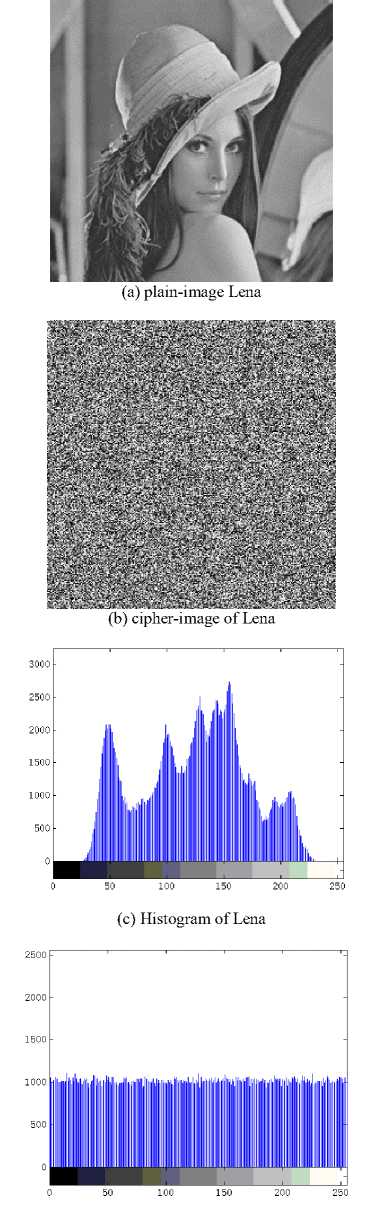
(d) histogram of cihoer-image of Lena Fig. 2. The histogram analysis result.

• (ii)    Correlation analysis of adjacent pixels. To test the correlation between two adjacent pixels, the following performances are carried out. First, we select 1000 pairs of two adjacent pixels randomly from coefficient of the selected pairs using the following formulae:

Cr =   cov ⁽ x , y ) ,

VD(x ) D(y ) ’ 1T cov(x.y) = ~Z(X -E(x))(y-E(y)).

T i =1

TT

E ( x )=^ xi, D ( x )=7^( xi - E(x)) , where x, yare the gray-scale values of two adjacent pixels in the image and T is the total pairs of pixels randomly selected from the image. The correlations of two adjacent pixels in the plain-image and in the cipherimage are shown in Table 1. It is clear from Table 1 that the proposed image encryption technique significantly reduces the correlation between the adjacent pixels of the plain-image.

Table 1. Correlation between adjacent pixels of plain-image and cipher-image.

	horizontal	vertical	diagonal
Plain-image Lena	0.9446	0.9718	0.9206
Cipher-image of Lena	0.0003	0.0005	-0.0060
Plain-image Boat	0.9233	0.9409	0.8815
Cipher-image of Boat	0.0145	-0.0124	-0.0118
Plain-image Cameraman	0.9415	0.9626	0.9167
Cipher-image of Cameraman	0.0762	0.0163	-0.0494

(iii) Correlation between plain-images and cipherimages. We have also analyzed the correlation between plain-image and cipher-image by computing the two-dimensional correlation coefficients between of plain-image and cipher-image. The 2D-correlation coefficients are calculated by

c

AB

H x W

HW

ZZ ( A-. j - A )( B- j - B ) i = 1 j = 1

H X W

HW

ZZ ( Aj- A ) 2

i = 1 j = 1

H X W

HW

ZZ ( B i ,- B ) 2

i = 1 j = 1

where A represents one of the red green and blue channel of the plain image B represents one o f the re d green and blue channel of the cipher image A and B are the mean values of the elements of 2D matrices A and B respectively; M and N are respectively the height and width of the plain/cipher image. We have computed the correlation coefficients for the pair of plain-image Lena and its corresponding cipher-image. The results are shown in Table 2. One can see from the results that the correlation coefficients between plain-image and cipherimage are very small (or practically zero) hence the cipher-image owns the characteristics of a random image.

HW         HW a=---EEA. B=---EEB.

H X W ^{Z Z} i . j      H X W ^{Z Z} i . j

Table 2. Correlation between plain-image and cipher image.

Image	Encryption CC	entropy	PSNR	Decryption CC
Lena	-0.003545	7.9972	9.3566	1.0
Boat	-0.002246	7.9970	9.3530	1.0
Cameraman	0.000475	7.9971	8.3771	1.0

H ( m ) = - Z -1 p ( m i )log( p ( m i )) (bits) . i =0

where L is the total number of symbols m p ( m ) represents the probability of occurrence of symbol m and log denotes the base 2 logarithm so that the entropy is expressed in bits. For a random source emitting 256 symbols. its entropy is H ( m ) = 8 bits. For a 8-bit gray image, the information entropy is given as

28-1                        1

H ( m ) = Z P ( A )log2— (bits).

• i =0                P ⁽ I i )

  We have calculated the information entropies for plainimages and their corresponding cipher-images. The results are shown in Table 2. The value of information entropy for the cipher-image produced by the proposed image encryption scheme is very-very close to the expected value of truly random image, i.e., 8bits. Hence the proposed encryption scheme is extremely robust against entropy attacks.

  (v) Peak signal-to-noise ratio analysis. Another parameter to describe the encryption quality is the peak signal-to-noise ratio (PSNR). This term is described based on that the mean squared error (MSE) is calculated. This criterion provides the error between input image and output image. The MSE value is

  
  

  D ( i , j )

  NPCR =    ,       x 100% ,

  M x N

  
  

  UACI = —¹—

  M x N

  
  

  c ₁( i , j )- c ₂( i , j )

  ^T    255

  
  

  x 100%

  
  

  where c and c are the two cipher-images and D ( i , j ) is defined by

  
  

  D ( i , j ) =

  
  

  1, 0,

  
  

  c 1 (i , ^j ) * c 2 ⁽ i , ^j ), otherwise.

  
  

  f I

  mse = ----У УГ Mi , A - Mi , j Л,

  I M x N t tL O (  ) E (

  
  

  where I_o ( i , j ) is the pixel value of plain-image, I_E ( i , j ) is the pixel value of cipher-image. Thus the PSNR is described by

  
  

  PSNR = 20log

  
  

  I max

  MSE

  
  

  where I is the maximum of pixel value of the image. The PSNR should be a low value, which corresponds to great difference between the original image and the encrypted image. To determine the encryption quality, the PSNR is computed for the encryption of Lena, Boat and Cameraman. In Table 2, the PSNR values are shown in the fourth column. The results show that these PSNR values are all very low. Therefore, the encryption quality is good in sense of PSNR.

  C. Sensitivity Analysis

  To test the sensitivity of cipher keys and plain-image, two measures NPCR (net pixel change rate) and UACI (unified average changing intensity) are usually used. NPCR measures the percentage of different pixel numbers between the two encrypted images. UACI measures the average intensity of difference between the two encrypted images. They can be calculated by the following formulae:

  
  

  The NPCR for two random images, which is an expected estimate for an ideal image cryptosystem, is given by NPCR_&pected = (1 - 2 - L ) x 100%, where L is the number of bits used to represent all the gray values of the considered image. f or a 8-bit gray scale image L , hence NPCR Expected = 99.6094%.

  The UACI for two random images, which is an expected estimate for an ideal image cryptosystem, is

  1    T ² L ^{- 1} i ( i + ¹)

  given by UACI Expected = -2 L -----^x100%. For a 82      2 — 1

  bit gray image, UA^CI Expected = 33.⁴⁶³5% .

  (i) Key sensitivity analysis. A good image encryption scheme should be extremely sensitive to cipher keys, which is an essential feature for any good cryptosystem in the sense that it can effectively prevent invaders decrypting original data even after they invest large amounts of time and resources. Assume that we want to verify the sensitivity of cipher key K , we encrypt the plain-image A = ( A ( i , j ))_MxN with K and K + A K respectively while keeping the other keys unchanged, the corresponding encrypted images are A , A respectively, where AK is the perturbing value. We then calculate the corresponding NPCR,UACI,CC and PSNR. We set the perturbing value to be 10 ^{— 10} and get the results shown in Table 3. All the experimental results show that the cipher keys are all strongly sensitive.

  
  

  	Table 3. Key sensitivity analysis
  Perturbing value	NPCR       UACI         CC         PSNR
  A x = 10 — 10 A y = 10 — 10 A z = 10 — 10 A w = 10 — 10 Aa = 10 — 10 A tn = 10 — 10	99.6338         33.6484          -0.0071           7.7203 99.5880         33.3717           0.0047          7.7648 99.6017         33.3773           0.0057          7.7687 99.6124         33.3265           0.0084          7.7757 99.5956         33.4732           0.0013           7.7355 99.6124         33.4483           0.0047          7.7498

  
  
99.5942 -----------1-----------1-----------1-----------1-----------1-----------1-----------1-----------1-----------1----------- 99.594 -- 99.5938 -- 99.5936 -- 99.5934 -- 99.593 -- 99.5928 -- 99.5926  --- 11= 99.5924 -- 99.5922 -----------¹-----------¹-----------¹-----------¹-----------¹-----------¹-----------¹-----------¹-----------¹-----------

(ii) Plain-image sensitivity analysis. The differential cryptanalysis of a block cipher is the study of how differences in a plaintext can affect the resultant differences in the ciphertext with the same cipher key. It is usually done by implementing the chosen plaintext attack but now there are extensions which use known plaintext as well as ciphertext attacks also. As for image cryptosystems, attackers may generally make a slight change (e.g., modify only one pixel) of the plain-image, and compare the two cipher-images (obtained by applying the same cipher key on two plain-images having one pixel difference only) to find out some meaningful relationships between the plain-image and the cipherimage. If a meaningful relationship between plain-image and cipher-image can be found in such analysis, which may further facilitate the opponents to determine the cipher key. If one minor change in the plain-image will cause significant, random and unpredictable changes in the cipher-image, then the encryption scheme will resist differential attack efficiently. To test the robustness of image cryptosystems against the differential cryptanalysis, We have performed the differential analysis by calculating NPCR and UACI on plain-image Lena. The analysis has been done by randomly choosing 100 pixels (one at a time, including the very first and very last pixels) in each plain-image and changing their all three color values by one unit. The average values of NPCR and UACI thus obtained for all three images are given in Figure 3. It is clear that the NPCR and UACI values are very close to the expected values, thus the proposed image encryption technique shows extreme sensitivity on the plaintext and hence not vulnerable to the differential attacks. The average of the 100 NPCR values is 99.5926% and the average of UACI is 33.4136%, they are both highly close to their expectation values 99.6094% and 33.4635% respectively.

£ 99.5932 -                                                        I-

0    10    20    30    40    50    60    70    80    90100

• (a) 100 NPCR values

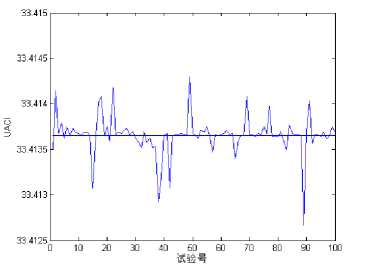
(b) 100 UACI values

Fig. 3. The differential analysis.

• D.  Resistance to known-plaintext and chosen-plaintext

attacks

It follows from the encryption scheme that mk is related to the initial cipher keys of the hyper-chaotic system, and c depends on the pixel gray values of the plain-image. Hence, the pixel gray values of the plainimage are employed to change the final encryption keys except for the first pixel in the first round of diffusion operation. Hence, the final encryption keys depend on not only the initial state value of the hyper-chaotic system, but also the plain-image. When different plain-images are encrypted, the corresponding key stream is not the same. The attacker cannot obtain useful information by encrypting some special images since the resultant information is related to those chosen-images. Therefore, the attacks proposed in Refs. [16–20] become ineffective on this new scheme. The proposed scheme can well resist the known-plaintext and the chosen-plaintext attacks.

• V. Conclusions

In this paper, a novel plain-image dependent encryption scheme based on hybrid orbit of hyper-chaotic system is proposed. Two hyper-chaotic sequences are generate from one hyper-chaotic system and then are improved and integrated into one hybrid sequence to achieve better randomness and security for image encryption. One diffusion procedure with two rounds of diffusion operations are performed, which makes the key stream depend on both the initial hybrid hyper-chaotic sequence and plain-image. Therefore, the key stream in the encryption process depends on both the initial keys and the plain-image and the cipher-image can resist the known-plaintext and chosen-plaintext attacks efficiently. The key space is large enough to resist brute-force attacks as well. All the performance analysis shows that the scheme can well prevent the image from statistical attacking and that the scheme possesses high key sensitivity and gets a good ability to resist differential attack. With high-level security, it can be used in internet applications, such as network security and secure image communications.