An Image Hiding Scheme Using 3D Sawtooth Map and Discrete Wavelet Transform

Published Online July 2012 in MECS DOI: 10.5815/ijigsp.2012.06.08

Thanks to the rapid developments of multimedia and network technology, various data in digital form is transmitted over the Internet network. The transmitted data can be a digital representation of text, image, audio and video. They can be replicated, edited easily and spread openly through the Internet, which causes a serious problem that it is difficult even impossible to give proof of copyright once pirated. The security issue of digital images has attracted more attentions consequently. In order to ensure the security of the data transmission over the Internet, data encryption [1] and data hiding [2] are two widely used approaches. Data encryption is a technique to protect data from illicit access by transforming important data into meaningless code. Nevertheless, data hiding is different from data encryption as it conceals the existence of secret data by hiding the secret data into a meaningful host data to distract the attention of the observers.

A variety of image encryption algorithms (for example, see [3-14] and the references therein) have been studied and developed in the last two decades. Among them, chaos-based encryption algorithms have been considered to be a significant and potential technique in application thanks to chaotic systems’ good properties in many concerned aspects such as security, complexity, speed and computational overhead, etc. As a matter of fact, due to some intrinsic features of digital images, such as bulk data capacity and high correlation among adjacent pixels, traditional encryption algorithms such as DES, IDEA and RSA [15] are not suitable for practical digital image encryption. The fundamental features of chaotic systems, such as ergodicity, pseudo-randomness and high sensitivity to initial conditions and control parameters, are close to confusion and diffusion in the cryptography.

Digital image hiding methods are ways of hiding secret images in host images such that an unintended observer will not be aware of the existence of the hidden images. Host images embedded the secret images are called stego-images. For digital image hiding methods, the image quality refers to the quality of the stego-images. The image hiding technology may be implemented in the frequency domain or in the spatial domain of a given digital image. One of the most common techniques in the spatial domain is based on manipulating the least-significant-bit (LSB) planes by directly replacing the LSBs of the host image with the secret message bits [16]. The LSB substitution scheme is irreversible, as a result, the host image can not be recovered exactly from the stego-image after extracting the hidden secret image. In the frequency domain, the host images and/or the secret images are transformed by DCT, DWT, etc. and then the proposed image hiding schemes are employed to the transformed images. For example, Ahmidi proposed a color image technique based on DCT, embedding the image into middle frequency coefficients of transformed blocks [17]. Hsieh proposed a watermarking method based on the qualified significant wavelet tree (QSWT) [18], where the embedding scheme took the relationships of DWT coefficients and spatial information into consideration. Many applications can benefit from image hiding schemes, including confidential video conferencing, pay-TV, confidential facsimile, medical applications.

In this paper, we apply the image encryption technique and the image hiding technique together to enhance the security, and improve the robustness against malicious attacks. An image hiding scheme with the preprocessing of secret image by the proposed encryption scheme is presented. Two 3D sawtooth maps with three control parameters are utilized to encrypt the secret image which will be imbedded in one host image. The encryption scheme consists of generating a chaotic orbit by one 3D sawtooth map to scramble the pixel positions and yielding a random gray value sequence by another sawtooth map to change the gray values. The encrypted secret image and the host image are transformed by DWT and then are merged in the frequency domain. The recovered secret images also show that the proposed image hiding scheme is robust against various attacks.

The rest of this paper is organized as follows. Section II introduces the 3D sawtooth map. One image encryption scheme is proposed in Section III. The image hiding scheme is presented and the robustness tests are performed in Section IV. Section V concludes the paper.

• II.    3D sawtooth map

The sawtooth map So : [0,1] ^ [0,1] is given by x I a,        if x g [0, a),

S ₀( x ) = 1           ,

[ ( x — a ) I (1 - a ) ,    if x g [ a , 1] ,

where x g [0,1] is the state of the system, and a g (0,1) is the control parameter. It is a noninvertible transformation of the unit interval onto itself. As a = 0.5 , map (1) becomes the well-known regular Bernoulli shift map Bo : [0,1] ^ [0,1] given by xn+1 = B0(xn ) := 2xn mod1

= A

² x n ,

I ² x n — 1 ,

if xn g [0,112) if xn g [1I2,1]

The Bernoulli shift map (2) yields a simple example for an essentially nonlinear stretch-and-cut mechanism, as it typically generates deterministic chaos. Such basic mechanisms are also encountered in more realistic dynamical systems. The sawtooth map is continuous and piecewise linear, with the linear regions [0 , a ] and [ a , 1] . Note that the slope of the left branch is 1 I a >  1 and the slope of the right branch is 1 I (1 — a ) >  1 . For any a g (0 , 1) , the piecewise linear map (1) has Lyapunov exponent — a ln a — (1 — a ) ln(1 — a ) , which is larger than 0, implying that the map is chaotic.

In this paper, we extend the sawtooth map to its 3D version S : [0 , 1] 3 ^ [0 , 1]³ by the following way.

1      (x,., z), abc (x, y, z) g [0, a) x [0, b) x [0, c), (x, y, z—c), (x, y, z) g [0, a) x [0, b) x [ c, 1], a b 1 — c (3) (x,     b, z), (x, y, z) g [0, a) x [ b, 1] x [0, c), a 1 — b c (x,     b, z), (x, y, z) g [0, a) x [ b, 1] x [ c, 1], S (x, y, z) = . a 1 — b 1 — c (,y, z), (x, y, z) g [ a, 1] x [0, b) x [0, c), 1 — a b c (,y, z), (x, y, z) g [ a, 1] x [0, b) x [ c, 1], 1 — a b 1 — c x — a y — b z (7      , 7      , _), (x, y, z) g [ a, 1] x [ b, 1] x [0, c), 1 — a 1 — b c x — a y — b z — c. ;1—a 1—b 1—c), (x, y, z) g [ a, 1] x [ b, 1] x [ c, 1]. where a, b, c g (0,1) are the control parameters. It is easy to show that the three Lyapunov exponents are (see [19])

A = a ln(—) + (1 — a) ln(—1—), a1

A = b ln(1) + (1 — b )ln(-L), b1

A = c ln(1)+(1 — c )ln(-L)). c1

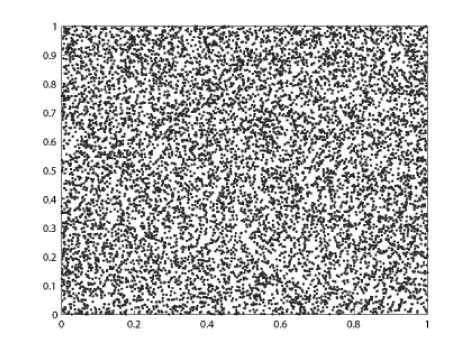
It is obvious that ^ , A , A are all positive, implying that the 3D sawtooth map is chaotic on [0 , 1]³ . A typical orbit of ( x ₀, y ₀, z ₀ ) derived from the dynamical system is {( x_k , y_k , z_k ) = T ( x o , y о , z 0 ) , k = 0 , 1 ,-••}, which is shown in Fig. 1 for x ₀ = 0 . 21 , y₀ = 0 . 83 , z ₀ = 0 . 46 , a = 0 . 5 , b = 0 . 3 , c = 0 . 7 The plotting orbit points fill [0 , 1]³ as long as the orbit is long enough, which indicates that the system is chaotic visually. The control parameters a , b , c and the initial condition x ₀, y₀ , z₀ can be regarded as cipher keys as the map is used to design image encryption schemes.

(a)

(b)

(c)

Figure 1. Orbit derived from the considered 3D sawtooth map with x^ = 0 . 21 , y^ = 0 . 83 , z^ = 0 . 46, a = 0 . 5 , b = 0 . 3 , c = 0 . 7 . (a), (b), (c) are the xy , xz , yz -projections of the derived orbit respectively.

• III.   The Proposed Image Ecryption Scheme

• A.    Image encryption scheme

We propose an image encryption scheme consisting of two processes: diffusion of pixel gray values and permutation of pixel positions. In the permutation process, the 3D sawtooth map is utilized to realize the shuffling of pixel positions. In the diffusion process, another sawtooth map is utilized to generate a pseudo-random gray value sequence, then bitxor operation and mod operation are performed to change the pixel gray values so that the histogram of the cipher-image is significantly different from that of the plain-image, therefore enhancing the resistance to statistical attack and differential attack greatly. The opponent can not find any useful clues between the plain-image and the cipher-image and so can not break the cryptosystem even after they have spent a lot of time and effort. Let the plain-image to be P with height H and width W . The image encryption scheme is outlined as follows.

Step 1. Set the initial values and the control parameters

xx = 0.367, yx = 0.761, zx = 0.579,ax = 0.413, b = 0.684, c = 0.725

Step 2. Iterate the 3D sawtooth map to get three sequences { x_i } , { y_i } , { z_i } ,

(X+1, y+1, zi+1) = S(xi, y, zA i = I'" HW -1  (4)

Step 3. Sort the sequence { x : i = 1,---, HW } to get index vector I_x , i = 1 , 2 ,..., HW . Rearrange the gray value matrix P to be a vector with size 1 x HW . We still name the vector P .

Step 4. Permute the pixel positions by

P1( i) = P (Ix ), i = 1,2,..., HW

to get the scrambled image P 1 .

Step 5. Set i = 1 ,

P2(1) = P1(1) Ф [floor(L x (yx + z) / 2) mod L]  , where floor(x)denotes the largest integer number not larger than x , L is the gray-scale level.

Step 6. Set

c(i) = floor (L x y.), d (i) = floor(L x z.).

Perform the diffusion by the bitxor operation by

P 2( i +1) = P 2( i) Ф [(floor ((c (i) + d (i)) / 2)

+ P1(i + 1))mod L ].

Step 7. Set i = i + 1 and repeat Step 6 till i = HW - 1 .

We note that the above diffusion process implies that it can not influence the pixels before the tampered pixel with a gray value change. As a remedy, we here add a reverse diffusion process as a supplement to the above diffusion process.

Step 8. Set the initial values x * = 0 . 347, y * = 0 . 532, z * = 0 . 864 and the control parameters a ₂ = 0 . 346 , b = 0 . 539, c ₂ = 0 . 912 . Set j = 1 and calculate

u (M x N) = floor(L x x*),

v (M x N) = floor (L x y *),

w(M x N) = floor(L x z*),

P3(M x N) = P2(M x N) Ф [ floor((u(M x N)

+ v (M x N) + w( M x N)) / 3) mod L ].

Step 9. calculate

u (j) = floor(L x xj ),

V(j) = floor(L x yj ),

w (j) = floor (L x Zj), where x1 = x *, yx = y *, zx = z *.

Let

5 = 1 + [ P 3( M X N - j + 1)mod2] , and iterate the 3D sawtooth map s times to get

⁽ x j + 1 , y_{J +} i , z j + 1 ) :

(xj+1, yj+1, zj+1) = ^ (xj, yj, zj ).                    (7)

The reverse diffusion is

P 3( M X N - j ) = P 3( M X N - j + 1) ®

[⁽ floor ⁽⁽ и ⁽ j ) + v ⁽ j ) + w ⁽ j )) / ^{3)    (8)}

+ P 2( M x N - j ))mod L ].

Step 10. Set j = j + 1 and repeat Step 9 till

j = M x N -1.

The obtained matrix P 3 is reshaped to be a matrix Q with height H and width W , Q is the cipher-image. The plain-image Lena is encrypted and the result is shown in Fig. 2(b).

(a)

(b)

Figure 2. The encryption results. (a) plain-image, (b) cipher-image

• B.    Security analysis

According to the basic principle of cryptology [15], a good encryption scheme requires sensitivity to cipher keys, i.e., the cipher-text should have close correlation with the keys. An ideal encryption scheme should have a large key space to make brute-force attack infeasible; it should also well resist various kinds of attacks like statistical attack, differential attack, etc. In this subsection, key sensitivity analysis and statistical analysis are performed. All the analysis shows that the proposed image encryption scheme is highly secure.

Shannon pointed out in his masterpiece [20] the possibility to solve many kinds of ciphers by statistical analysis. Therefore, passing the statistical analysis on cipher-image is of crucial importance for a cryptosystem. Indeed, an ideal cryptosystem should be highly robust against any statistical attack. In order to prove the security of the proposed encryption scheme, the following statistical tests are performed.

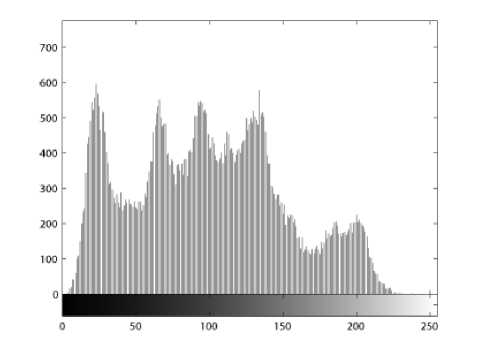
• (i)    Histogram. Encrypt the image Lena with one round, and then plot the histograms of plain-image and cipherimage as shown in Fig. 3. Fig. 3(b) shows that the histogram of the cipher-image is fairly uniform and significantly different from the histogram of the original image and hence it does not provide any useful information for the opponents to perform any effective statistical analysis attack on the encrypted image.

• (ii)    Correlation of adjacent pixels. To test the correlation between two adjacent pixels, the following performances are carried out. First, we select 1000 pairs of two adjacent pixels randomly from an image and then calculate the correlation coefficient of the selected pairs using the following formulae:

cov ( x , y )

Cr = DEx)5 V Dy ),

T

cov(x, y) = T ^ (x - E(x))(y, - E(y)), i=1

TT

E(x) = T X x--’ D(x) = T X(xi- E(x))2, i =1                            i =1

where X , y are the gray-scale values of two adjacent pixels in the image and T is the total pairs of pixels randomly selected from the image. The correlations of two adjacent pixels in the plain-image and in the cipherimage are shown in the Table I .

(a)

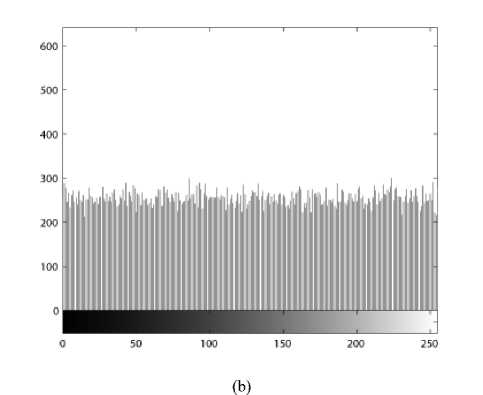
Figure 3. (a) Histogram of plain-image, (d) Histogram of cipher-image

Table I. Correlation coefficients of two adjacent pixels in two images.

	Plain-image	Cipher-image
Horizontal	0.9387	-0.0244
Vertical	0.9682	-0.0128
Diagonal	0.9112	-0.0231

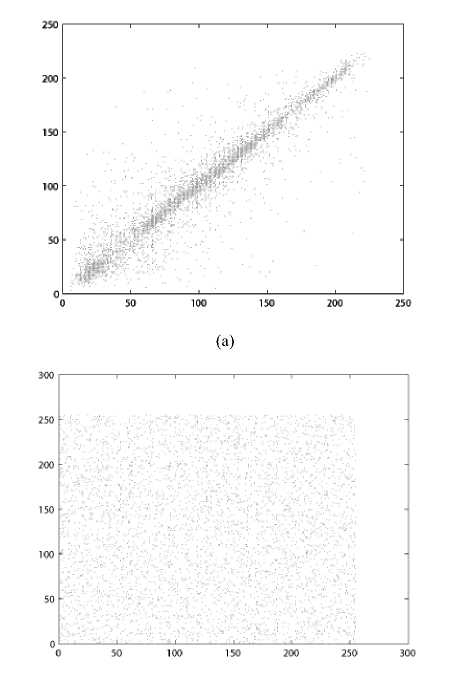
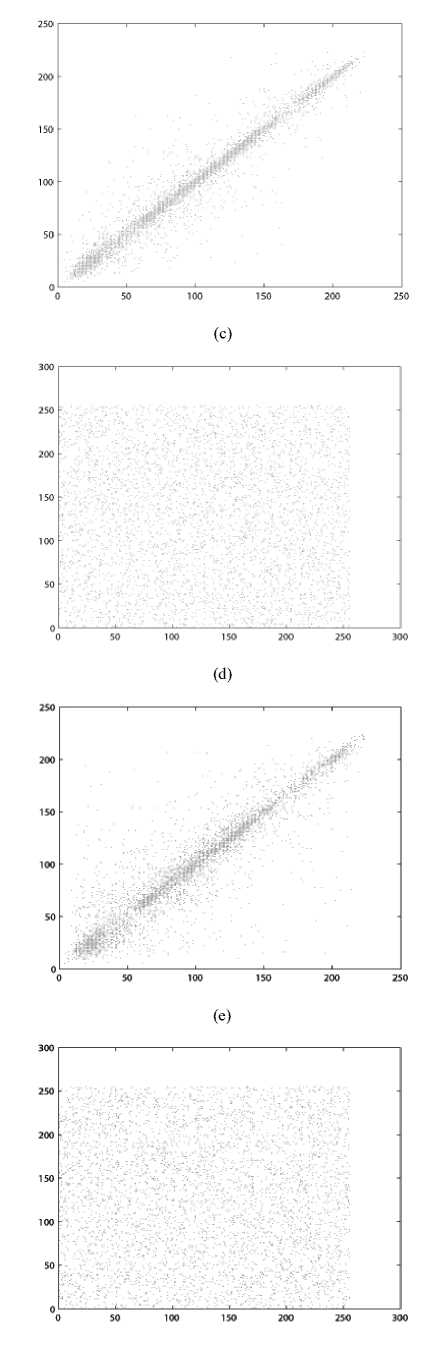
The correlation distribution of two horizontally adjacent pixels in the plain-image and that in the cipherimage are shown in Fig. 4.

(b)

(f)

Figure 4. Correlations of two adjacent pixels in the plain-image and in the cipher-image: (a), (c), (e) are for the plain-image; (b), (d), (f) are for the cipher-image.

A good image encryption scheme also needs to contain sufficiently large key space for compensating the degradation dynamics in PC. It should be sensitive to cipher keys as well, and thus can effectively prevent invaders decrypting original data even after they invest large amounts of time and resources. The analysis results regarding the sensitivity and the key space are summarized as follows. Since the permutation process is irrelevant to the diffusion process, the key space consists of the cipher keys in both processes. Therefore, the control parameters a_x , b , c_x ( i = 1 , 2) and the initial condition x_o , y₀ , z ₀, x *, y *, z * constitute the cipher keys. The sensitive tests with respect to all cipher keys have been carried out. To verify the sensitivity of key parameter K , the original plain-image I = ( I ( i , j))_HxW is encrypted with K = p , K = p — A S and K = p + A S respectively while keeping the other key parameters unchanged. The corresponding encrypted images are denoted by | , I^ , I₃ respectively. The sensitivity coefficient to the parameter K is denoted by the following formula:

P (K) = ,  2  ,V £ [ Ns (11 (i- j), 12 (i- j»

2 x H x W j

+ Ns (Ii(i, j), Iз( i, j))] x100%% where

^N s ⁽ x ^- У )

= <

1 ,

x * У, x = У,

and A S is the perturbing value. P ( K ) implies the sensitivity to the perturbation of parameter K . The greater of P ( K ) , the more sensitive for the parameter K . Table 1 shows the results of the sensitivity test where the initial key values are set to be the following

x = 0.367, y = 0.761, zx = 0.579,

a = 0.4, b = 0.6, cx = 0.7,

x* = 0.347, y* = 0.532, z* = 0.864, a2 = 0.3, b2 = 0.5, c2 = 0.9

The variations A S of the considered parameters are all set to be 10 ¹⁶ .

We apply the proposed image encryption scheme one round with only perturbing one cipher key K with the corresponding variation value while fixing other parameters.

Table II. Results regarding the sensitivity to cipher keys.

K	x 1	y 1	z 1	a 1	b 1	c 1
P s ( K )	0.9963	0.9961	0.9962	0.9961	0.9959	0.9962
K	x *	y *	z *	a	b 2	c 2
P s ( K )	0.9964	0.9957	0.9963	0.9961	0.9962	0.9960

• IV.    Image hiding Scheme

An image hiding scheme is proposed in this section. We first use the encryption scheme proposed in Section III to encrypt the secret image; the encrypted secret image and the host image are transformed by DWT and then are merged in the frequency domain. The secret image can be detected or extracted easily. The image hiding scheme is proposed as follows:

Step 1. Apply the encryption scheme to encrypt the secret image P sized H x W , we get a cipher secret image P .

Step 2. Transform the host image J with size H x W and the encrypted secret image P by DWT with two-level SYM4 wavelet and get the corresponding coefficient matrices J and Q , which are merged by the following formula:

R = ^Qi + (1 — a)J1, t e (0,1).

Step 3. Transform the merged matrix R by the inverse wavelet transform to get the stego-image H .

We note that the merging factor a e (0,1) should be chosen suitably in the imbedding scheme. If a is too large, the quality of the host image will be influenced. If a is too small, the information of the secret image becomes weak and it is difficult to extract the secret image. The extraction scheme is just the inverse of the imbedding scheme. Fig. 3 shows the hiding results where the 256X256 secret image Lena is imbedded in the host image Cameraman sized 256X256 with a =0.17. The experimental results are shown in Fig. 5.

(a)

(b)

(a)

(c)

(b)

(d)

Figure 5. The hiding results: (a) secret image Lena, (b) host image cameraman, (c) stego-image, (d) extracted secret image.

(c)

Experiments are performed to test the robustness of the proposed image hiding scheme. Attacks in the experiments are cropping, salt and pepper noising, JPEG compression. Experimental results show the proposed scheme is robust against the considered attacks. All the attacking tests are applied to the stego-image with the same parameters as those in Fig. 5. The experimental results are shown in Fig. 6.

(d)

(e)

(f)

Figure 6. Results of attacking tests: (a) cropping attack with cut-off 128X128; (b) the extracted secret image from (a); (c) salt & pepper noising attack with density 0.02; (d) the extracted secret image from (c);

(e) JPEG compression attack with quality 70; (f) the extracted secret image from (e).

• V.   Conclusions

In this paper, the 3D sawtooth map is utilized to generate chaotic sequences for permuting the pixel positions and changing the pixel values to achieve the encryption of the secret images which are embedded in the host images. Simulation shows that the encryption scheme is secure and the image hiding scheme is robust against various kinds of attacks.

Acknowledgment

This research was supported by National Natural Science Foundation of China (No. 11071152) and Natural Science Foundation of Guangdong Province (No. 10151503101000023).