An Improved Convexity Based Segmentation Algorithm for Heavily Camouflaged Images

Published Online March 2013 in MECS

Intelligent image processing systems are becoming increasingly important and have been applied in various fields like biomechanics [1], [2], education [3], [4], [5], [6], medical [7], [8], [9], photography [10], biometrics [11], [12], [13], [14], [15], [16], [17] motion tracking [18], [19], [20], [21], [22], [23], [24], defense [25], surveillance [26], character recognition [27], [28], [29], bioinformatics [30], [31], etc.

“Camouflage is an attempt to obscure the signature of a target and also to match its background” [1].Work related to camouflage can be roughly divided into two sections: camouflage assessment and design [2] and camouflage breaking. Despite the ongoing research, only little has been said in the computer vision literature on visual camouflage breaking [3], [4], [5], [6].

The paper presents evidence that gray level convexity can be effectively used for segmenting heavy camouflaged images. This is based on Thayer’s principle of counter-shading [7], which observes that some animals use apathetic coloration to prevent their image (under sun light) from appearing as convex graylevels to a viewer. This indicates that other animals might perform camouflage breaking activity depending on the convexity of graylevels they see (or else there was no need in such an apathetic coloration). We inspired from this approach aim at detection of heavily camouflaged objects using 3D concavity and convexity. The purpose of the operator is detection of convex or concave objects in highly cluttered scenes, and in particular under camouflage conditions.

In order to perform this task, we directly apply the suggested operator D on the intensity function. D responds to smooth 3D concave and convex domains based on 3D structure of objects. The operator is robust as it is neither limited to any particular light source nor on the reflectance function.  The robustness and invariance characterizing D   [7] as well as the biological motivation make it suitable for camouflage breaking, even for camouflages that might delude a human viewer. As compared to the present attempts for camouflage breaking, this operator is independent of conditions. The target should be 3D convex of concave was the only previous assumption.

D operator is able to segment the camouflaged object effectively from the background in majority of images. In certain cases, the operator also extracts additions sub targets with the object of interest due to the significant three dimensional responses of the sub targets. The problem is solved with an improved algorithm proposed in this paper. The algorithm combines the ability of convexity based algorithm with thresholding. The improved algorithm was able to segment targeted object effectively and overcome the inability of the conventional convexity algorithm. The proposed method is compared with the conventional ^{D arg} operator. It is also compared with some conventional edge based operator for performance evaluation.

We define the convexity based operator D in the next section. Intuition for D is given in section 2.1 which also gives particular importance for understanding its behavior. Camouflage breaking using Dlrg is given in section 3. The evidence for camouflage breaking by grey level convexity is given in section 3.1. The advanced method is proposed in section 4. The edge operators are presented in section 5 while the experimentation results are elaborated in section 6. Finally, section 7 gives the concluding remarks.

• II.    OPERATOR FOR CONVEXITY DETECTION

This section the operator used for detecting the 3D objects with smooth convex and concave domains. Assuming I ( x , y ) as the input image, its gradient map in Cartesian representation is

VI (x, y) = (- (I (x, y)), - (I (x, y))). dyd

Let us convert V I ( x , y ) into its polar representation. We can define gradient argument by:

(,9d

0(x, y) = ag VI(x, y)) = arctan I (—(I(x, y)), —(I(x, y))) ^ dy where the two dimensional arc tangent function is:

y arctan( )

x arctan( y, x) = <

arctan( y )   + n

x

arctan( y) - n x and the one dimension arctan(r) denotes the inverse function of tan(r) so that: arctan(r): [-да, +да] ^ [- П,+П]. The idea behind the computation of the convexity of the object, which is denoted as Y is simple y-derivative of argument map:

^Yarg =l" ^e(x , у ) = "l" ^arctan | ⁽ l" ⁽ I ⁽ x , у )), l" ⁽ I ⁽ x , у ))) |     (13)

8y        S y      ( 8y        8x        )

We obtain isotropic operator by applying Y operator on each image rotating it each time by 0, 90, 180, 270 and rotating them back to the original positions. The result of operator D is the sum of the four responses. arg

A. Intuition for Y

Intuition for Y is divided into three sections as arg described below.

• 1.    What does Y detect?

• 2.    Why detect zero crossings of gradient argument?

• 3.    Intuition summary

arg

Zero-crossings of the gradient argument is detected by the function Y . This stems from the last step of the gradient argument calculation: the two-dimensional arctangent function. In the negative part of x-axis, the arctangent function is discontinuous which cause its y- derivative approach infinity. It implies that when Y cross the zero axis, it approaches infinite when moving towards the negative x-axis of the arctan function. Zero crossings of the gradient argument is known by infinite limit.

Zero crossings of the gradient argument applied on the intensity function I ( x , y ) is detected using the function Y . The existence of zero crossings of the gradient argument enforces a certain range of values on the gradient argument (values which are typical near x = 0; y < 0). Assuming that I ( x , y ) as a surface in ЗД ³ , then the normal to its surface represents the direction of gradient argument. A range of values of gradient argument implies the certain range of directions which are normal to the intensity surface. This enforces on the intensity surface itself. The structure of intensity surface as either a paraboloidal structure or any strongly monotonically increasing transformation which can be derivable of a paraboloidal structure is characterized in [8]. The local approximation of 3D convex and concave surfaces can be done by paraboloids since they are arbitrarily curved surfaces. (Recall, that our input is discrete, and the continuous functions are only an approximation!). The domains of detected intensity surfaces are exhibited by 3D concave and convex structure. The convexity is three dimensional, because this is the convexity of the intensity surface I(x; y) (= 2D surface in R3;), and not convexity of contours (= 1D surface in R2. This 3D convexity of the intensity surface is characteristic of intensity surfaces emanating from smooth 3D convex bodies.

With the infinite response of Y at negative x-axis (of arctan), zero-crossings of gradient argument is detected. When the intensity surface is 3D convex or concave, zero crossings of arctangent occur. 3D convex intensity surfaces are generally produced by convex smooth 3D objects. Therefore, by detecting the infinite responses in Y lead to detection of intensity surface domains which characterize 3D smooth concave and convex subjects.

Fig. 1. Thayer's principle of countershading is explained using ray tracing when applied to cylinder

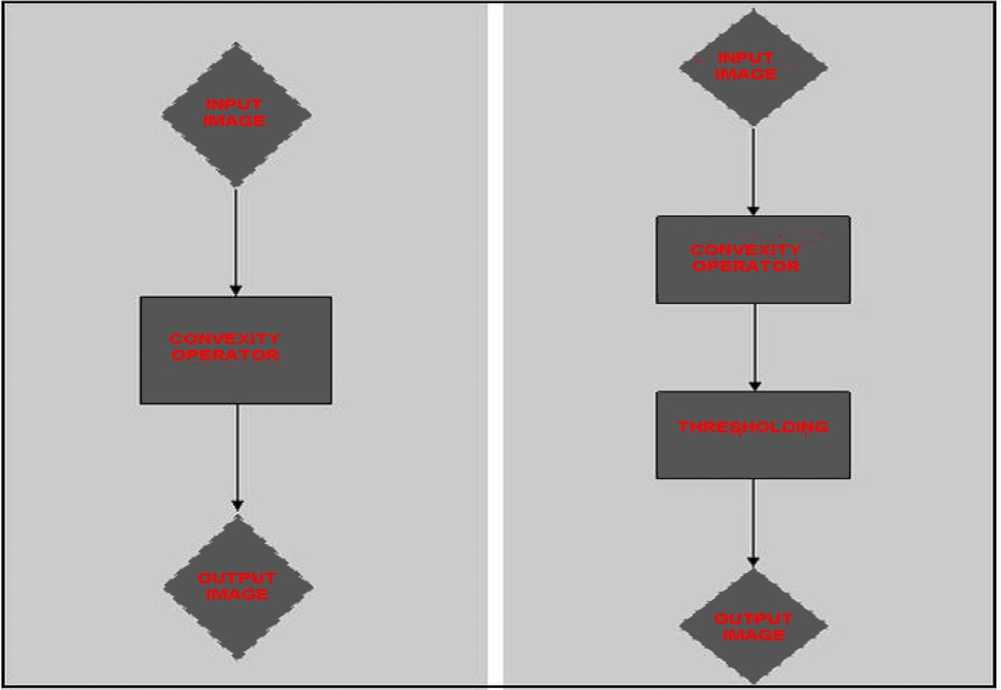
Fig. 2. (a) Flow of chart of standard convexity operator (b) Flow of chart of advanced proposed convexity operator

• III.    CAMOUFLAGE BREAKING

Through study on robustness of operator under various conditions like illumination, scale, orientation, texture was performed in [7]. As a result, the smoothness condition of the detected 3D convex objects can be relaxed. In this paper, robustness demands are further increased by introducing very strong camouflage and further comparing the efficiency of the method with some standard edge operators.

• A. Biological motivation

We now exhibit the biological evidence of camouflage breaking using convexity of the intensity function. This matches our idea of camouflage breaking by convexity detection (using D ). By further evidence, we can show that not only can intensity convexity break camouflage, but also there are animals whose coloring is suited to prevent this specific technique of camouflage breaking. We very well know that a smooth 3D convex object produces a convex intensity function under directional light. Explaining this in biological aspect is that when an animal trunk (subject) is exposed to lighting of sun, the observer can see the shades which are convex intensity function. Thus, these shades can probably reveal the animal, especially in surroundings which break up shadows (e. g. woods) [7]. The biological evidence given above encourages us to useD modus operand for camouflage breaking which detects the convexity of intensity function. During thousands of years of evolution, the ability to trace an animal based on these shadow effects which can be dissolved by the coloration of animals. The effect of counter shading coloration was observed first during the earlier century which can be known from Thayer’s principle. Portmann [7] describes Thayer’s principle: “If we paint a cylinder or sphere in graded tints of gray, the darkest part facing toward the source light, and the lightest away from it, the body’s own shade so balances this color scheme that the outlines becomes dissolved. Such graded tints are typical of vertebrates and of many other animals”. Thayer's principle of countershading is explained using ray tracing when applied to cylinder’s is shown in figure 1. When the animal is under top lighting (sun light), the gradual change of albedo neutralizes the convexity of the intensity function. If no countershading has been used, the intensity function would have been convex, exposing the animal to convexity based detectors (such as D ). By the effect of countershading, convexity of intensity function neutralizes, thus disabling convexity based detection. The existence of counter-measures to convexity based detectors implies that there might exist predators who use convexity based detectors similar to D . The flow chart of the arg convexity operator is shown in fig. 2 (a).

• IV.    PROPOSED METHOD

The proposed method is a combination of the convexity operator and thresholding resulting into an advanced method capable of spotting the target of interest while eliminating the sub-targets. Once the convexity operator is applied on the image, the operator identifies the object of interest due to its three dimensional property and acknowledges the features points on the object. In addition, the operator also identifies the features points on other sub-targets due to their three dimensionality. In order to eliminate the response on the sub-targets thresholding is applied resulting into only the desired targets. The flow chart of the proposed method is shown in fig. 2 (b).

• V.    STANDARD SEGMENTATION ALGORITHMS

A number of effective algorithms have been used in the past for edge detection. The basic aim of any edge detection algorithm is to locate the points in an image where its pixel intensity changes sharply. In general, edges in any image define the corresponding object and hence are helpful in identification of objects in a image or video sequence. Some of the edge detection algorithms are briefly discussed below:

• A.    Canny edge detector

The operator uses an initially noise removal methodology on the image under scrutiny followed by edge detection. The different steps involved in this method are:

• •    Noise Reduction : The raw image is convolved with a Gaussian filter which results in a slightly blurred version of the original which is not affected by noise to any significant degree.

• •    Finding the intensity gradient of the image : In the blurred image, horizontal, vertical and diagonal edges are detected by using the algorithm. The edge detection operator returns a value for the first derivative in both horizontal and vertical directions from which the gradient and its direction can be determined.

I ^P l = V ( P x У + ( P ) 2                         (1)

To the gradient magnitude non-maximal suppression is applied. By this, we get a set of edge points in the form of a binary image.

• •    Double Thresholding : In this method only a certain edge pixels of the image which have not been covered till the end of step 3 are marked. The edge pixels above the high threshold are marked as strong and the ones below the low threshold are suppressed. The edge pixels between the two are marked as weak.

• •    Edge Tracking by hysteresis: Strong edges are included in the final image and weak edges are

included only if they are linked to strong edges. Obviously noise won’t result in a strong edge and hence strong edges are considered to be true edges. Weak edges can either be due to true edges or noise variations. The weak edges due to true edges are more likely to be linked to strong edges.

• B.    Sobel Operator

It is a differentiation operator which roughly computes the gradient of the function that symbolizes the intensity of an image. The Sobel operator performs a 2-D spatial gradient measurement on an image and underlines regions of high spatial frequency symbolizing the edges. The operator comprises of a pair of 3x3

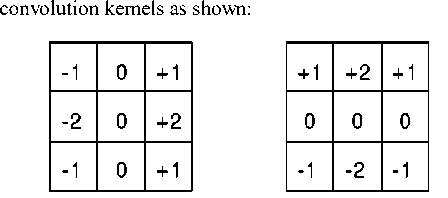
P xy

Fig 3. Kernals that are convoluted with source image for sobel operator

These kernals are convolved with the source image to find the derivatives in both horizontal and vertical directions. The absolute magnitude of the gradient at each point of the image is given by:

I PI = ^ Px )2 +(P )2

The gradient can be approximated as

I PI=1 P+1 P                                  (3)

The direction of the gradient is given by

. ( P y ) a = arctan — ()

V Px )

The convolution kernals of the Sobel edge detector are larger due to which the input image is smoothed to a larger extent, thus making it less sensitive to noise.

• C.    Roberts Edge Detector

The Robert Cross operator performs a 2-D spatial gradient measurement on a source image. It gives us the regions of high spatial frequency corresponding to edges. This operator consists of a pair of 2x2 convolution kernals as shown:

+1	0
0	-1

0	+1
-1	0

response. The Prewitt edge detector otherwise doesn't differ much from the Sobel operator.

Px

Py

Fig. 4. Kernals that are convoluted with source image for Roberts Edge Detector

The source image is convolved with these two kernals resulting in both horizontal and vertical gradients. The absolute magnitude of gradient at a point is given by:

I PI = ^ Px )2 +(Py )2

The gradient can be approximated as:

IP = IP + 1 Py\

E. Laplacian of Gaussian

This edge detector involves a combination of Gaussian filtering and the Laplacian operator. In this method of edge detection initially the noise in an image is decreased by convoluting that particular image with a Gaussian filter. By this all the noisy points are filtered out or removed from the image. After this step a gradient measurement is done on the image and the edges of the image are identified. This is done by detecting the zero-crossings of the second order difference of the image. The mechanism of working of the laplacian of Gaussian is as follows: The image is first smoothed by convolution with a Gaussian kernel of width ° to filter out all the noise present in the image. The Gaussian kernel in its standard terms is given by

The direction of the gradient is given by:

Г - ( x ² + y ² )

G ° ( x , У ) = -j— e ^L ' 2 2°°

a = arctan — l Px

The laplacian of the image whose intensity values are represented as f ( x , y ) is defined as

The advantage of the Roberts edge detector is that it works quite fast because of its small size. However it is irresistant to noise and also fails in detecting very sharp edges.

L ( x , y ) = —- + —- 9 x ²    d y ²

D. Prewitt Edge Detector

This edge detector calculates the maximum response for a set of convolution kernels and finds the orientation of edges of each pixel of the image under consideration. In most of the edge detection techniques finding the magnitude of orientation of the edges in x and y directions is tedious. The Prewitt edge detector overcomes this problem by finding the orientation straightforward from the kernel with the maximum

Since the input image is shown as having discrete pixels, we need to approximate the second derivatives in the equation for laplacian operator. As the convolution operation is associative, the Gaussian filter can be convolved with the laplacian filter and then the hybrid filter can be convolved with the image to get the results. The 2-D LoG function is given by:

LoG (x, y) = —1 1-n°

2°2

_ x ² + y ² e 2 °°

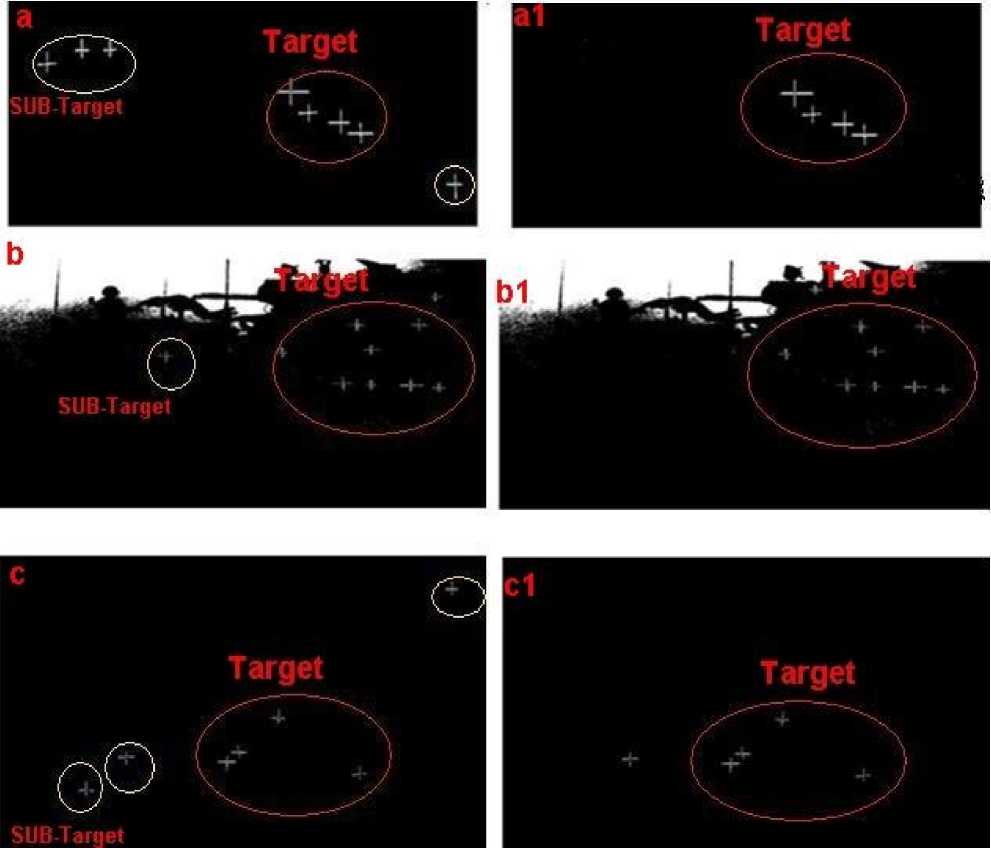
Fig. 8. Comparison of standard convexity operator with the advanced operator (a) Output of standard operator applied on first input image showing target and sub-targets (a1) Output of proposed operator applied on first input image showing target (b) Output of standard operator applied on second input image showing target and sub-targets (b1) Output of proposed operator applied on second input image showing target (c) Output of standard operator applied on third input image showing target and sub-targets (c1) Output of proposed operator applied on third input image showing target

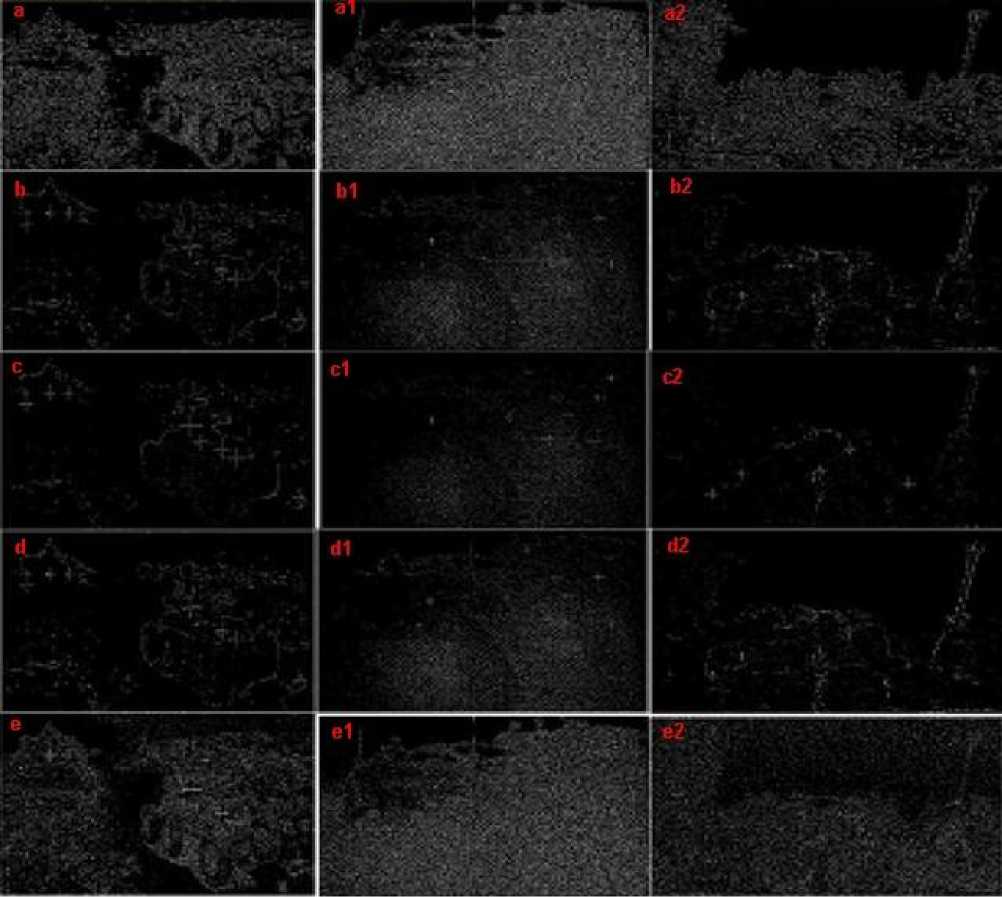
Fig. 9. The output of Sobel applied on the input images is shown in Fig. (a), (a1), (a2) respectively, the output of Canny applied on the input images is shown in Fig. (b), (b1), (b2) respectively, The output of Roberts applied on the input images is shown in Fig. (c), (c1), (c2) respectively, the output of laplacian of Gaussian applied on the input images is shown in Fig. (d), (d1), (d2) respectively, the output of Prewitts applied on the input images is shown in Fig. (e), (e1), (e2) respectively

• VI.    EXPERIMENTAL RESULTS

The section explains and elaborates the results obtained for the simulations performed upon the highly camouflaged military images. The section compares the results of the proposed algorithm with the results obtained by applying the standard convexity operator and standard edge operators on the dataset. The experiments were performed on MATLAB 7.10.0.499 version on 2.2GHz processor.

The standard convexity operator is first applied on the images dataset of military camouflage tanks as shown in fig. 5. The target of interest and the sub-targets can be seen in the figure. The operator identifies the tanks in the input image due to the three dimensional response as shown in fig. 6 (a). The operator is applied on additional two images to prove the effectives on the method as shown in Fig. 6 (b) and Fig. 6 (c).

In addition to the identification of target of interest, the operator also spotted undesired sub-targets in the image which also displaced three dimensional responses. In order to eliminate the undesired response, we used the advanced method proposed in the paper. The result for the advanced method, after application on the input images is shown in fig. 7. It is evident that thresholding eliminates the response from the sub-targets leaving only the targets of interest. Similar results are obtained for application on other two images as shown in fig. 7 (b) and fig. 7 (c).

Further, a comparison is performed between the results obtained from the conventional operator with the proposed operator as shown in fig. 8. It is clearly evident that the sub-target is eliminated due to thresholding introduced in the advanced method. Similar results are obtained for application on other two images as shown in fig. 8 (b) and fig. 8 (c).

The efficiency of the proposed method is also proved across five standard edge operators namely Sobel, Canny, Roberts, laplacian of Gaussian and Prewitts. The edge operator work on grayscale variation using the edges to identify the object. It is observed that the edges in the image are weak leading to poor results as shown in fig. 9. The output of Sobel applied on the input images is shown in Fig. 9 (a), (a1), (a2) respectively, the output of Canny applied on the input images is shown in Fig. 9 (b), (b1), (b2) respectively, The output of Roberts applied on the input images is shown in Fig. 9 (c), (c1), (c2) respectively, the output of laplacian of Gaussian applied on the input images is shown in Fig. 9 (d), (d1), (d2) respectively, the output of Prewitts applied on the input images is shown in Fig. 9 (e), (e1), (e2) respectively On the other hand, the

D advanced arg operator uses the intensity of the three dimensionality of the object for identification leading to efficient results.

• VII.    CONCLUSION

In order to eliminate the unwanted targets thresholding is combined to get the desired targets, which resulted into highly efficient results. The effectiveness of advanced convexity operator is demonstrated by multiple experiments performed in the paper. Finally, the superiority of the proposed method is proved over the standard convexity camouflage breaker ( D ) and edge-based operators namely Canny edge arg detector, Sobel operator, Roberts edge detector, Prewitt edge detector and Laplacian of Gaussian. Convexitybased camouflage breaking was found very robust and in all the cases much more effective.