An Improved Method of Geometric Hashing Pattern Recognition

Published Online June 2011 in MECS

Object recognition is the key task of many vision systems. Object recognition methods are often used in many applications. For example, robot pick up of a tool on an assembly line ， database image queries, structural molecule comparison, fingerprint and face recognition, detection of irregularities on medical images, etc.

This study is supported by the NSFC project (No.70572050) and the Project for Science and Technology Development of Zhengzhou (No.10PTGG399-2)

Especially object recognition is widely used in the industrial products assembly and inspection tasks, where often an image of an object must be aligned with a model of the object. The pose obtained by the object recognition process can be used for quality control.

Humans recognize a multitude of objects in images with little effort, despite the fact that the image of the objects may vary somewhat in different view points, in many different sizes/scale or even when they are translated or rotated. Objects can even be recognized when they are partially obstructed from view. This task is still a challenge for computer vision based systems in general.

Several methods have been proposed to recognize objects in images by matching 2D models to images [1]. The simplest classical recognition method is based on gray value of the model and image itself and uses normalized cross correlation or the sum of squared absolute differences as a similarity measure [1]. Normalized cross correlation is invariant to linear brightness changes but is very sensitive to clutter and occlusion as well as nonlinear contrast changes. A more complex object recognition method uses object edge for matching [2]-[3]. Ballard (1981 [2]) generalizes the Hough transform (Hough, 1962) to detect arbitrary shapes. Ballard takes the edge orientation into account, which makes the algorithm faster and also greatly improves its accuracy by reducing the number of false positives, the weakness of the generalized Hough transform algorithm is to be provided with huge parameter space (x, y,θ, s) . It requires large amounts of memory to store the accumulator array.

Excellency of geometric hashing has been demonstrated in many applications [3]-[6].Common substructures can be found in a scene regardless of rotation, translation, scale, and occlusion using geometric hashing. Geometric hashing method is quite powerful in recognition precision. However, the complexities of modeling and recognition phases are the third power of the pattern feature points and scene feature points, respectively. When there are a large number of feature points in the pattern and the scene, the recognition process will be time consuming. Thus it is necessary to develop a fast object recognition technique.

In this paper, we describe some modification of Geometric hashing pattern recognition scheme to improve its recognition speed. Firstly, the edge of object image is extracted as feature points, and the pattern is decomposed into a series of sub-patterns. Second the sub-patterns are record in a plurality of hash tables. Finally we speed up the modeling and recognition phases by combining image pyramid with edge direction information. Both complexity analysis and experiment evaluations demonstrate the efficiency of this technique.

• II.    OVERVIEW OF GEOMETRIC HASHING

Geometric hashing is a general model-based pattern matching technique, which is robust to partial occlusion as well as clutter. The geometric hashing paradigm consists of two stages. The first stage is an off-line model preprocessing step, in which the object recognized is represented by a group of feature points and model data is compiled into a hash table for fast access in the recognition stage. The hash table is accessed via invariants derived from scene features. Conventionally, these invariants are obtained by defining a coordinate frame based on a k-tuple subset of the features, such that all other features can be expressed in this frame in a manner which is invariant to all possible transformations that the feature set may undergo during the imaging process.

A disadvantage of the using of point features in conventional geometric hashing is that their extraction, especially in the presence of image noise, is particularly prone to errors. It has been shown that the standard geometric hashing technique is consequently rather sensitive to noise. To improve the recognition performance of conventional geometric hashing, we can consider improving the extraction of feature point, the selection of basis pair and the data number in hash table bins.

In this paper, we consider similarity transformation. The main goal is to represent the feature points by a few of intrinsic parameters in a rotation, scale and translation invariant manner, this was done by defining an orthogonal coordinate frame based on the ordered pair of points (refer to basis-pair) from the point set and representing all other feature points with their coordinates in this local frame. Such a coordinate frame is defined uniquely by assigning coordinate (-1/2,0) and (1/2,0) to the first and second point respectively. Any similarity transformation applied to the point set will preserve their coordinates if they are represented in the same two-point basis. So if the two-point basis selected in the recognition phase is the same order as in the modeling phase, the coordinates of other points in the two local frames will be the same even if the object have undergone similarity transformations. In order to recognize partial occluded object, various basis-pairs can be selected, so even if some feature points was occluded in the recognition phase, other basis-pair can be used to compare the object with the model pattern. For recording the local frames, a hash table is used. For every ordered pair of model feature points the coordinate of other model feature points are computed in the orthogonal local frame defined by this ordered pair. Each such coordinate (after a proper quantization) is used as an entry to a hash table, where the basis-pair at which the coordinate was obtained and recorded. For different basis-pair, the coordinate may be the same, so every hash table bin will be a list of basis pairs. Here a hash table is a two dimensional table with bins recoding pattern shape information.

In the recognition phase, after the scene feature points are extracted, we choose an arbitrary ordered pair of feature points as basis-pair and compute the coordinate of other feature points taking this pair as basis. For each such coordinate, we check the appropriate entry in the hash table, and for every basis pair there, a vote is tallyed for it as corresponding to the selected scene basis-pair. If a certain model basis-pair scores a large number of votes, take it as a matching candidate and compute the similarity transformation between the scene and the model. If the current scene basis-pair does not score high enough, pass to another basis-pair in the scene.

In our study, we compare two sets of points in similarity transform invariant way. Two-point basis is used.

We make the shape matching by geometric hashing.

Preprocessing is executed as follows:

Step1: Extracting edge of the object as pattern feature points.

Step2: Define a reference frame using two chosen feature points. One of feature points is defined as the origin, and the axis is defined by the line between two feature points.

Step3: Compute the orthogonal basis associated with the defined reference frame.

Step4: Compute the coordinates of all the other feature points in the defined reference frame, constituting a reference frame system.

Step5: Use each coordinate as an address to the hash table, and store the entry at the hash table address.

Step6: Repeat step 2 to 5 for each pattern reference frame.

The matching of a target object is accomplished as follows:

Step1: Extract feature points in the scene.

Step2: For each reference frame of the target, compute orthogonal basis associated with this reference frame.

Step3: Compute the coordinates of all other points in the current reference frame.

Step4: Use each coordinate to access the hash-table and retrieve all the records.

Step5: “Vote” for the recorded pairs.

Step6: Compute the transformations of the "high scoring'' hypotheses.

Step7: Repeat step 2 to 6 for each target reference frame.

• III.    IMPROVEMENT OF GEOMETRIC HASHING

The complexity of geometric hashing is higher. If the number of model feature points is m, the modeling complexity will be O ( m ³). If the number of the feature points in the scene is n, the complexity of this recognition will be O ( n ³)[2].

Figure1. The flow chart of the proposed method of all possible basis-pairs will be large. Thus there will be a large number of local orthogonal frames. In this case, a large number of local coordinates have to be computed in every local orthogonal frame, some hash table bin’s list will be very long. Much time would be consumed to access it. We develop some techniques to improve the performance of geometric hashing method so that it can be used in real-time recognition applications.

Our improvements include the following several aspects. In the modeling phase, firstly, edge is extracted as the features of the model object. Secondly, the pattern is decomposed into some sub-patterns using clustering method to reduce the data number in hash table bins. Thirdly, the sub-patterns are recorded in a plurality of hash tables. In the recognition phase we improve the recognition performance by combining with image pyramid and edge direction information. Firstly, the edge is extracted by pyramid technique as the features of the coming image. Secondly, according to the angle and distance between the edge directions, the ordered pair of edge point is chosen. The flow chart of the proposed method is shown in Fig.1.

• A.    Image pyramid

The Object recognition task is usually accomplished by the whole image information. The more the number of pixels are on the image plane; the more accurate tracking performance can be expected. But at the same time more computations are required. Similar to human eyes tracking a fast moving car, it is not necessary to visualize a clear image to achieve the tracking mission. The tracking task can still be successfully executed although a vague image about the moving object is observed. Therefore, just rough image information will be sufficient for the initial stage of tracking. After the camera almost follows the moving object, more accurate tracking performance can be achieved by using an image with better resolution. This idea will be realized by the technique of image pyramid, which has also been implemented to resolve the difficulty of image correspondence for the correlation-based optical flow computation [8] and feature tracking [9].

The image pyramid is a data structure designed to support efficient scaled convolution through reduced image representation. Let us assume the size of the given image is N by N as shown in Figure2. The image pyramid is a hierarchical structure composed of n levels of the same image of different resolutions. At the bottom of the pyramid is the given full size image. Each set of neighboring pixels is replaced by their average as the pixel value of the image at the next level. This process, which reduces the image size by half, is repeated times until finally an image of only 1 pixel (average of entire image) generated as the top of the pyramid.

On the other hand, it is remarkable aspect that the process should be as fast as possible in visual systems. If we use only one hash table to record pattern, the number

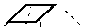
Level 0: lxl

Uevel 1: 2x2

Level 2:4x4

Level n: 2n x2

Figure2. Image Pyramid

In this way, we can obtain a sequence of copies of the original image in which both sample density and resolution are decreased in regular steps.

Figure3. Example of an image pyramid

An example of the image pyramid at two levels is shown in Fig.3. We combine both global and local information to detect edges while suppressing noise at the same time. A proper level is found in the pyramid where noise is sufficiently pressed while major edges are still represented. For each edge element, a pixel with its gradient greater than a threshold, search its 4 children in the next level to identify finer edge elements. We do this recursively until finding edges with fine details but without interference of noise.

• B.    Pattern clustering and a plurality of hash tables

In order to improve the modeling and recognition efficiency without reducing the feature points, we consider reducing the number of possible basis-pairs and the number of coordinates to be computed in the local frame defined by the basis-pair. We perform the following algorithm for this goal. The pattern first is decomposed into some sub-patterns using clustering method. Second, different sub-patterns are recorded in different hash tables. Third basis pairs are selected only on the same sub-pattern, and then local frame coordinates of the feature points are computed only on this sub-pattern. The computed coordinate is used as an entry to the corresponding hash table.

Let us make a complexity analysis. Since we only need to select basis pairs on the same sub-pattern, and local frame coordinates of the feature points are computed only on the sub-pattern, this method not only can greatly reduce the number of possible basis-pairs, but also the computation of local frame coordinates can be cut down. Also, the length of basis-pairs list in hash table bins can be shorted.

If the number of the original pattern’s feature points is m, a sub-pattern average has n feature points, the number of decomposed sub-patterns is k, and then the time complexity for our method will be 1/ k ² that of the present method . This greatly reduced the computation time.

For basis-pair ( O ₁ , O ₂ ) in scene, if the pattern basispair ( P ₁ , P ₂ ) obtained a large number of votes, one object pose ( X , y , 0 , s ) can be obtained by comparing the length, angle and location of the two line segments.

Obtained all possible poses, we define a metric in pose space and use clustering method to obtain the object poses. We check the poses by edge points and refine the poses using the least square method.

——

The local frame coordinate ( X _ij , Y _ij ) is computed using (1) and (2).

X» = (Pj-Po )/IIP," Po| 1= (Xj , y, )

—

Yij = -(yij, x, )

Where, (Pi,Pj ) is any given basis- pairPo = (Pi + p )/2 .

The coordinate of any other feature point P_f in this frame is computed using (3).

( X f , y f ) = ( X j • ( P f - P o ), Y j • ( P f - P o ))       (3)

The coordinate is used to record the basis-pair of the hash tables in the modeling phase. It is also used to access the hash tables to vote the pattern basis-pair corresponded bins in the recognition phase.

• C.    image alone edge direction and basis pair selection

The other methods also can be used to speed up the modeling and recognition phases. If the number of feature points is less, the number of possible basis-pairs will be less. Thus the computation time of local coordinates for all feature points can be cut down. We have reduced the number of edge points and the number of basis-pairs using image pyramid. Another significant improvement of this paper is that a good local constraint is used to increase the recognition performance. On the other hand, how to incorporate local information into GH is important for increasing the matching efficiency. Basically, good local constraints can increase both accuracy and the speed of matching by removing irrelevant hypotheses. Pairs (object, basis) whose bases are not similar to the scene basis should not be counted in the voting stage. Using this constraint, the number of spurious hypotheses can be considerably reduced.

In the recognition phase, the search range first is limit based on the sub-pattern’s information. In the limited range, the basis-pair is selected and the scene local frame coordinates are computed. Feature pair points with distance larger than the maximum diameter of subpatterns will not be selected as basis-pair to vote any subpattern.

sub-pattern

• Figure4. This constraint is used in the recognition stage

The example is implemented as shown in Fig.4. In this way, the number of possible basis-pairs is reduced in the recognition process. For every selected basis-pair, if the local frame coordinates of the feature points is outside certain range, since it do not score to any sub-pattern, it need not to be computed to vote. Also, the number of the local frame coordinates computed can be reduced. Therefore, the recognition phase can be speed up.

So, we select basis-pair by limiting the angle size. If the angle is not in some range, they will not be selected as basis-pair.

To summary, the modeling and the recognition procedures of our work are as follows:

Modeling phase:

Step1: Detect the pattern image edge and resample edge by pyramid technique.

Step2: Decompose the pattern edge into some subpatterns by clustering method.

Step3: For each ordered pair of edge point on same subpattern, if the angle between the edge directions of the pair is in certain range, the following a) and b) are implemented.

• a)    Compute the local frame and the local frame coordinate of other edge points on the same subpattern.

• b)    After a proper quantization, use the coordinate as an index to the corresponding hash table and insert into the hash table bin. Where, the information of the basis-pair was used to determine the coordinate.

Recognition phase:

Step1: Detect the coming image edge and resample edge by pyramid technique.

Step2: Choose the ordered pair of edge point in the image. If the angle between the edge directions of the two edge points and the distance between them are in certain range, the following operations are executed.

• a)    Compute the local frame and the local frame coordinate of other edge points which are in certain neighbor range of the basis-pair.

• b)    Appropriately quantize the coordinate, access the bins of all hash tables, and for every entry there, cast a

vote to the pattern basis-pair, then determine the pattern basis-pair that maximum the scores of all pattern basis-pairs in the plurality of hash tables. If its scores are high enough, compute the pose.

Step3: Find the appropriate poses by clustering, check and refine the poses using pattern and scene image edge points.

• IV.    Experiments and Results

In this subsection, we perform a series of detection experiments using the proposed algorithm and different images. The test environment is 2.8GHz CPU with 512M memory and VC++6.0. Both visual and quantitative evaluations are presented with implementation of this technique in images. We show three experiment examples. The first example is implemented using a black-and-white image. The size of this image is 512 X 480. This image includes four cases of the recognition object: the original object, the rotated object, the partial occlusion object, and the scaled object. The first experiment results are shown in Fig.5. The experiment results have shown that the object can be found accurately in any cases. The search time is about 60 ms, including edge detection, vote, pose clustering and pose refining. Where vote time is less than 10ms.One pattern and one hash table are used in this example.

Figure 5: rotated, occluded and scaled object detection

The second example is implemented using a real image as shown in Fig.6. This is a character string pattern detection sample. Character string can be recognized accurately using this method. The total search time is about 90ms, the vote time is less than 12ms. We use four sub-patterns to represent two characters and four hash tables in this sample.

The third example is done on a color pattern search. The objects have different size, different angle and different color as shown in Fig.7. After detecting edges in the color image, we detect objects in the scene by the presented method. The experiment results are shown in Fig.7. As be seen, these objects can be recognized also accurately. The total search time is about 65ms, the vote time is less than 2ms.

In addition to precise recognition, we add the denoting step in image preprocessing. In this study, the denoting step and edge detection [7] are accomplished based on Vision Software Library developed by Fast Corporation, Japan.

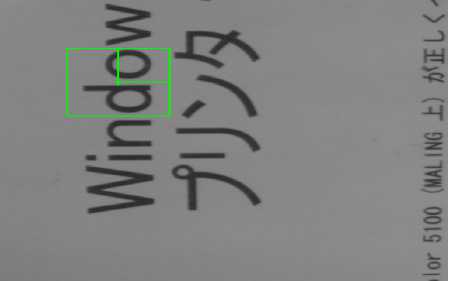
Figure6. Character string pattern detection

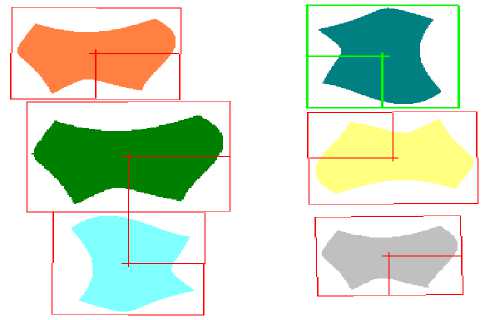
Figure7. Color object detection

• V.    CONCLUSION AND FUTURE WORK

In this paper, in order to fulfill the requirements of real-time industrial applications, we have developed a fast object detection technique in images based on geometric hashing. With implementation of this new technique to various images, results have shown to be successful for fast object recognition. Both complexity analysis and experiment evaluations have demonstrated the efficiency of this technique. Future work will concentrate on further improving this technique to fulfill the requirements of real-time industrial applications and detection of irregularities on medical images.

Acknowledgment

Thanks to all members belonging to the Image Solution Group of Fast Corporation, Japan.