An improved multi-objective BPSO-based method for radial distribution networks reconfiguration

Transmission of electrical energy is the most important task of distribution systems and due to the yearly growing of consumers’ loads; these networks will become larger and more complex. Most of distribution networks all over the world are radial and every consumer is fed just from one side. Since these distribution networks are complex and also many plants have been made, it can cause different states for the consumers’ feeding. But there are a lot of switches in distribution networks which can change the structure of the network. These switches can be divided into two categories including sectionalizing (normally close) switches and tie (normally open) switches. Change in the structure of network by altering status of its switches which called reconfiguration or restructuring, not only determine the type of consumers feeding but also has more applications. Some of these applications include load balancing, minimizing total losses of system and improving voltage deviation and reliability of network. Utterly reconfiguration is useful when some faults occur in the network. This activity minimizes de-energized loads after faults. So the existing switches are used for both management and maintenance, but the existing paper focuses only on system management. Some other applications of network reconfiguration include increasing capacity of network, reconfiguration with fewest switches, system development, finding optimum place for distributed generation (DG), etc. that are not the subject of the study here. Since there are a lot of switches in the network, reconfiguration issue is a complex optimization problem which has a lot of limitations. Some of these limitations are

Recently, reconfiguration has been carried out by practical experience of operators, but today operation of distribution networks is an engineering challenge, because optimal solution is always considered and due to mass and complexity of these problems, the only possible way is to use specialized software. The main goal of optimization is minimization of costs and improving services. There are a lot of methods for reconfiguration which has advantages and disadvantages. Already many literatures studied reconfiguration problem and a lot of methods has been applied on it. The results of these studies provide acceptable solutions. Reconfiguration problem was first considered in [1] in order to minimize total losses by a heuristic and hybrid optimization algorithms. In [2] reconfiguration was done by branches changing. This heuristic method closes one switch and opens the other switch, then calculates the network losses. Changing the status of the switches can be done by a lot of algorithms, but since power system problems are combinatorial optimization, they are difficult to solve by traditional linear or nonlinear methods [3]. Authors of recent literatures use optimization methods such as genetic algorithm (GA) [4, 5], fuzzy systems [6, 7], bee colony (BC) [8, 9], simulated annealing (SA) [10,11], Tabu searches [12,13], heuristic algorithms (that are not in the scope of this paper) [14, 15]etc. Recently PSO algorithm is considered in [16, 17], because it has some advantages ,namely, simple structure, good speed and high accuracy. This paper uses this algorithm, too.

One more important issue in the reconfiguration problem is objective function. The most important objective in the recent literatures is loss minimization. But there are more objectives which can be considered, too, such as reliability [17], voltage deviation [18], load balancing [19], transient behaviors of the network [20] and smart grid interactions [21] and so on. Usually one or two objectives are optimized simultaneously but some times more than two objectives are considered as optimization [22]. This paper optimizes four objectives including load balancing, total losses of network, voltage deviation and system reliability.

Bpso algorithm

Recently, PSO algorithm has previously been used at many literatures for reconfiguration problem and has a known structure. This algorithm is based on the social behavior of birds (particles) flocking looking for food. Answers of considered problem can be represented as a particle. At first the particles initialize randomly. Then every particle will change its position based on the best searching experience of individual (P best ) and the best searching experience of population (G best ). When P best and G best are obtained, every particle updates its position by:

v £f^w = ^wvid + ^ci x ^and() x (Pbest - x_id) + c₂ x rand( ) x (Gbest - X id)

new _     । ^n.^v xid = xid + vid

Where v_id is the original velocity of the i^th particle, v_id^new is the new velocity of the i^th particle, w is the inertia weight, c 1 and c 2 are the acceleration constants, x id is the previous position of the i^th particle, – 618 –

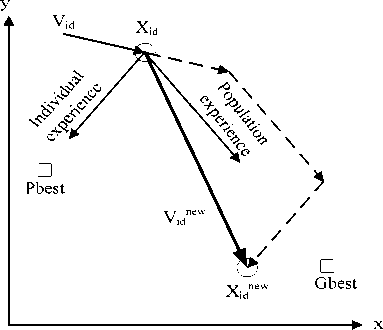
Fig. 1. Updating a particle position in PSO xidnew is the new position of the ith particle and rand( ) is a random number ranging between 0 and 1. Fig. 1 explains how particle positions is updated.

Reconfiguration in the above mentioned form is a binary problem. For this reason, binary version of PSO (BPSO) should be used. In BPSO algorithm a sigmoid function (3) is used for position updating.

WD =

1 + е

... new ~^v id

Position update at PSO is done in two stages. At first particle velocity is updated by (1). Then with (2) sigmoid function is calculated and finally new position is obtained by (4).

IF (rand() < S(v^ THEN ./ = 1 ELSE x^^w = 0 (4)

New calculated particles positions may be inappropriate. For example, due to loss of radial structure of the network, some loads will be de energized. So feasibility of generated codes should be verified. Already some methods were introduced to check these codes everyone whereof has advantages and disadvantages. This paper proposed a new simple and effective way to update particles positions.

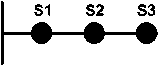
The first step to solve reconfiguration problem is representation of network structure with a comprehensive code for computer. To show the status of N switches in a distribution feeder a string of N bit can be used. For each switch, ‘1’ shows considered switch status is closed and ‘0’ shows it is open. For example, for the feeder shown in Fig. 2 the above mentioned code is (1 1 1 0 1 1 1 1) [23].

Then the problem is to find optimum code for the network which results in minimum value of the objective function, for a distribution network with N switches there are 2N possible codes which all of them are not necessarily appropriate. Eliminating inappropriate codes solution space will be reduced significantly.

The main idea of this paper is a new method for particles position updating. At the first step, an appropriate code is considered and updated normally. Then the feasibility code is checked. For the appropriate codes the algorithm will be continued. Inappropriate codes will be updated again by (4).

Feeder 2

Feeder 1

S4 S5 S6 S7 о • • •

S8

Fig. 2. Simple structure of a network

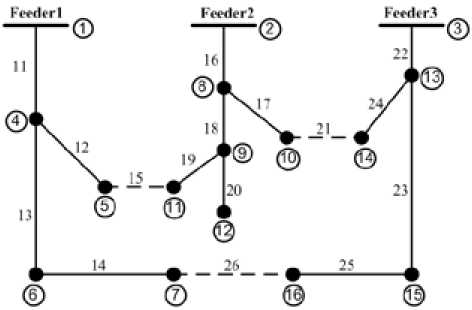
Fig. 3. The3-feeder distribution network used for simulations

This procedure should be continued until the updated code become one of the possible codes. This method has not only a good speed, but also perfect accuracy. It is clear that generated codes certainly are one of the appropriate structures of network. The distinction of possible structures is an easy method too. There are three methods of making distinct codes that will be explained at following paragraphs. All methods are implemented by logical instructions.

• -    The First method: Generate a random binary code and restructure the network by it. If all buses are fed just from one side, this code is appropriate; otherwise, it isn’t. The speed of this method is low.

• -    The Second method: Fig. 3 explains this method. Here the network has three feeders and it is obvious that there must not be any closed loop between them, and all buses must be fed too. So all connection ways between feeders should be found and every relative code must have just one 0, else that code is inappropriate. The other important limitation is that switches of loads or feeders should be 1. To explain this method, see Fig. 3. Connection ways between feeders include down branch (codes 13, 14, 26, 25 and 23), left branch (codes 12, 15, 19 and 18) and right branch (codes 17, 21 and 24). In every above three codes there should be just one 0 to meet network structure feasibility. All appropriate states of network are equal to multiplication of the number of all collected codes. For example in Fig. 2 the number of appropriate codes is 60, this number is gotten from the multiplication of five down codes (13, 14, 26, 25 and 2 1 3) by four left codes (12, 15, 19 and 18) by three right codes (17, 21 and 24). This method is harder but very faster and reliable.

• -    The Third method: Desired codes can be generated manually or by Microsoft Office Excel and saved in a database. This way is not automatic but is very fast.

Most important advantage of this method is its simple structure, because other similar methods are very difficult and presumably low speed (due to complicated calculations) [23, 24].

Reconfiguration process

Reconfiguration process needs a fast and accurate load flow method to evaluate objective function. In this paper the well-known forward/backward load flow methods is used [2]. Then this method has been rewritten in MATLAB® and become the principal of the work. Then forward/backward load flow is done to find all bus voltages and power flowing through all sections. Then the value of objective function is calculated and sent to BPSO algorithm. BPSO algorithm is repeated to meet the desired convergence.

The objective function

The objective function used in this paper has four weighted components including: load balancing, total losses of network, voltage deviation and system reliability. It is shown as following:

Objective Function

= a.Loss + р. Voltage Deviation

+ y. Reliability

+6. Load Balancing where α, β, γ and θ are weighting coefficients which show relative importance of the components. These coefficients are obtained with historical experiences and strategies of each distribution system company. In this paper they are chosen 1, 2, 0.0015 and 31respectively. Total losses and cumulative voltage deviation will be obtained by equations (6) and (7).

Lo s s = '<             pu                                                      (6)

Vo lt age d eviation = L^vVi — 1)² pu                                  (7)

where Viis the voltage magnitude of the ith bus and Pi, Qi, and riare the active and reactive power and resistance of the ith section respectively.

In this paper reliability of distribution networks are taken into account by system indices. For each load center an average failure rate (λ in #/year), an average repair time (r in hours), and an average outage time (U in hours/year) can be calculated [25], where:

U = A.r(8)

The system reliability indices used in this paper are System Average Interruption Frequency Index (SAIFI) and System Average Interruption Duration Index (SAIDI). They can be obtained by the following equations:

SAIFI = 12j^i(9)

IWi

SAIFI =^^_(10)

‘

Where N i is the number of customers at i^th load point. Reliability is evaluated by equation (11). Also, considering different weighting factor (γ₁ and γ₂ instead of γ) for SAIFI and SAIDI is possible.

Reliability = SAIFI + SAIDI

Reliability parameters for considered system are listed in the paper appendix.

Load balancing component will be obtained by the following equation. I i is total current magnitude of the i^th feeder.

Load Balancing = S ?Li S }=i Ik - kl

Simulation and results

For a well-known distribution network shown in Fig. 3 which has been used in many previous researches, the proposed method was applied. Network parameters can be found in [18]. This network includes 3 main feeders, 13 tie switches and 3 sectionalizing switches. Its nominal power (Sb) is 100MVA. Fig. 3 shows original condition of the network, at these 15, 21 and 26 state switches are open and other switches are close. To show the speed and effectiveness of the proposed method, a comparison is made between this method and three other well-known algorithms. Table 1 shows reconfiguration CPU times to minimize load balancing, total losses, voltage deviation and reliability of the network by four methods. All algorithms converge to the same solution. It is clear that running time for the proposed method is much lower and if the network busses increase, the CPU time difference will be obviously more.

Conclusion

This paper proposed an improved BPSO algorithm for radial distribution networks reconfiguration which applies a new method to update swarm position. It is not only simple and fast but also has high

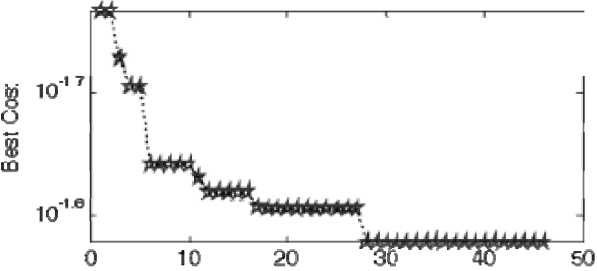
iteration

Fig. 4. Convergence curve of the proposed method

Table 1. Simulation results for proposed method and three other algorithms

Algorithm Solution (open switches) CPU time Population BPSO 17, 19 and 26 1.01 4 ACSA [18] 17, 19 and 26 1.81 5 SA [18] 17, 19 and 26 2.07 500 GA [18] 17, 19 and 26 2.32 5 accuracy. The objective function has a four weighted component including: load balancing, total losses of network, voltage deviation and system reliability. Test network was a standard network by 3 feeders and 16 switches. Comparison of the proposed method with three well-known algorithms shows its better efficiency.

Appendix

Table 2. System indexes of the test network

r	λ	Section	r	λ	Section	r	λ	Section	r	λ	Section
4	0.18	15-16	4	0.16	9-12	3	0.16	2-8	2	0.15	1-4
3	0.18	5-11	2	0.15	3-13	4	0.16	8-9	2	0.15	4-5
2	0.14	10-14	3	0.15	13-14	4	0.16	8-10	2	0.15	4-6
4	0.14	7-16	2	0.15	13-15	4	0.16	9-11	3	0.14	6-7