An Individualized Face Pairing Model for Age-Invariant Face Recognition

The human face is undoubtedly a very informative part of the human body which has been described as the most suitable for biometric recognition because of its non-intrusive nature and the fact that it can be captured from a distance with or without the cooperation of the subject [1, 2]. Face recognition technology has become a prevalent part of most applications and devices. Organizations such as Facebook and Google use face recognition to improve user experience and security. This development is traceable to the success of face recognition research which dates to about 50 years ago [3] and has since improved tremendously.

Face recognition is one of the twin modes in which face recognition biometric systems operate, namely verification and recognition [2]. In face verification, given a face, we want to confirm if this person is who he claims to be. Thus, this is a one-to-one matching and is often used to authenticate a user for access to some secured domain. Face identification or recognition, on the other hand, involves one-to-many matching [4]. In face recognition, we are given a query face and try to see from our database of enrolled faces, which face has the closest match to the query face. Thus, in the case of face recognition, there could be more than one possible match at different levels or scores, and the face with the highest scoring match (often called, rank-1 ) is returned as the matched face. Agreeably, the correct or incorrect face can be returned as the top-matching face depending on the accuracy of the face recognition algorithm and there are many factors that impact this accuracy including variations in head pose, illumination, facial expression and ageing among other factors.

Of all the mentioned factors, ageing seems to be the most difficult to handle and this is confirmed by the level of accuracy yet reported for age-invariant face recognition systems [5]. Ageing is particularly difficult to handle because of its uncontrollable, irreversible, personalized and non-linear nature. Variations in facial expression, head-pose and illumination can all be handled by obtaining images within controlled environments. In the case of ageing, however, enrolled faces often have to be recaptured after a number of years to avoid missing such faces at matching time. This limitation, can thus be exploited by suspects and criminals to bypass face recognition systems. Thus, an individual enrolled on a face recognition system at age 18, will likely go unrecognized by the same system at age 30 if such system thus not keep track of age variations.

This work therefore presents an age-invariant face recognition (AIFR) system to improve face recognition in the presence of age variations between query and enrolled faces. The developed AIFR model leverages on the individualized nature of human ageing to develop an individualized face-pairing model to represent the relationship between a query face and those of known individuals at different ages. This relationship is then used to build a representation for the query face which can be matched against enrolled faces at different ages in order to improve the matching score of the correct face/individual to which the face belongs.

The rest of the paper is organized as follows. Section 2 discusses previous related publications on AIFR and points out their general limitation which this work combats. Section 3 presents the methodology employed for this research. Section 4 discusses the experiments carried out and section 5 concludes the paper indicating future directions of the work.

2.    Related Works

According to [6], AIFR research can be broadly classified into two – the Generative and Non-generative methods. In the generative methods, appearance-based transformations are introduced into a test image in order to reduce the differences (due to ageing) in facial appearance between age-separated images of an individual. Non-generative methods, on the other hand, derive age-invariant features from faces and use these features to perform face recognition across ages. It is noteworthy that while most recent AIFR systems are non-generative, the earlier systems were mostly generative. In this section, we review the generative as well as non-generative methods.

Some of the earliest published AIFR works were those of Lanitis and Taylor [7, 8] and Lanitis et al. [9]. In their work, learned age transformations were used to model aging effects on faces considering, the personalized aging variations. The aging variations were isolated and simulated using Active Shape Models (ASM) [10] and an aging function was modelled to represent the age of a given face. The work of Lanitis et al. [9] was reported to achieve 71% accuracy on a dataset of 165 face images. A Bayesian age difference classifier built on a probabilistic Eigenspace framework was also proposed in [11] to tackle to the problem of age-invariant face recognition. Experiments on ‘Point Five’ faces of individuals in the passport database of facial images gave mean accuracy of 72%. In [12], a two-fold approach was proposed for modelling facial aging in adults. Their model consisted of a facial shape transformation model and a gradient-based texture transformation model to capture facial shape and textural variations. Face recognition accuracy (rank-1 accuracy) on the FG-NET dataset [13] was 51%. Also, a 3D morphable model was developed from 2D images to capture facial aging variations [14, 15]. At training and testing, facial images were modified to account for the age-induced variation using a 3D model deformation and texture modification before matching the face images. Rank-1 recognition accuracy of 37.8% was reported on the FG-NET dataset. All the above methods employed a generative method of dealing with AIFR. The next paragraph discusses more recent works which employ non-generative methods.

In [16], a Multi-Feature Discriminant Analysis (MFDA) framework was developed to use high dimensional features generated from local descriptors. Using fused multiple Linear Discriminant Analysis (LDA) classifiers, Rank-1 accuracies of 47.9% and 83.9% were obtained on MORPH [17] and FG-NET datasets. Juefei-Xu et al. [18] used the periocular region of the face (upper part containing the two eyes) to recognize faces in the presence of age variation. 100% rank-1 recognition accuracy on FG-NET dataset was reported. Although, attaining 100% classification accuracy seems a noble achievement, the question of the generalization performance of this method, especially on other larger datasets (e.g. MORPH, CACD), quickly comes to mind. In [19], the geometric representation of the facial shape was modelled in a Grassmann manifold and passed to a Support Vector Machine (SVM) classifier. Their model was tested on 272 images of 62 subject from FG-NET, generating 665 intrapersonal pairs and about 6000 extra-personal pairs with 3-fold cross validation obtaining an EER of 23.6%. A Hidden Factor Analysis (HFA) approach was proposed in [20] as a probabilistic model which captured age-specific and identity-specific information as two latent but separate variables – an age-invariant identity factor and an age factor affected by the ageing process. The HFA model obtained 91.14% and 69% recognition rates on MORPH and FG-NET datasets respectively. A cross-age reference coding (CARC) scheme was developed in [21, 22] for age-invariant face recognition. The CARC assumes that if the faces of two different individuals look similar at a particular age, these individuals should also look similar at adjacent ages. The CARC approach achieved recognition rate of 92.8% on MORPH and 83.4% accuracy on a cross-dataset setting in which they used images from CACD for reference and tested on the MORPH dataset. On CACD validation set, their CARC approach achieved a recognition rate of 87.6%. [23] proposed a joint-task learning model for coordinating the tasks of facial age estimation and age-invariant face recognition. Their method ensured that age and identity features were separately learnt for the two tasks and their interference is avoided as much as possible. EER of 19.4 and 5.5 were reported on FG-NET and MORPH datasets respectively. In [24], triangle features consisting of the coordinates of the two eyes and the nose were used to model the face, these geometric features were combined with facial texture features obtained from Active Appearance Models (AAM). Their model achieved classification accuracy of 97.56% with k-Nearest Neighbour (KNN). Li et al., [25] developed a local patterns selection algorithm for extracting low-level discriminatory features from image pixels. Their model achieved 94.87% classification accuracy on MORPH album II dataset. Local Binary Patterns (LBP) and Histogram of Oriented Gradients (HOG) features were used within a probabilistic LDA classifier in [26] to achieve classification accuracy of 88.23% and 95.62% on FG-NET and MORPH datasets respectively.

More recently, deep learning models have been proposed to address the AIFR problem resulting in a leap in recognition accuracy. Various deep learning architectures were proposed in [27-32] for extracting age-invariant identity features from the face for AIFR.

It can be observed, that over the years, the AIFR classification accuracy has been lowest on the FG-NET dataset, even though it is relatively smaller than MORPH and CACD datasets. Also, considering the fact that CACD is the newest of these three popular AIFR datasets, classification accuracy on it has already exceeded 99%. However, classification accuracy on FG-NET – the oldest of the three datasets – is still generally below 95% except for a few works which report more than 95% accuracy. This difficulty on the FG-NET dataset can be traced to the poor quality of images in the dataset as many of the images were scanned pictures some of which had been worn out or somehow mutilated, whereas the images in MORPH, for instance, are all high-quality frontal images. Interestingly, these poor performances on FG-NET dataset is not only caused by the small size of the dataset as several of the deep learning models discussed above were often trained on the larger datasets with FG-NET only being used for validation. We believe that a major difficulty in obtaining excellent AIFR results on FG-NET compared to other datasets is the large age gap in the FG-NET dataset coupled with the small size of the dataset, thus there are not enough images to learn the large variations in ages between individuals. While FG-NET images have an average age range of 45 years per individual, MORPH has 4 years and CACD has 10 years.

We have also observed that most previous AIFR models were evaluated using a subset of the datasets involved in order to create matching and non-matching pairs. So, some face pairs would have been left out during evaluation. While it is quite difficult to obtain all possible face pairs from a dataset as this would mean m × ( m – 1) face pairs, where m is the size of the dataset, in this work, we explored all possible face-individual pairs in order to capture all possible combinations of different non-matching individuals for AIFR, i.e. m × n pairs where n is the number of individuals in the dataset. The proposed model also proves useful for use with small datasets and shallow learning methods since it can help generate larger sets of face-individual comparisons for training.

3.    Method

Age-invariant face recognition (AIFR) refers to the task of determining whether a pair of different age-separated face images belong to the same individual or not. Thus, it is a binary classification problem. However, the number of matching and non-matching face pairs that could be constructed is huge depending on the size of the dataset. This, along with the extent of age variation in face images of an individual, makes AIFR a challenging task as recognition becomes more difficult to with wider age gaps between any two faces under comparison.

Existing works have attempted to solve this problem by creating several pairs of face images from the same individual (called intra-personal pair) and face images from different individuals (called inter-personal or extra-personal pairs), but definitely not an exhaustive set of all such possible pairs and many such times, the pairs are created randomly. Here, a method was designed for automatically collecting all the possible intra-class and inter-class pairs within a dataset and the computed distances between the pairs were used to train a classifier to determine whether face image pairs belong to the same individual or not. This, of course, has the advantage of increasing the amount of data available for learning and also providing the possibility of using balanced classes of data to train the classifier.

However, to prevent an explosive growth of the number of face pairs available for training and to also be able to capture the representations of the different images of each individual at once, our face pairing method is not a face-to-face pair, but face-to-individual pair. Thus, instead of matching the feature vectors of two face images in a pair, we match the feature vector of each face image to the feature vectors of face images of individuals and obtain a similarity measure from the vector-to-matrix pair. Therefore, for a dataset with m face images and n individuals, this results in n × m pairs. Then these pairs are used for similarity scoring, generating a similarity score vector for each face-to-individual pair.

Subsequently, there are enough pairs (matching as well as non-matching pairs) to learn the consistent identity features across the age-separated faces of an individual. Every face image is paired with its own individual (matching pair) as well as with every other individual (non-matching pair). Since each face image can belong to one and only one individual, it means that there is only one matching pair and n-1 non-matching pairs for each face image.

Then, for each face image, the final feature vectors used for learning are the similarity score vector of its matching pair along with the similarity score vectors of each of its non-matching pairs taken one at a time in successions, thus yielding a balanced set of matching and non-matching pairs for age-invariant identity learning. At training or testing, the final class of an input image pair is then determined by the most frequent class predicted for the set of matching and non-matching pairs presented. Figure 1 shows the individualized face pairing model described above.

In this work, the AIFR problem is formulated as follows:

Definition 1: Suppose we have a set A of face images and a set B of ages, the following definitions hold

A = { a. | i = 1,---, m }

B = {bj l j = 0,—>qa vj j >bj} where ai = a face image; bj = an age class or age value; m = number of face images; q = the highest age class or age value

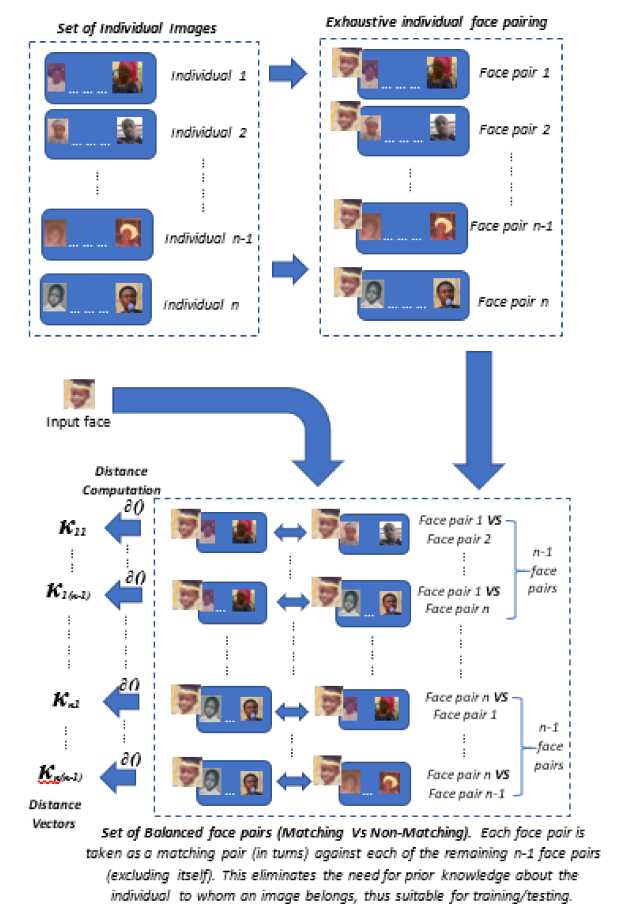
Fig. 1. The Individualized Face-Pairing Model

Definition 2: Given the sets A and B as defined in definition 1 and a set D of unique identities of individuals whose face images appear in A at different ages as given in B , then D is defined as follows:

D = { d _y\Y = 1,..., n }

where d_γ = a unique label identifying all images of a particular individual and n = number of individuals .

Definition 3: We define a function f 7 , a one-to-many mapping between the sets A and D as follows:

Precisely,

f7 : A→D f7(ai)=dγ

Since images are dealt with as embeddings, then equation (5) can be rewritten as in (6), where X i is the embedding (feature vector) of image a i .

f 7 ( X i ) = d γ

f 7 maps each image in A to its unique individual identity in D . Thus, every image is being mapped to the individual whose face is displayed in the image. Thus, all images in A , which are mapped to the same individual label in D are different [age-separated] images of the same individual. For each face image, X i is obtained for different face regions as discussed in [33].

• 3.1.    Face-Individual Pairing

Each image can match exactly k-1 images (suppose k is the number of images in A belonging to an individual) and, in practice, this differs from one individual to the other allowing for different number of possible matching pairs for each image. This creates a huge amount of data with huge imbalance. Even if we try to balance this by creating k-1 nonmatching pairs for each image, the overall number of classes could still be imbalanced and a large number of possible non-matching pairs could be left out. To solve this, all k images of an individual are taken as a single entity to be matched against each image, since at this point, each image is simply an embedding (a vector of features). This does not only limit the generated pairs to a sizable number, but also allows balance to be achieved within the data as earlier explained. With this method, each image will have exactly one matching pair (since every image belongs to one and only one individual) and n-1 non matching pairs. These multiplies the size of data by the number of individuals whose images are in A , or simply the cardinality of D which is n .

Definition 4: Given the sets A and D as defined in definitions 1 and 2 respectively and the mapping f 7 as defined in definition 3, then we define a set A pair , of image pairs, a set D pair of classes (matching and non-matching) of the image pairs in A pair and a function f 8 which maps A pair to D pair as follows:

A_pair = {( a_i , E _γ ) _j | i = 1... k ; j = 1... q } (7)

Equation (9) can be rewritten as

D pair = { ρ j | j = 1... q }

f : A → D

8        pair           pair

f 8 (( a i , E γ ) j ) f 7 ( a i ) = ρ j

where

• ( a , E ) is a tuple consisting of an image a i and a set E γ of images belonging to an individual γ ; thus, Eγ A and k is the number of images of individual γ .

ρ j is the corresponding class (matching or non-matching) of the tuple ( a , E ) .

Since, A pair is actually constructed from the image features and not the images themselves, the tuple ( a , E ) can be rewritten precisely as

( X_i , Γ _γ ) _j

where

X i is the feature vector of image a i and Γ γ is the matrix of feature vectors of all images in A of individual γ . Thus, equation (7) and (10) can be rewritten as follows:

A pair = {( X i , Γ γ ) j | j = 1... q } (12)

f ₈(( X_i , Γ _γ ) _j ) f ₇( X_i ) = ρ _j (13)

Equation (13) is a composition of functions f 7 and f 8 . While function f 7 retrieves the original identity label of an image, f 8 converts this identity label to a class indicating whether the said image is in a matching or non-matching pair in the tuple ( X , Γ ) .

The resulting sets A pair and D pair are of cardinality m × n ; m being the number of images in A and n being the number of unique individuals whose images are in A (definition 1 and equation (1)). With one matching pair and n-1 non matching pairs as previously explained, the resulting data in A pair is quite imbalanced and non-matching pairs far outnumber matching pairs by a factor of m × (n – 1) . At first, this looks like a problem, but it amazingly provides us enough data to create balanced classes in multiple stages as described shortly and thus improve the predictive power and generalizability of our model.

• 3.2.    Data Balancing

  Data imbalance is a major drawback of most learning tasks as the learning algorithm tends to make most of its predictions in favour of the most represented class. An attempt to balance a given unbalanced data would therefore be worthwhile. To achieve data balance with the data available in A pair and their corresponding classes in D pair , all matching pairs are taken in turns with each of the n-1 non-matching pairs to generate n different sets of matching and non-matching pairs of images. In clearer terms, suppose there are 100 images of 10 different individuals; then m = 100 and n = 10 . The resulting A_pair will be of size 100 × 10 containing matching and non-matching image pairs. Precisely, there will be only 100 matching pairs constructed from each image and its own individual and 900 non-matching pairs constructed form each image and the nine (9) other individuals. Thus, a new set of balanced data can be extracted from A pair by selecting the 100 matching pairs along with the non-matching pairs created from the first individual, the second individual and so on. So, each new set of image pairs consists of 100 matching pairs and 100-x non-matching pairs (where x is the number of images of the individual being used to select non-matching pairs for this new set). Assuming the first individual is being used to select non-matching pairs, and there are seven (7) images of this particular individual, then the resulting new set extracted from the 1000-sized A_pair will include all 100 matching pairs plus the 93 non-matching pairs obtained by comparing all the other 93 images with the first (that is γ =1; from equation (3)) individual. This is much balanced than having 100 matching pairs against 900 non-matching pairs. And this is done for every γ , so that in the long run, there are n different sets of matching and non-matching image pairs – one for every individual whose image is in A .

To create a completely balanced set of image pairs with the same number of matching and non-matching pairs, the following is done. For every individual whose images are used to select non-matching pairs, the non-matching pairs obtained for each image of this individual via the next individual to it (either to the right or the left) is selected. Eventually, for each matching pair, there are n different sets of non-matching pairs. With this method, for every face, there are n different sets of data features of matching and non-matching pairs to be used for training/testing and in the long run, the most frequent of the n different learnt/predicted classes is selected as the final class of the face. The face pairing algorithm is detailed in algorithm 1.

Definition 5: Given the sets A_pair and D_pair , a balanced set of image pairs A_bal with their corresponding classes D_bal is constructed as follows:

bal         i , γk        i , γ)k | k = 1...m}(14)

Dbal ={ρr |r=1...n}(15)

f9 : Abal → Dbal where

(X ,Γ ) represents a matching pair and (X ,Γ ) , a non-matching pair. Thus, the indices γ and γ in equation (14) i       γi                                                                                                        i       γi                                                                                                                              ii represent the individual whose image embedding is Xi and another individual (subject) whose embedding is X respectively.

However, to ensure that a matching pair is not selected twice, i is used to show that whenever γ= γ then γ is used instead.

For each matching or non-matching image pair, similarity scoring was done by computing distances between the feature vectors to obtain a final feature vector as a concatenation of the original feature vector X_i and the distance vector. This final vector is what is supplied to a classifier to classify image pairs as either matching or non-matching, thus achieving AIFR. Similarity scoring was done for the entire image pairs before data balancing and distance computation was done for each face region and eventually concatenated from all face regions to form a single vector for each face pair. For similarity scoring, we used the Hamming distance [34] to obtain similarity scores between face embeddings and individual embeddings.

4.    Experimental Results 4.1.    Datasets

To investigate the performance of our individualized face-pairing model, we performed experiments on two public facial ageing datasets, namely FG-NET [13] and CACD [21] and one dataset collected for the purpose of the study, FAGE. The statistics of the datasets are presented in Table 1. The FAGE is a dataset of 540 indigenous African face

Algorithm 1: Face Pairing algorithm

Input: Input image features (Xi), training data features (trData), training data individual identity labels (D), number of facial regions present in input features (numRegs), Distance computation method (distMethod)

Output : Similarity scored face-pair features ( A_pair ), Matching vs non matching reponse label

( D pair )

1. // Note the indices of each individual 2. numIndv = size( unique(D) ); // Get the number of unique individuals 3. // Get the start and end indices of each unique individual 4. ai = getIndvIndices( D, numIndv ); 5. rowSz = numIndv; // size(Xi, ‘rows’)* numIndvs = numIndvs 6. colSz = numRegs; 7. lastCol = size(trData, ‘cols’); 8. numFtrs = lastCol / numRegs; // this must be divisible 9. y = 0; // flag for matching / non-matching pairs 10. // initialize empty arrays for the new features and their response labels 11. newData = initArray( rowSz, colSz ); 12. newY = initArray ( rowSz, 1 ); 13. for j = 1 to size(ai, ‘rows’) // for each unique individual 14. start = ai[j,1]; 15. stop = ai[j,2]; 16. //copy the features of every image belonging to a particular individual 17. indvMat = trData [start…stop, 1…end]; 18. // check if this image is known to belong to any of the individuals in trData; 19. // if so, remove it so it will not be scored against itself. 20. if ( Xi ϵ trData[start…stop, 1…end] ) 21. indvMat = trData[start…stop, 1…end]; 22. delete(Xi, indvMat); 23. y = 1 // This is a matching pair. This does not apply to a test image 24. else 25. y = 0 // This is a non-matching pair. This does not apply to a test image 26. end if 27. col = 1; // To index through the regions in newData 28. for k = 1 to lastCol step numFtrs // for each region 29. // Compute distance measures 30. thisRegion1 = indvMat[1…end, k : k+numFtrs-1]; 31. thisRegion2 = Xi; 32. p = distance( thisRegion1, thisRegion2, distMethod ); 33. s = std(p); 34. if ( s >= 1 ) 35. newData[j, col] = s / mean(p); 36. else 37. newData[j, col] = s * mean(p); 38. end if 39. newY[j] = y; // This does not apply to a test image 40. col = col + 1; 41. end for 42. end for 43. Apair = newData; 44. Dpair = newY; 45. return (Apair, Dpair); images split into two albums, one for facial age estimation (album b) and the other for age-invariant face recognition (AIFR) (album a); album a is used in this work. FG-NET is a dataset of 1002 Caucasian face images and is suitable for both facial age estimation and AIFR. CACD is a dataset containing facial images of 163446 celebrities crawled from imdb.com. However, in this work, we only used images of African-Americans in the CACD dataset, this is done in order to validate the model across different ethnicities since FG-NET is purely Caucasian and FAGE is fairly small in size. We downloaded several lists of African-American actors/actresses on imdb.com, combined these lists and after removing duplicates, we found 877 names, but only 89 of them were present in the CACD dataset. CACD dataset contains a lot of noisy images and several images for an individual at the same age. Therefore, for each individual, we collected one image per age and ended up with 889 face images, we also collected all images of all 89 African-Americans found in CACD and found 7363 face images. Throughout this paper, the first subset of CACD is referred to as CACD-Unique-Africans, while the second is referred to as CACD-Africans.

It can be observed in table 1 that although CACD is a very large dataset compared to FG-NET and FAGE, the agegaps between individual images in both FAGE and FG-NET are higher than in CACD, although CACD has several images for each subject, the low individual age variation between faces images makes recognition easier on CACD than on FG-NET and FAGE.

Table 1. Datasets Statistics

SN	Metric	FAGE (Album a)	FG-NET	CACD (Unique-Africans)	CACD (Africans)
1	Total Number of images	212	1002	889	7363
2	Number of individuals	35	82	89	89
3	Number of individualized face pairs (#1 × #2)	7420	82164	79121	655307
4	Age range (years)	0 – 60	0 – 69	15 – 61	15 – 61
5	Average Age gap/individual (years)	14	45	10	10
6	Average number of images per individual	6	12	10	83
7	Ethnicity	African	Caucasian	African-American	African-American

• 4.2.    Experiments

  All experiments were carried out using MATLAB R2016a. Experiments on FAGE and FAGE were carried out on a Windows 10 laptop with Intel Core i5 processor and 4GB RAM while experiments on CACD were carried out on a Windows 10 desktop with Intel Core i5 processor and 16GB RAM. For training and testing, Support Vector Machines (SVM) was used with a Radial Basis Function (RBF) kernel which is basically a Gaussian kernel and alpha coefficients initialized to a vector of zeros. The classification cost was specified as a mirrored 2 × 2 identity matrix specifying a misclassification cost of 1 either for a false positive or a false negative.

• 4.3.    Proof of a Good Fit

Face preprocessing was done with the method in [35] and each face was divided into 10 face regions as described in [33]. From each face region, raw pixel and Local Binary Patterns (LBP) features were collected. The LBP features were collected both at each face region (referred to as LBP_FR) as well as from the whole face (referred to as LBP_WF), thus 3 feature types were extracted from each face. After features extraction, the individualized face pairing model was employed to pair matching and non-matching face embeddings. Note that the resulting quantity of face pairs increases with increasing dataset size as shown in Table 1. The resulting exhaustive list is balanced as described in definition 5 and the set of balanced datasets are used train an SVM model using k -fold cross-validation where k=n (the number of individuals in the respective dataset). More so, in each fold, n different models are trained and used for prediction so that the most frequently predicted class (negative or positive) for each pair is adopted as the final predicted class. Of course, this is computationally demanding, but it often guarantees high accuracies as seen from the results in Table 2. The basic idea is that all n classifiers cannot be wrong all the time and the most frequently predicted class (the modal predicted class) by this n classifiers, is very likely to be the correct class.

Table 2 shows the rank-1 recognition accuracies on the four datasets. As it can be observed from the table, recognition accuracies were generally best with LBP_FR achieving a 100% recognition on all datasets except FG-NET on which it achieved 97.01% accuracy. With regards to the datasets, it is very obvious that our face-pairing model found the two CACD subsets very trivial despite the large size of CACD-Africans subset, this is because of the low individual age gap between CACD images (10 years) and the availability of multiple images for each age. In fact, from our review of previous results on AIFR datasets, CACD is one of the datasets whose results quickly peaked due to the reason just explained. On the contrary, the small size and the large individual age gaps in FG-NET has made it very difficult to reach such high accuracies on FG-NET despite how old the dataset has been. A similar characteristic of FAGE has made its accuracy also lower than on CACD. From the results in Table 2, one can observe that the in addition to the individualized face pairing model, the method of taking the modal predicted class improved the prediction accuracy of the model and this is more impressive when we considered the fact that only a 1D vector of length 10 (from 10 face regions) is passed to the learning algorithm for each face pair.

Table 2. AIFR Recognition Accuracies

Feature type	Recognition accuracies (%)
	FAGE (Album a)	FG-NET	CACD (Unique-Africans)	CACD (Africans)
Raw pixel	93.40	87.92	100	100
LBP_WF	99.53	95.21	99.89	99.92
LBP_FR	100	97.01	100	100

Due to the high accuracies reported on all the datasets and for most feature types, it is natural for a reader of this paper to suspect overfitting. Therefore, in this subsection, we provide explanations to the high accuracy and to the fact that the model was not overfitting. From a Machine Learning standpoint, usual causes of overfitting include too many features, too little training data, and unregularized learning among others.

First, the learning algorithm was effectively regularized using the box constraint parameter of the SVM. The box constraint parameter maintains a mathematical relationship with the classification cost, the prior probabilities and the optimization weights to effectively regularize learning and prevent overfitting.

Secondly, as earlier stated, k -fold cross-validated learning was employed in all cases. k -fold cross-validation is regarded as one of the most robust and reliable validation protocols in Machine Learning, because it allows every single observation in a dataset to be used for testing once and for training k-1 times, making it possible to have a more generalized evaluation of the algorithm’s performance across the entire dataset. In fact, in contrast to 5-fold or 10-fold often used in k -fold cross-validation, our k=n (the number of individuals in a dataset) where k ranges from 35 to 89. Considering the huge number of face pairs produced by our face-pairing model (ranging from 7420 to 655307), such values of k are quite reasonable, yet computationally demanding.

Thirdly, in each fold of cross-validation, n different classifiers are trained and tested on n different sets of face pairs giving n different predictions on each face pair. This makes it possible to obtain for each face pair, the mode of predictions as the final prediction for that face pair. Considering the large value of n in the concerned datasets, this makes the overall cross-validated learning procedure more computationally intensive, but the result is near-perfect AIFR accuracies.

Finally, to be sure we are not overfitting on small datasets, we have experimented on a large subset of CACD containing 7363 face images of 89 African-American celebrities and giving rise to 655307 face pairs. This is perhaps one of the reasons why we could not use the entire CACD dataset for experiments as 163446 images of 2000 celebrities would give rise to 326, 892, 000 face pairs and this would be extremely computationally intensive. Thus, one could say that the individualized face-pairing model is mostly suited to small to moderately sized datasets. Agreeably, our model is still far less computationally intensive than an exhaustive face-to-face pairing model which could have resulted in 163446 × 163446 = 26, 714, 594, 916 face pairs.

• 4.4.    Comparative Analysis

  Comparison of our results with other results can only be possible on the FG-NET dataset, since not many works have yet used the FAGE dataset for AIFR and the same goes for the CACD subsets used here. However, in order to see the trend of AIFR performance on FG-NET vis-à-vis CACD, we have presented the previous accuracies on CACD as well. Table 3 presents a comparison of AIFR recognition accuracy rates on the FG-NET dataset over a 10-year period and on CACD over a 7-year period. It is obvious from the table that within 2 years after its release, accuracies on CACD have already surpassed that on FG-NET after over 2 decades of its release. This further testifies to the difficulty posed by the small size cum big age gaps in the FG-NET dataset. Also, in Table 3, it is obvious that our model outperforms most other works on CACD although a reader may quickly argue that we are not using the same CACD dataset, but the point is that most works used the validation set of CACD which contains 4000 carefully selected images (2000 matching pairs and 2000 non-matching pairs) for validation, whereas we have used over 7000 images from the raw/noisy CACD training set and have generated 655307 face pairs from that. So, ours is even more elaborate than what most other works have used and we have used only a 10-magnitude vector to learn and predict.

5.    Conclusion and Future Works

Also, from Table 3, only two works seem to outperform our model on FG-NET in terms of recognition accuracy. But on a closer look, TGF [36] used a subset of FG-NET – the adult images – which is significantly smaller in size than the entire FG-NET. Also, we observed that many works reported their True Positive (TP) rates which is often better than the accuracy rates and this could be what was reported in WLBP-UDP [18] . For instance, in our experiments, we obtained a TP rate of 100% on FG-NET with LBP_FR while accuracy was 97.01%. However, it is significant that our result still outperforms even most deep learning models on FG-NET.

Table 3. Comparison of age-invariant face recognition accuracies on FG-NET and CACD datasets

Method	Validation protocol	Accuracy (%) [FG-NET; CACD]
MFDA [16]	LOO	[47.5; -]
WLBP-UDP [18]	LOPO	[100; -] *
HFA [20]	LOPO	[69.0; -]
CARC [21]	10-fold CV	[-; 83.4]
TGF [36]	LOPO	[97.56; -] *
LF-CNN [27]	LOPO; 10-fold CV	[88.1; 98.5]
CANN [29]	LOPO; 10-fold CV	[86.5; 92.3]
Identity Inference [26]	LOPO	[88.23; -]
OE-CNN [37]	Mega Face challenge protocol; 10-fold CV	[58.21; 99.2]
Deep feature encoding [32]	LOPO	92.23%
DAL [38]	LOPO; 10-fold CV	[94.5; 99.4]
MTL-Face [39]	LOPO; 10-fold CV	[94.78; 99.55]
AIM [40]	LOPO; 10-fold CV	[93.20; 99.76]
IFP (Ours)	LOPO	[97.01; 100]

In this work, an individualized face-pairing model is presented for Age-Invariant Face Recognition (AIFR). The face-pairing model is inspired by the personalized nature of aging and thus employs it to build face-individual matching and non-matching pairs for AIFR training and validation. The developed face-pairing method is particularly suited (but not restricted) to small and moderately sized datasets because it creates a large ( m × n , m being the size of the dataset and n, the number of unique individuals in the dataset) set of face pairs for which a similarity score vector is obtained using hamming distance metric. The developed model was validated on 2 publicly available datasets (FG-NET and CACD) and 1 local dataset (FAGE). The results on all the datasets confirms the intuition of the model as it achieves near-perfect accuracy and also outperforms several state-of-the-art AIFR models.

Future directions will include validating the developed model on larger datasets on High Performance compute infrastructures because of the potential computational demand. Also, we shall explore different distance metrics such as Spearman’s rank correlation and cosine distance etc. There will also be the possibility of integrating the developed model within a deep architecture either for deep features extraction only or for complete learning (i.e., feature extraction and classification).