An Integrated Symmetric Key Cryptographic Method – Amalgamation of TTJSA Algorithm, Advanced Caesar Cipher Algorithm, Bit Rotation and Reversal Method: SJA Algorithm
Автор: Somdip Dey, Joyshree Nath, Asoke Nath
Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs
Статья в выпуске: 5 vol.4, 2012 года.
Бесплатный доступ
In this paper the authors present a new integrated symmetric-key cryptographic method, named SJA, which is the combination of advanced Caesar Cipher method, TTJSA method, Bit wise Rotation and Reversal method. The encryption method consists of three basic steps: 1) Encryption Technique using Advanced Caesar Cipher, 2) Encryption Technique using TTJSA Algorithm, and 3) Encryption Technique using Bit wise Rotation and Reversal. TTJSA Algorithm, used in this method, is again a combination of generalized modified Vernam Cipher method, MSA method and NJJSAA method. Nath et al. already developed some symmetric key encryption methods namely MSA, DJSA, DJJSA, modified DJJSA, NJJSA, TTJSA, TTSJA, DJMNA, UES-I, UES-II etc. The cryptanalysis shows that TTJSA is free from standard cryptographic attacks such as differential attack, plain text attack or any brute force attack. In the present method the authors have used advanced modified Caesar Cipher method where the authors have modified the standard Caesar Cipher method and then they applied TTJSA method to make the entire crypto system very hard to break. The present method has been tested on different plain text specially with repeated character and the spectral analysis of the plain text and the encrypted is also been shown. The spectral analysis shows that the present cryptography method, SJA can not be broken with any kind of standard cryptography attack. The authors propose that the present method will be most suitable for password, SMS or any kind of small message encryption.
Caesar Cipher, TTJSA, MSA, NJJSAA, UES, DJMNA, Cryptography
Короткий адрес: https://sciup.org/15010700
IDR: 15010700
Текст научной статьи An Integrated Symmetric Key Cryptographic Method – Amalgamation of TTJSA Algorithm, Advanced Caesar Cipher Algorithm, Bit Rotation and Reversal Method: SJA Algorithm
Published Online June 2012 in MECS DOI: 10.5815/ijmecs.2012.05.01
Due to tremendous growth in communication technology now the security of data is a really a big issue.
In banking system the data must be fully secured. Under no circumstances the authentic data should go to hacker. In defense the security of data is much more prominent. The leakage of data in defense system can be highly fatal and can cause too much destruction. Due to this security issue different cryptographic methods are used by different organizations and government institutions to protect their data online. But, cryptography hackers are always trying to break the cryptographic methods or retrieve keys by different means. For this reason cryptographers are always trying to produce different new cryptographic method to keep the data safe as far as possible.
The cryptographic methods can be divided into two types: (i) symmetric key cryptography, where the same key is used for encryption and for decryption purpose. (ii) Public key cryptography, where we use one key for encryption and one key for decryption purpose.
Symmetric key algorithms are well accepted in the modern communication network. The main advantage of symmetric key cryptography is that the key management is very simple. Only one key is used for both encryption as well as for decryption purpose. There are many methods of implementing symmetric key. In case of symmetric key method, the key should never be revealed /disclosed to the outside world or to other user and should be kept secure. The key should be known to sender and the receiver only and no one else.
The present algorithm i.e. SJA is also symmetric key cryptographic method, which is basically based on advanced modified Caesar Cipher method [1], TTJSA [2], which itself is based on generalized modified Vernam Cipher [2], MSA [3] and NJJSAA [4], and Bit Wise Rotation and Reversal Technique, which is developed from Bit Reversal technique [13] invented by Panduranga H. T. and Naveenkumar S. K. Depending on the key entered by the user the functions of generalized modified Caesar Cipher and TTJSA are called randomly and then executed, and at last Bit Wise Rotation and Reversal technique will be executed on the final step to make the encryption more strong. In the present paper we have also introduced multiple encryption as well as multiple decryption method.
-
II. Algorithm Used In The Present Work
In this method the authors apply a advanced form of Caesar Cipher [1] cryptographic method. In cryptography, a Caesar cipher, also known as a Caesar's cipher or the shift cipher or Caesar's code or Caesar shift, is one of the simplest and basic known encryption techniques. It is a type of replacement cipher in which each letter in the plaintext is replaced by a letter with a fixed position separated by a numerical value used as a "key". But, in this method, SJA, any character (ASCII value 0-255) are not separated by a fixed numerical value, in fact it is a variable numerical value, which is dependent on a nonlinear polynomial function.
This present method is achieved by executing following two methods in random:
-
(i) Encrypt the data using generalized modified Caesar Cipher method
-
(ii) Encrypt data using TTJSA method
-
(iii) Encrypt The data using Bit wise rotation
REVERSAL TECHNIQUE
In the present method, SJA, the user enters a secret key called as password and from that key we generate unique codes, which are successively used to encrypt the message. For decryption purpose we use just reverse process to get back the original plain text. During decryption the user has to enter the same secret key otherwise the decryption will not be successful. Now we will describe in detail the encryption procedure.
A. Encryption of data using modified Caesar Cipher:
-
1) Generation of Code and power_ex from the Secret Key
The key is provided by the user in a string format and let the string be ‘pwd[]’. From the given key we generate two numbers: ‘code’ and ‘power_ex’, which will be used for encrypting the message. First we generate the ‘code’ from the pass key.
Generation of code is as follows:
code = Mod(pseudo_code, 16).
If code=0, then we set code =pseudo_code
The Algorithm for this is as follows:
Let us assume, pwd[] = key inserted by user pp= 2i , i=0,1,2,……..n; n ∈ N.
Note: i can be treated as the position of each character of the key.
Step-1 : p[] = pwd[]
Step-2 : pp = 2i
Step-3 : i=0
Step-4 : p[i] = pwd[i];
Step-5 : p[i] = p[i] * strlen(pwd) * pp;
Step-6: csum = csum + p[i];
Step-7: i=i+1
Step-8: if i < length(pwd) then go to step-4
Step-9: if csum ≠ 0 then go to Step-10 otherwise go to Step-14
Step-10: c = Mod(csum , 10)
Step-11: pseudo_code=pseudo_code +c;
Step-12: csum = Int(csum / 10)
Step-13: Go to step-9
Step-14: code =Mod (pseudo_code, 16)
Step-15: End
Note: length(pwd)= number of characters of the secret key pwd[].
The ‘power_ex’ is calculated as follows:
We generate power_ex from the pseudo_code generated from the above method. We add all the digits of the pseudo_code and assign it as temporary_power_ex. Then we do modular operation on temporary_power_ex with code and save the resultant as power_ex. i.e. power_ex =Mod (temporary_power_ex, code)
If power_ex = 0 OR power_ex = 1, then we set power_ex = code.
For example, if we choose the password, i.e. the key to be ‘hello world’.
Then, length of pwd = 11
code = 10
power_ex = 4
Thus, we generate code and power_ex from the key provided by the user.
-
2) Encrypting the Message using code and power_ex
Now we use the code and power_ex, generated from the key, to encrypt the main text (message). We extract the ASCII value of each character of the text (message to be encrypted) and add the code with the ASCII value of each character. Then with the resultant value of each character we add the (power_ex)^i, where i is the position of each character in the string, starting from ‘0’ as the starting position and goes up to n, where n=position of end character of the message to be encrypted, and if position = 0, then (power_ex)^i = 0.
It can be given by the formula: text[i] = text[i] + code + (power_ex)i
If text[i] > 255 then text[i] = Mod(text[i],256) : ‘i’ is the position of each character in the text and text[] is the message to be encrypted, where text[i] denotes each character of the text[] at position ‘i’.
For example, if the text to be encrypted is ‘cccc’ and key=hello world, i.e. text[]=cccc and pwd=hello world, then c0 ->99+10+0 =109->m c1 ->99+10+4 =113->q c2 ->99+10+16=125->} c3 ->99+10+64=173->¡ where 0-3 are the positions of ‘c’ in text[](as per formula given above). The text ‘cccc’ becomes ‘mq}¡’ after execution of the above method.
Since, the value of (power_ex)i increases with the increasing number of character (byte) i.e. with the increasing number of string length, so we have applied the method of Modular Reduction [11][12] to reduce the large integral value to a smaller integral value.
To apply Modular Reduction we apply the following algorithm:
Step 1: n = power_ex * code * 10 ;generate a random number ‘n’ from code and power_ex
Step 2: calculate nth prime number
Step 3:i=0
Step 4: (power_ex)i = Mod( (power_ex)i ,( nth prime number))
Step 5: i=i+1
Step 6: if i Step-7: End Following the above step, we can reduce the value of (power_ex)i to a significantly smaller usable number. 3) Algorithm for Decryption (Advanced Caesar Cipher) For this step we basically reverse the process of encryption technique used in the modified Caesar Cipher. And use the following formula: text[i] = text[i] - code - (power_ex)i Note: If, ASCII value of text[i] < 0, then set text[i] =Mod (text[i], 256); ‘i’ is the position of each character in the text and text[] is the message to be encrypted, where text[i] denotes each character of the text[] at position ‘i’.
B. Encrypt the data using TTJSA: TTJSA method is a combination of 3 distinct cryptographic methods, namely, (i) Generalized Modified Vernam Cipher Method, (ii) MSA method and (iii) NJJSA method. To begin the method a user has to enter a text-key, which may be at most 16 characters in length. From the text-key the randomization number and the encryption number is calculated using a method proposed by Nath et al. A minor change in the text-key will change the randomization number and the encryption number quite a lot. The method have also been tested on various types of known text files and have been found that, even if there is repetition in the input file, the encrypted file contains no repetition of patterns. 1) Algorithm of TTJSA (Encryption) Step 1: Start Step 2: Initialize the matrix mat[16][16] with numbers 0 to 255 in row major wise. Step 3: call keygen() to calculate randomization number (=times), encryption number (=secure) Step 4: call randomization() function to randomize the contents of mat[16][16]. Step 5: times2=times Step 6: copy file f1 into file2 Step 7: k=1 Step 8: if k>secure go to Step 15 Step 9: p=k%6 Step 10: if p=0 then call vernamenc(file2,outf1) times=times2 call njjsaa(outf1,outf2) call msa_encryption(outf2,file1) else if p=1 then call vernamenc(file2,outf1) times=times2 call msa_encryption(outf1,file1) call file_rev(file1,outf1) call njjsaa(outf1,file2) call msa_encryption(file2,outf1) call vernamenc(outf1,file1)^ times=times2 else if p=2 then call msa_encryption(file2,outf1) call vernamenc(outf1,outf2)^ set times=times2 call njjsaa(outf2,file1) else if p=3 then call msa_encryption(file2,outf1) call njjsaa(outf1,outf2) call vernamenc(outf2,file1) times=times2 else if p=4 then call njjsaa(file2,outf1) call vernamenc(outf1,outf2) times=times2 call msa_encryption(outf2,file1) else if p=5 then call njjsaa(file2,outf1) call msa_encryption(outf1,outf2) call vernamenc(outf2,file1) times=times2 Step 11: call function file_rev(file1,outf1) Step 12: copy file outf1 into file2 Step 13: k=k+1 Step 14: goto Step 8 Step 15: End 2) Algorithm of vernamenc(f1,f2) Step 1: Start vernamenc() function Step 2: The matrix mat[16][16] is initialized with numbers 0-255 in row major wise order Step 3: call function randomization() to randomize the contents of mat[16][16]. Step 4: Copy the elements of random matrix mat[16][16] into key[256] (row major wise) Step 5: pass=1, times3=1, ch1=0 Step 6: Read a block from the input file f1 where number of characters in the block 256 characters Step 7: If block size < 256 then goto Step 15 Step 8: copy all the characters of the block into an array str[256] Step 9: call function encryption where str[] is passed as parameter along with the size of the current block Step 10: if pass=1 then times=(times+times3*11)%64 pass=pass+1 else if pass=2 then times=(times+times3*3)%64 pass=pass+1 else if pass=3 then times=(times+times3*7)%64 pass=pass+1 else if pass=4 then times=(times+times3*13)%64 pass=pass+1 else if pass=5 then times=(times+times3*times3)%64 pass=pass+1 else if pass=6 then times=(times+times3*times3*times3)%64 pass=1 Step 11: call function randomization() with current value of times Step 12: copy the elements of mat[16][16] into key[256] Step 13: read the next block Step 14: goto Step 7 Step 15: copy the last block (residual characters, if any) into str[] Step 16: call function encryption() using str[] and the no. of residual characters Step 17: Return 3) Algorithm of function encryption(str[],n) Step 1: Start encryption() function Step2: ch1=0 Step 3: calculate ch=(str[0]+key[0]+ch1)%256 Step 4: write ch into output file Step 5: ch1=ch Step 6: i=1 Step 7: if in then goto Step 13 Step 8: ch=(str[i]+key[i]+ch1)%256 Step 9: write ch into the output file Step 10: ch1=ch Step 11: i=i+1 Step 12: goto Step 7 Step 13: Return 4) Algorithm for Decryption Step 1: Start Step 2: initialize mat[16][16] with 0-255 in row major wise Step 3: call function keygen() to generate times and secure Step 4: call function randomization() Step 5: set times2=times Step 6: call file_rev(f1,outf1) Step 7: set k=secure Step 8: if k<1 go to Step 15 Step 9: call function file_rev(outf1,file2) Step 10: set p=k%6 Step 11: if p=0 then call msa_decryption(file2,outf1) call njjsaa(outf1,outf2)^ call vernamdec(outf2,file2)^ times=times2 else if p=1 then call function vernamdec(file2,outf1) set times=times2 call function msa_decryption(outf1,outf2) call fumction njjsaa(outf2,file2) call function file_rev(file2,outf2) call function msa_decryption(outf2,outf1) call function vernamdec(outf1,file2) times=times2 else if p=2 then call njjsaa(file2,outf1) call vernamdec(outf1,outf2) times=times2 call msa_decryption(outf2,file2) else if p=3 then call vernamdec(file2,outf1) times=times2 call njjsaa(outf1,outf2) call msa_decryption(outf2,file2) else if p=4 then call msa_decryption(file2,outf1) call vernamdec(outf1,outf2) times=times2 call njjsaa(outf2,file2) else if p=5 then call vernamdec(file2,outf1) times=times2 call msa_decryption(outf1,outf2) call njjsaa(outf2,file2) Step 12: copy the content of file2 to outf1 Step 13: set k=k-1 Step 14: Goto Step 8 Step 15: End 5) Algorithm of function vernamdec(f1,f2) The algorithm of vernamdec() function is same as vernamenc() function. Here the only difference is that decryption() function is called instead of encryption() function. 6) Algorithm of decryption(str[],n) Step 1: Start Step 2: ch1=0 Step 3: ch=(256+str[0]-key[0]-ch1)%256 Step 4: write ch into the output file Step 5: i=1 Step 6: if in then goto Step 12 Step 7: ch=(256+str[i]-key[i]-str[i-1]) %256 Step 8: write ch into the output file Step 9: i=i+1 Step 10: goto Step 6 Step 11: ch1=str[n-1] Step 12: Return 7) Algorithm of function file_rev(f1,f2) Step 1: Start Step 2: open the file f1 in input mode Step 3: open the file f2 in output mode Step 4: calculate n=sizeof(file f1) Step 5: move file pointer to n Step 6: read one byte Step 7: write the byte on f2 Step 8: n=n-1 Step 9: if n>=1 then goto step-6 Step 10: close file f1, f2 Step 11: Return 8) Njjsaa Algorithm Nath et al. [2] proposed a method which is basically a bit manipulation method to encrypt or to decrypt any file. The encryption number (=secure) and randomization number (=times) is calculated according to the method mentioned in MSA algorithm [1]. Step 1: Read 32 bytes at a time from the input file. Step 2: Convert 32 bytes into 256 bits and store in some 1- dimensional array. Step 3: Choose the first bit from the bit stream and also the corresponding number(n) from the key matrix. Interchange the 1st bit and the n-th bit of the bit stream. Step 4: Repeat step-3 for 2nd bit, 3rd bit...256-th bit of the bit stream Step 5: Perform right shift by one bit. Step 6: Perform bit(1) XOR bit(2), bit(3) XOR bit(4),...,bit(255) XOR bit(256) Step 7: Repeat Step 5 with 2 bit right, 3 bit right,...,n bit right shift followed by Step 6 after each completion of right bit shift. 9) Msa (Meheboob, Saima, Asoke) Encryption And Decryption Algorithm Nath et al. (1) proposed a symmetric key method where they have used a random key generator for generating the initial key and that key is used for encrypting the given source file. MSA method is basically a substitution method where we take 2 characters from any input file and then search the corresponding characters from the random key matrix and store the encrypted data in another file. MSA method provides us multiple encryptions and multiple decryptions. The key matrix (16x16) is formed from all characters (ASCII code 0 to 255) in a random order. The randomization of key matrix is done using the following function calls: Step-1: Function cycling() Step-2: Function upshift() Step-3: Function rightshift() Step-4:Function downshift() Step-5:Function leftshift() N.B: Cycling, upshift, downshift, leftshift, rightshift are matrix operations performed (applied) on the matrix, formed from the key. The detail description of the above methods are given in MSA [1] algorithm. The above randomization process we apply for n1 times and in each time we change the sequence of operations to make the system more random. Once the randomization is complete we write one complete block in the output key file.
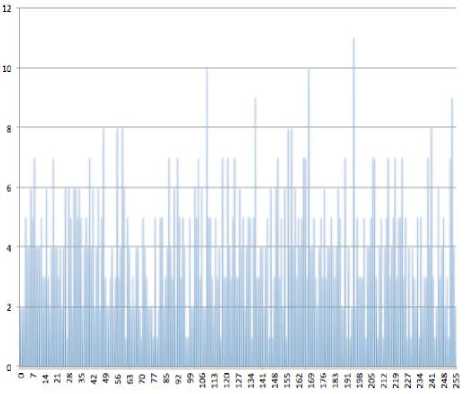
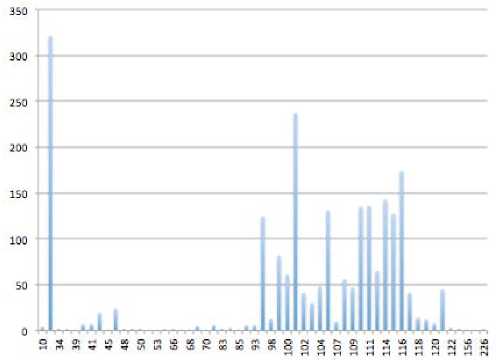
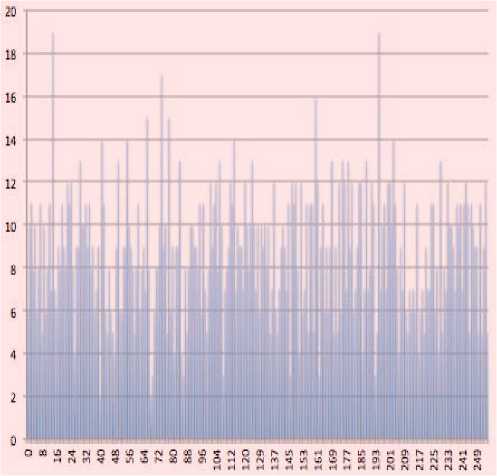
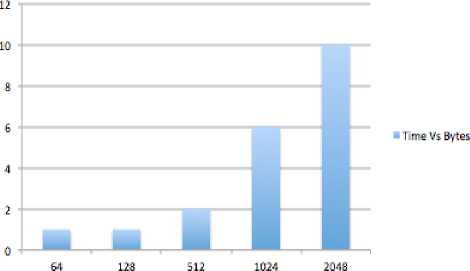
C. Encrypt the Data Using Bit Wise Rotation Reversal technique: In the Bit Reversal algorithm [13], proposed by Panduranga H. T. and Naveenkumar S. K., the pixel of the image, which is to be encrypted, is converted to its binary format and the number of bits, which is equivalent to the symmetric key (password) are reversed. In our method, SJA, we have applied the same concept but the only difference is that the method used in Bit Reversal is for encrypting Images, whereas we have modified the method, so that it can be used to encrypt any type of file. In this method, a password, which is given along with input file, is used to measure the effective length of the password and will be used in our modified bit rotation and reversal technique. Value of each byte of output file, which is encrypted using the previous techniques (Modified Caesar Cipher + TTJSA), is converted into equivalent eight bit binary format. Now length of password is considered for bit rotation and reversal. i.e., Number of bits to be rotated to left and reversed will be decided by the length of password. Let L be the length of the password and LR be the number of bits to be rotated to left and reversed (i.e. LR is the effective length of password). The relation between L and LR is represented by equation (1). LR =L mod 7 ------ eq. (1) where ‘7’ is the number of iterations required to reverse entire input byte. For example, CHin is the value of any random character (byte) of the output encrypted file. [B1 B2 B3 B5 B6 B7 B8] is equivalent eight bit binary representation of CHin. i.e. CHin -----> [B1 B2 B3 B5 B6 B7 B8] If LR=5, five bits of input byte are rotated left to generate resultant byte asiBuFTSftSjBjffjB'tP; I . After rotation, rotated five bits i.e.d'_ EvE?. В4ВЯ, get reversed as 5= Bq£> ? B^^'i and hence we get the resultant byte asI B^S-B^ S^is^S.; В2с'_ |. This resultant byte is converted to equivalent decimal number CHout i.e. I BhS?Bfl iPe;^'^.d'., B^-S, I -----> CHout where CHout is the value of output byte of resultant encryption. Since, the value of each character is dependant on the bit pattern, application of Bits Rotation & Reversal generates new value of each character and hence generates the encrypted file. Table 1 (a, b) show input and encrypted character respectively. For this encryption process given password is “1234” whose effective length (LR) = 4. Note: - If L=7, then LR=0. In this condition, the whole byte value of character gets reversed. Table 1 (a, b) [Password = 1234] a) Input Byte b) Output Byte ‘A’ (ASCII value = 65) (01000001) DC2 - Device Control 2 (ASCII value = 18) (00010010) ‘b’ (ASCII value = 98) (01100010) ‘&’ (ASCII value = 38) (00100110) III. Results And Discussions This method, SJA is used to encrypt different types of data and few results are given below: Message Encrypted Message ASCII character - 4 (1024 times) q«i± IAa}E%+ $&i^,- H v^S]EI±B,5xagI^ QyT*» 06 du°e 1 O<' "fl=4 °®wa 0 6uS^p-fi5Mn$ U-p--'uLSDE'U‘®^ fyl J 1 9_a\?EmUIOJ@°EdA o'-'IHa<*d+ ®N1»— %aN:T 3gFE|C£x). a*AU-°j°a66 %q—"— oC<6ZA_A9SXu^!Na 1 vwO> Om9,E(p bH(Ti2di$E - :U e'@"f& a-a»vl '}«uu~Ku№^2rnkU • %o~ eu@Axipd^,#fpJ M s>x^z $«,BiA ”#{ia l+ lA( e$ °V±3~® _ava'#f~c± >-3'aO§A1nD71D mf3'u J} EJi°AlJ1„-|bONr 0 ‘A a^Uu-VF oAf- =Gf,x, s-u@$±i0°E^2j{OscOA >QFUOi+®9 R ! f'h ;'%8T,qE/°r A] xA©E6SaA,lO0“~№3 • ]e<™W}?B °%| jY®Q|Aq:up}tIEAB> 0„'a)U'i Ep ”u„%$»'d UU0Xa1hiha@d- Л«,- -N%(eafo*T2Y G&W 5 -1 eUui7 9Q»anX3|Bp0|O /Y:$ F - • фАкА ‘ei O o...@e*‘D,Aj2+ %uha §A3°N?"e$+ AesE‘‘isFYu YYUYZiYAVI^ - -¥• uem 'HioU] L/ ‘•Of^xO/ZW k+ a;ZH h 0aLh © г 3io% h 0 °Ey@-Em|i%6¥s %“EOiQ2BXOEIeTLQi{N u?lW4ll )0 OKvhU'K UivxA «oaUUEIo%W1{ Yeiq)cE#^ • 6a0t Az> Bof?5J=®} ABCDABCDABCDA BCDABCDABCD ABCDABCDABCDA BCDABCDABCD (256 times ABCD; total 1024 bytes) y4'AdAt • eaEJ= dwtVS JUOU^-n ±0of Fig 1.1: Spectral Analysis of Frequency of Characters of 1024 ASCII Value(1) Q6Ta®i & a>TJ' 6"I^ zaN %okQw$h P ё¥ — Y^sYU$,°t ®m^ On t R- »1°2.;2.i- :+ H6TaOtA °9is^] ,hN№# u>¥QZ| zX1” Y| г iuAO^ j«“j "+ “А? Й AjYyX I o Ge°dP$ 1L 'Nad(hG| Fig 1.2: Spectral Analysis of Frequency of Characters of Encrypted data of 1024 ASCII value (1) HUs“u7 pd’&<%!- rYh | 9 j,a±9q| HD”¥hI-LT^+/| 1 Fw't 'e_AOuDoY+ _| K% h u~+ ° I - °6y,f-a %o£9ACU6d/ >,ieA@<T e @a#Yv' ,X^ |C=i%e£ u ?%> Gls (A'A a B h- sd1ZC“N n Ve)ae-e~suQ£ »Ou- As 2nd Test case we chose a random text file. The spectral analysis of the frequency of characters of the text file is shown in Fig 2.1 and Fig 2.2 shows the spectral analysis of frequency of characters of encrypted text. Szi uUU,cal-'A a| h “ggi ±i; IV. Spectral Analysis And Cryptanalysis Fig 2.1: Spectral Analysis of frequency of characters of an ordinary text file One of the classical cryptanalysis method used is by detecting the frequency of characters in the encrypted text (message). So to test the effectiveness of SJA method, spectral analysis of the frequency of characters are closely observed. Using this method, SJA, we ran many analysis and tested different strings as input and used various methods of cryptanalysis. To show the usefulness and integrity of this cryptographic module, we used spectral analysis of the frequency of characters. First, as a test case we chose, a file which contained 1024 ASCII value (1) and used this method to encrypt the data. Fig 1.1 shows the spectral analysis of frequency of characters of 1024 ASCII value (1) and Fig 1.2 shows the spectral analysis of frequency of characters of the encrypted data. Fig 2.2: Spectral Analysis of frequency of characters of the encrypted text file Thus from the above spectral analysis it is evident that the method, SJA, used here is very effective and there is no trace of any pattern in the encryption technique. Since this cryptographic technique uses multiple bit and byte level encryption, which again occurs multiple times, for this reason, the method used here is unique and almost unbreakable because there is no trace of any pattern. And this method is also effective against both Differential Cryptanalysis (Differential Attack) and Brute-Force Attack. V. Performance Analysis The performance of the SJA - Algoritm are tested extensively by taking different inputs. The following table shows the performance (on basis of time taken): INPUTS TIME TAKEN TO ENCRYPT TIME TAKEN TO DECRYPT 64 Bytes of any type of Message (Generally text containing Alpha-Numeric) 1 sec 1 sec 128 Bytes of any type of Message (Generally text containing Alpha-Numeric) 1 sec 1 sec 512 Bytes of any type of Message ( Generally text containing Alpha-Numeric) 2 secs 2 secs 1024 Bytes of any type of Message (Generally text containing Alpha-Numeric) 6 secs 6 secs 2048 Bytes of any type of Message (Generally text containing Alpha-Numeric) 10 secs 10 secs Thus from the above table we can see that as the number of bytes in a message increase, the time taken to encrypt or decrypt also increases. The following graph shows ‘the increase in time’ Vs ‘the increase in bytes of the message’: Time Vs Bytes Fig 3: Time Taken to Encrypt and Decrypt Vs Bytes in a Message From the above graph, it was found that time increses significantly with the increses in the number of bytes in the plain text file (with alphanumeric character). It is also evident that for maximum of 128 bytes per block of message (data), SJA - Algorithm works well and takes only 1 second time for encryption and decryption. For this reason, SJA – Algorithm can be used for network security also and is best used as 128 byte block cipher. Since, Modular Reduction is used in this SJA -Algorithm, the time taken for encryption and deryption also increases because Modular Reduction of large numbers needs massive computation. For this reason, SJA - algorithm can not be used for large files. But, this problem can be easily solved by integrating software and hardware acceleration to speed up the computation of Modular Reduction. VI. Conclusion and Future Scope In the present work we use three different algorithms to make the encryption process unbreakable from standard cryptographic attack. Our spectral analysis shows that our method is unbreakable We have applied our method on some known text where the same character repeats for a number of times and we have found that after encryption there is no repetition of pattern in the output file. We have tested this feature closely and have found satisfactory result in almost all cases. This has been possible as we have used modified Caesar Cipher method with polynomial function, modified Vernam Cipher method with feedback mechanism and also NJJSAA and MSA methods, where we use mainly the bit manipulation. We propose that this encryption method can be applied for data encryption and decryption in banks, defense, mobile networks, ATM networks, government sectors, etc. for sending confidential data. The above method, SJA, may be further strengthened using additional bit manipulation method. Acknowledgment Somdip Dey (SD) expresses his gratitude to all his fellow students and faculty members of the Computer Science Department of St. Xavier’s College [Autonomous], Kolkata, India, for their support and enthusiasm. AN is grateful to Dr. Fr. Felix Raj, Principal St. Xavier’s College, Kolkata for giving opportunity to work in the field of data hiding and retrieval.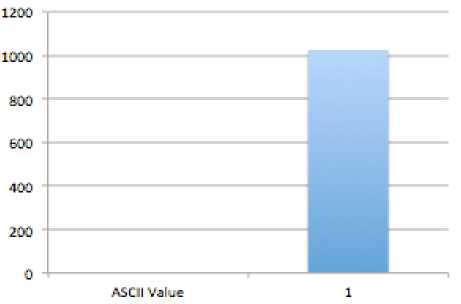
Список литературы An Integrated Symmetric Key Cryptographic Method – Amalgamation of TTJSA Algorithm, Advanced Caesar Cipher Algorithm, Bit Rotation and Reversal Method: SJA Algorithm
- http://www.purdue.edu/discoverypark/gk12 / downloads/Cryptography.pdf
- Symmetric key cryptosystem using combined cryptographic algorithms - Generalized modified Vernam Cipher method, MSA method and NJJSAA method: TTJSA algorithm " Proceedings of Information and Communication Technologies (WICT), 2011 " held at Mumbai, 11th – 14th Dec, 2011, Pages:1175-1180
- Symmetric Key Cryptography using Random Key generator: Asoke Nath, Saima Ghosh, Meheboob Alam Mallik: "Proceedings of International conference on security and management(SAM'10" held at Las Vegas, USA Jull 12-15, 2010), P-Vol-2, 239-244(2010).
- New Symmetric key Cryptographic algorithm using combined bit manipulation and MSA encryption algorithm: NJJSAA symmetric key algorithm: Neeraj Khanna,Joel James,Joyshree Nath, Sayantan Chakraborty, Amlan Chakrabarti and Asoke Nath : Proceedings of IEEE CSNT-2011 held at SMVDU(Jammu) 03-06 June 2011, Page 125-130.
- Advanced Symmetric key Cryptography using extended MSA method: DJSSA symmetric key algorithm: Dripto Chatterjee, Joyshree Nath, Soumitra Mondal, Suvadeep Dasgupta and Asoke Nath, Jounal of Computing, Vol3, issue-2, Page 66-71,Feb(2011)
- A new Symmetric key Cryptography Algorithm using extended MSA method :DJSA symmetric key algorithm, Dripto Chatterjee, Joyshree Nath, Suvadeep Dasgupta and Asoke Nath : Proceedings of IEEE CSNT-2011 held at SMVDU(Jammu) 3-5 June,2011, Page-89-94(2011).
- Symmetric key Cryptography using modified DJSSA symmetric key algorithm, Dripto Chatterjee, Joyshree Nath, Sankar Das, Shalabh Agarwal and Asoke Nath, Proceedings of International conference Worldcomp 2011 held at LasVegas 18-21 July 2011, Page-306-311, Vol-1(2011).
- An Integrated symmetric key cryptography algorithm using generalized vernam cipher method and DJSA method: DJMNA symmetric key algorithm : Debanjan Das, Joyshree Nath, Megholova Mukherjee, Neha Chaudhury and Asoke Nath: Proceedings of IEEE International conference : World Congress WICT-2011 to be held at Mumbai University 11-14 Dec, 2011, Page No.1203-1208(2011). .
- Symmetric key Cryptography using two-way updated – Generalized Vernam Cipher method: TTSJA algorithm, Trisha Chatterjee, Tamodeep Das, Shayan dey, Joyshree Nath, Asoke Nath , International Journal of Computer Applications(IJCA, USA), Vol 42, No.1, March, Pg: 34 -39( 2012).
- Ultra Encryption Standard(UES) Version-I: Symmetric Key Cryptosystem using generalized modified Vernam Cipher method, Permutation method and Columnar Transposition method, Satyaki Roy, Navajit Maitra, Joyshree Nath,Shalabh Agarwal and Asoke Nath, Proceedings of IEEE sponsored National Conference on Recent Advances in Communication, Control and Computing Technology-RACCCT 2012, 29-30 March held at Surat, Page 81-88(2012).
- Peter Montgomery, "Modular Multiplication Without Trial Division," Math. Computation, Vol. 44, pp. 519–521, 1985.
- W. Hasenplaugh, G. Gaubatz, and V. Gopal, "Fast Integer Reduction," 18th IEEE Symposium on Computer Arithmetic (ARITH '07), pp. 225– 229, 2007.
- Panduranga H T, Naveenkumar S K, "An image encryption approach using bit-reversal method ", NCIMP 2010, pp.181-183.


