An Introduction of Two and Three Dimensional Imprecise Numbers
Автор: Sahalad Borgoyary
Журнал: International Journal of Information Engineering and Electronic Business(IJIEEB) @ijieeb
Статья в выпуске: 5 vol.7, 2015 года.
Бесплатный доступ
Discuss the real line fuzzy concept into multi- dimensional based on the reference function so as to get new imprecise numbers called the two-dimensional and three-dimensional imprecise numbers and their complements. Two and three dimensional imprecise numbers are obtained in the form of Cartesian product of fuzzy numbers. To study their character some necessary definitions like partial presence, construction of membership function, membership value ,Indicator function etc. of two and three-dimensional imprecise numbers are defined with own notation. As per as possible, try to show all the properties of classical set theory that can be hold good in the present imprecise numbers with some examples. Set Operations are defined by maximum and minimum operators just like defined in the real line imprecise numbers. Further bring out a few graphical examples to verify the intersection and union of two and three dimensional imprecise numbers are the empty and the universal set respectively. Basically Intersection and union are the operators to obtain their properties.
Reference function, imprecise number, membership function, membership value, Indicator function, normal imprecise number, two-dimensional imprecise number, three-dimensional imprecise number
Короткий адрес: https://sciup.org/15013367
IDR: 15013367
Текст научной статьи An Introduction of Two and Three Dimensional Imprecise Numbers
Published Online September 2015 in MECS DOI: 10.5815/ijieeb.2015.05.05
Dimension study plays a vital role in the field of mathematics. Since the real life problems are not only in the single real line part. To get a complete solution of any physical problem we need solution of whole the dimension. For one face study of any experiment, two-dimension takes a part to know how much membership in this face and for the study of surface and volume three-dimension takes a part to know how much membership as a whole body in the surface and volume. So to study how much percentage is occupying as a member, called membership function along the respective axes, this article is come out.
In the article of Zadeh [1] some of the classical set properties are not satisfied, so Baruah has defined new complement definition of fuzzy set in the imprecise form that can be satisfied all the properties of classical set theory in their article [3].
Fuzzy numbers are defined in the Cartesian product form in the article [6], [7], [8], [9],[15]. All the Cartesian product fuzzy numbers are the order pair just like different dimensional co-ordinate points.
Imprecise numbers are the interval definable of fuzziness numbers which is explained in the preliminary section. Here, the concept of imprecise number over the real line defined in the Baruah[3],[4],[5],[8] is extended into particular form namely two and three dimensional imprecise numbers so that we can study effect of fuzziness as a membership in each and every part of the occupied body. Identification of effect of fuzziness character in the specific dimension will help to solve many difficult practical problems. For examples how must be attractive a drop of red light in the groups of decoration of color light is one of the important application of signal apply in different purpose by the various institutions. As red light has the longest wave length, among the same different colors having same weightiest, red light will certainly focus in eye in comparison to remaining color lights. In those places how much that signal solve their purposes are two and three dimensional imprecise numbers. Along with complement of membership function of two and three dimensional imprecise numbers defined with reference function help us to know much is the dullness of color can be present from the containing group of color lights.
Set is defined for all well-defined objects. So any two and three dimensional imprecise numbers nothing but are also sets that can satisfies all the properties of classical set theory. The set theory properties occur under the set operations of intersection and union are proof in the definition of two and three dimensional imprecise numbers with counter examples.
Rest of this article is organized as follows-Section II preliminaries, Section III introduction definition of two dimensional imprecise numbers and its complement along with prove of their properties, Section IV introduction definition of three dimensional imprecise numbers and their complement. Finally section V goes to the conclusion and the discussion.
-
II. Preliminaries
Before start of this article it is necessary to recall the definition of imprecise number, partial presence, membership value etc. over the real line which are discussed in the article of Baruah [3],[4],[5],[8]. Dhar [11],[12],[13],[14] and Borgoyary [14] are also defined same definitions in their articles to apply in some field of mathematics.
-
A. Imprecise Number
Imprecise number is a closed interval IV = [ a, P, y] is divided into closed sub-intervals with the partial presence of element P in both the intervals.
-
B. Partial Presence
Partial presence of an element in an imprecise real number [ a , P, y] is described by the present level indicator function p(x) which is counted from the reference function r(x) such that present level indicator for any x, a < x < y , is (pOO — r(x)) , where 0 < т (x) < p(x) < 1.
-
C. Membership Value
If an imprecise number N = [a,P,y] is associated with a presence level indicator function pv(x), where
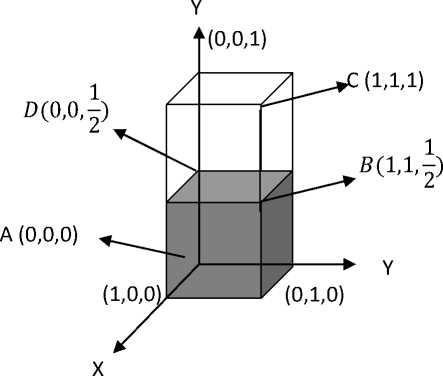
U ( 00, Un 00 = [ (• (00, 0, when a < x < P whenP < x With a constant reference function 0 in the entire real line. Where p(to is continuous and non-decreasing in the interval [ , ] , and ( ) is a continuous and nonincreasing in the interval [ , ] with pi (a)=p 2(y) = 0, (2) Then, ([((/?) — [((/?)) is called membership value of the indicator function ( ) D. Normal Imprecise Number A normal imprecise number N = [a, P, y] is associated with a presence level indicator function ( ), where ( ), Un00 = ] [(to, 0, when a < x < P h < < о therw ise With a constant reference function 0 in the entire real line. Where ( ) is continuous and non-decreasing in the interval [ , ] and ( ) is a continuous and nonincreasing in the interval [ , ] with ц ((a) = [ ((y) = 0 Я ((Р)=ц ((P ) = 1 (3) Here, the imprecise number would be characterized by {x, pv(x), 0 : x R R}, R being the real line. For any real line, 0 < p((x) < p((x) < 1 normal and subnormal imprecise number will be characterized in common, {x,n(to,P(to: x E R}, where [(x) is called membership function measured from the reference function ( ) and ( ( ) — ( )) is called the membership value of the indicator function. Here, the number is normal imprecise number when membership value of indicator function ц v(x) is equal to 1 otherwise subnormal if not equal to 1. Moreover it can be said that the universal set if the membership value of pN (%) equal to 1 and null or empty set if equal to 0. E. Complement For a normal imprecise number N= {x , pv(x), 0 : x E R} as defined above, the complement Nc = {x, 1,pv(x): xRR will have constant presence level indicator function equal to 1, the reference function being pv(x) for —m < x < TO. III. Two Dimensional Imprecise Number In the definition of Baruah [3], [4], [5] imprecise number is defined over the real line. It is along the X-axis. This case is studied if the effect of fuzziness over the physical significance is along the x-axis or the real line when all other remaining axes are already fully membership or the membership value having one. In practical such standard problems are limited. So, to study more practical problems it may be introduced two dimensional imprecise numbers. Two dimensional numbers are expressible in XY-plane. Here, imprecise number is defined in the two-dimensional form such a way that full membership along the x-axis and the y-axis are considered membership value as one and the other axes are already fully membership. For example at any instant one short of travelling of water wave up to what distance is the x-axis and the height of the tide occur during their rise is the y-axis. A. Definition A two dimensional imprecise number is a closed interval NXy = [(«X, ay), (Px, Py), (yx, yy)] which can be divided into sub intervals with a partial element is presence in both the intervals. Where all the points in this interval are element of Cartesian product of two sets X x Y and both the sets X and Y are the imprecise numbers. B. Definition Partial presence of an element in two-dimensional imprecise number Nxy = [( «x, ay), (Px, Py), (Ух, Уу )] is described by the present level indicator function p(x, y) which is counted from the reference function ( , ) such that present level indicator for any( , ), (ax,ay) < (x,y) < (Ух,Уу) i s (p(x,y) — r(x,y)) , where (0,0) < (^,у) < p(x, у) < (1,1). C. Definition For a two-dimensional imprecise number, NxY = [(«х. «у), (Ух, Уу), (Ух, Уу)], the indicator function will be represented and defined by М-NxY ( PxY 1 (Х,У), ) HXY2 (Х,У), I 0, ( «х, «у) < (x,y)< (Ух,Уу) (Ух,Уу) < (Х,У)< (Ух,Уу) о t he(wise Such that И XV1 («х,«у) = РхУ2(Ух,Уу) = 0 andPxy1(Ух,Уу) * 0,/^XY2 (Ух, Уу) * 0 where pXY 1(x,у) is non-decreasing function over the closed interval [(«х, «у), (Ух,Уу)] and fiXY2(x,y) is nonincreasing over the closed interval, [( , ), ( , )]. D. Definition For a two-dimensional normal imprecise number NXY = [(«х,«y),(Ух, Уу),(Ух,Уу)], the indicator function will be represented and defined by pN XY ( PxY1 (x,y), ) HXY2 (x,y), 0, ( «х,«у) < (x,y)< (Ух,Уу) (Ух,Уу) < (x,y)< (Ух,Уу) ot he(wise Such that И XV1 («х,«у) = ^2(Ух,Уу) = 0 and HXY 1(Ух,Уу) = HXY2(P х,У у) = 1 Where pXYY (x, у) is non-decreasing function over the closed interval [(«х, «у), (Ух,Уу)] and /iXY2(x,y) is nonincreasing over the closed interval, [(Ух, Уу ), (ух, Уу)]. E. Definition If a two-dimensional imprecise number NXY = [(«х, «у), (рх, Уу), (Ух, Уу)], is associated with a presence level indicator function Hnxy (x,y), Where ( PXY1 (x,y), ) HXY2(x,y), 0, ( «х,«у) < (x,y) < (Ух,Уу) (Ух, Уу) < (x,y) < (Ух,Уу) о t he(w ise With a constant reference function (0,0) in the entire the section X x Y. Here pXYY (x, у) is continuous and non-decreasing in the interval [(«х, «у), (Ух,Уу)] and ( , ) is a continuous and non-increasing in the interval [(Ух,Уу), (Ух,Уу)] with PXY1(«х,«у) = ^2(Ух,Уу) = 0 and Hxy 1(Ух,Уу) * 0,^2(Ух,Уу) * 0, Then, ( ^1(Ух,Уу) ) = (У, -У ^)х(у' -у ") (-^2(Ух,Уу)7 (Ух Ух) (Уу Уу) is called membership value of the indicator function ^VXY(x,y), where ЯtY1(Ух,Уy)=(У'х,У'y) ^XY2(Ух.Уy) = (y•,.y•y) F. Definition For a normal imprecise number ^XY = {(x, у), PVXY (x, у), (0,0): (x, у) E X x У) as defined above, the complement NXyC = {(x,У), (1,1),ДvхY(x,у): (x,у) E R x R (8) will have constant presence level indicator function equal to 1, the reference function being ^VXY(x,у) for -m < (x,у) < m Two dimensional imprecise numbers would be characterized by, {(x,у),ДхY 1(Х,У),^XY2(Х,У): (x,у) E X x Y ) where ( , ) and ( , ) are called membership function and the reference function of the indicator function defined above and the membership function is measured from the reference function, then tix^ (x1-x2)x(y1-y)2 (9) is called the membership value of the indicator function. Where, HXY1 (X,y) = (X !,yj and ^У2(Х,У) = (Х2,У2) respectively. The collection of all such elements is called to form a two dimensional imprecise set. If the membership value is equal to 1, then the imprecise set is called the three dimensional normal imprecise number. If the membership value is less than 1, the imprecise number is called the three dimensional subnormal imprecise number. Further if the membership value becomes 1 then a three dimensional universal imprecise set and null or empty set when the membership value becomes 0. Based on the conditions of classical set theory properties can be proposed into two dimensional imprecise numbers also. Intersection and union of two dimensional imprecise numbers X Fig. 1. Two dimensional imprecise number Here, membership function is A (Guxy(x,y)) — {(x,y),(|,|*,(0,0)} with the membership value 1 1 111 (2-0)х(2-0И2Х2) — 4 If A (M-XY 1,^XY2) — {(x,y),l-ixY 1 (х , y), HXY2(X, у): (x,y) ЕХхУ} And and the portions of the membership set of complement part can be obtained as A(ixYC(x,y)) xre {(x,y), (1,1), (o,1*) В (Ц XY 3 ,^XY4) — [(x,y),iHxY3(x,y),iUxY4(x,y): (x,y) Е Х х У), and Then, {Cx.y).(l,1),C|.0)}. Intersection: A(M-XY 1,fcY2)n В QxxY3> XxYt) _ f (x,y),min(/txY1(x,y),^xY3(x,y)), 1 (maxGaxY2(x,y), G“xy4 (x, y)), (x,y) Е Х х УJ Union: Now by the intersection and union definition of imprecise number, we have- Intersection: Portions of A((^(x.y)) П ЛGuxYC(x,y)) are —{ A (^XY1, ^XY2) U ( (XxY3, ^XY4) (x,y),m xx^XxY 1(x,y),JUxY3(x,y)), min(nxY2(x,y), G«xY4(x,y)), (x,y) Е Х х У } !(x, y), (min (2,1), min (2,1)) ,) (max(0,0),max(0,-** j — {(x,y),(2,2),(0,2)} Since all the imprecise numbers along the real line can be satisfied the theory of classical set and Boolean algebra. First it can be claimed that the theory of intersection and union of two dimensional imprecise numbers are empty and the universal set respectively. For this purpose let us consider a dram filled with half portion water along the X-axis and Y-axis respectively is shown in the following figure: with the membership value 1 11 (2-0)Х(2-2) — 0 to form an empty set. And Ly)/™^^^'""^). ( \ m»(l 1) / \ max(0,0) /] -M^D-GM) with membership value (1 1 1 \ G-^-0?0 to form an empty set. Since, union of two empty sets is again empty set. So, intersection of membership and complement of membership function of two dimensional imprecise numbers is a null or empty set to satisfy one of the classical set properties. Union: (A(lUxy(x,y))UA^x/fcy)) ((x,y), (max (2,1), max (-, 1)),) (min(0,0),min(0,|))j !(x,y), (max(1,1) ,mаx(-,-)),) (min(0,|),min(0,0))} = {(x,y), (1,1), (0,0)} и {(x,y), (1,1), (0,0)} _ ((x, y), (max(1,1), max (1, -)),) I (min(0,0), min(0,0))) = {(x,y), (1,1), (0,0)}, which gives membership value, (1 - 0) x (1 - 0) = 1 to form a two dimensional imprecise universal set. Thus by help of this graphical example it can be introduced property of two dimensional imprecise numbers as, A. Property- and (ii) ((-xy (x, y)) U A (-xyc(x,y)) = П, where 0 and Л are null and universal respectively. B. Property- Commutative laws Let Afey^y)) = {(x,y),^xyi(x,y),^xy2(x,y): (x,y) e X x y} and S(G«xy(x,y)) = {(x,y),^xy3(x,y),^xy4(x,y): (x,y) e X x У} be two dimensional imprecise numbers. Then (i) A(Guxy(x,y)) UB(Guxy(x,y)) = 5((Bxy(x,y)) uA((Bxy(x,y)) (ii) A(Guxy(x,y)) nB((uxy(x,y)) = Stoxy^y)) nA^xy^y)) Proof- If A((„„i(x.y))= 0,0 and BtftefcX» = {(},}),(;,;)) be two dimensional imprecise numbers, then A((Bxyi(x,y)) u B((Bxy2(x,y)) = f(max(l,l),max(2,l)),_ [(min(4,6),min(4,6)) ={(I,D,(6,6)} And S((Bxy2(x,y)) uA((Bxyi(x,y)) = max(|,|)A (\mm^/ Vin(6,4)/J ={(I,D,(6,6)} Hence proved (i) Proof- If AK-wx^ 0,(41)) andB((-xy2(x.y)) = {g.;)).(),))) be two dimensional imprecise numbers, then Afeyi^y)) П B((-xy2(x,y)) (min(|,|),min(|,|)), . (та^И^тЩ,^) ={(I,D,(4,4)} And B((—xy2 (x, y)) n A((—xyi(x, y)) = (f min(3'DA /Мб-М ^max^/j <1ИЧ)} Hence proved (ii) C. Property- Distributive Laws If A((^xyi(^y)), В((Мху2(х-У)) and С((^Ху3(х-у)) be three two dimensional imprecise number, then B((BxY2(X-y)) (i) A1^-'--y ' '.c (,.._.■.. ^ = А((ЙХУ1(Х-У))n B((^xY2(X-y)) u A((^xYi(x-y)) n C((BXY3(X-y)) I I ( B((BXY2(X-y)) \ (ii) A((feYi(X-y))u(nc№xY3(X-y))) = A^XYlC^y))u B№xY2(X-y)) nA((^xY1(X-y))U C((BXY3(X-y)) Let us prove the property (i) and (ii) with example, If A((BxYi(x-y))= {g-2)-(i-i)}, B(. ■ y). ;:' ', :1;,: and «(^^Иб-Э-б-Э}, then (B((BXY2(X-y))U\ A((BxY1(X-y))n( C(GUxY3(X-y)) * O4> \ ((тах(И)-тах(И))-р |(min(|-|)-min(|-|))P ={(l-D-(4-4)}n{(l-D-(l-l)} = f(min(l-l)-min(l-l))- _ |РтаЧ-!)-тЧЧ)) ={(l-D-(l-4)} and A((^xyi(x,y)) n B((^xY2(^-y)) U A((^xri(^-y)) n ССО^з^-У)) =T(min(i-3)-min(i-3))- _ Ртах(И)-тах(4-|)) и f(min(|-6)-min(|-6))-. |РтаЧ-!)-тЧЧ)) ={(l-l)-(4-4)}u{(6-6)-(l-!)} =|(max(l-6)-max(3-6))-_ [(min(4-4)-min(4-4)) ={(l-D-(4-4)} Hence proved (i) A«^xYi(«.y))u(B((t2(::y))) =oo и ^(m^n(ll),mln(ll)). ■ [(™“i(5'7)’™“x(54)) ={(l-2)-(44)}u{(64).(5.|)l = |(max(2'6)'max(2’6))’. |(„i„(l,l),mi„(l.l)) -{(24)-(l-l)} And A((ДXУ1(X,У)) u B((^xY2(^-y)) n A((ДxУ1(x,y)) u C((дxyз(x,y)) = f(max(l-l)-max(2-l))-_ |(т^п(4-|)-т^п(4-|))^ n f(max(l-6)-max(l-6))-_ [(mm^-lyrnm-^) = {(4)-(l-l)}n{(|-|)-(7-7)} = f(min(l-l)-min(l-l))- _ Ртах(|-|)-тах(|-|)) ={(l-D-(5-l)} Hence proved (ii) Further it can be verified that the following properties of classical sets are satisfied by the two-dimensional imprecise sets A(^XY(z-y)) , B(^XY(z-y)) and C(Axy(^y)): D. Idempotent Laws- E. Associatively Laws- -■ A(.,-x,,)u(u;;^>,j = (A(MxY(x,y)) U В(mxy(x,y))) U C(Mx,(x,y))) A.™.*^-;))) = (A(MxY(x,y)) n S(MxY(x,y)))c(^xY(x,y))) F. De Morgan’s Law- = A(Mx,C(x,y)) n В (mxyC(x,y)) (ii) (A(mxy(x, y)) П В(mxy(x, y))) = A(mxyC(x,y)) U В (mxyC(x,y)) IV. Three Dimensional Imprecise Number It is mentioned in the definition of two dimensional imprecise numbers that the effecting parts of a body of fuzziness are along the two axes and all others are already fully membership. Roughly any physical problem can be expressed more or less in the three dimensions form. So to study effect of fuzziness in the body along the length, breadth and height it may be introduces three dimensional imprecise numbers. Three dimensional numbers are expressible in XYZ-solid geometry. Here, imprecise number is defined in the three-dimensional form such a way that full membership along the x-axis, the y-axis and the z-axis respectively is considered membership value one. For example at any instant one short of travelling of solitary wave up to what distance is the x-axis and the height of the tide occur during their rise is the y-axis and thickness is the z-axis. A. Definition A three dimensional imprecise number is a closed interval Nxyz = [(«х,«у«г), (Pх,Py,Py),(Ух,Уy,Уz)] divided into sub intervals with a partial element is presence in both the intervals. Where all the points in this interval are element of Cartesian product of two sets X x Y x Z and the sets X, Y and Z are imprecise numbers. B. Definition Partial presence of an element in a three-dimensional imprecise real number Nxyz = [(«х, «у, «z),(Pх,Py,Pz),(Ух,Уy,Уz)] is described by the present level indicator function p (x, y, z) ,which is counted from the reference function r(x, y, z) such that present level indicator for any (x,y,z) , («х, «у, «z) < (x,y, z) < (Ух,Уу,Уг) is (p(x,y,z) -r(x,y, z)) , where (0,0,0) < r(x,y,z) < P(x,y,z) < (1,1,1). C. Definition For a three-dimensional imprecise number, NXyz = [(«х, «у«z), (Pх,Py,Py), (Ух,Уу,Уг)], the indicator function will be represented and defined by BnXyz ( Bxyz 1 (x-y-z)- = ) MxYZ2(x,y,z), I 0 Such that Mxyzi («z, «у, «z) = MxYZ2(yУ,Уy,Уz) = (0,0,0) and BXYZ1 (Рх, Ру, Pz) ^ 0, BxYZ2(Px, Ру, Pz') ^ 0 (13) where ( , , ) is non-decreasing function over the closed interval [( , ,«z ),(Pz, Ру, Pz)] and M-XYZ2 (x, y, z) is non-increasing over the closed interval, [( , , ),( , , )]. D. Definition For a three-dimensional normal imprecise number, Nxyz = [(«У,«y«z),(PУ,Py,Py),(УУ,Уy,Уz)], the indicator function will be represented and defined by ( Bxyz 1 (x.y, z), ) MxYZ2 (x,y,z), 0 Bnxyz = ( «х,«у,«г1 < (x,y,z) < (Pх,Py,Pz) (p:C,Py,Pz1< (x,y,z) < (Ух.Уу.Уя) otherw ise Such that BXYZI («х,«у,«г) = MxYZ2(УУ,Уy,Уz) = (0,0,0) and P-XYZ1 (P X, P у, PZ1 = BxYZ2 (P X, P у, PZ1 = 1 (14) where ( , , ) is non-decreasing function over the closed interval [( , ,«z ),(Px, Py, Pz)] and HXYZ2 (x, У,z) is non-increasing over the closed interval, [(Px,Py,Pz),(Yx,Yy,YzT]. E. Definition If a three-dimensional imprecise number, Nxyz = [(«x,«y«z),(Px,Py,Py'),(Yx,Yy,YzУ], is associated with a presence level indicator function ^NXY(X,y,Z), Where, ( ^XYZl(X,y,z), ) ^XYZ2(X,y,z), I 0 Bnxyz = ( ax,ay,az)< (x,y,z) < (Px,Py,Pz) With a constant reference function (0,0,0) in the coordinate section (Xx/xZ) . Here mxyzi(x, y, z) is continuous and non-decreasing in the interval [(«x, «y, «z), (Px,Py,Pz)] ] and Mxyz2(x, У, z) is a continuous and non-increasing in the interval with, [(Px,Py,Pz), (Yx, Yy, Yz)], such that HXYZ1 («х, «у, «z) = HxYZ2(Yx,Yy,Yz) = (0,0,0) and HXYZ1 (Px,Py,Pz) * 0,HxYZ2(Px,Py,Pz) * 0 Then (MXYZl(Px,Py,Pz) - ^XYZ2(Px,Py,Pz)) = (P'x-P"x)x(P'y — Py)x(P'z - P\) (15) is called membership value of the indicator function, ^nXYz (x, y, z), where Hxyzl (Px,Py,Pz) = (P' x, P' y,P'z) and HXYZ2 (Px,Py,Pz) = (P"x,P"y,P"z') F. Definition For a three-dimensional normal imprecise number Nxyz = {(x,y,z), ^NYxz(x,y,z), (0,0,z): (x,y,z) e X x Y x Z} as defined above, the complement NxyzC = {(x,y,z'),(1,1,1'),^NxYz(x,y,z'): (x,y,z) e X x Y x Z} will have constant presence level indicator function equal to 1, the reference function being ^NXY(x,y,z') for -TO < (x,y,z) < TO Three dimensional imprecise number would be characterized by, {(x,y,z),^xYzi(x,y,z'),^xYz2(x,y,z'): (x,y,z) eXx YxZ}, where ^l(x,y, z) and ^2(x,y, z) are called membership function and the reference function of the indicator function yNxy defined above and the membership function is measured from the reference function, then (^XYzl (x, У, z) — ^XYz2 (x, y,z)) = (xi - x2) x (yi - У2) x (zi - z2) (17) is called the membership value of the indicator function, Where ^XYZl(x,y,z) = (x^y^zi) and ^^YZ2(x,y, z) = (x2,y2,z2) respectively. The collection of all such elements is called to form a set is called three dimensional imprecise set. If the membership value is equal to 1, then the imprecise set is called the three dimensional normal imprecise number. If the membership value is less than 1, the imprecise number is called the three dimensional subnormal imprecise number. Further if the membership value becomes 1 the three dimensional universal imprecise set and null or empty set when the membership value becomes 0. Intersection and union of three dimensional imprecise numbers If A(HxYZl,^XYZ2>) = {(x,y,z),^xYzi(x,y,z),^xYZ2(x,y,z): (x,y,z) e X x Y x Z} And B(^XYZ3,^XYZ4) = {(x,y,z),^xYZ3(x,y,z),^xYZ4(x,y,z):(_x,y,z') eXxYxZ}, then Intersection: =1 (x, y, z), min(^xYzi (x, У, z), ^xyz3(x, У, z)) ,mcix(nXYZ2(x,y,zp (цXYZ4(x,y,z)),(x,y,z') eXxYxZ I Union: A (M-XYZ1 > M-XZ Z2 ) UВ (HXYZ3 ,HxyZ4) Г (х, у, z), т ax(nXYZt (х, у, z), nXYZ3 (х, у, 1 т in (hxyz2 (х, у, z), ^xyz4 (х, у, z)), (х, у, z) Е X х У х Z z )),' } ( (х,у, z), (min(1,1) ,min(1,1), min(1,1)),) (max(0,0), max(0,0), max(0, -) j = {(х, у, z), (1,1,1), (0,0,1)} Let us consider a cuboid that stands in the xyz-plane such that | portion of the region is occupied by the dark region of water shown in the following figure: Fig. 2. Three dimensional imprecise number with membership value ((1-0)х(1-0)х(|-|)) = 0 to form a null or empty set. Union: 5(ЦхYz(x,у,z)) U E (цcXYZ(x,у,z)) = {(х, у, z), (1,1,1), (0,0,0)} U {(х, у, z), (1,1,1), (0,0,1)} f(x,у,z), (max(1,1) ,тах(1,1), max(1,-)),) (min(0,0),min(0,0),min(0,-) j = {(х, у, z), (1,1,1), (0,0,0)} with the membership value ((1 - 0) х (1 - 0) х (1 - 0)) = 1 Here, the membership function of cuboid is E(ЦхYz(x,У,z)) = {(х,у,z),(1,1,1* ,(0,0,0)} with membership value to form the universal set. Thus by the help of graphical it can be introduced property of three dimensional imprecise numbers, A. Property- ((1 - 0) х (1 - 0) х (1-0)) = 1 and And the membership function of the complementary part is, А С“сх^(х,у^)) = {х,у, z),(1,1,1),(0,0,—*} with membership value ((1-0)х(1-0)х(1-1)) = 1 Now intersection and the union of three dimensional imprecise numbers are the following: Intersection: GuхYz(x,у,z)) П E (цСх1,.,(х,у^)) (х,у, z), 1,1,1), (0,0,0) • и (х,у, z), (1,1,1), (0,0,1 (ii) №хYz(x,У,z)) U Л(цхYZC(x,У,z)) = П, where 0 and П are null and universal respectively. B. Property- Commutative laws Let ^((^XYZl (х, у, z)) = {(х, у, z), ^XYZI (х, у, z), ^XYZ2 (х, у, z): (х, у, z) Е X х Y х Z} and S№хYZ2(x,У,z)) = {(x,у,z),ЦхYZз(x,у,z), ЦхYZ4(x,у,z): (x,у,z) Е X х У х Z} be two dimensional imprecise numbers. Then (i) (( ( , , )) U (( ( , , )) = В (Guxyz2 (х, у, z)) U Л (Guxyzl (х, у, z)) Proof- If и 1 1 1\ 1 1 1 ) A №xyz 1(х, у, Z) = W^,^,^),^^,^,^)} and 111 111 в (feYZ2(x,y,z)) {(з,3,3),(6,6,6)} be two dimensional imprecise numbers, then A((HXYZl(x,y,z)) U B((^xYZ2(X,y,z)') f(max(|,l),maxC|,l),max^ = [ („„(-^.mm^),,™^)) -Kl-l-D-Cl-i-i)} = f(min (34),min (l 4),min (l 4)) 1 ( (m«x(i,4),max(i,4),max(i,4))) ={(l,l,l),(4,4,9} Hence proved C. Property- Distributive Laws If ^№xYZi(x,y,z)) , B((^xYZ2(x,y,z)) and C((^xYZ3(x,y, z)) be three two dimensional imprecise number, then (i) ^№xYZi(x,y,z)) П (B((^xyz2 (x,У, z))C(Guxyz3 (x,У, z)» - ^(G«xyzi (x, у, z)) П B ((uxYZ2 (x, у, z)) UЛ((^xYZ1(x,У,z)) П C((^xYZ3(x,y,z)) And №xYZ2(x,y)) U ^((^xYZ1(x,y)) = ((maX(|-|),max(|,|),max(|,|)),j l (mi^(i,4),mi^(i,4),min(i,|)) J -{(l-l-l),(i,i-i)} Hence proved (ii) ^((BxYZi(x,y,z)) U (B(GuxYZ2(xyz)) П C((^xYZ3(x,y,z))) - 4((jUxYZi(x,y,z)) U B((^xYZ2(x,y,z)) n Л((лxYZ1(x,У,z)) U C((^xYZ3(x,y,z)) Let us prove the property (i) and (ii) with example. If ^Zi^»-^ ( (4,4,4) ) (ii) ^№xyzi (x, у, Z)) n B ((^XYZ2 (x, У, z)) - B((^xYZ2(x,y,z)) nЛ((лxYZ1(x,У,z)) B№xYZ,(X-,.z))-[(lll)-(l-l.l)j Proof: If and (1,1,1),) ^(Guxyz i(x,y,z)) - j^ 21 2/ } (4,4,4)) - л.. x у .:{: \ : ( - .: Then and «((«v.^U-v,z)) {(3,3,3),(6,6,6)} ^№xYZi(x,y,z)) n (B((^xYZ2(x,y)) U C((^xYZ3(x,y,z))) be two dimensional imprecise numbers, then / And ^((BxYZi(x,y,z)) П B((^xYZ2(x,y,z)) М!#^^!),^^ ((шм (4, i), m«x (4, i), m«x(4, i)) J ={(l,l,l),(4,4,4)} ((212)1 l(4-4■4)ln| ^H.im maxCl■i)- • B((^xYZ2(x,y,z)) n Л((^xYZ1(x,У,z)) \ \max(li)/ MIDI m-C2^2)-[l-nClj)/] / -{(2,2,2),(4,4,4)}n{(l,l,l),(7,7,7)} ⎪⎧(min(12,13*,min(12,13*,min(12,13**,⎪⎫ ⎪⎨(max(4,7*,max(4,7*,max(4, 7*)⎪ ={(13,13,13*,(14,14,14*} And A (( MxYZl (X,У,Z))∩В (( MXYZ2 (X,У,Z))∪A((MXYZ1 (X,У,Z))∩C (( MXYZ3 (X,У,Z)) ⎪⎧(min(12,13*,min(12,13*,min(12,13**,⎪⎫⎪⎨ (max(14,15*,max(14,15*,max(14,15*)⎪⎬ ∪ (min(12,16*,min(12,16*,min(12,16**,⎪⎫ ( max(4,7*,max(4,7*,max(4, 7*)⎪ (13,13,13*, (16,16,16*, (14,14,14* (14,14,14* ⎪⎧(max(13,16*, max(13,16*,max(3,6**,⎪⎪⎨(min(4,4*,min(4,4*,min(4,4*)⎪ ={(13,13,13*,(14,14,14*} Hence proved (i) And A((μXYZl(x, y)) ∪(Β((μXYZ2(x, y)) ∩Ϲ((μXYZ3 (x, y))) ⎧⎛min(13,16*,⎞⎫⎪⎪⎜⎜min(13,16*,⎟⎟,⎪⎪ ⎝min(3,6*⎠ (12,12,12*, ⎪⎝min(13,16*⎠ (14,14,14* ⎪⎨ max(315,617*, ⎪⎪⎪⎜⎜max(15,17*,⎟⎟⎪⎪⎪ ⎩⎪⎝max (515,717*⎠⎭⎪⎪ ={(12,12,12*,(14,14,14*}∪{(16,16,16*,(15,15,15*} ⎪⎧(max(12,16*, max(12,16*,max(2,6*),⎪ = ⎩⎪(min(14,15*,min(14,15*,min(14,15*)⎭⎪ ={(12,12,12*,(15,15,15*} And A (( MXYZ1 (X,У,Z))∪В (( MXYZ2 (X,У,Z)) ∩A((MXYZ1 (X,У))∪C (( MXYZ3 (X,У,Z)) (max(12,13*,max(12,13*,max(12,13**,⎪⎫(min(14,15*,min(14,15*,min(14,15*)⎪⎬ ⎪⎧(max(12,16*, max(12,16*,max(12,16**,⎪⎫ ⎪⎨ ( min(4,7*,min(4,7*,min(4,7*)⎪ ={(12,12,12*,(15,15,15*}∩{(12,12,12*,(17,17,17*} (min(12,12*,min(12,12*,min(12,12**,⎪⎫ (max(1,1*,max(1,1*,max(1,1*)⎪⎬ ={(12,12,12*,(15,15,15*} Hence proved (ii) Further it can be verified that the following properties of classical sets are satisfied by the three-dimensional imprecise sets A( Mxyz (x,У,z)), В( MXYZ (X,У,z)) and C(Ц-XYZ (X,У,Z)): D. Idempotent Laws (i) A(μXYZ(x, y, z)) ∪А(μXYZ (x, y, z)) = A(μXYZ (x, y, z)) (ii) A(μXYZ(x, y, z)) ∪А(μXYZ (x, y, z)) = A(μXYZ (x, y, z)) E. Associative Laws Β(μXYZ (x, y, z)) (i) A(μ ,, ∪Ϲ(μ (x, y, z)) = (A(μXYZ(x, y, z)) ∪В(μXYZ (x, y, z))) ∪Ϲ(μXYZ (x, y, z))) / , В(MXYZ(X,У,Z)) (ii) A(MXYZ(X,У,Z))∩( ) ∩ ( ( ,У, )) =(A(MXYZ (X,У,Z))∩В(MXYZ (X,У,Z))) ∩C(M-XYZ (X,У,Z))) F. De Morgan’s Law: (i) (A(M-XYZ (X,У,Z))∪В(MxYZ (X,У,Z))) =(I^XYC (X,У,Z))∩В(I^XYC (X,У,Z)) (ii) (A(MXYZ (X,У,Z))∩В(MXYZ (X,У,Z))) =(HXYC (X,У,Z))∪В(HxYC (X,У,Z)) V. Conclusion As the solution of practical problem is the main objective of this article. So the possible effect of fuzziness of any particle is suggested to study along all the axes. If the problem is solved in one part of the axis may not be overcome for whole the body because of not study of other part of the body. All types of imprecise numbers are considered as usual set to have same characters and properties. So, known characters of the classical sets are helped to identify the characters of the above mentioned imprecise numbers. Operations of intersection and union of sets are the tools to prove of the above properties. Maximum and minimum operators are the operations of union and intersection in the above sections of the article. Other properties based on the remaining operations of classical set are left for future study. Acknowlegement Author would like thanks the anonymous reviewers for careful reading of this article and for their helpful comments which have improved this work.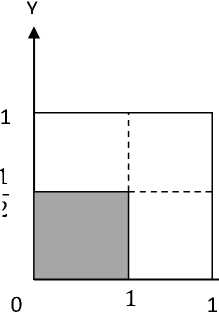
Список литературы An Introduction of Two and Three Dimensional Imprecise Numbers
- L.A. Zadeh, Fuzzy sets, Inform. And Control, 1965, 8, 338-353.
- C. H. Cheng, a new approach to ranking fuzzy numbers by distance method, Fuzzy Sets and systems, 95, 1998, 307-317.
- H.K. Baruah, Theory of fuzzy sets: Beliefs and realities, I.J. Energy Information and Communications. 2(2), (2011), 1-22.
- H.K. Baruah, Construction of membership Function of a Fuzzy Number, ICIC Express Letters 5(2), (2011), 545-549.
- H.K. Baruah, In search of the roots of fuzziness: the Measure Meaning of partial Presence, Annals of Fuzzy mathematics and informatics. 2(1), (2011), 57-68.
- S. K. Sardar and S.K. Majumder, On Cartesian Product of Fuzzy Completely Prime and Fuzzy Completely Semi-prime Ideal of Semi-groups, I.J. of Computational Cognition, Vol. 9, 2011.
- Muralikrishna P. and Chandram-ouleeswaran M., Generalisation of Cartesian product of Inttuitionistic L-Fuzzy BF-Ideals, I.J. Contemp. Maths. Sciences, Vol. 6, 2011, no.14, 671-679.
- H.K. Baruah, An introduction theory of imprecise Sets: The Mathematics of partial presence, J. Math. Computer Science 2(2), (2012), 110-124.
- A. Varghese and S. Kuriakose, Cartesian Product Over Intuitionistic Fuzzy Sets, International Journal of Fuzzy Sets, Vol.2, 2012, 21-27.
- M. Dhar, On Geometrical Representation of Fuzzy numbers, IJEIC, Korea, Vol.3, Issue 2, 2012, P-29-34.
- M. Dhar, The compliment of fuzzy numbers: An Exposition, Intelligent system and Applications, 2013, 08, 73-82.
- M. Dhar and H.K. Baruah, Theory of Fuzzy Sets: An Overview, I.J. Information Engineering and Electronic Business, 2013, 3, 22-33.
- M. Dhar, A Note on Determinant of Square Fuzzy matrix, I.J. Information Engineering and Electronic Business,2013,1,52-59.
- S. Broumi, F. Smarandache and M. Dhar, On Fuzzy Soft Matrix based on reference Function, I.J. Information Engineering and Electronic Business,2013,2,26-32.
- Priya T. and Ramachandran T., Homomorphism and Cartesian Product of Fuzzy PS-Algebra, Applied Mathematical science, Vol. 8, 2014, no. 16, 3321-3330.
- S. Borgoyary, A Few Applications of Imprecise Matrices, I.J. Intelligent system and Applications, 2015, 08, 9-17.


