An TPM based approach for generation of secret key
Автор: Sanjay Kr. Pal, Shubham Mishra
Журнал: International Journal of Computer Network and Information Security @ijcnis
Статья в выпуске: 10 vol.11, 2019 года.
Бесплатный доступ
As the world becoming so much internet de-pendent and near about all the communications are done via internet, so the security of the communicating data is to be enhanced accordingly. For these purpose many encryption-decryption algorithms are available and many neural network based keys are also available which is used in these algorithms. Neural Network is a technique which is designed to work like a human brain. It has the ability to perform complex calculations with ease. To generate a secret key using neural networks many techniques are available like Tree Parity Machine (TPM) and many others. In TPM there are some flaws like less randomness, less time efficient. There are already three rules available i.e. Hebbian Rule, Anti Hebbian Rule and Random Walk, with same problems. So to overcome these issues, we propose a new approach based on the same concept(TPM, as Tree-structured Neural Network’s execution time is comparatively less than that of the other Neural Networks) which generate random and time-efficient secret key.
Artificial Neural Networks, Tree Parity Machine (TPM), Cryptography, Secret Key, Key Ex-change
Короткий адрес: https://sciup.org/15015721
IDR: 15015721 | DOI: 10.5815/ijcnis.2019.10.06
Текст научной статьи An TPM based approach for generation of secret key
Published Online October 2019 in MECS DOI: 10.5815/ijcnis.2019.10.06
To remove this problem the key is generated using artificial neural networks which overcomes that issues, the basic process of how ANN works ,i.e., in artificial neural network, both the communicating networks receive an identical input vector, generate an output bit and are trained based on the output bit [15]. The dynamics of the two networks and their weight vectors is found to exhibit a novel phenomenon, where the networks synchronize to a state with identical time-dependent weights. This concept of synchronization by mutual learning can be applied to a secret key exchange protocol over a public channel [9] based on that many techniques are developed. One of the technique is TPM (Tree Parity Machine) where we can generate a secret key following some rules i.e. Hebbian Rule, Anti Hebbian Rule, and Random Walk and it is random in nature but its randomness is not strong it can be easily get detected with some combinations and also generating key using above rules is bit time consuming. To solve this problem we have proposed a method of generating a secret key using TPM which is more random in nature and also time efficient compare to other TPM rules.
-
II. Related Work
There are several numbers of key generating algorithm available, it is quite difficult to say one the best because as it varies to situations. An algorithm which is appropriate for one situation can be inappropriate for another. Besides these facts, there are certain parameters which assist in selecting the correct algorithm. The basic factors upon which the comparison have been taken are execution time and time complexity of the algorithm. As on generating a secret key using available rules of Tree Parity Machine, the resultant graph of the comparison between Non-Neural and Neural Network, it is clear that the generated key is random [5]. Key generation using TPM and Double Hidden Layer Perceptron(DHLP), together it gives more security to the key as TPM works on a single hidden layer and DHLP uses double hidden layer and also space complexity get optimized[15]. Using the Cuckoo Search algorithm for a key generation will give optimal weight for better synchronization [14]. The proposed algorithm is compared with the available rules of Tree Parity Machine. With the same complexity and up-gradation in security level, it, as a result, increased high randomness in key generation. Last but not least, the average execution time for generating the key is better than the available rules which give the reason to the proposed technique to be most adorable.
-
III. Terminology
Before going into detail discussion of the topic first get familiar with some terminologies. A brief explanation of these terminologies help you to understand the whole paper without any doubt.
-
A. Artificial Neural Network
Artificial Neural Networks (ANN) are the pieces of a computing system designed to simulate the way the human brain analyzes and processes information. ANNs are composed of multiple nodes, which imitate biological neurons of human brain [2]. The human brain is composed of 86 billion nerve cells called neurons. The neurons are connected by links and they interact with each other. The nodes can take input data and perform simple operations on the data. The result of these operations is passed to other neurons. The output at each node is called its activation or node value. Each link is associated with weight [11]. ANN have self-learning capabilities that enable them to produce better results as more data become available.
-
B. Tree Parity Machine
A Tree Parity Machine or TPM is a multilayer feedforward neural network. A feed-forward neural network is an ANN in which the connections between the units do not form a loop. It is one of the first and simplest types of artificial neural networks and the information moves in only one direction, i.e., forward. The data moves from the input notes to the hidden nodes and finally from the hid- den nodes to the output nodes. There are no cycles or loops in this network [3].
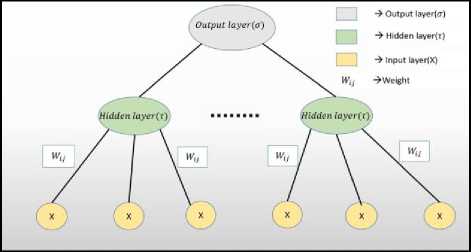
Fig.1. Basic Structure of Tree Parity Machine (TPM)
A TPM is a special type of feed-forward multi-layered ANN, where is 1 output neuron, K hidden neurons, and K*N input neurons.
The input layer of TPM can take any values i.e. x ij =
-
1, 2, 3, 4,….,N
The weight of edge between input and hidden layer are in range of {-L,...., 0 ,....L}
The output of the hidden layer is calculated by the sum of multiplication of no. of inputs and no. of weights, which is denoted by sigma( ), mathematically it is shown as
^ i = sgn ( E N = 1 W ij X y ) (1)
As signum function is used in the formula, signum function returns {-1, 0, 1} sgn(x)={-1 if x<0, 0 if x=0, 1 if x>1} Where sgn(x)=signum(x)
If the scalar product is less than 0, then the output of the hidden neuron is mapped to -1and if the scalar product is equal to 0, then the output of the hidden neuron is mapped to 0 and if the scalar product is greater than 0, then the output is 1. After that the output of the neural network is then computed as the multiplication of all values produced by hidden elements:
T = n K1 CT (2)
The output of the tree parity machine is binary and it is denoted by tau ( t ) [14].
-
C. Cryptography
Cryptography is the study and practice of secure transmission of messages from the adversaries. The main work of cryptography is to keep the original data secured by manipulating it in such a way that no meaningful data can be derived from it until the manipulation is reversed. In information security, it is about constructing protocols and algorithms that will keep the third parties from reading private messages between the sender and receiver
-
[12] . In general, cryptography is the art and science of converting a meaningful text to utter nonsense to prevent the third party readability. It can only be transformed back to its original state by the means of a key [3].
-
D. Secret Key
Secret key cryptography methods employ a single key for both encryption and decryption. The sender uses the key to encrypt the plaintext and sends the cipher text to the receiver. The receiver applies the same key to decrypt the message and recover the plaintext. Because a single key is used for both functions, secret key cryptography is also called symmetric encryption [4].
-
E. Private Key
Private key is a key where only single key is used for both encryption and decryption process. Before the Transmission of information starts the key distribution has to be made [10]. Example: DES, 3DES, BLOWFISH, AES etc.
-
F. Public Key
Public key is a key where two different key is used one key for encryption and another key for decryption [13]. Example: RSA, Elgamal Signature, Diffie Hellman key exchange, Digital signature etc.
-
IV. Traditional Generation of Seceret Key Using Tree Parity Machine with Algorithm
One of the most popular model of neural networks which are used as communicating channel is the Tree Parity Machine (TPM). The TPM is a special type of multi-layer feed-forward neural network [11].
The Tree Parity Machine structure is comprised of three layers i.e. input layer, hidden layer and output layer and for synchronization two TPMs are used.
The input layer of TPM can take any values i.e. X y = 1,2,3,4...., N. The weight of an edge between the input layer and the hidden layer is also required that is of range {-L,.., 0 ,..., L}.
The output of the hidden layer is calculated by taking sum after multiplying the no. of inputs and no. of weights, mathematically it is shown in (1 .
As signum function is used in the formula, signum function returns {-1, 0, 1} sgn(x)={-1 if x<0, 0 if x=0, 1 if x>1}
If the scalar product is less than 0, then the output of the hidden neuron is mapped to -1and if the scalar product is equal to 0, then the output of the hidden neuron is mapped to 0 and if the scalar product is greater than 0, then the output of the hidden neuron is 1. After that the output of the neural network is then computed as the multiplication of all values produced by hidden elements mathematically in (2).
The output then produced from both TPMs if they are same then it will proceed further if not then it has to re- peat it from modifying the weight used in the hidden layer. If the value of the output layer of both TPMs are same which means the weights are synchronized to each other, then the weight of TPMs are updated with the following given rules-
Hebbian rule: Wy = Wy + Xy *ci(3)
Anti- Hebbian rule: Wy = Wy -X y *ci(4)
Random Walk rule: Wh = Wh + XH(5)
ij ijij
When the updated weights become the same in both TPMs then that will become the secret key.
The different stages in the secret key generation procedure which is based on traditional TPM can be stated as follow [5]:
Step 1: Take two Tree Parity Machine to say, TPM-A and TPM-B.
Step 2: Initialize the weight of the edge between the input node and hidden node in a range of {-L ...., 0 ,......,
L}
Step 3: Put your desired input on the input node i.e. 1,2,3,4,…,N.
Step 4: Find the value of a hidden layer which is denoted by sigma ( с ) by putting the value of inputs and weights using (1).
Step 5: After finding sigma ( с ) value find the output layer of both TPMs which is denoted by tao ( т ) using (2).
Step 6: if the output of TPM-A and TPM-B is same then go to Step 7 if not go to Step 2.
Step 7: when the output of TPM-A and TPM-B becomes same then update the weight with any one of the following rule -
-
a. Hebbian Rule b. Anti-Hebbian Rule c. Random Walk.
Step 8: When the updated weight in TPM-A and TPM-B becomes same then that weight become secret key of the input.
-
V. Proposed Rule with Algorithm
In this proposed study we have taken two TPMs i.e. TPM-A and TPM-B and initialize the weight of edges between the input node and hidden node in the range of {-L,...,0,..., L} and user will enter their desired values in input node. Then find the hidden layer by using formula (1). After finding the hidden layer of both TPMs find the output layer by using (2). If the output value of both TPMs is same then we can say that TPMs are synchronized to each other else weights are to be updated to make them synchronize. After synchronization update the weight using (6). Now to make the weights random each time we have taken modulus of updated weight and the current local time. The output of the modulus will generate random and strong secret key, which will be unique each time.
Algorithm of above explained concept:
Step 1: Take two Tree Parity Machines (TPM) to say, TPM-A and TPM-B.
Step 2: Initialize the weight of the edges between the input node and the hidden node in a range of {-L ....,0,...
L}
Step 3: Put your desired values on the input node i.e. 1, 2, 3, 4… N.
Step 4: Find the value of a hidden layer which is denoted by sigma ( с ) by putting the value of inputs and weights using (1).
Step 5: After finding the values of sigma ( с ) find the output layer for both TPMs denoted by tao ( т ) which is also known as synchronized data using (2).
Step 6: If the output of TPM-A and TPM-B is same then go to step 7 else go to step 2.
Step 7: When the output of TPM-A and TPM-B becomes same then update the weight with the Proposed Rule:
W y = Wy + т (6)
Step 8: When the updated weight in TPM-A and TPM-B becomes equal then again modify the weight by taking modulus of latest updated weight and current local time which will make the weight random each time whenever it is called. This updated weight become the secret key.
W y = W y % current time (7)
-
VI. Execution Of Rule Practically with Real Data
-
A. Complexity Analysis
Execution time of the algorithms depends on the values of input. So to examine the fact, we have given same input value for all the four rules (Hebbian, Anti Hebbian, Random Walk and Proposed Rule). Let suppose the input value is 2500 (i.e., maximum value of weight is 2500). Now the values of sigma ( с )is calculated and then the values of tau ( т ). If the output values of ( т ) are same as per algorithms then the output thus received is treated as synchronized data. Then the data will be passed through all the four rules and thus the output received i.e. secret key’s execution time is different for all the rules. For example, Hebbian's time is 2 sec, Anti Hebbian's time is 2.03 sec, Random Walk's time is 2.108 sec and proposed rule's time is 0.265 sec . As the execution time is different for the given value of input, similarly for different values of input execution time and iteration of program will also be different. So the complexity of all four rules are O(n). But the average time taken for different sets of input values given in Table 1 by proposed rule is lesser than the average time taken by the other traditional rules. Hence we can say that the proposed rule is a bit faster in executing secret key than other traditional TPM rules.
-
B. Experimental Comparison between traditional and proposed rule
The experimental result of all the algorithms are examined using Intel ® Core™ i3 processor and the supported system is a 64 bit machine with 4GB RAM capability [6]. All the algorithms are implemented as well as executed in C programming language. The main part which is implemented of the proposed algorithm is:
for (i = 0; i < n; i++){ if (updated_weight_a[i] = = updated_weight_b[i]){ key[i] = local_time % updated_weight_a[i];
printf ("Secret key is %d \n", key[i]);
} else goto update_weight;
} update_weight:
for (i = 0; i < n; i++){ weight_a[i] = i; weight_b[i] = i;
}
The experimental results are presented in tabular form as well as in graphical form to make the clear understanding of the execution of the different algorithm for different values of the weight [6]. In Table 1 the first column represents the length of weight to be taken, the second column represents the execution of Hebbian Rule, the third column represents the execution of Anti Hebbi-an Rule, the fourth column represents the execution of Random Walk Rule, the fifth column represents the execution of Proposed Rule respectively and the last row shows the average time taken by all the rules in total input values.
Table 1. For all algorithms tested with given sets of input weights, execution time is recorded in second.
|
Weight_Input |
Hebbian Rule |
Anti-Hebbian Rule |
Random Walk |
Proposed Rule |
|
150 |
0.14 |
0.125 |
0.125 |
0.125 |
|
300 |
0.25 |
0.266 |
0.25 |
0.297 |
|
450 |
0.359 |
0.359 |
0.36 |
0.375 |
|
1000 |
0.86 |
0.796 |
0.844 |
0.797 |
|
2500 |
2.0 |
2.03 |
2.108 |
0.265 |
|
4000 |
1.156 |
1.172 |
1.109 |
0.391 |
|
5500 |
0.531 |
0.531 |
0.578 |
0.515 |
|
7000 |
0.687 |
0.672 |
0.656 |
0.671 |
|
8500 |
0.796 |
0.797 |
0.796 |
0.812 |
|
10000 |
0.984 |
0.953 |
0.953 |
0.938 |
|
11500 |
1.093 |
1.094 |
1.094 |
1.094 |
|
13000 |
1.218 |
1.219 |
1.25 |
1.234 |
|
14500 |
1.359 |
1.375 |
1.375 |
1.406 |
|
Avg. Time Taken |
0.8794 |
0.8760 |
0.8844 |
0.6861 |
-
C. Graphical Representation of Executed Data
This is a graphical representation of tabular data showing variations in time required for executing secret key by changing the weight inputs.
In this (Fig.2.) the x-axis denotes weight inputs and y-axis denotes time-taken for execution and different shades denotes the different algorithms.
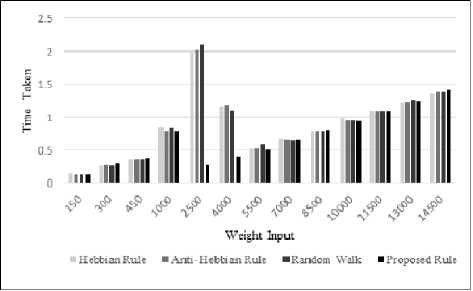
Fig.2. Graphical Representation of Executed Data
-
VII. Conclusion
A secret key is helpful for protecting data transferring over the networks. So in above proposed paper it is shown a new modified rule which is made based on Tree Parity Machine with the current time concept i.e. the value of key changes dynamically when user give different input. This concept make little bit impossible to the intruder to catch the secret key as it is changing in every second and this will help to encrypt the data and transmit from one user to another more securely and fast. In future, it can be upgraded to reduce the time complexity of the proposed algorithm i.e. less than O(n). Here, input are taken in numeric but in future the input may be taken as alpha-numeric or special characters.
Список литературы An TPM based approach for generation of secret key
- W.Diffie and M.E.Hellman, “New directions in cryptog-raphy”, IEEE Transactions on Information Theory, vol. 22, pp.644-654, November 1976. DOI: 10.1109/TIT.1976.1055638
- Nashaat El-Khamisy Mohamed and Ahmed Shawky Morsi El-Bhrawy, "Artificial Neural Networks in Data Mining", IOSR Journal of Computer Engineering, vol. 18, pp. 55-59, December 2016. DOI: 10.9790/0661-1806035559
- Sanjay Kumar Pal and Sumeet Anand, "Cryptography Based on RGB Color Channels using ANNs", I. J. Com-puter Network and Information Security, vol. 5, pp. 60-69, May 2018. DOI: 10.5815/ijcnis.2018.05.07
- Shakeel Ahmad Dar, "RSA Algorithm Key Generation Extension", International Journal of Modern Trends in Engineering and Research, vol. 5, pp. 73-75, January 2018. DOI: 10.21884/IJMTER.2018.5013.DAYGS
- R.M.Jogdand and Sahana S.Bisalapur, "Design Of An Efficient Neural Key Generation", International Journal of Artificial Intelligence & Applications, vol. 2, pp. 60-69, January 2011. DOI: 10.5121/ijaia.2011.2105
- Sanjay Kr. Pal and Nupur Chakraborty, "Application of Cosmos’s law of Merge and Split for Data Encryption", I. J. Computer Network and Information Security, vol. 5 , pp. 11-20 , May 2017. DOI: 10.5815/ijcnis.2017.05.02
- Om Pal and Bashir Alam , "Diffie-Hellman Key Exchange Protocol with Entities Authentication", International Journal Of Engineering And Computer Science, vol. 6,pp. 20831-20839, April 2017. DOI: 10.18535/ijecs/v6i4.06
- Shengbao Wang, Zhenfu Cao, Maurizio Adriano Strangio and Lihua Wang, "Cryptanalysis and improvement of an elliptic curve Diffie-Hellman key agreement protocol", IEEE Communications Letters, vol.12, pp. 149-151, Feb-ruary 2008. DOI: 10.1109/LCOMM.2008.071307
- Mehdi Mirzaey, Mohammad (Behdad) Jamshidi and Yousef Hojatpour, "Applications of Artificial Neural Networks in Information System of Management Ac-counting", International Journal of Mechatronics,Electrical and Computer Technology, vol. 7 , pp. 3523-3530 , July 2017. DOI: IJMEC/10.225141
- Srinivasan Nagaraj, G.S.V.P.Raju and V.Srinadth, "Data Encryption and Authentication Using Public Key Ap-proach", Procedia Computer Science, vol. 48, pp. 126-132, May 2015. DOI: https://doi.org/10.1016/j.procs.2015.04.161
- Jonathan Martínez Padilla, Uwe Meyer-Baese and Simon Foo, "Security evaluation of Tree Parity Re-keying Ma-chine implementations utilizing side-channel emissions", EURASIP Journal on Information Security, vol. 3, pp. 1-16, March 2018. DOI: https://doi.org/10.1186/s13635-018-0073-z
- Sanjay Kumar Pal and Suman De, "An Encryption Tech-nique based upon Encoded Multiplier with Controlled Generation of Random Numbers", I. J. Computer Network and Information Security, vol. 7, pp. 50-57, September 2015. DOI: 10.5815/ijcnis.2015.10.06
- Aysha Albarqi, Ethar Alzaid, Fatimah Al Ghamdi, Somaya Asiri and Jayaprakash Kar, "Public Key Infrastructure: A Survey", Journal of Information Security, vol. 6, pp. 31-37, January 2015. DOI: 10.4236/jis.2015.61004
- Shikha Gupta, Nalin Nanda, Naman Chhikara, Nishi Gupta and Satbir Jain, "Mutual Learning In Tree Parity Machines Using Cuckoo Search Algorithm For Secure Public Key Exchange", ICTACT Journal on Soft Computing, vol. 8, pp.1663-1667, April 2018. DOI: 10.21917/ijsc.2018.0231
- Arindam Sarkar and Jyotsna Kumar Mandal, "Comparative Analysis of Tree Parity Machine and Double Hidden Layer Perceptron Based Session Key Exchange in Wireless Communication", Emerging ITC for Bridging the Future-Proceedings of the 49th Annual Convention of the Computer Society of India, vol. 337, pp. 53-61, January 2015. DOI: 10.1007/978-3-319-13728-5_6
- Surinder Kaur, Pooja Bharadwaj and Shivani Mankotia, "Study of Multi-Level Cryptography Algorithm: Multi-Prime RSA and DES", International Journal of Computer Network and Information Security, vol. 9, pp. 22-29, September 2017. DOI: 10.5815/ijcnis.2017.09.03


