An Ultra-secure Router-to-router Spontaneous Key Exchange System

Published Online June 2015 in MECS

Securing information is an increasingly important need of the modern society. As computing power increases, the ability to launch successful cryptanalytic attacks correspondingly increases. This has led to using longer and longer keys in either symmetric (e.g., AES-based) or asymmetric (e.g., RSA-based) cryptography systems, or more frequent key exchanges, or both. Neither of these or for that matter any contemporary cryptographic technique used on a commercial basis offers unconditional security. Furthermore, distribution and management of keys continues to remain an important part of the security process constituting a significant portion of the overall cost of security.

Classically, the one-time pad proposed by an Army Signal Corp officer, Joseph Mauborgne [1,2] is the only encryption scheme that offers perfect security. The onetime pad is a symmetric encryption scheme where a random key of length equal to the transmitted message is used for both encryption and decryption. Since each new message requires the use of a new random key, the onetime pad is known to be unbreakable. However, distributing keys securely between the two communicating endpoints with a length equal to the message is a requirement that cannot be practically met.

This paper proposes a novel means of distributing secure keys on a point-to-point basis between two routers that does not require any human or machine intervention. The communicating routers can exchange keys at random intervals or on a message or a session basis; indeed, based on any scheme that the customer wishes to have. The proposed scheme is independent of the medium of transmission between the two routers and does not necessitate the absence of intermediate repeaters between the routers. Intermediate repeaters are unacceptable in a contemporary quantum key distribution system. The cryptography system proposed in this paper is based on a multi-stage protocol requiring an exchange of keys between the two communicating parties in one or more steps.

A mechanical representation of the proposed system is as follows: Alice uses a lockbox with two latches, each of which can be independently locked and opened by the respective key holder. Alice puts her message in the box and a lock of her own on one of the two latches on the box. Bob receives the box and puts his own lock on the other latch, without trying to open the box. He then sends the box back to Alice. Upon receiving the box, Alice unlocks her lock and returns the box to Bob. She cannot, of course, open the box because Bob’s lock is still there on the box. On the second trip of the box from Alice to Bob, the box has only Bob’s lock which he can then unlock upon receiving it and retrieve the message inside the box.

The difference between the above example and the proposed scheme is that unlike the mechanical representation where we have assumed that the lock is secure, electronic bits (or their photonic representation) can be easily copied by an intruder. This has two implications. First, the message to be transmitted cannot be in the open. Second, even if this message were to be altered by some form of encryption, since the intruder can have access to each of the three legs of transmission; the encryption mechanism needs to be sufficiently robust in order to thwart an attempt to recover the message during transition. This paper presents a system based on discrete logarithms for securing the messages in transition. The proposed system is best suited for exchanging keys between two routers and can be done as frequently as necessary and can be initiated by either of the two communicating entities.

This paper is organized as follows: Section II captures the mathematical foundations of the proposed scheme based on the use of discrete logarithms as well as key distribution protocols previously used. Section III discusses the proposed technique and its cryptographic strength. Section IV introduces another contrivances that can further enhance the cryptographic strength of the proposed protocol. Section V effects a comparison with the currently available QKD systems and Section VI captures our conclusions.

• II. R elated W ork

• A.    Discrete Logarithms

Discrete logarithms constitute a well-known technique in number theory [3,4]. Discrete logarithms in Z _p are related to the primitive roots of the prime number p. All prime numbers have primitive roots. One characteristic of a primitive root a of a prime number p is that successive powers of a from 1 to p — 1 mod( p) generate the numbers from 1 to p — 1, all of which are distinct, but in some unpredictable order. In other words, for any integer b and a primitive root a of a prime number p, there is a unique exponent i such that,

b = almod(p)    0 < i < p — 1       (1)

The exponent i is referred to as the discrete logarithm of the number b for the base a mod p.

One of the properties of discrete logarithms is that, given a, i, and p, the computation of b is easy. However, given b and a , computation of i is difficult. This difficulty is of the same order of magnitude as factoring primes required for RSA [5]. We note that unlike the Diffie-Hellman technique (discussed in the next subsection), these parameters are not global. They are known only to the concerned router pairs.

We derive our clue from the fact that if the information to be transmitted (in other words, the key) gets embedded in the exponent i (or the discrete logarithm) and is transmitted as the number b, deriving the key will be as hard as any contemporary encryption scheme. This combined with the fact that the key exchange can take place as frequently as desired with minimal overhead in communication, we posit that the proposed scheme has the potential of approaching the level of security of contemporary quantum key distribution (QKD) systems. The following section discusses one of the contemporary key management/distribution protocols.

• B.    Contemporary Key Distribution Protocols

In this section, the Diffie-Hellman key distribution [6,7] technique is discussed. The Diffie-Hellman key distribution algorithm is based on using prime numbers as well as primitive roots in a similar context as in the proposed multi-stage protocol.

Fig. 1 summarizes the Diffie-Hellman key exchange algorithm. In this scheme, there are two publicly known numbers (global elements); q is a prime number with its primitive root a. XA and XB are two random variables chosen by Alice and Bob, respectively. Using the key exchange system presented in Fig. 1, Alice and Bob will share a key К = (YB)XAmod(q) = (YA)XBmod(q).

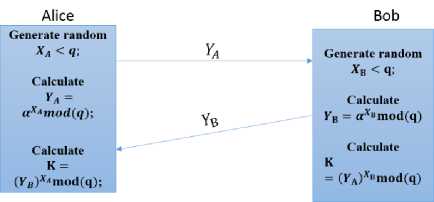
Fig. 1. Diffie-Hellman key exchange

The Diffie-Hellman key exchange algorithm depicted in Fig. 1 is, however, vulnerable to the man in the middle attack. An attacker, Eve, will proceed as shown in Fig. 2 to share a key К 1 with Alice and another key К 2 with Bob. Thus, all future communication between Alice and Bob is compromised.

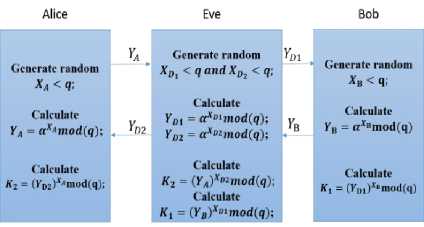
Fig. 2. Man in the middle attack in case of a Diffie-Hellman key exchange system

Shared keys between different parties in a network can also be established with the help of a trusted third party. This third party is called the key distribution center [8]. Furthermore, symmetric key distribution using asymmetric encryption can be used as a key distribution scheme as proposed in [9] and [10]. It is worth noting that the scheme proposed in [9] is vulnerable to the man in the middle attack, whereas the scheme proposed in [10] assumes that Alice and Bob already exchanged a public key using a public key distribution technique. Several public key distribution techniques can be used, e.g., public announcement, publicly available directory, public-key authority, and public certificate.

The protocol proposed in this paper overcomes the overhead of maintaining an updated list of the public keys of each node in the network as well as sharing them globally by the means mentioned earlier. We do note that the proposed system, however, is deployed for encrypting messages on a link which connects two routers. It does not offer an end-to-end application level encryption scheme.

• III.    T he P roposed P rotocol

In this section, the proposed protocol which is a multistage router to router key distribution protocol is presented. The proposed protocol is a decentralized approach to key distribution. Sharing of public keys or symmetric keys throughout the network is not needed. Any two routers having a primitive root a and a prime number p in common can initiate the key exchange. A simulation of the proposed approach is presented in Table 1. The basis of the proposed key exchange is discussed next.

• A.    Multi-stage Protocol

The proposed protocol is illustrated in Fig. 3. The security of the multi-stage protocol is based on the fact that a sender Alice and a receiver Bob each have their secret transformations (keys) that are only known to them, individually [11,12,13]. Routers 1(Alice) and 2 (Bob) initially share a large prime number p and its primitive root a. Knowledge of p and a by a cryptanalyst will not result in invalidating the proposed scheme. In any event, the parameters a and p are not global parameters shared among a large number of entities. They have only local significance. A few such combinations (of a and p) can be permanently embedded within router pairs. This will help them identify each other initially and thus prevent a possible man-in-the-middle attack. Once so identified, the two communicating entities can change the values of a and p at will or, if at all necessary, for example, after a major attack and/or system outage. The proposed scheme of key exchange now follows.

The key exchange initiating party, say Alice, chooses a random positive number x, where x is less than p. Alice then generates a^xmod p as the key to be shared. In other words, the key К can be represented as,

К = a^xmod p               (2)

Simultaneously, Alice chooses another random number 1 1 < p and generates an intermediate number N as,

N = a^l1mod p               (3)

Alice also computes and stores N -1 , or the inverse of N mod p. While computation of the inverse of N mod p might appear to be a formidable task, in practice, it isn’t due to the following relationships.

N^-1 = a^-4 = a^p-1-l1mod p        (4)

The latter relationship follows because for any prime number p and its primitive root alpha, we have, ap-1 = 1 mod p              (5)

Equation (3) converts the inversion process to a simple exponentiation process.

Alice preserves the key К and the intermediate numbers N = a⁴mod p and N^-1 mod p in a table.

On the first leg of transmission, Alice generates and transmits L 1 = a^x+l1 mod p . This and the subsequent transmissions are shown in Fig. 3.

Bob has similarly chosen a random number 1 2 <  p and generated the corresponding numbers a^l 2 mod p and generated its inverse a^-l 2 mod p following the procedure outlined for Alice. On the second leg from Bob to Alice, Bob generates and transmits, L 2 = a^x+l1+l 2 mod p as shown in Fig. 3.

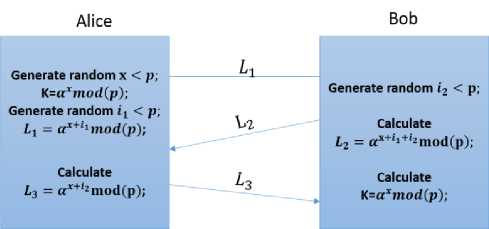
Fig. 3. Key exchange scheme using discrete logarithms

Upon receiving L 2 , Alice multiplies it by N ¹ and getting a ^-l1 mod p, thus creating,

L ₃ = a ^x+l1+l2 a ¹¹ mod p = a ^x+l2 mod p    (6)

which she then transmits to Bob on the third leg.

Upon receiving L ₃ , Bob can easily evaluate the key К as, К = L₃a^-l 2 = a^xmod(p) , which is the key Alice intended to share with Bob. Bob can similarly transmit a key to Alice.

A simulation of the values of L 1 , L 2 , and L₃ using Matlab has been done. The results for random values of 1 1 and 1 2 , a = 5,x = 15 , and p = 97 are shown in Table 1.

Table 1. Simulation of the key at Alice and Bob along with the value of each leg of the protocol

Cycle	Key At Alice's	ii	ii	Li	l2	L,	Key at Bob's
1	46	0.958478	4.238835	89.08386	52.85938	46.83984	46
2	46	4.048701	7.071245	59.04688	58	57	46
3	46	1.851114	9.189888	75.58826	6	73	46
4	46	1.737055	7.436969	31.79602	32	53	46
5	46	2.544817	9.741039	27.98389	65	89	46
6	46	2.730982	10.93591	73.00684	66	91	46
7	46	0.983038	7.114608	37.65381	31	32	46
8	46	2.436789	5.763868	52.89453	65	71.375	46
9	46	3.325503	10.80495	92.74902	45	9	46
10	46	2.784334	5.076208	61.81592	81	27.75	46

• B.    Man in the middle attack on Multi-stage Protocols

In this section, the cryptographic strength of the proposed protocol is discussed by considering its vulnerability to the man in the middle attack. It can be noted from the previous section, that the key to be transmitted is based on a random number x. This random number is never transmitted into the open nor is the actual key, which is axmod p. The transmission on the first leg L1 is ax+I1 mod. p , which is a logarithmic function of the key. An intruder having access to L1 (see Fig. 3) is handicapped because i1is an unknown quantity and even if the intruder had access to i1, the intruder will still have to compute the discrete logarithm. The same level of difficulty is associated with the intruder’s access to any of the three legs of transmission in isolation.

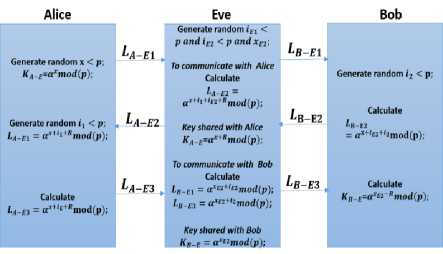
Fig. 4. Man in the middle attack on the proposed system

The case of the intruder having access to each of the three legs of transmission at the same time is considered; in other words, the intruder can access the L 1 , L₂ and L ₃ messages that belong to the same information transmission (Fig.4). It is apparent from the three equations that, after some algebraic manipulation, capture of each of these three streams will result in the intruder Eve capturing a^x mod p which is the intended key. An intruder can make use of this access by either sharing the key a^xmod p with Alice, then sharing it with Bob. Or, the intruder can effect a man in the middle attack where he/she shares a key with Alice (K_AE) and another key with Bob ( K_{B E}) . This case is shown in Fig.4, and a simulation of the results L_{A E1} , L_A _ _E2 , and L_A _ _E3 (transmissions between Alice and Eve), L_{B E1}, L_{B E2}, and L_{B E} 3 (transmissions between Bob and Eve), using Matlab has been done. The results for random values of i 1 , i₂ , i _E1 , and i_E2 with a = 5, x = 15, x_E2 = 20, and p = 97 have been presented. As seen from Table 2, a secret key will be shared between Alice and Eve and a

Table 2. Simulation of a successful man in the middle attack in case of a multi-stage protocol without an initialization vector

Cycle Key shared between Alice and Eve Lai La2 Ьаз Lbi Lb2 Ьвз Key shared between Eve and Bob 1 46 40.56 44.5 79.70 18 69 50 93 2 46 8.32 39 30 60 34 72 93 3 46 68.18 65 56 29 38 42 93 4 46 40.31 37 33.62 87 96 44 93 5 46 23.75 87.12 10.65 5 88 40 93 different secret key will be shared between Eve and Bob. During the communication Alice and Bob will not be able to detect the presence of Eve in the middle.

These vulnerabilities are effectively addressed in the proposed protocol in the next section.

• IV.    P roposed P rotocol U sing A n I nitialization V ector A nd I ts C ryptographic S trength

One can think of numerous ways to deny Eve from simultaneously accessing all of the three legs of the transmission. An obvious way is to send the information on each of the three legs on separate fibers or separate DWDM channels of one fiber. Furthermore, such assignments can be randomized.

Another way to frustrate Eve from accessing the key even after a successful capture of the three messages is to retain a subset of the last interchange of the key between Alice and Bob, and couple it with the new key a^xmod p to be transmitted with the following transformation, a^xa^Rmod p, where a^R represents a remnant of the key successfully transferred during the last interchange. Since only Bob has access to R, he can easily derive the key a ^x mod(p). In addition to providing security, use of the remnant R will also obviate any man-in-the-middle attack. It should be noted that since R is changing periodically, it is substantively different from the Initialization Vector used in conventional cryptography where it is fixed and therefore subject to a range of cryptanalytic attacks. The proposed approach is discussed in detail in the following section.

• A.    Description

As indicated in Section IV, the problem with the multistage algorithm is that if an intruder is present on all the stages of the communication at a given time, he/she will be able to get the ciphertext at each stage of the protocol [14]. Knowing the cipher text at each stage of the protocol, the intruder will be able to solve the following system of simultaneous equations:

L 1 = a^x+l1 mod p = m (7)

L₂ = a^x+l1+l 2 mod p = m' (8)

L ₃ = a ^x+I2 mod p = m" (9)

where m, m', and m'' are the values measured at L 1 , L ₂ , and L₃ respectively. An underlying assumption, of course, is that a and p are known.

Since these are not global parameters, in the absence of inside information, Eve will be locked out from getting the key. In the following we address the situation when these parameters are available to the intruder and show how the use of the initialization vector will still prevent Eve from accessing the key.

In the previous section, we proposed a way to prevent such type of attacks by using a remnant from a previously used key aR. Thus the number of stages of the protocol are only three, while the number of random variables used to protect the message are four. On the first leg of transmission, Alice generates and transmits L1 = aRl1 mod p. On the second leg from Bob to Alice, Bob generates and transmits, L2 = aR(l1+l2) mod p . Upon receiving L2, Alice creates L3 = aR(x+l2) mod p which she then transmits to Bob on the third leg. Bob has a prior knowledge of both R and 12 thus he can recover the key sent over the channel.

Thus the set of equations that should be solved by an intruder tapping the channel can be presented as follows:

L1 = aRl1 mod p = m

L2 = aR(Ii+I2) mod p = m'

L3 = aR(l2+x) mod p = m''

Since it’s impossible to solve for four unknown variables with only three equations, the key exchange is secure.

• B.    Mode Of Operation

We call R ₀ [n] the initialization vector at iteration 0, cycle number n, x₀ [n] the bit value of the message being transferred, and i ° [n] and i ° [n] the values of the transformations (keys) at iteration 0, cycle number n, associated with the sender (Alice, 1) and receiver (Bob, 2), respectively. The initial length of R _o is denoted by z, thus after z cycles R _o will be updated to a new string of values R 1 of the same length as R _o .

At iteration 0, cycle number n, the messages transmitted at L₁₀, L 2 0 , and L₃₀ respectively are:

L1,o = aR°[n] l°[n] mod p(13)

L2,o = aR°[n](l°[n]+l°[n]) mod p(14)

L3,0 = aR°[n](x°[n]+l°[n]) mod p(15)

It should be noted that the key to be transmitted K ₀ [n] = a ^x°[^n] mod p has been used only in the last leg. This approach can also be used in the set of equations where the initialization vector R _o was not used. Potentially, this is an additional deterrent to a cryptanalyst.

At the next cycle, Alice will use a new transformation set 1 0 [n + 1] and Bob should use 1 0 [n + 1] and a next value in the string of the initialization vector R _o [n + 1] will be used. It is worth noting that Alice and Bob do not have any restrictions on the transformations associated with R, and it does not need to commute with i 0 [n + 1] and i 0 [n + 1]. Furthermore, it is worth noting that Alice and Bob can use the bits of R in any desired order as long as there has been a previous agreement on the way of using them. The operation of the proposed approach is depicted in Fig. 5. A simulation of the proposed approach is presented in Table 3 for random 1 1 , 1 2 , and x, with a = 5, x_E2 = 20, and p = 97.

Table 3. Simulation of the operation of the multi-stage protocol using an initialization vector R

	Cycle	Key at Alice	<1     <2    ^10    ^20    ^3,0					Key at Bob	Ro
2	1	14.28	2.41	5.75	45.32	70.91	32.92	14.28	4.71
	2	49.32	1.33	10.63	52.34	30	89	49.32	9.89
	3	24.55	2.87	10.05	41.5	8	33	24.55	29.95
	4	14.72	3.34	1.48	11.66	76.61	11.21	14.72	25.80
	5	62.82	4.07	3.49	39.42	37	87.11	62.82	27.50
	Cycle	Key at	4	4	£11	^2.1	^-3,1	Key at Bob	«1
	1	69.92	3.19	4.91	65.59	67.31	94.26	69.92	64.94
	2	81.19	0.65	3.44	71.17	80.92	80.06	81.19	22.4
	3	27	4.66	6.16	42.20	40	69.78	27	207.9
	4	61.69	3.92	9.95	38.27	58	35	61.69	46.27
	5	88.65	2.95	8.82	78.46	78	41.18	88.65	8.44

After the addition of an extra dimension to the multistage protocol proposed in the previous section it is possible to consider it as a continuously refreshing key since, at each stage of the protocol, a new secret variable is added in order to secure the outcome of the previous stage. An eavesdropper having simultaneous access to the three stages of the protocol will not be able to compute the value of the sent bit, since he/she will be faced with the problem of solving a system of three equations with four variables. In addition, such an approach makes it impossible to launch a man in the middle attack.

The addition of an initialization vector to the three-stage protocol can be regarded as a door function to protect the message sent over the channel. Any illegitimate user is denied the ability of retrieving the value of the bit sent over the channel as long as he/she does not possess the value of the door function.

• C.    A Two-Stage Protocol

The protocol proposed in Section IV.B can be further reduced into a two-stage protocol if one allows the communication to start at Bob’s side and end at Bob’s side as well (shown in Fig. 6). The protocol proceeds as follows: Alice and Bob initially share a large prime number p and its primitive root a and an initialization vector R of length z to proceed with the first iteration of the protocol. Knowledge of p and a by a cryptanalyst will not result in invalidating the proposed scheme, while R is only known to Alice and Bob as a remnant from a previous exchange. In any event, the parameters a , p , and R are not global parameters shared among a large number of entities. They have only local significance. As before, a few such combinations (of a and p) can be permanently embedded within router pairs. The key exchanging party, say Alice, chooses a random positive number x, where x is less than p. Alice then generates a ^ mod p as the key to be shared. In other words, as stated earlier, the key К

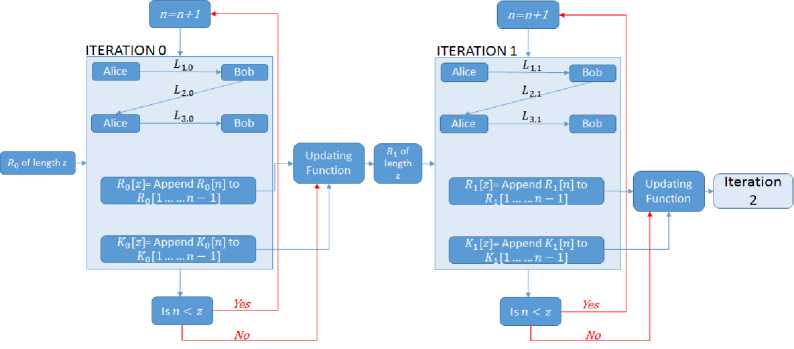
Fig. 5. The operation of the multi-stage protocol using four variables

can be represented as,

К = a^xmod p            (16)

As discussed before, the key at the first iteration is denoted by К[п]₀ = а^^{1 1}] mod p . Bob starts the communication by sending L 1 = a^Rl 2 mod p, where i₂ a random integer and is known only to Bob. Upon receiving the message, Alice encodes a^xmod p , which is the key to be transmitted, and protects the message using the initialization vector R , and sends L 2 = ^ вСж+гг) mod p to Bob. Bob receives the message his prior knowledge of R and i₂ gives him the ability to decode the message sent from Alice.

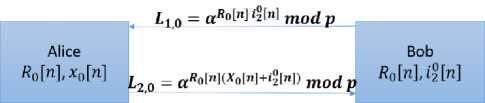
Fig. 6. Key exchange scheme using the two-stage protocol (iteration zero cycle n)

The initialization vector R is updated periodically to insure a fully secure information transfer between Alice and Bob.

R ₀ [n] is the initialization vector at iteration 0 cycle number n, x ₀ [n] the bit value of the message being transferred, i 0 [n] the values of the transformations (keys) at iteration 0 cycle number n of the receiver (Bob). The initial length of R ₀ is denoted by z, thus after z cycles R ₀ will be updated to a new string of values R 1 , of the same length.

At iteration 0 cycle number n the messages transmitted at L₁₀, and L 2, ₀ are:

L^ 0 = a ^R°^[n] ^^ mod p          (17)

L 2,₀ = а ^к°[^п](х°[^п]+1°[^п]) mod p         (18)

At the next cycle Bob will use i 0 [n + 1] and the next value in the string of the initialization vector R ₀ [n + 1] will be used. It is worth noting that Alice and Bob do not have any restrictions on the transformations associated with R , it can be an addition to the exponent, a multiplication or any other mathematical transformation.

At the end of each iteration an updating function having its inputs as the randomly generated key К and the initialization vector R is used to generate a new initialization vector to be used in the next iteration. As shown in Fig.7, R ₀ is used to generate the key at iteration 0. Then, using R ₀ and К 0 the updating function generates a new initialization vector R 1 of length z to be used for iteration 1.

• D.    Braiding Concept

The concept of using different versions of the multistage protocol in the same communication called the braiding function was introduced in [15], and is shown in Fig. 8. Braiding is the concept of sharing keys between two parties using different number of stages, m. Alice and Bob can agree on how many stages to use at the onset of the key distribution process. The variability associated with m (which can be changed at will by the communicating parties) will be an additional means of frustrating the eavesdropper Eve.

In Fig. 8, the braiding concept of multi-stage protocols is shown. Given an initialization vector R ₀ of length z Alice and Bob execute a multi-stage protocol with m=3 for z cycles. Then after sharing a key К 0 of length z, the initialization vector R ₀ is updated into R 1 using an updating function. The new initialization vector R 1 is based on both К 0 and R ₀ . R 1 is now used to do the next iteration of the key distribution process. At this iteration Alice and Bob use m = 2 to share К 1 .

• E.    Man In The Middle Attack On A Multi-Stage Protocol Using An Initialization Vector

In this section, we show that a multi-stage protocol

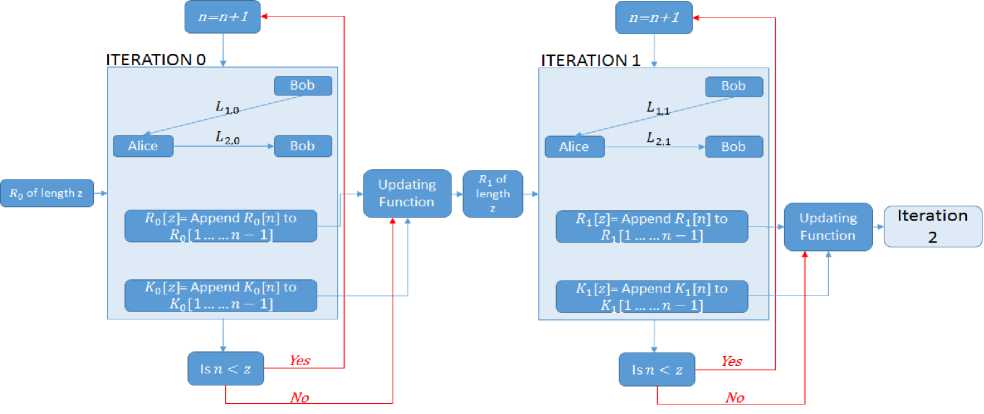
Fig. 7. The operation of the multi-stage protocol using three variables

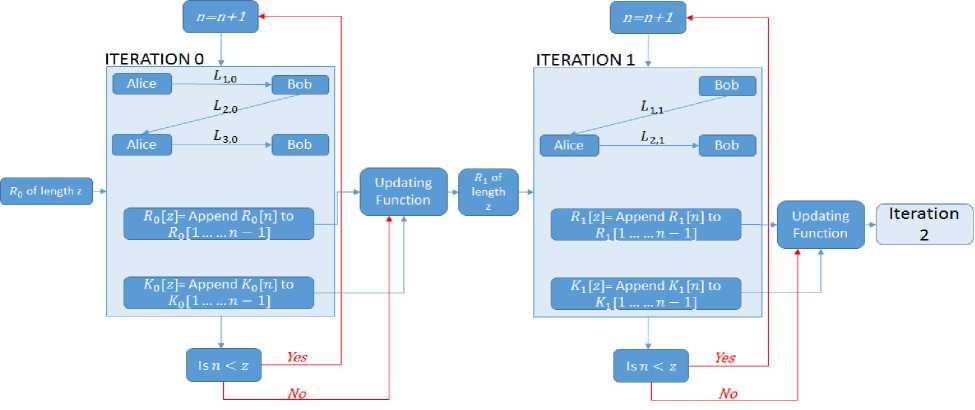
Fig. 8. The operation of the braided multi-stage protocol

Alice                        Eve                         Bob

	^A-El	Generate random iE1<  p and iE2 < p and xE2;	^B-El	Generate random i2 < p; Calculate
Generate random x < p; KA_E-ctxTnod(p); Generate random iA < p; LA_E1 = aRllmod(py Calculate LA_E3 = a^+^modfp);	Ьд—Е2	To communicate with Alice Calculate LA_E2 = aR11+1£2mod(p); Key shared with Alice	^B-E2
	_^а-ез	KA_E=ctRxmod(p); To communicate with Bob Calculate Lb_e1 = alE2mod(p); Lb_E3 = aXE2+Rl2mod(p); Key shared with Bob KB_E = aXE2mod(py,	^B-E3	^b-E2 = ctlE2+Rl2mod(p); Calculate KB_E=aXE^Rmod(p);

Fig. 9. Man in the middle attack on the Multi-stage using an Initialization Vector using an initialization vector is not vulnerable to the man in the man in the middle attack. The man in the middle attack stage protocol is shown in Fig. 9. Table 4 shows the keys at Alice, Bob and Eve for i1, i2 , iE1, and iE2 with a = 5,x = 15 , xE2 = 20 , and p = 97 , the simulation presented in this table. As shown from the table the key at Alice is different than the key that Eve will attempt to use while communicating with Alice (shown in blue). The same case applies to Eve and Bob as well (shown in red). This is due to the initialization R0 vector used by Alice and Bob.

Table 4. Man in the middle attack to a multi-stage protocol using an initialization vector

Cycle	Key at		La		Key	Key Bob				Key at Bob
1	46	44.42	93	61	63.12	61	42	93	86.87	93
2	46	36.50	5	37	75.29	80.62	33	68	70	93
3	46	15.78	33	61	50.01	45.75	46	34	91	93
4	46	81.95	16	52.24	33.19	60.34	36	46	46	93
5	46	69.21	26	54	4.04	33.81	35	8	22	93

• F.    Characteristics of the Proposed Protocol

The protocol proposed in this paper is a multi-stage ultra-secure router-to-router spontaneous key exchange system. This protocol represents a decentralized approach to conventional key distribution schemes and is meant for use on a link-by-link basis between two communicating parties. In other words, the overhead of sharing public keys throughout the network is obviated as well as the need of a third party to distribute secret keys between the nodes of the network.

The proposed protocol is based on the usage of random number generators. Two random number generators at both Alice’s and Bob’s side are needed to generate i 1 and i ₂ , respectively. Furthermore, the security of the proposed approach against a man in the middle attach is guaranteed as long as an initialization vector is already in the possession of the communicating parties at the time communication first starts. This initialization vector can be embedded in each of the two communicating router pairs by the manufacturer, and then updated as often as chosen by the communicating routers.

Finally, the multi-stage protocol requires several transmissions on the channel depending on the number of stages m agreed on between Alice and Bob. Such requirement can be considered as an additional strength associated with the protocol, since, in a braided scheme, it can frustrate an eavesdropper who is unaware of the value of m.

• V.    C omparison with QKD S ystems

Quantum key distribution systems are commercially available from at least two suppliers: MagiQ Systems [16] and IdQuantique [17], based in Boston, MA in the US, and in Geneva, Switzerland, respectively. Both these manufacturers use the BB’84 protocol [18], first discovered in 1984, and first manufactured for commercial applications in 2005. Currently available QKD equipment are based on single photons each carrying one bit of information. Since it’s impossible to generate single photons with defined periodicity [19], a practical way to closely approach it is by way of reducing the beam strength to such a low value that photons are generated very sparsely and the corresponding probability of having two or more photons in a single time slot is arbitrarily small. This, of course, creates two problems. The rate at which information can be transmitted is relatively modest to the tune of a few kilobits per second. Furthermore, since the carrier is a single photon, the distance over which it can be detected with integrity is limited to about 100 km in an optical fiber. Additionally, other environmental restrictions also limit its use to all but a few commercial applications. It’s unlikely that the currently available QKD techniques will notice an observable spike in their applicability space.

In comparison, the proposed system is based on a classical method of encryption and does not require a quantum channel. The key distribution can take place over the same medium that carries the payload and the speed of transmission is the same as that of the payload. There are no restrictions on the intervening medium of any kind. Even if the two routers were not directly connected or even with the intervening medium consisting of different technologies in tandem, e.g., EPON, DWDM, Wireless, etc., the process described does not change. Very importantly, the key exchange can take place as often as desired making the proposed system offer security comparable to quantum key distribution techniques.

• VI.    C onclusions and F uture W ork

This paper has presented an ultra-secure router-to-router key exchange system using multi-stage protocols. The key exchange process can be initiated by either party at will and can be carried out as often as necessary. The proposed system is based on the use of discrete logarithms. The main cryptographic strength of the proposed protocols lies in the use of multi-stage transmission where the number of variables exceeds the number of stages by one, ensuring that the number of possible measurements is one less that the number of variables. This makes the key transfer secure. Furthermore, since the keys can be exchanged as often as necessary at the payload speed, one can stipulate that the security of the proposed system approaches that of contemporary QKD systems. In other words, the level of security attainable by the proposed system is comparable to QKD systems but without the baggage of limited distance and low speed associated with the latter. Recent literature in quantum-secure communication in a multi photon environment [12-15] has suggested that the multiphoton approach can offer quantum level security obviating the need for single photon generators and thus removing the speed and distance barrier caused by single photons. This paper has shown that a cryptographic strength similar to the multi-photon approach is attainable in electronics as well.

The proposed technique has used discrete algorithms as the base for secure communication. Another possible technique can be based on the use of elliptic curve cryptography [18] while augmenting it with the use of a similar multi-stage protocol. The latter technique will offer a comparable cryptographic strength.

A cknowledgment

This research was supported in part by the National Science Foundation (NSF) under Grant 1117179.