Аналитическая модель арочного эластомерного амортизатора для применения в имитационном моделировании систем

Арочные эластомерные амортизаторы применяются для защиты различной аппаратуры и оборудования от ударов и обладают сложными нелинейными силовыми характеристиками. Для имитационного моделирования систем на базе арочных эластомерных амортизаторов для последних важно разработать аналитическую математическую модель, по возможности зависящую от минимального числа параметров. Одна из таких аналитических моделей рассмотрена в [1].

Целью работы является разработка аналитической математической модели определения зависимости реакций арочного эластомерного амортизатора от деформаций, предназначенной для использования в имитационном моделировании систем амортизации. Здесь и ниже реакциями амортизатора будем называть усилия, действующие со стороны амортизатора на установленный на нем

объект и вызванные взаимным смещением объекта и основания (по оси амортизатора и в поперечном направлении). Аналогично ниже будем говорить о реакции каждой из двух эластомерных стенок, из которых складывается реакция амортизатора.

Для составления математической модели достаточно знать силовую статическую характеристику при работе амортизатора на сжатие, геометрические размеры и свойства материала. Такой подход оправдан в виду того, что в литературе, как правило, приводятся характеристики арочных амортизаторов только на сжатие [2; 3]. Подобная модель позволит оценить работу амортизатора и в поперечном направлении. Поперечную силовую характеристику необходимо учитывать при сложном нагружении, в т. ч. когда амортизаторы установлены под углом.

1.    Общие положения

Общий вид амортизатора, для которого строится математическая модель, с его упругой силовой характеристикой на сжатие представлен

Том 6

на рис. 1. Под упругой силовой характеристикой понимается зависимость усилия амортизатора от абсолютной деформации в определенном направлении при медленном изменении нагрузки (без учета демпфирования). Деформация задается перемещением верхней пластины (поз. 1 на рис. 1). Нижняя пластина (поз. 3 на рис. 1) считается жестко закрепленной.

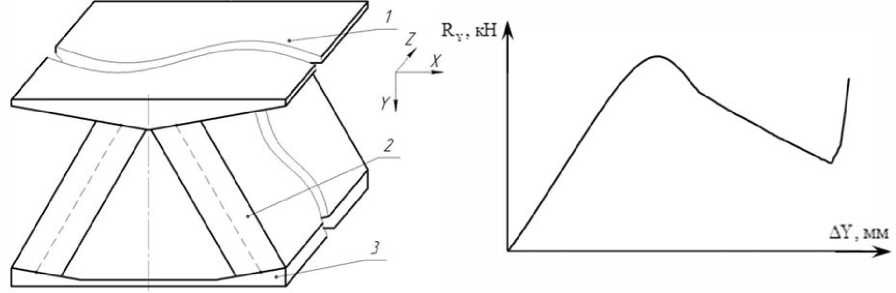
Рис. 1. Общий вид арочного эластомерного амортизатора и его силовой характеристики на сжатие: 1 ‒ верхняя металлическая пластина; 2 ‒ эластомерная стенка; 3 ‒ нижняя металлическая пластина

Предлагается математическая модель, в которой усилие арочного эластомерного амортизатора представляется как совокупность усилий двух его независимых эластомерных стенок 2. Математическая модель строится в предположении, что реакция амортизатора в основном создается проекциями усилия сжатия (растяжения) каждой стенки на вертикальное и боковое направление. Дополнительно учитывается жесткость эластомерных стенок на сдвиг и изгиб. В данной математической модели для описания работы амортизатора достаточно знать только одну его упругую (статическую) силовую характеристику на сжатие и геометрические размеры. По известной упругой силовой характеристике сжатия амортизатора определяется упругая силовая характеристика одной стенки. Упругую силовую характеристику амортизатора на сжатие можно получить моделированием методом конечных элементов, как, например, в работе [1], либо по результатам испытаний (такие данные приводятся в литературе, например [2]). В настоящей статье за основу берется силовая характеристика, полученная в пакете конечно-элементного анализа Ansys Workbench 18.1.

2.    Математическая модель

При разработке математической модели принимается, что вертикальная реакция R_Y вдоль оси Y считается положительной, если амортизатор сжат. Ось Y направлена вниз. Продольная реакция R ⁿ одной стенки также положительна при ее сжатии. Расчетная схема представлена на рис. 2.

Считается, что эластомерные стенки жестко заделаны в металлические пластины. На рис. 2 точка А ‒ точка пересечения средней линии эластомерной стенки с верхней пластиной ( А ₀ ‒ начальное положение), точка В ‒ точка пересечения средней линии эластомерной стенки с нижней пластиной. Точка В , как и нижняя пластина, неподвижна. Реакция одной стенки раскладывается на продольную составляющую R ⁿ , направленную по оси n вдоль средней линии в точке А , и перпендикулярную ей тангенциальную составляющую R ^τ , направленную вдоль оси τ. Так как концы стенок в местах заделки не поворачиваются, то ось n имеет постоянный угол наклона в процессе нагружения амортизатора, равный наклону α_ст эластомерной стенки к оси х недеформированного амортизатора.

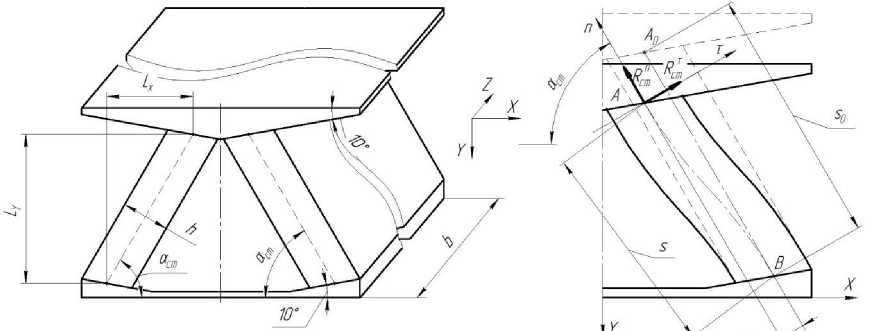
Рис. 2. Расчетная схема для определения реакций

Продольная составляющая R ⁿ реакции амортизатора зависит от изменения длины ∆ s эластомерной стенки. В начальном положении длина стенки s ₀ равна:

^ o = A o B = ^L + L, , (1) где L_x и L_y – разности координат точек А ₀ и В нена-груженного амортизатора.

В деформированном состоянии средняя линия стенки в общем случае имеет криволинейную форму. Приближенно длина средней линии принимается равной расстоянию между точками А и В . Тогда изменение длины ∆ s при плоском нагружении амортизатора составит:

^ S i = J L x + L - 7 ( L x ±A x )² + ( L y -A y )², (2) где ∆ x и ∆ y – проекции смещения точки А относительно начального положения А ₀, равные перемещению верхней пластины вдоль осей x и y . Здесь и ниже i = 1 относится к левой стенке (рис. 2), i = 2 ‒ к правой стенке. На рис. 2 показана схема деформации правой стенки. Система координат n –τ левой стенки симметрична относительно плоскости симметрии амортизатора.

Смещение ∆τ определяется выражением:

рис. 2, значительно больше толщины h и обычно больше длины s ₀, в (7) целесообразно заменить жесткость стержня E ∙ J^z на произведение цилиндрической жесткости пластины D на размер b :

kи

12 • D • b

s03

.

Цилиндрическая жесткость D пластины

определяется формулой [6]:

D=

E • h3 12 • (1 — v2),

где h ‒ толщина стенки, v ‒ коэффициент Пуассона материала.

Сложнее определить продольную силовую упругую характеристику одной стенки – зависимость R n = R n ( А,Ат). Отметим, что данная характеристика является существенно нелинейной ввиду потери устойчивости стенки, причем критическое усилие, соответствующее потере устойчивости, зависит как от продольных, так и от тангенциальных деформаций.

Силовая характеристика стенки заранее обычно не задана, но она однозначно связана с характеристикой сжатия амортизатора. При этом

Δτ = Δ x ⋅ sin α _ст -Δ y ⋅ cos α _ст .         (3)

Составляющая реакции R ^τ , направленная вдоль оси τ, зависит от смещения ∆τ и определяется выражением:

Rсτт =-k⋅Δτi,                 (4)

следует учитывать, что модуль сдвига связан с модулем упругости через коэффициент Пуассона [7], который для эластомерных материалов близок к 0,5 (несжимаемый материал) [8].

При чисто вертикальном сжатии (∆ x = 0) продольная реакция одной стенки равна:

где k ‒ жесткость одной эластомерной стенки амортизатора в направлении оси τ, определяемая как жесткость последовательно соединенных элементов, работающих на сдвиг k ^с и изгиб k ^и:

R em ^x =0 = ^R cm (^ ^ A x =0 , ^^T A x =0 ),         ⁽¹⁰⁾

кс • к и кс+ки.

Коэффициент жесткости стенки на сдвиг k ^с определяется выражением [4]:

где ∆ s _{∆ x =0} и ∆τ_{∆ x =0} определяются в зависимости от вертикального сжатия амортизатора ∆ y по формулам (2) и (3) соответственно при ∆ x = 0.

Зависимость реакции стенки R _c n _T ^x=0 от A y строится из известной зависимости R_Y (∆ y ) для вертикальной реакции амортизатора в целом при ∆ x = 0 следующим образом. Имеем:

к с =

G ■ F

so   ,

Ry (Ay) = 2 • Rn A,=0 • sin а ст + +2 • RL (AtAx=0 ) • cos аст.

где G ‒ модуль сдвига, F ‒ площадь поперечного сечения стенки.

Коэффициент жесткости стенки на изгиб k ^и может быть определен из выражения для прогиба балки, защемленной по концам от поворота [5]:

С учетом (3) и (4) получим:

n

R ст Δ x = 0

R (∆y) -2⋅k⋅∆y⋅cos2 α 2⋅sinαст

kи

12 • E • Jz

s

Проводя расчеты для разных ∆ y , строим табличную зависимость R ⁿ от ∆ y и ∆ s от ∆ y . Учитывая, что при ∆ x = 0 значения ∆ y , ∆ s и ∆τ однозначно связаны друг с другом, табличным значениям ∆ s ставятся в соответствие табличные

где E ‒ модуль упругости, J^z ‒ момент инерции прямоугольного сечения относительно оси, перпендикулярной плоскости рис. 2, и пересекающей нейтральную ось стенки.

Учитывая, что ширина b эластомерной стенки вдоль оси z , перпендикулярной плоскости

значения R ⁿ . Полученную таким образом табличную зависимость назовем базовой и обозначим Т? е _тБ (A s ). Промежуточные значения определяются линейным интерполированием.

Отметим, что при отсутствии данных о модуле упругости E и модуле сдвига G для эласто-

Том 6

мерного материала, из которого выполнен амортизатор, эти значения можно оценить по уже известной упругой силовой характеристике стенки амортизатора на сжатие при малых смещениях, когда эффектами изменения формы и потери устойчивости можно пренебречь. В случае, если модули упругости и сдвига неизвестны, задача решается итерационно. В первом приближении характеристика строится без учета тангенциальной составляющей, т. е. при k = 0. Модуль упругости Е оценивается по условию [6]:

^ (0) = E •F . 6(Ns)V ’   (1 -v2) • sо

Далее по модулю упругости Е определяется модуль сдвига G . После этого по формулам (5–7) вычисляется k в первом приближении, снова стро^{ится R}n Ax =0 ^{( A} y ) и т д.

При анализе работы стенки на сжатие одним из определяющих является значение критической силы, при достижении которой стенка теряет устойчивость. У эластомерной стенки амортизатора, показанного на рис. 1, края, которыми она крепится к пластинам, защемлены, а два других края свободны. Поэтому эластомерная стенка представляется как балка с двумя заделанными от поворота концами. Как показывают исследования, представленные в [9], представление пластины как стержня с тонким сечением для определения критического усилия потери устойчивости дает приемлемый для практических расчетов результат. Кроме того, определение критического усилия по методикам [10–12] для прямоугольных пластинок затрудняется ввиду того, что эти методики, в основном, ориентированы, во-первых, на пластинки с опертыми и/или защемленными тремя-четырьмя краями, а во-вторых, на пластинки с соотношением высоты s ₀ к ширине b более 1, в то время как у эластомерных стенок рассматриваемого в настоящей работе амортизатора это соотношение значительно меньше 1 (широкие пластинки). Необходимо отметить, что для других типов арочных эластомерных амортизаторов с иным креплением стенок и соотношением сторон возможно более приемлемым будет определение критического усилия потери устойчивости именно по методикам для плоских пластин.

При ∆τ = 0 балка центрально сжата, а критическая сила, при которой балка теряет устойчивость, определяется по формуле Эйлера [13] с заменой в ней жесткости стержня E ∙ J^z на произведение D ∙ b :

можно определить как абсциссу точки на продолжении участка характеристики R " _Б (A) до потери устойчивости с ординатой P _кр (рис. 3).

Однако, ввиду того, что эластомерные стенки амортизатора находятся под углом к вертикальной оси Y , при вертикальном сжатии амортизатора (в т. ч. при определении базовой характеристики R " б (A)) эластомерная стенка находится в сжатоизогнутом состоянии. У стержней изгиб снижает значение критической силы, соответствующей потере устойчивости по сравнению с центрально нагруженными [10]. Следовательно, при определении критического усилия, при котором стенка при вертикальном сжатии амортизатора теряет устойчивость, следует учитывать влияние тангенциальных смещений ∆τ (рис. 2). При чисто вертикальном сжатии (∆ x = 0) из (3) следует:

Δτi = -Δy cos αст.

Наличие таких деформаций приводит к тому, что сила, при которой стенка теряет устойчивость, существенно ниже эйлеровой.

С учетом вышесказанного общее выражение для продольной составляющей реакции стенки R n = R n (А, Ат) должно одновременно удовлетворять условию R n д ₌₀ = R n ⁽ А _{Х ; =0} , Ад ₌₀) ⁽т. е. базовой характеристике R-- _б (A s )) и описывать потерю устойчивости при ∆τ = 0 и ∆ s = ∆ s _кр. Искомую зависимость предлагается представить в виде:

R n (A s ,Ат) = R ^ (A s ) + R n _п (A s , Ат), (15) где R- _п (-A s , Ат) - корректирующая поправка, которая учитывает изменение критической силы относительно базовой характеристики R" n _Б (A s ).

С учетом (15) продольную реакцию Rn = R (А, Ат) каждой стенки предлагается определить выражением:

RCmi= R СТб (А^) + ( Ркр - R Ст Б (А^) )■

■(а■ 10 0,3'Ат'I + в)■ exp

Г -(Asi—Asкр )2 )

I     2 ■°2     J

s

i где а и в - параметры; о5 = бБ- - параметр ширины области корректировки усилия по сжатию стенки, h i =      ‒ радиус инерции сечения стенки. Без- z 12

размерное тангенциальное смещение Δ τ в формуле (16) определяется выражением:

Δτi =

P кр

п2 • D • b (Ц- 50)2 ,

s02 ⋅ Δτi h3

где μ – коэффициент способа закрепления (μ = 0,5).

Отметим, что потере устойчивости соответствует изменение длины стенки ∆ s _кр, которое

Первое слагаемое в (16) ‒ базовая характеристика R-- - (A s ) . Она характеризует изменение продольной реакции стенки при вертикальном сжатии амортизатора. Второе слагаемое – поправка, которая учитывает изменение критической силы в за-

висимости от ∆τi. Первый множитель представляет собой разницу между критическим усилием Ркр, определяемым по формуле (14), и усилием по характеристике R^ Б (Av) в рассматриваемой точке. Для того чтобы прибавка увеличивалась по мере уменьшения по модулю ∆τ применяется второй множитель, максимальное значение которого равно 1 и достигается при ∆τ = 0. Однако, ∆τ может оказаться близким к 0 при различных величинах ∆s, в том числе когда потери устойчивости не происходит (например, поперечное смещение амортизатора при малом сжатии). Для учета увеличения корректирующей прибавки усилия в области потери устойчивости стенки применяется экспонента, максимальное значение которой также равно 1. В связи с этим, максимальное значение реакций R n при сжатии эластомерной стенки не превышает критическую силу Ркр и равно последней только при одновременном выполнении условия ∆τi = 0 и ∆si = ∆sкр.

Параметры α и β находятся по ∆τ( x ; y ) из условий:

а.10-0,3М+р = 1, Ат, = 0а.10-0,3М+р = о, Лт" = Лт"  ,

~      ,      i          i кр

где Δτ ‒ определяется по (17) при ∆τ _i = –∆ y _кр∙cosα_ст. В свою очередь, ∆ y _кр определяется как значение вертикального сжатия амортизатора, соответствующее максимуму характеристики R_Y (∆ y ) (рис. 3).

Демпфирующая составляющая реакции амортизатора выражается формулой [14]:

R Д =- Сх ' Vx

Д

Y     ^Су  ^VY ,

где v_X и v_Y ‒ скорость верхней пластины относительно нижней вдоль соответствующих осей, c_X и c_Y ‒ коэффициенты демпфирования.

Коэффициенты демпфирования для эластомерных амортизаторов можно определить, зная коэффициент потерь ψ [15; 16].

Усилие амортизатора вдоль оси Y (нормальное) и оси Х (поперечное) определятся выражениями:

RY = (RCT1 + Rn2 ) • sin «ст + +(RCT1 + Rст2 ) • cos аст + RY1, RX = (RCT1 — Rn2 ) • cos аст +

+(-RCTi + RCT2) •sin аст + RX.

Таким образом, по одной заранее известной силовой характеристике сжатия всего амортизатора строится силовая характеристика одной эластомерной стенки, посредством которой, в свою очередь, определяется реакция амортизатора как в вертикальном, так и в боковом направлениях.

• 3.    Результаты расчетов

В настоящем разделе представлены результаты расчетов реакций арочного эластомерного амортизатора, размеры и параметры которого приведены в табл.

Таблица

Параметры амортизатора

Параметр	Значение
LX , м	0,118
LY , м	0,068
Е , Па	6,52∙106
G , Па	2,18∙106
h , м	0,038
b , м	0,48
s 0, м	0,136
αст, град	80
P кр , Н	4∙104
σ s , м	5∙10-3
∆ s кр , м	0,031
α	1,0208
β	0,0208
∆ y кр , м	0,034

Графики зависимости упругой характеристики амортизатора R_Y (∆ y ) и базовой характеристики продольной реакции одной стенки R ^ б (^) представлены на рис. 3.

На рис. 4‒7 представлены графики упругих реакций амортизатора без учета демпфирования вдоль осей Х и Y , полученные по предлагаемой модели и в пакете конечно-элементного анализа Ansys Workbench 18.1. Расчеты проводились в соответствии с положениями раздела 1 и 2. Расчет зависимостей поперечной реакции R_X (∆ x ) вдоль оси Х и вертикальной R_Y (∆ x ) вдоль оси Y от поперечного перемещения ∆ х проводился при разных величинах поджатия амортизатора ∆ y . Расчет зависимости R_Y (∆ y ) проводился при разных величинах поперечного смещения ∆ х .

Как видно из графиков увеличение поджатия ∆ y до 40 мм приводит к существенному расхождению зависимостей поперечной реакции R_X (∆ x ), полученной по аналитической модели и в пакете конечно-элементного анализа, в частности, к изменению знака, т. е. направлению действия реакции. Это связано с тем, что при больших величинах сжатия ∆ y амортизатора поперечное смещение вызывает соприкосновение изогнутой эластомерной стенки с пластинами или даже самосмыкание, в результате чего возникает быстрое возрастание усилия. По сути, это является пробоем амортизатора [15]. По этой же причине с увеличением поперечного смещения ∆ х снижается вертикаль-

(омчесЬё

АППАРАТЫ И

Том 6

чей области достигается приемлемое для практических расчетов схождение результатов расчетов усилий, полученных по аналитической модели и в пакете конечно-элементного анализа Ansys.

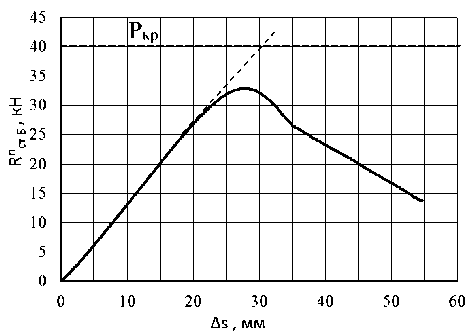
Рис. 3. Графики зависимостей упругих характеристик амортизатора R_Y (∆ y )

(сплошная линия) и одной стенки R n _Б (A ) (пунктирная линия)

ный ход амортизатора ∆ y до возникновения пробоя. В большинстве случаев работа амортизатора в условиях пробоев при защите амортизируемого объекта является недопустимой. В пределах рабо-

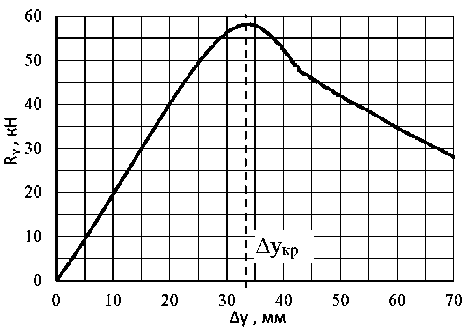
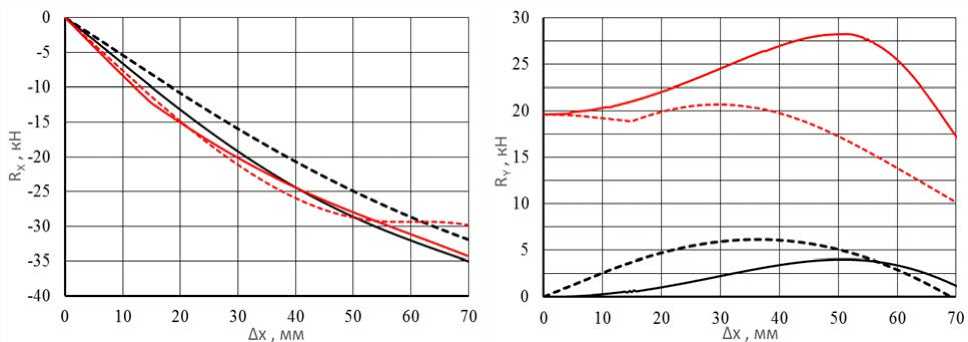
Рис. 4. Зависимость реакций R_X (∆ x ) и R_Y (∆ x ): сплошные линии ‒ в пакете Ansys ; пунктирные линии ‒ по аналитической модели; черный цвет ‒ реакции при поджатии ∆ y = 0 мм; красный цвет ‒ реакции при поджатии ∆ y = 10 мм

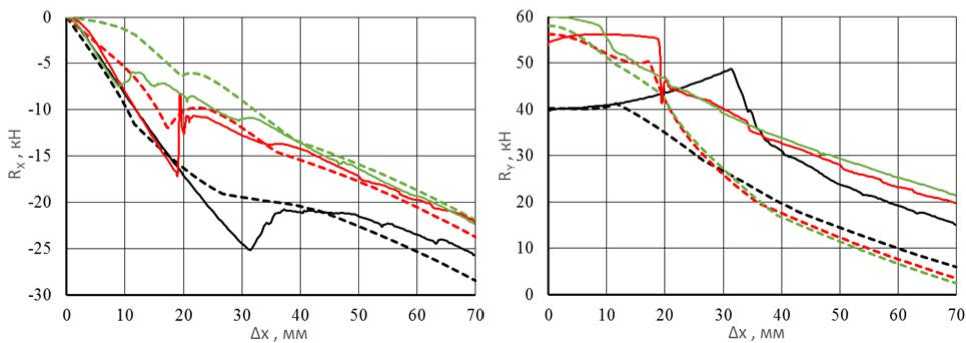
Рис. 5. Зависимость реакций R_X (∆x) и R_Y (∆ x ): сплошные линии ‒ в пакете Ansys ; пунктирные линии ‒ по аналитической модели; черный цвет ‒ реакции при поджатии ∆ y = 20 мм; красный цвет ‒ при поджатии ∆ y = 30 мм;

зеленый цвет ‒ при поджатии ∆ y = 35 мм

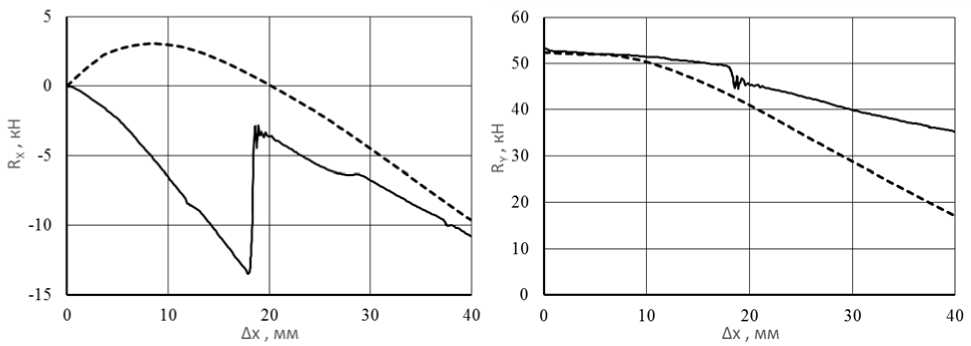
Рис. 6. Зависимость реакций R_X (∆ x ) и R_Y (∆ x ) при поджатии ∆ y = 40 мм: сплошные линии ‒ в пакете Ansys ; пунктирные линии ‒ по аналитической модели

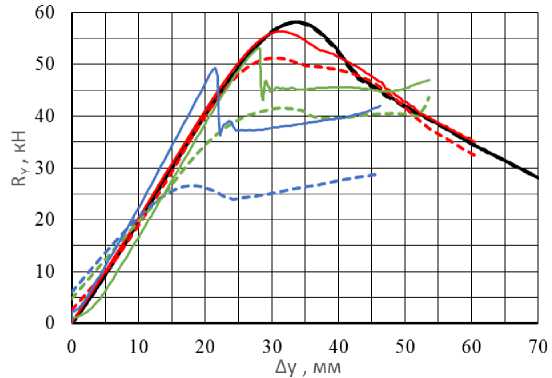
Рис. 7. Зависимость реакции R_Y (∆ y ): сплошные линии ‒ в пакете Ansys ; пунктирные линии ‒ по аналитической модели; черный цвет ‒ реакции при смещении ∆ х = 0 мм; красный цвет ‒ при смещении ∆ х = 10 мм; зеленый цвет ‒ при смещении ∆ х = 20 мм; синий цвет ‒ при смещении ∆ х = 30 мм

Предлагаемая аналитическая модель не описывает работу арочного эластомерного амортизатора при пробое. Для определения места начала пробоя необходимо проведение предварительного моделирования в пакете конечно-элементного анализа или проведение эксперимента на образцах. Таким образом, можно говорить об ограничении применимости предлагаемой аналитической модели по величине сжатия ∆ y при учете боковых смещений ∆ х . Величина указанного ограничения зависит от геометрии амортизатора, в частности его эластомерных стенок (для рассматриваемого амортизатора – 35 мм, т. е. половина от максимально возможного сжатия ∆ y ). С увеличением ∆ х наблюдается увеличение расхождения результатов расчетов R_Y (∆ y ) в пакете Ansys и по аналитической модели. Нужно отметить, что для случая отсутствия поперечных смещений ∆ х зависимость вертикальной реакции R_Y (∆ y ) может применяться до полного сжатия амортизатора.

Заключение

В настоящей статье представлены результаты расчета усилия арочного эластомерного амортизатора при нагружении одновременно вдоль двух осей по аналитической математической модели. Предлагаемая математическая модель, в которой усилие амортизатора определяется как сумма проекций усилий эластомерных стенок, позволяет по известной упругой силовой характеристике сжатия амортизатора оценить его упругую силовую характеристику в боковом направлении.

Рассмотренная в настоящей статье аналитическая модель работы арочного эластомерного амортизатора дает приемлемое для практического применения в имитационном моделировании совпадение результатов расчетов усилий с полученными в пакете конечно-элементного анализа Ansys. Предложенная математическая модель не учитывает смыкание эластомерных стенок, поэтому применяется только в рабочей области амортизатора и не

Том 6

описывает его работу при пробое. Для использова- ские размеры амортизатора и его силовую упругую ния аналитической модели нужно знать геометриче- характеристику на сжатие без бокового смещения.