Аналитическая модель ионного транспорта в интерфейсной области источника ионов ЭРИ АД (электроспрей)

Для совмещения высоковакуумного устройства — масс-анализатора с источниками ионов, работающими при повышенном давлении, обычно используется система с дополнительной ступенью дифференциальной откачки, или интерфейс. Данная область характеризуется специфическими газодинамическими и электрическими условиями формирования и транспортировки ионного пучка, причем этими условиями можно управлять. При движении ионов через интерфейсную область происходит их взаимодействие с молекулами нейтрального газа, в результате чего меняется объем ионного пучка в фазовом пространстве, а также, если имеют место химические реакции, меняется и его состав.

Начиная с первых работ по использованию газодинамической системы типа Канторовица—Грея в масс-спектрометре [1, 2] и до сих пор идет интенсивное исследование процессов, протекающих в интерфейсе [3]. Этот интерес объясняется важностью изучаемых сложных и многофакторных явлений для последующей интерпретации масс-спектрометрических результатов. Так, на характеристики ионного пучка и величину ионного тока на выходе интерфейса влияют давление, конфигурация электродов, формирующих газовый поток, конфигурация и величина электрического поля, а также физико-химические свойства ионов и растворителя.

В данной работе представлена аналитическая модель для расчета транспортирующих свойств интерфейса для источника ионов типа ЭРИ АД (экстракция ионов из растворов при атмосферном давлении). Выбор типа интерфейса продиктован его широкой распространенностью, а также возобновлением работ по ионизации и фрагментации растворов методом ЭРИ АД для целей изотопного анализа.

ОПИСАНИЕ МОДЕЛИ

Традиционно камера интерфейса строилась по принципу генератора молекулярного пучка [2]. Такой тип интерфейса называется также интерфейсом с аксиальным вводом. Типичное давление в этой области составляет 1–100 Па, а для систем типа ЭРИ АД — 100–4000 Па.

Ионы и мелкие заряженные капли из источника ионов попадают в интерфейсную область через небольшое отверстие в стенке масс-спектрометра, представляющее собой сопло, на выходе из которого образуется сверхзвуковая струя. Вниз по течению на одной оси с соплом находится конический отборник (скиммер), служащий для вырезания части газодинамического потока, а также для фокусировки и ускорения ионов в промежутке "сопло—скиммер".

Для описания процессов в интерфейсе мы будем использовать приближение сплошной среды, т. к. обычно число Кнудсена в интерфейсной области удовлетворяет неравенству

Kn = L <<  1. (1)

Здесь l — длина свободного пробега молекул газа, L — характерный масштаб интерфейсной области. Используем для тока ионов стандартное выражение j = vdn + D Vn, (2)

где n — концентрация заряженных частиц в газе, м^–3; D — коэффициент диффузии, м²/с.

Дрейфовая (направленная) скорость ионов в газе vd складывается из скорости движения ионов вместе с нейтральным газом u и скорости движения ионов относительно газа под действием электрического поля K E vd = u + K E,                   (3)

где K — подвижность иона в газе, В - с/м²; E — напряженность электрического поля, В/м.

Мы пренебрегаем влиянием объемного заряда и считаем, что поле E создается только внешними источниками, т. е. электродами (стенкой и скиммером). Это предположение соответствует реальности для токов, характерных для метода ЭРИ АД.

В отсутствие химических реакций ток ионов подчиняется уравнению непрерывности, имеющему в стационарном случае вид

V- j = 0. (4)

Пренебрежем также тепловой диффузией ионов, т. к для большинства ионов, исследуемых методом ЭРИ АД, в интерфейсной области число Пекле удовлетворяет неравенству

Pe = v d L >>  1.              (5)

D

В результате из уравнения (4) с учетом (2) получим уравнение для траектории иона dr = ur (r, z) + KE,(r, z)                  (6)

d z u z ( r , z ) + KE z ( r , z )

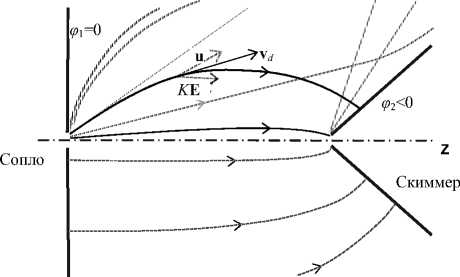
..........линии тока нейтрального газа

— силовые линии электрического поля

— траектория иона

Рис. 1. Геометрия интерфейса, линии тока газа, силовые линии электрического поля и траектории ионов.

u — скорость газового потока; K E — скорость, приобретаемая под воздействием электрического поля; v d — суммарная дрейфовая скорость; ф 1 , ф ₂— потенциалы стенки (сопла) и скиммера

Таким образом, перейдя от анализа плотности ионов к анализу отдельных траекторий, мы можем использовать уравнение (6) для описания свойств ионного пучка. Вид траектории при этом будет зависеть от конфигурации электрического поля, разности потенциалов между соплом и скиммером, параметров газодинамической струи, а также от характера взаимодействия ионов и спутного газа в электрическом поле, определяющего подвижность ионов K (см. рис. 1).

Определим факторы, входящие в уравнение (6).

Газодинамический поток

Для интерфейса в масс-спектрометре характерен большой перепад давлений (порядка 1001000), в результате которого на выходе сопла образуется типичная для сильно недорасширенных струй газодинамическая структура. В окрестности среза сопла скорость газа переходит в звуковую, и далее по течению образуется расширяющаяся струя с плотной сжатой оболочкой (бочка Маха), сверхзвуковым изоэнтропическим ядром и прямым скачком уплотнения (диском Маха), за которым скорость течения скачком переходит в дозвуковую.

Будем считать, что скиммер расположен до диска Маха и отбор ионов из спутного газа осуществляется без возмущения структуры струи.

Поле газового течения в ядре сверхзвуковой струи можно описывать как течение с сохранением энтропии вдоль линий тока [4, 5]. При этом необходимо решать систему уравнений, включающую в себя уравнение неразрывности, уравнение адиабаты и уравнения сохранения компонент импульса (уравнений Эйлера).

Введем полярную систему координат r , 6 с началом в центре выходного среза сопла и углом 6 , отсчитываемым от оси симметрии струи. Будем считать, что струя истекает практически в вакуум (степень нерасчетности очень велика) и занимает некоторый сектор 6 е [0, 6 _max], так что к границам струи ее плотность спадает практически до нуля: p ( 6 _max) = 0. Известно, что при больших r скорость газа в струе достигает своего максимального значения, а линии тока становятся прямыми.

Введем безразмерные параметры

ρ

р*

Р ,

u

^ и , с *

r

--> r .

Здесь и — скорость газового потока, р — плотность, y — показатель адиабаты. Индексом " * " обозначены критические параметры (параметры на линии перехода дозвукового течения в сверхзвуковое); c _* — критическое значение скорости звука; r ₀ — радиус выходного отверстия сопла.

Как показывает анализ, наиболее простые выражения для компонент скорости газа удается получить, положив приближенно показатель адиабаты Y = 3/2, 0 max = п /2 и приняв для плотности в качестве исходного выражения

р (r, 0 ) = —cos² 0 , r

где a = 1 — некоторая константа, значение которой можно отыскать, сшивая полученное решение с решением, справедливым в окрестности линии перехода скорости течения из дозвуковой в сверхзвуковую.

Приведем результат:

и 2 = u max-- cos 0 ,                    (8)

r

2a u„ =-----In 0

ur max

2   4a r —2—cos0 umax sin 0,

где u max — максимальная скорость стационарного вытекания.

Решение (7)–(9) качественно правильно описывает характер течения на любом расстоянии r > 1 от сопла.

Преобразование компонент скорости из полярной системы координат в цилиндрическую дается следующими формулами:

и цилиндрич = u r sin 0 + u ₀ cos 0 , и цидиндрич = u r cos 0 - u ₀ sin 0 .

Электростатическое поле

Для задания электростатического потенциала скиммера воспользуемся результатами работы [6] для конуса с отверстием. Направим ось Z по оси скиммера в сторону большего сечения, а начало координат перенесем в центр скиммера по высоте. Пусть 2 а — длина скиммера, r S — радиус отверстия, 0 s — угол полураствора.

Потенциал конуса описывается следующим выражением:

, _x 2     К ( k ( r , z , V ) )

ф ( ^r , z ) = J , /         / . ^d V ,       ⁽¹¹⁾

- n ^M ( r , z , V ) + L ( r , V )

где

M ( r , z , v ) = ( r_S + a tg 0 _S ) 2 + r 2 + z 2 +

+ 2 a [ tg 0 _S ( r_S + a tg 0 _S ) - z ] sin v + a ² ( 1 + tg² 0 _S ) sin² V ,

L ( r, V ) = - 2 r [ r_S + atg 0 _S + atg 0 _S sin v ] ,

⁽ k ⁽ r ’ z * ⁾⁾ 2 = M ( r , V + l( r , V ) ■

К — полный эллиптический интеграл первого рода.

Для нахождения суммарного потенциала в области между проводящей стенкой и скиммером необходимо воспользоваться методом изображений. Нужно расположить скиммер и его изображение симметрично относительно стенки и вычесть один потенциал из другого в каждой точке пространства.

Компоненты электрического поля связаны с потенциалом известным соотношением

E ( r , z ) = - grad ф _E ( r , z ) ,          (12)

здесь ф _E ( r , z ) — потенциал системы "стенка— скиммер".

Подвижность ионов и ионные траектории

В отсутствие электрического поля средняя скорость ионов в сверхзвуковой струе равна направленной скорости газового потока. Этот факт определен экспериментально, даже для ионов довольно больших масс при не слишком большой разреженности газа в струе [7]. Тогда подвижность иона в газовом потоке можно считать равной подвижности в равновесном газе.

При малой величине электрического поля, когда взаимодействие иона и молекулы воздуха можно рассматривать как поляризационное взаимодействие точечной заряженной частицы с неполярной нейтральной частицей, подвижность иона K не зависит от E и обратно пропорциональна плотности газа [8]:

K poi ( r , z ) =          ,                (13)

p            p ( r , z )

где

/Й л U„

X =------—/^=.

0.596 c , p , N A ^цпа

Здесь E q — электрическая постоянная ( e ₀ = = 8.854 - 10^-12 Ф/м); a — поляризуемость молекул газа, м³ (1.76 - 10^-30 м³ для молекулы N 2 ); / й — молярная масса газа (0.028 кг/моль для воздуха); N A — число Авогадро (6.023 - 10²³ моль^-1); ц — приведенная масса молекулы и иона, кг. По порядку величины параметр % составляет 10^-6 м/В.

При увеличении напряженности электрического поля силы отталкивания между ионом и моле- кулой нарастают. Введем в рассмотрение сечение ст взаимодействия иона и молекулы как сечение столкновения твердых сфер, не зависящее от относительной скорости сталкивающихся частиц.

В случае, когда скорость дрейфа в электриче-

ском поле w значительно превышает тепло-kT вую, w = KE >> —, можно считать [8]

m

w = Z

eE

^ N ct ’

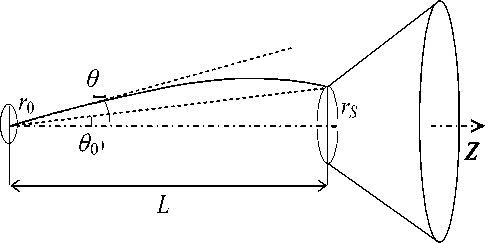
Рис. 2. Геометрия и обозначения к построению ВАХ (уравнение (17)).

rS — радиус отверстия скиммера; L — расстояние от сопла до скиммера; (r0,0) — координаты на чального положения иона

где Z — параметр, близкий к единице. В этом случае выражение для подвижности будет выглядеть следующим образом:

^Khs ( r , z ) = П [ р ( r , z ) E ( r , z ) ] 12 ,        (15)

где

1      erm n =—.-------.

c * V ^ N a P ^ ct

Параметр n по порядку величины составляет 10 ^{- 12}/ СТ м/В. Для сечения ст = 10 ^{- 18} м² этот параметр будет иметь порядок 10^–3 м/В.

ВАХ в параксиальном приближении

В силу симметрии задачи уравнение траектории иона (6) вблизи оси Z можно представить в виде dr

- = F ( z ) r , d z

где F ( z ) — первый член разложения в ряд по r правой части уравнения (6) в окрестности значения r = 0.

Интегрируя уравнение (16), получим, что ион, вышедший из точки ( r_o, 0 ) , при пересечении плоскости входного отверстия скиммера z = L будет иметь координату r , равную (см. рис. 2)

r = r _osin 0 exp

( L

J F(z)dz r0 cos 0

Пусть I ₀ — ток ионов через входное отверстие скиммера в отсутствие электрического поля, а I — ионный ток в случае, когда между соплом и скиммером приложена разность потенциалов A U. В пределе малых углов 0 и 0 _О отношение токов можно выразить как

4 ° 1 2 ¹ о 1 ⁰ О ,

Написав 0 _О = r / L и выразив 0 из формулы (17), приходим к окончательному выражению для вольтамперной характеристики ионного тока через отверстие скиммера в параксиальном приближении

I ,        L 1 2      ( L ^

—(U ) = — exp - 2j F ( z , A U )d z .

¹ 0          I r 0 J I r o                 J

Легко убедиться, что при A U = 0 формула (19) дает I / I 0 = 1, как и должно быть.

ЗАКЛЮЧЕНИЕ

В работе дано краткое описание аналитической модели для расчета параметров интерфейсной области источника ионов типа ЭРИ АД. Показано, как на основе предложенной модели рассчитать сглаженные траектории ионов и с их использованием построить ВАХ (зависимости ионного тока через входное отверстие скиммера от разности потенциалов между соплом и скиммером). Выделены управляющие параметры модели, по которым можно определить, как тип иона влияет на ВАХ. Предложены аналитические формулы для расчета ВАХ в параксиальном приближении, т. е. в пределе слабого электрического поля.

В подробной публикации будут проведены анализ изменения фазовых характеристик ионного пучка в интерфейсе ЭРИ АД, а также сравнение полученных данных с экспериментальными.