Аналитическая модель обеспечения информационной безопасности образовательных организаций системы общего и среднего образования

Информация, которая распространяется по средствам коммуникации [8], иногда имеет противоречивое содержание и негативную направленность, которая может повлиять на социально-нравственные ориентиры личности [1].

Средства массовой информации оказывают существенное влияние на окружающих. Насилие и жестокость, которые могут содержаться в информации [16], порой подаются без цензуры [5]. Особенно восприимчивы к негативной информации дети, у которых только формируются нравственные идеалы и стереотипы поведения в обществе [6]. Полностью оградить подрастающее поколение от негативной информации, которая их окружает, не получится, но научить правильно воспринимать информацию [2], ее анализировать и думать о последствиях под силу опытным учителям и педагогам [3]. В связи с этим возникает необходимость о включении в программы общего и среднего образования обучения компетенциям в области информационной безопасности (ИБ) [4].

В связи с этим на первый план выносится задача создания безопасной информационной среды [10], которая будет благоприятно влиять на развитие личности обучающегося и формировать ее [9].

78 в ыпуск 4/2020

Описание модели ИБ образовательной организации (ОО)

Временные интервалы между моментами обнаружения негативных факторов [18] являются случайными [11]. Выявленные негативные информационные воздействия (НИВ) образуют поток, который близок к распределению Пуассона [12]. Временные интервалы, затраченные на обнаружение НИВ окружающей среды с требуемым признаком, также являются случайными величинами [17]. Полученные данные о признаках НИВ внешней среды [13] обрабатываются информационно-аналитической системой и после однозначной идентификации нейтрализуются по мере возможности [15]. Тем самым решается задача по нейтрализации информационных угроз (ИУ) ОО [7].

Рассмотрим случай, когда НИВ внешней среды [14] возникают с частотой, соизмеримой со временем реакции системы на идентификацию обнаруженных ИУ и их своевременную нейтрализацию системой ИБОО.

Рассмотрим всевозможные состояния, в которых может находиться моделируемая система ИБОО в определенный этап времени:

Р ₀₀ – система обнаружения ИУ и система нейтрализации выявленных ИУ находятся в состоянии ожидания;

Р ₁₀ – система обнаружения выявила наличие ИУ и выполняет ее идентификацию, система нейтрализации выявленных ИУ находится в состоянии покоя;

Р ₀₁ – система обнаружения ИУ находится в состоянии покоя, а система нейтрализации выявленных ИУ занята обработкой информации о факте информационного воздействия (ИВ) и принимает меры по нейтрализации выявленной угрозы;

Р ₁₁ – система обнаружения ИУ обнаружила факт ИВ и идентифицирует его, а система нейтрализации выявленных ИУ занята обработкой информации о факте ИВ и принимает меры по нейтрализации выявленной угрозы.

Опишем все состояния, в которых может находиться система ИБОБ, функционирующая в условиях деструктивного воздействия внешней среды.

Первое состояние. Состояние ожидания НИВ системой ИБОБ. Данное состояние возможно в следующих случаях:

• •    в момент времени t система обнаружения ИУ и система нейтрализации находятся в состоянии ожидания. За временной интервал Δ t в области действия систем идентификации и нейтрализации не появилось ни одной угрозы. Вероятность данного факта

Р ₀₀ ( t )(1 – λ Δ t );                                    (1)

• •    в момент времени t система идентификации и нейтрализации находилась в состоянии обработки выявленной угрозы. За время Δ t данные об выявленной угрозе ИБ идентифицированы, производятся мероприятия по нейтрализации НИВ. Вероятность данного факта

Р01(t)v2Δt.(2)

Соответственно, состояние системы ИБ запишется в следующем виде:

Р00(t + Δt) = Р00(t)(1 – λΔt) + Р01(t)ν2Δt.(3)

После соответствующих преобразований и перехода к пределу при Δ t → 0 запишем состояние системы в виде дифференциального уравнения:

d Р00(t) = –Р00(t)λ + Р01(t)ν2.(4)

dt

Нечай А.А., Краснов С.А., Свинарчук А.А. Аналитическая модель обеспечения... 79

Второе состояние. Данное состояние возможно в следующих случаях:

• •    в момент времени t система находится в состоянии ожидания ИВ, за интервал времени Δ t в области действия системы идентификации и нейтрализации не проявилось ни одного нового факта ИВ, не было нейтрализовано ни одной угрозы ИБ. Вероятность данного факта

Р ₀₁ ( t )(1 – λΔ t )(1 – ν ₂ Δ t );                               (5)

• •    в момент времени t система ИБ находилась в режиме выявления факта ИВ, за промежуток времени Δ t система ИБ передала данные о выявленном факте ИВ в систему идентификации и нейтрализации. Вероятность данного факта

Р ₁₀ ( t )( ν ₁ Δ t );                                          (6)

• •    в момент времени t система ИБ находилась в состоянии обнаружения факта ИВ и параллельно обрабатывала информацию об ИВ, а также принимала меры по нейтрализации выявленной угрозы, была полностью загружена. За интервал времени Δ t система ИБ обнаружила и выдала данные о выявленном факте в систему идентификации и нейтрализации, но система ИБ эти данные не использовала, так как была занята обработкой данных о предыдущем факте ИВ. Как следствие – данные о факте ИВ, полученные от системы обнаружения, были безвозвратно потеряны вследствие кратковременности пребывания фактора в области действия системы идентификации и нейтрализации НИВ. Вероятность данного факта

Р ₁₁ ( t ) ν ₁ Δ t .                                              (7)

Соответственно, дифференциальное уравнение описывающее состояние системы ИБОО, запишется в следующем виде:

d Р ₀₁ ( t ) = – Р ₀₁ ( t )(λ + ν ₂ ) + Р ₁₁ ( t ) ν ₁ + Р ₁₀ ( t ) ν ₁ .                      (8)

dt

Третье состояние. Данное состояние возможно в следующих случаях:

• •    в момент времени t система ИБОО находилась в состоянии покоя, за временной интервал Δ t в области действия системы выявления ИУ был обнаружен факт НИВ. Вероятность данного факта

Р ₀₀ ( t )λΔ t ;                                         (9)

• •    в момент времени t система ИБ находилась в режиме обнаружения факта НИВ, но информация об данном факте еще не была идентифицирована и нейтрализована; за интервал времени Δ t в области действия системы обнаружения ИВ проявилось очередное ИВ, данное воздействие не было идентифицировано и нейтрализовано системой ИБ. Вероятность данного факта

Р ₁₀ ( t )(1 – ν ₁ Δ t );                                    (10)

• •    в момент времени t система ИБ была полностью загружена, был обнаружен факт ИВ, проводилась идентификация и нейтрализация выявленного факта, за интервал времени Δ t источник НИВ был идентифицирован, были приняты меры по его нейтрализации. Вероятность данного факта

  
  

Р ₁₁ ( t ) ν ₂ Δ t.

80 в ыпуск 4/2020

Соответственно, дифференциальное уравнение для вышеописанного состояния системы ИБОО запишется в следующем виде:

d Р ₁₀ ( t ) = Р ₀₀ ( t )λ – Р ₁₀ ( t ) ν ₁ + Р ₁₁ ( t ) ν ₂ .                         (12)

dt

Четвертое состояние. Данное состояние возможно в следующих случаях:

• •    в момент времени t система ИБ находилась в состоянии идентификации и нейтрализации выявленного факта ИВ, за интервал времени Δ t получены новые данные об обнаруженных ИВ. Вероятность данного факта

Р ₀₁ ( t )λΔ t ;                                        (13)

• •    в момент времени t система ИБ находилась в состоянии обнаружения, идентификации и нейтрализации выявленного факта НИВ, за временной интервал Δ t не были обработаны данные по факту выявления ИВ, а в области действия защитной подсистемы появились новые факты НИВ. Вероятность данного факта

Р ₁₁ ( t )(1 – ( ν ₁ + ν ₂ )Δ t ).                               (14)

Следовательно, дифференциальное уравнение для вышеописанного состояния системы ИБОО запишется в следующем виде:

d Р ₁₁ ( t ) = Р ₀₁ ( t )λ – Р ₁₁ ( t )( ν ₁ + ν ₂ ).                            (15)

dt

Полученная система дифференциальных уравнений, описывающая все имеющиеся состояния системы ИБОО, функционирующей в условиях негативного воздействия окружающей среды, запишется в следующем виде:

d Р ₀₀ ( t ) = – Р ₀₀ ( t )λ + Р ₀₁ ( t ) ν ₂ ;

dt

Р ₀₁ ( t ) = – Р ₀₁ ( t )(λ + ν ₂ ) + Р ₁₁ ( t ) ν ₁ + Р ₁₀ ( t ) ν ₁ ;

dt d Р10(t) = Р00(t)λ – Р10(t)ν1 + Р11(t)ν2;

dt d Р11(t) = Р01(t)λ – Р11(t)(ν1 + ν2).                          (16)

dt

Для стационарных процессов предполагаем, что переходные процессы в системе отсутствуют. Это позволяет сделать следующую запись свойств для вероятностей перехода: t → ∞, ddt Р_ij ( t ) → 0, Р_ij ( t ) = Р_ij ( t ) = const.

Тогда полученная система дифференциальных уравнений, описывающая все имеющиеся состояния системы ИБОО, преобразуется в систему алгебраических уравнений:

Р ₀₀ ( t ) λ = Р ₀₁ ( t ) ν ₂ ;

Р ₀₁ ( t ) (λ + ν ₂ ) = Р ₁₁ ( t ) ν ₁ + Р ₁₀ ( t ) ν ₁ ;

Р ₁₀ ( t ) ν ₁ = Р ₀₀ ( t ) λ + Р ₁₁ ( t ) ν ₂ ;

Р ₁₁ ( t ) ( ν ₁ + ν ₂ ) = Р ₀₁ ( t ) λ,                                 (17)

где λ – интенсивность потока НИВ; ν ₁ – интенсивность выявления НИВ системой ИБ; ν ₂ – интенсивность идентификации и нейтрализации выявленных негативных ИВ.

Нечай А.А., Краснов С.А., Свинарчук А.А. Аналитическая модель обеспечения...    81

Система алгебраических уравнений, описывающая все возможные состояния системы ИБ:

Р

Р ₀₀

ν1ν2

λ(λ + ν₁ + ν₂) + ν₁ν₂ ^;

^-V 2 ^(- + ^V 1 ^{+ V} l )

10 (v + ^лш- + v + ^v 2 ) + ^v i ^v 2 ^] ;

=           ^ν1λ           ;

λ(λ + ν₁ + ν₂) + ν₁ν₂

^Р 11

^V 1

(vt + v2)[A(A + v1 + v2) + vtv2]

Соответственно, вероятность того, что выявленный факт НИВ будет идентифицирован и распознан системой ИБОО, составит

Р _обсл ( t ) = Р ₀₀ ( t ).

Физически процесс обнаружения, идентификации и нейтрализации фактов НИВ состоит в «прореживании» λ* – потока негативных фактов ИВ, где λ* – это поток негативных фактов ИВ, не обнаруженных, не идентифицированных и не нейтрализованных:

λ^* = λ P _отк ,                                      (20)

где Р – вероятность того, что факт НИВ не будет обнаружен системой ИБ.

Р _отк = 1 – Р _обсл .                                      (21)

На рисунке изображен график зависимости вероятности обнаружения, идентификации и нейтрализации фактов ИВ от интенсивности задействования подсистем обнаружения, идентификации и нейтрализации.

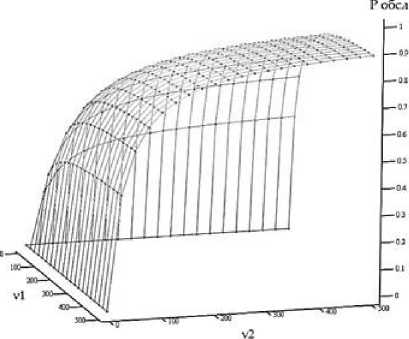
Зависимость обнаружения, идентификации и нейтрализации фактов ИВ

Если проанализировать полученный график, можно увидеть, что с увеличением фактов проявления НИВ подсистемы обнаружения, идентификации и нейтрализации с такой же пропорциональностью загружаются обработкой данных фактов.

82 в ыпуск 4/2020

Заключение

Предложенная модель позволяет оценить эффективность работоспособности системы информационной защиты ОО, прогнозировать результаты обработки выявленных фактов ИВ и выработать определенные требования для поддержания системы ИБ образовательной организации в рамках требуемого показателя эффективности.