Аналитическая модель оценки предела выносливости сварных соединений феррито-перлитных сталей

Введение. Микродефекты и зоны с концентрацией напряжений в сварных соединениях обусловливают появление усталостных макротрещин. Подобные повреждения потенциально опасны, особенно если ресурс усталостной прочности конструкции практически исчерпан. В этом случае размер трещины близок к критическому значению, и крайне важно определить ее длину. Статья посвящена разработке инженерной аналитической модели для оценки критической длины трещины и предела выносливости сварных соединений с образовавшимся зерном в структуре феррито-перлитных сталей после сварки.

Следует отметить, что сварное соединение, равнопрочное для статического нагружения, не гарантирует его надежности при циклических нагрузках. Это обусловлено локальными пластическими деформациями в местах концентрации напряжений в прерывистых связях конструкций, подверженных циклическим нагрузкам [1]. Можно предположить, что для пластичных материалов максимальные напряжения в этих зонах будут постоянными и равными пределу текучести, если пренебречь некоторым упрочнением материала в местах концентрации напряжений и принять, что области возмущенных напряжений относительно малы по сравнению с толщиной материала [ 2 ] .

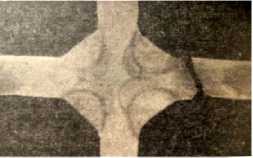
Материалы и методы. Предел выносливости конструкционных сталей приближенно соответствует значениям о -1 = 0,5 ... 0,7о_т, а разрушение при циклических напряжениях, как правило, происходит локально в виде трещин, берущих начало от концентраторов напряжений или дефектов сварного соединения (рис. 1).

б )

в )

г )

Рис. 1. Трещины в месте подреза и в шве: ( а , б ) разрушения крестовых соединений от трещины при неполном проплавлении; ( в ) и в зоне термического влияния (ЗТВ); при полном проплавлении ( г ) [2]

Концентрация напряжений, возникшая в результате недостаточного проплавления при формировании сварного соединения, также может играть решающую роль в образовании слабых зон. Этому способствуют значительная неоднородность механических характеристик, серьезные дефекты шва и околошовной зоны.

В угловых и тавровых соединениях (с разделкой кромок или без нее) в большинстве случаев трещина начинается от концентратора напряжений (рис. 1 в , г ). Если шов выпуклый, разрушение может происходить по зоне сплавления или вблизи нее — по основному металлу в ЗТВ, структура которого претерпела изменения [3].

С течением времени микродефекты приводят к возникновению усталостных трещин [4, 5]. Такие трещины в сварных соединениях некоторых элементов распространяются медленно, поэтому могут быть не особо опасны. Об этом свидетельствует практика использования современных марок сталей для корпусов судов [6]. В то же время усталостные трещины потенциально опасны в двух случаях.

• 1.    Если практически исчерпан ресурс, обеспечиваемый статической неопределимостью конструкции и другими факторами.

• 2.    Если размер трещины соответствует Гриффитсовой критической длине в бесконечной пластине L|_{CT -1} = L_c, определяемой зависимостью:

L = (K i _c/o _i )²/n, (1) где K_1c — критический коэффициент интенсивности напряжений при плоской деформации в вершине трещины; 0 -1 — напряжение предела выносливости материала; L — половина длины сквозной тещины.

Коэффициент K_1c может быть рассчитан на базе стандартного набора механических характеристик и среднего диаметра зерна феррито-перлитной стали согласно [ 7 ] для плоской деформации и по [8] для плосконапряженного состояния. Однако, чтобы найти критическую длину трещины предела выносливости, необходимо знать величину 0 -1 .

Механизм влияния среднего диаметра зерна стали в момент начала перехода трещины в лавинообразное продвижение, вероятно, отличается от механизма, контролирующего ее продвижение на стадии образования. Такие предположения, основанные на результатах исследований [7, 9–11], обусловливают более подробное рассмотрение процессов, контролирующих окончание стадии стабильного развития макротрещины при напряжениях, равных пределу выносливости. Его при критических размерах трещины не сложно определить по (1), если найти закономерности влияния структуры, пластических свойств и механических характеристик материала на размер критической трещины.

Цель данного исследования — разработка аналитических зависимостей, позволяющих установить взаимосвязь между критической длиной трещины при напряжениях 0 -1 , механическими характеристиками феррито-перлитной стали и средним диаметром зерна в структуре металла. Задача — довести полученные зависимости до инженерных формул, позволяющих оценивать предел выносливости феррито-перлитных сталей.

Механика

Результаты изучения процесса трещинообразования при высоких номинальных напряжениях свидетельствуют о дискретном, скачкообразном их развитии [12]. Такой характер роста демонстрирует моделирование на окончательной стадии разрушения [7] при нагрузке, соответствующей пределу выносливости. Это говорит о том, что после накопления односторонней пластической деформации пластическое деформирование сдерживается, если к вершине трещины примыкают большие объемы материала с фрагментированной структурой.

Результаты исследования. При высокой плотности дислокаций, создающих фрагментированную структуру, примем условия плоской деформации в вершине трещины. Дополнительные условия будут обеспечиваться за счет стеснения и набранной односторонней пластической деформации под циклическими нагрузками. Запишем постулаты для момента, когда L = L_Kp, о = О -1 .

• 1.    Односторонняя пластическая деформация достигает критической величины в вершине трещины.

• 2.    Фрагментация (ячеистость) структуры феррито-перлитного материала предельна (находится на втором уровне).

• 3.    Функция разности раскрытия берегов и вершины трещины имеет перегиб в точке, близкой к состоянию, когда L = L_Kp, о = О -1 .

Из экспериментальных данных следует, что циклическое нагружение металлов вызывает значительное изменение структуры, субструктуры и влияет на все особо чувствительные характеристики. Например, увеличение числа циклов нагружения циклически упрочняющихся (или разупрочняющихся) металлов способствует повышению (или понижению) твердости (прежде всего на поверхности исследуемых образцов) [13,14].

Результаты упругопластического анализа пластических зон в вершине трещины, определенные по модели Панасюка-Дагдейла [15], существенно отличаются от реальных для материалов с показателем упрочнения m > 0,05. Тем не менее будем считать, что при небольших номинальных напряжениях он = о—1 раскрытие в вершине трещины 6 и отношение 6/гр могут быть определены достаточно точно для случая плоской деформации по формулам [16]:

6 = 8от • L/pi/E • lnsec[поH/2/оT],

- ,   8б т ln sec(na _H /2)

n(sec(nff H /2)-1)

где гр — линейный размер пластической зоны на продолжении трещины от ее вершины (рис. 2); ет — деформация предела текучести.

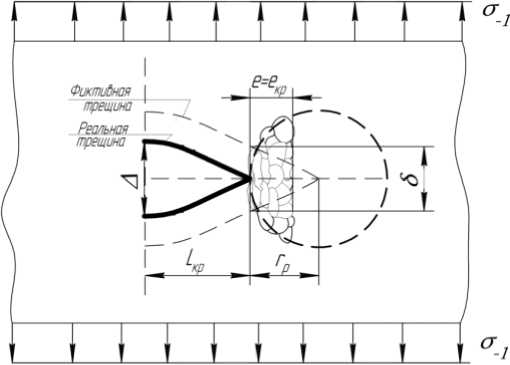
Рис. 1. Состояние металла в вершине критической трещины нормального отрыва под напряжениями предела выносливости

Оценим раскрытие берегов этой трещины при номинальных напряжениях ниже предела пропорциональности, допуская некоторую погрешность [ 16 ] :

Д = ^ .                                    (3)

После дифференцирования разницы между 6 и Д находим, что напряжения, соответствующие моменту ускоренного сближения 6 и Д, будут соответствовать номинальным, определяемым по выражению:

О н = О т^/ 2.                                                     (4)

При значительных пластических деформациях структура материала претерпевает фрагментацию в вершине трещины, поэтому величина екр связана со стадийностью и способностью к деформированию фрагментированной структуры. По А. М. Глезеру [17], граница между макропластической и мегапластической деформациями условна, находится на уровне относительной деформации, равной стопроцентной, или истинной. При этом значение критической деформации:

^Скр ~ 1.

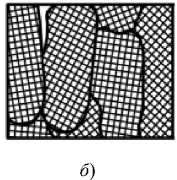
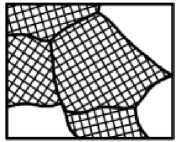
А. Н. Балахнин¹ отмечает, что самоорганизация структуры с образованием ячеек (рис. 3) начинается уже при деформации феррита стали 09Г2С и при среднем значении степени холодной деформации е 15-35%.

в )

Рис. 3. Микроструктура при пластической деформации: е = 80 % ( а ), е = 40 % ( б ), е = 1 % ( в ), е = 0 % ( г ) [11]

При дальнейшем увеличении деформации происходит утонение стенок ячеек и уменьшение их размера. Фрагменты приобретают вытянутую форму, зерна вытягиваются в направлении пластического течения (рис. 3).

При критическом раскрытии трещины в области, примыкающей к вершине, на модели фиктивной трещины структура зерен должна стать вытянутой, перейти в предскольное состояние (рис. 3 а). Она, вероятно, будет сформирована за счет сдерживания подтока новых дислокаций и перехода их через границы зерен. Материал в данной области должен быть в состоянии предельной критической пластичности, а линейная характеристика его фрагментов — на втором фрагментарном уровне. Очевидно, что в примыкающей зоне пластичности у трещины также должно быть некоторое количество зерен в их предельном пластическом состоянии.

Итак, зона может быть образована за счет накопления части односторонней пластической деформации, охватывающей практически все стадии развития трещины. Однако наиболее существенный вклад в увеличение такой деформации вносится на окончательной стадии разрушения, когда область пластичности велика не только по отношению к длине трещины, но и к линейной характеристике структуры металла. В этой зоне зерна имеют вытянутую форму в виде продолговатой рисинки с размером поперечного сечения d_к.

Отнесем средний диаметр зерна недеформированного материала dz к dк. Тогда для второго фрагментарного уровня:

dz/dк = 1/0,618/0,618 = 2,618,                                  (6)

где dк — диаметр фрагмента.

Не трудно заключить, что для этого состояния пластическая деформация может быть определена по зависимости максимального равномерного удлинения [3, 14]:

е_кр = 2 ln(d_z/d_к') = 2.

Для этого же состояния критическая пластическая деформация на испытываемом образце в шейке при разрыве выражается известной зависимостью:

б кр = к_нЛп ( ^-ф ),                                       ⁽⁸⁾

где кн — коэффициент нормирования, введенный авторами для перехода от структуры в критическом пластическом состоянии к значению критической пластической деформации образца при разрыве.

Найдем этот коэффициент через относительное (критическое) сужение образца при разрыве, приравняв

(9) к (8). Тогда с учетом (6) критическая пластическая деформация определяется по выражению:

Скр

= 2 = ln — —+ ln —— = 2 ln —— . ^1-Ф к       ^1-Ф к         ^1-Ф к

Для критического раскрытия в вершине трещины структурно-деформационный критерий можно

Механика

выразить:

б кр = ^б кр = 2d_zZnf 1 _-y.                                    (10)

В результате влияния критического поперечного сужения ф_к на коэффициент интенсивности напряжений при плоской деформации К_1С для высокопрочных сталей отмечены [ 18 ] :

• —    значительный разброс значений К_1С и ф_к;

• —    удовлетворительная корреляция между ними.

При этом заключается, что взаимосвязь К1С и фк можно применять только как качественную. С такими выводами можно согласиться, но только если отбросить взаимосвязь с некоторыми другими структурными характеристиками, например средним диаметром зерна стали и пр.

Для нахождения искомой зависимости подставим (5) в (2). Полученное выражение приравняем к (11) и запишем его относительно L. В результате выкладок получим критическую длину макротрещины для номинальных напряжений, равных пределу выносливости при наиболее опасной асимметрии цикла:

Lkp|      = 0,3607 — 2dz ln f—).(11)

кр|ан=а-1     '       °т    z У1-фк/

Из этого следует, что длина критической трещины прямо пропорциональна величине критической логарифмической пластической деформации е_кр стали и обратно пропорциональна деформации текучести о_т/Е. Преобразовав численную постоянную, (12) можно записать в виде:

Lкр| _ а = 0,7214   "к.(12)

°н_°-1

Используя эмпирическую зависимость сопротивления микросколу зерна R_Mc = о в /(1 — Ф 2 ), справедливую для группы феррито-перлитных низкоуглеродистых сталей, находим средний диметр зерна:

dz =[5,7(1 — фЮ/^в]2.(13)

Здесь ов — предел прочности стали. Подставляя dz в (13), можно получить искомую простую формулу для оценки Lкр, в которую входят только основные характеристики материала.

Для вычисления предела выносливости симметричного цикла достаточно приравнять (12) к (1). Чтобы найти К1С, воспользуемся выводом, полученным в [7]. Окончательная формула для расчета К1С при условиях плоской деформации в вершине трещины строго математически имеет вид:

К 1 _С

п 0,618 d_z     р^сЛП ¹"-¹

[а _т ^1/т-1 -(1-2р) 2 ]/2 У q /

Здесь R_Mce — сопротивление микросколу деформированного металла, которое для класса феррито-перлитных сталей составляет R_Mce = 1,618R_Mc; R_Mc — сопротивление микросколу ферритного зерна; m — коэффициент (показатель) степенного упрочнения материала; q — коэффициент перенапряжения, равный для данного случая 1 — 2D /V3; ц — коэффициент Пуассона. D — коэффициент, который учитывает повышение первого главного напряжения в случае сложного напряженного состояния. Для плоской деформации он принимает значение (1 + m)(1 — 2ц)/2.

Сопротивление микроскола зерна вычисляется по классической зависимости RMc = 5,7/^d для скола ферритного или феррито-перлитного зерна. Выполнив подстановку (15) со всеми составляющими из (12) в (1), получаем окончательное значение предела выносливости в зависимости от стандартного набора механических характеристик материала и среднего диаметра зерна:

J i/m+1

0 -1 =

1,091f ⁴ ' ⁶¹¹ ' ⁽¹ -l ^)(m+1) )      .° _т2-1/т

.                                           .

Если значение среднего диаметра зерна dz неизвестно, его можно вычислить по (14).

Результаты численного тестирования предела выносливости показывают, что зависимость (16) «чувствительна» к некоторым характеристикам материала. Например, варьирование значения коэффициента Пуассона в сотых долях может изменить результат в V2 раз. Вероятно, такая погрешность расчетов связана с особенностью используемых моделей и принятыми допущениями при выводе (16).

Проверим адекватность предложенной аналитической модели на примере группы феррито-перлитных сталей (таблица 1).

Таблица 1

Марка стали	от, МПа	ов, МПа	Ц	т	Ф к	d3, мкм	К1с, МПа	o_v МПа
Сталь 10	190	320	0,3	0,17	0,73	66	103,6	135,41
Ст3сп	270	450	0,3	0,16	0,71	37	101	1921
22К	310	540	0,3	0,16	0,69	30	97	2201
Сталь 50	350	680	0,3	0,16	0,62	25	78	2471
37ХН3А	743	1014	0,26	0,12	0,6	143	73	4801
15Г	280	490	0,29	0,1561	0,65	454	—	230
09Г2	300	440	0,29	0,16	0,69	33	—	235
30ХГСА	1360	1750	0,26	0,132	0,44	74	–	490
16Г2АФ	417	600	0,29	0,16	0,5	22	–	255
10ХСНД	390	540	0,29	0,1322	0,71	274	–	284

1 Значения получены расчетом [7].

² Расчет по зависимости т = [0,75 • г,д[ст_в(1 + 1,4ф к )/а₀ , ₂]}/1д [10⁵ • In (фф) /(200 + 0,5ст₀ , ₂)] [ 2 ] .

3 Вычислено по данным сопротивления микроскола недеформированного материала.

4 Расчет по зависимости (14).

Основные экспериментальные и расчетные характеристики сталей

Для сопоставления результатов, полученных по (12), находим критические длины трещин по экспериментальным данным и с учетом формулы (1). Пределы выносливости рассчитываем при условии плоской деформации по методу [7], который учитывает средний диаметр зерна, коэффициент упрочнения т и другие механические характеристики, существенно влияющие на предел выносливости.

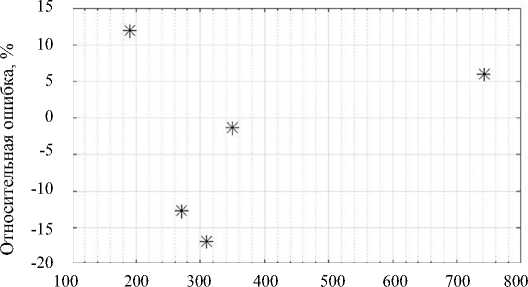
На рис. 4 а представлены значения критических длин сквозных трещин на пределе выносливости для сталей с разными пределами текучести. Расчетные величины по (12) сопоставлены с экспериментальными данными. Сравнение показало достаточно хорошее согласование для феррито-перлитных сталей разной прочности, несмотря на принятые многочисленные допущения (рис. 4 б ).

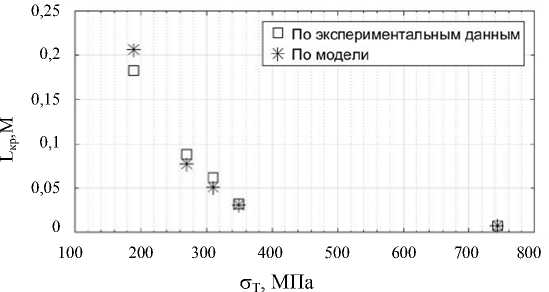
а )

а _т, МПа

б )

Рис. 4. Значения критических длин трещин сталей в зависимости от предела текучести ( а ) и относительная погрешность модели ( б )

Механика

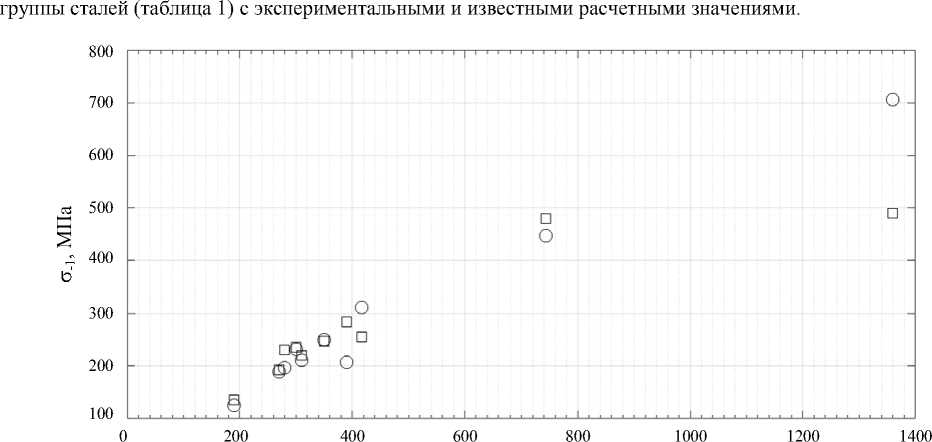
На рис. 5 показаны результаты сравнения предела выносливости симметричного цикла по (16) для

σ T , МПа

Рис. 5. Сравнение пределов выносливости симметричного цикла и пределов текучести: ○ — расчет по модели (16);

□ — известные данные (таблица 1)

По результатам сравнительного анализа можно сделать выводы.

• 1.    Чем прочнее сталь, тем больше сказывается «чувствительность» (16) к исходным данным и растет погрешность расчетов.

• 2.    Для феррито-перлитных сталей с σ_т< 400 МПа результаты расчета пределов выносливости удовлетворительно согласовываются с исходными данными таблицы 1.

Зависимость (16) обладает высокой «чувствительностью» к некоторым исходным параметрам, поэтому на данном этапе исследования невозможно более точно оценить результаты.

При приближении длины трещины к критическому значению L кр она начинает расти скачкообразно. Поэтому детерминистическая модель не может точно определить, через сколько циклов закончится такое развитие трещины, и она распространится со скоростью звука. Средний диаметр зерна материала может значительно различаться в зонах сварных конструкций — например, в ЗТВ и материале, на который не повлияла сварка. Следует учесть, что стадия развития макротрещины на воздухе для элементов крупногабаритных деталей без концентраторов напряжений занимает по времени почти 20%. В связи с этим при определении L _кр относительную погрешность до ∼ 15% можно считать положительным результатом. В рамки этой погрешности попадает период так называемого «циклического долома» [11], где для низких циклических усталостных напряжений ∼ 1/10 часть остаточного ресурса соответствует возрастанию длины трещины примерно в два раза.

Таким образом, предложенные на основе критериев структурно-деформационного анализа аналитические зависимости могут быть использованы в расчетах предела выносливости судовых и других крупногабаритных конструкций.

Обсуждение и заключение. Для безопасной эксплуатации морских судов необходима актуальная и адекватная информация о состоянии конструкций корпуса, в том числе о металлургических дефектах и конструктивных концентраторах напряжений. Важны оценка остаточного ресурса и, соответственно, определение критических размеров усталостных трещин. В вершине критической развивающейся макротрещины при напряжениях, соответствующих пределу выносливости, накапливается односторонняя пластическая деформация, которая снижает пластичность сильно фрагментированной зоны. При этом количество циклов остаточного ресурса остается незначительным и сильно зависит от предела текучести, дефектов, диаметра зерна стали конструкции, в которой развивается трещина.

В результате исследования установлено, что при напряжениях, соответствующих пределу выносливости стали, сближаются скорости раскрытия критической трещины вершины и берегов. Этот момент энергетически примерно соответствует переходу трещины в нестабильное состояние. Накопление односторонних пластических деформаций приводит к предельному состоянию пластичности области, примыкающей к вершине трещины и лавинообразному или резко ускоренному ее движению. Эта критическая область взаимосвязана с диаметром зерна материала, характеристикой критической пластичности и критическим раскрытием в вершине трещины на пределе выносливости.

Полученные аналитические зависимости позволяют с учетом среднего диаметра зерна ферритоперлитной стали и критического сужения рассчитывать предел выносливости наиболее опасного цикла нагружения по классической Гриффитсовой взаимосвязи между длиной трещины, напряжениями и коэффициентом интенсивности напряжений.

Предложенные математическая модель и подход на основе критериев структурно-деформационного анализа могут быть использованы в инженерных расчетах машиностроительных, судовых конструкций и их соединений для оценки эксплуатационного ресурса.