Аналитическая модель околопланетной ударной волны для различных направлений магнитного поля, основанная на МГД-расчетах

Поскольку подробные магнитогидродинамические (МГД) или кинетические расчеты положения и формы околопланетных ударных волн (УВ) трудоемки, требуют значительного времени и поэтому не позволяют отслеживать перемещение УВ в реальном времени, обычно в исследованиях используются эмпирические модели [Fairfield, 1971; Formisano, 1979; Slavin, Holzer, 1981; Nĕmeček, Šafránková, 1991; Peredo et al., 1995; Fairfield et al., 2001; Chapman, Cairns, 2003; Jelínek et al., 2012; Meziane et al., 2014] . Однако такие модели применимы в области параметров солнечного ветра, использовавшихся при их построении, и ограничены в пространстве областью, в которой проводились измерения. М.И. Веригин разработал метод физического аналитического моделирования, в котором используются теоретические выражения с небольшим числом свободных параметров [Веригин и др., 1999; Verigin et al., 1997, 2001a, b, 2003a, b; Веригин, 2004; Kotova et al., 2005] . Параметры определяются из сравнения с экспериментальными данными или численными решениями. Построенные аналитические модели легко применимы для описания различных явлений в околопланетном пространстве при любых условиях в солнечном ветре.

Аналитическая модель УВ в случае препятствий различной формы в газодинамическом (ГД) приближении представлена в работе [Verigin et al., 2003a] . На основе этой модели с использованием точного аналитического решения для угла наклона УВ на бесконечности к направлению невозмущенного солнечного ветра [Verigin et al., 2003b] строится модель УВ в МГД-приближении.

СИСТЕМА КООРДИНАТ И УГОЛ СКОШЕННОСТИ УДАРНОЙ ВОЛНЫ

Для описания УВ используется геоцентрическая система координат GIPM (Geocentric InterPlanetary Medium). В этой системе координат ось X противоположна направлению невозмущенного солнечного ветра. Ось Y направлена так, что вектор межпланетного магнитного поля (ММП) лежит во втором — четвертом квадрантах плоскости XY. Ось Z дополняет систему координат до правой [Bieber, Stone, 1979] . Для моделирования ударной волны, образующейся в сверхзвуковом сверхальфвеновском потоке набегающей плазмы около препятствий различной формы, использовались подробные магнитогазодинамические расчеты, выполненные в Мичиганском университете. Расчеты проводились для препятствий двух видов: полусферы с вытянутым цилиндрическим хвостом и параболоида вращения. Все расчеты проводились в единицах расстояния до магнитопаузы r o .

В газодинамическом (ГД) приближении при обтекании осесимметричного препятствия потоком газа (плазмы), направленным вдоль его оси, форма УВ осесимметрична. Присутствие же ММП в потоке солнечного ветра приводит к дополнительному

(по сравнению с аберрацией из-за орбитального движения планеты) отклонению носовой части УВ от оси Х в плоскости XY системы координат GIPM. Если определить нос МГД ударной волны как ту ее точку, за которой плазма за УВ течет по нормали к фронту, условия Рэнкина—Гюгонио позволяют получить соотношение для угла отклонения потока плазмы в носовой точке a _vn [Веригин, 2004] . Этот угол между направлением набегающего потока и нормалью к поверхности ударной волны в носовой точке будем называть углом скошенности ударной волны:

tg αvn

(1 - e^)sin2( 9 b _V - ^a vn )

• ²    ( ⁸ M A cos^{2 a} vn - cos² ( 9 bv - ^a vn ) ) ,

  
  

  где s — величина обратная скачку плотности газа на фронте УВ. В случае магнитной газодинамики s = s (y, M A , M s , a vn , Э ьп ), где a vn и $ bn — углы между нормалью к УВ и направлением потока плазмы или магнитного поля соответственно. Кубическое уравнение для определения s получено в работе [Petrinec, Russell, 1997, уравнение (12)]. Угол отклонения (скошенности) зависит от угла 9 _bv между направлениями ММП и потока солнечного ветра, альфвеновского М _А и звукового М _S чисел Маха. Эффект исчезает для течений с магнитным полем, параллельным или перпендикулярным потоку. Для типичных условий в околоземном солнечном ветре угол отклонения потока составляет ~5° и может достигать 20°–30° при малых М A .

МЕТОДИКА АППРОКСИМАЦИИ ОКОЛОПЛАНЕТНОЙ УВ

АНАЛИТИЧЕСКИМ

ВЫРАЖЕНИЕМ

При построении аналитической модели околопланетной УВ для случаев, когда ММП параллельно или перпендикулярно набегающему потоку плазмы, Котова и др. [2020] использовали следующее выражение для описания ее формы и положения:

Р^{2 (} x ) = ² R s ⁽ r s - x ) +

⁺ tg²® as ⁽ r s - x ⁾²

(

1 +

b s tg²ω_as

- 1

1 + d s

r s - х

V

R

где ρ=(y2+z2)1/2; rs — расстояние до УВ в подсолнечной (носовой) точке; Rs — радиус кривизны; bs — затупленность УВ в носовой точке; ωas — асимптотический наклон УВ, определяющий асимптотическое число Маха Mas= 1/sin2 ωas. Затупленность — безразмерный параметр, характеризующий форму УВ. Носовая часть УВ близка по форме к сплюснутому эллипсоиду при bs<–1 и к вытянутому эллипсоиду при –10. Параметр ds характеризует переход от доминирования параметров подсолнечной области УВ к доминированию параметров области, где основную роль играет асимптотический наклон УВ. При произвольном направлении ММП форма УВ имеет единственную симметрию относительно плоскости XY, содержащей векторы ММП и скорости набегающего потока, и параметры выражения (2), кроме rs, зависят от часового угла φ. В таком общем случае УВ нужно рассматривать в системе координат, в которой оси Xs и Ys повернуты на угол αvn от осей XGIPM и YGIPM по часовой стрелке. В этой повернутой на угол скошенности системе координат также удается получить точное аналитическое решение МГД-уравнений для ωas при произвольном угле ϑbv [Verigin et al., 2003b], а для аппроксимации УВ по-прежнему можно использовать выражение (2).

В случае когда вектор магнитного поля перпен- дикулярен вектору скорости потока, для радиуса кривизны и затупленности использовались выражения [Котова и др., 2020]:

^R sy ^R sz

R s (φ) =

,

R sin²φ + R cos²φ sy                 sz

bs(φ) =bszsin2φ+bsycos2φ, где Rsy, Rsz — радиусы кривизны, а bsy, bsz — затуп-ленности в подсолнечной точке поверхности ударной волны в плоскостях XY, т. е. при φ=0°, и XZ, т. е. при φ=90°, соответственно. Будем использовать эти выражения и для произвольного направления ММП. Параметр ds пока будем считать не зависящим от φ.

Итак, для аппроксимации поверхности УВ выражением (2) нужно подобрать семь параметров:

α vn ,

b sz , d s .

r s , R sy , R sz ,

b sy ,

На рис. 1 показан пример аппроксимации рас- считанной в МГД-приближении УВ около сфериче- ски-цилиндрического   препятствия. Параметры аппроксимации: αvn=4.0°, rs=1.33, Rsy=1.79, Rsz=1.82, bsy=–0.33, bsz=–0.14, ds=1.05. Видно хорошее согласие аналитической аппроксимации с МГД-расчетами.

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ АНАЛИТИЧЕСКОЙ

МГД-АППРОКСИМАЦИИ УВ ПО ГД-РАСЧЕТАМ

Для того чтобы найти общие выражения для параметров аппроксимации, будем использовать газодинамическую аналитическую модель УВ, которая весьма точно описывает ее положение около препятствий различной формы [Verigin et al., 2003a] . Формулы для расчета ГД-параметров приведены в приложении 1. В работе [Котова и др., 2020] получены формулы для пересчета ГД-параметров в МГД для течений с магнитным полем, параллельным или перпендикулярным потоку плазмы. В эти формулы входит дополнительный фактор Г , возникающий при рассмотрении расширения центральной трубки тока за УВ для МГД-течения по сравнению с ГД-течением. В случае ГД-течения относительный темп расширения центральной трубки тока описывается следующим уравнением:

1 dS 21 - ε 1 d (ρ V ) =-=    .

S dx   R _s ερ V dx

Для МГД-течения это выражение можно записать таким образом:

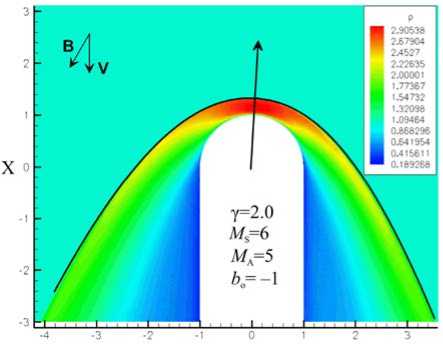
Рис. 1 . Положение и форма УВ (в плоскости X_GIPMY_GIPM), образующейся в набегающем потоке солнечного ветра с магнитным полем, направленным под углом 30° к скорости потока. Утолщенная линия — аппроксимация с помощью (2). Длинной стрелкой показано направление нормали к УВ в носовой точке

1 dS    R sy + R sz 1 - ε1

=-

S dx R R ε Г sy sz где Γ=Γ(ε, γ, MA, MS, ϑbv, αvn); γ — показатель политропы (см. приложение 2). При расчете МГД-парамет-ров rs, Rs, bs за основу берем те же формулы из [Verigin et al., 2003a], но с рассчитанным в МГД-приближении параметром сжатия ε и с заменой ε*=ε/(ε–1) на ε*Г и MS на Mas=(1+1/tg2 ω)1/2.

Рисунок 2, a демонстрирует, что при любом направлении магнитного поля для определения расстояния до носовой точки УВ r s norm можно использовать формулу, полученную в работе [Котова и др., 2020] :

r - r = Г ^2/3 × s norm o

× ( r _{s GD} (( Г ε/(1 - ε), γ, R _o, b _o) - r _o)χ( ϑ _bv),

χ(ϑbv)=1+0.37sinϑbv, где Ro — радиус кривизны; bo — затупленность препятствия в подсолнечной точке, rs — расстояние до носовой точки УВ, рассчитанное в ГД-приближении с заменой ε* на Γε* [Verigin et al., 2003a]. Аналогично формулы для радиусов кривизны поверхности УВ вблизи носовой точки совпадают c теми, которые были получены ранее для частных случаев направлений ММП:

R = Г sy norm =

-

2/3RsGD(εГ, γ, Ro, bo)(Masy/Masz)1/2, sinϑbv/2 sz = sy            , где асимптотические числа Маха в направлениях y и z:

M ² asy

M ² asz

1 tg2(ωy)

1 tg2(ωz)

+ 1,

+ 1.

Для пересчета ГД-параметров b s и d s в соответствующие МГД-параметры пока получены только предварительные соотношения.

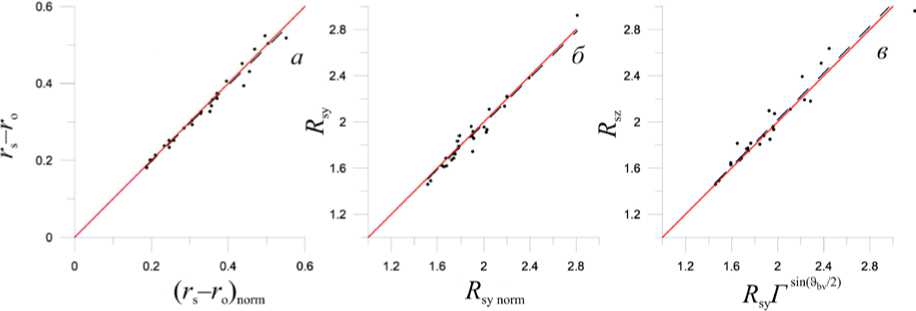
Рис. 2. Сравнение параметров модели ударной волны (2), аппроксимирующей результаты МГД-расчетов, с параметрами ГД-модели (приложение 1)

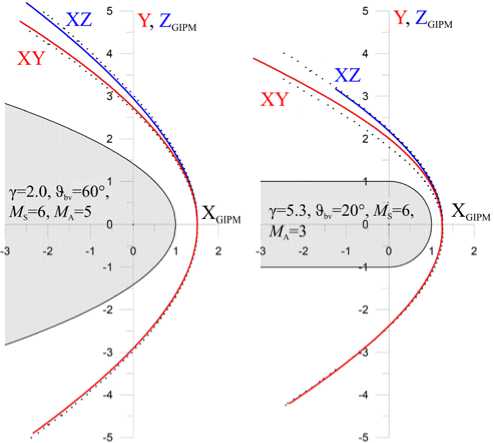
Рис. 3 . Положение и форма УВ, образующейся около двух различных препятствий в плоскостях XY и XZ: точки — МГД-расчет; сплошные линии — аппроксимация (2) с параметрами, пересчитанными по ГД-формулам

На рис. 3 показаны два примера положения и формы ударной волны, определенных с помощью перенормированных ГД-формул ( b s и d s пересчитывались по формулам для случая магнитного поля, перпендикулярного направлению потока плазмы [Котова и др., 2020] ).

ВЫВОДЫ

Присутствие межпланетного магнитного поля в потоке солнечного ветра приводит к дополнительному отклонению носовой части ударной волны от аберрированной оси X в плоскости XGIPMYGIPM системы координат GIPM. Показано, что для любого направления вектора магнитного поля относительно вектора скорости потока плазмы поверхность околопланетной ударной волны можно аппроксимировать аналитической функцией с помощью четырех– семи свободных параметров, имеющих ясный физический смысл: расстояния до носовой точки, радиусов кривизны и затупленности в носовой точке в плоскостях XY и XZ, параметра перехода к асимптотическому углу наклона и угла скошенности. Параметры можно пересчитать в газодинамическом приближении.