Аналитическая оценка частоты собственных колебаний плоской решетки
Автор: Кирсанов М.Н.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 4 т.22, 2022 года.
Бесплатный доступ
Введение. Предлагается новая схема плоской статически определимой регулярной решетки. Стержни решетки соединены шарнирами. Цель исследования - вывести формулу зависимости от числа панелей первой частоты собственных колебаний узлов, наделенных массами, каждая из которых имеет две степени свободы в плоскости решетки. Жесткость всех стержней принята одинаковой, опоры (подвижный и неподвижный шарниры) недеформируемыми. Другая цель исследования - найти в аналитической форме зависимость усилий в наиболее сжатых и растянутых стержнях от числа панелей. Материалы и методы. Используется приближенный метод Донкерлея определения нижней оценки собственной частоты колебаний решетки. Жесткость решетки находится в аналитической форме по формуле Максвелла - Мора. Усилия в стержнях и реакции опор определяются из уравнений равновесия, составленных для всех узлов решетки. Обобщение результата на произвольное число панелей выполняется методом индукции с применением операторов символьной математики Maple по аналитическим решениям ряда задач для решеток с различным числом панелей. Результаты исследования. Нижняя аналитическая оценка первой частоты колебаний хорошо согласуется с численным решением для минимальной частоты спектра колебаний конструкции. Найдены формулы для усилий в четырех наиболее сжатых и растянутых стержнях и их линейные асимптотики. Все необходимые преобразования производятся в системе символьной математики Maple. Обсуждение и заключения. Полученная зависимость первой частоты колебаний решетки от числа панелей, массы и размеров конструкции имеет компактную форму и может быть использована как тестовая задача для численных решений и при оптимизации конструкции.
Решетка, собственная частота, оценка донкерлея, индукция, формула максвелла-мора, maple, нижняя оценка частоты, аналитическое решение, усилия в стержнях, асимптотика
Короткий адрес: https://sciup.org/142236327
IDR: 142236327 | УДК: 624.04:531.391.3 | DOI: 10.23947/2687-1653-2022-22-4-315-322
Текст научной статьи Аналитическая оценка частоты собственных колебаний плоской решетки
Введение. Предлагается новая схема плоской статически определимой регулярной решетки. Стержни решетки соединены шарнирами. Цель исследования — вывести формулу зависимости от числа панелей первой частоты собственных колебаний узлов, наделенных массами, каждая из которых имеет две степени свободы в плоскости решетки. Жесткость всех стержней принята одинаковой, опоры (подвижный и неподвижный шарниры) неде-формируемыми. Другая цель исследования — найти в аналитической форме зависимость усилий в наиболее сжатых и растянутых стержнях от числа панелей.
Материалы и методы. Используется приближенный метод Донкерлея определения нижней оценки собственной частоты колебаний решетки. Жесткость решетки находится в аналитической форме по формуле Максвелла — Мора. Усилия в стержнях и реакции опор определяются из уравнений равновесия, составленных для всех узлов решетки. Обобщение результата на произвольное число панелей выполняется методом индукции с применением операторов символьной математики Maple по аналитическим решениям ряда задач для решеток с различным числом панелей.
Результаты исследования. Нижняя аналитическая оценка первой частоты колебаний хорошо согласуется с численным решением для минимальной частоты спектра колебаний конструкции. Найдены формулы для усилий в четырех наиболее сжатых и растянутых стержнях и их линейные асимптотики. Все необходимые преобразования производятся в системе символьной математики Maple.
Обсуждение и заключения. Полученная зависимость первой частоты колебаний решетки от числа панелей, массы и размеров конструкции имеет компактную форму и может быть использована как тестовая задача для численных решений и при оптимизации конструкции.
Машиностроение и машиноведение
Original article
Analytical Estimation of the Natural Oscillation Frequency of a Planar Lattice
M. N. Kirsanov о
National Research University (MPEI), 14, Krasnokazarmennaya St., Moscow, Russian Federation
Introduction. A new scheme of a flat statically determinate regular lattice is proposed. The lattice rods are hinged. The study aims at deriving a formula for the dependence on the number of panels of the first natural oscillation frequency of nodes endowed with masses, each of which has two degrees of freedom in the lattice plane. The rigidity of all rods is assumed to be the same, the supports (movable and fixed hinges) — nondeformable. Another objective of the study is to find the dependence of the stresses in the most compressed and stretched rods on the number of panels in an analytical form.
Materials and Methods. An approximate Dunkerley’s method was used to determine the lower bound for the lattice natural frequency. The lattice rigidity was found in analytical form according to Maxwell-Mohr formula. The rod stresses and the reactions of the supports were determined from the equilibrium equations compiled for all lattice nodes. Generalization of the result to an arbitrary number of panels was performed by induction using Maple symbolic math operators for analytical solutions to a number of problems for lattices with different number of panels.
Results. The lower analytical estimate of the first oscillation frequency was in good agreement with the numerical solution for the minimum frequency of the oscillation spectrum of the structure. Formulas were found for the stresses in four most compressed and stretched rods and their linear asymptotics. All required transformations were made in the system of Maple symbolic math.
Discussion and Conclusions. The obtained dependence of the first frequency of lattice oscillations on the number of panels, mass and dimensions of the structure has a compact form and can be used as a test problem for numerical solutions and optimization of the structure.
Funding information. The research is done with the financial support from RFFI within the frame of research project no. 22–21–00473.
Acknowledgments. The author would like to thank the reviewers, whose critical evaluation of the submissions and suggestions for improvement contributed significantly to the quality of this article.
Введение. Решетчатые конструкции широко применяются в машиностроении как несущие или ограждающие элементы. Методика расчета собственных частот колебаний решетки традиционно базируется на численных расчетах, как правило, использующих метод конечных элементов с применением специализированных пакетов. Значительно реже применяются аналитические методы. Развитие математических пакетов символьной математики (Maple, Wolfram Mathematica, Derive, Maxima и др.) дает возможность искать такие решения для регулярных систем, в которых возможен учет порядка регулярности (числа периодических структур конструкции, например, числа панелей) в решении. Цель исследования — найти аналитическую зависимость нижней границы первой частоты решетчатой конструкции от числа панелей. Зависимость решения от числа панелей значительно расширяет область применения формулы и дает возможность оптимизировать конструкцию по какому-либо параметру. Впервые проблемой существования и расчета статически определимых регулярных стержневых систем занялись Хатчинсон Р. и Флек Н. [1, 2]. В [3, 4] такие конструкции изучались в связи с задачами оптимизации. Существуют также аналитические решения в виде конечных формул для прогибов регулярных плоских [5–7] и пространственных ферм [8]. В справочнике [9] приводятся формулы для прогибов и смещений опор плоских ферм и решеток с произвольным числом панелей. В [10–13] получены нижние оценки первой собственной частоты колебаний плоских ферм, найденные методом индукции для произвольного порядка регулярной конструкции.
Есть другое направление аналитических исследований конструкций [14–16]. В этих работах решение находится в системе Maple в виде тригонометрических рядов.
В настоящей работе используется метод индукции, заключающийся в обобщении ряда отдельных расчетов решеток с последовательно увеличивающимся числом панелей на случай произвольного числа панелей. Во всех преобразованиях используются операторы системы символьной математики Maple. Объектом исследования является новая схема регулярной статически определимой плоской решетки прямоугольного очертания в виде несимметричной фермы на двух опорах. Ставится задача вывести аналитическую зависимость основной частоты колебаний конструкции от числа панелей. Выведенная формула может быть использована в задачах оптимизации и для оценки численных решений подобных конструкций большого порядка, для которых в численных расчетах возможны погрешности, связанные с накоплением ошибок округления.
Материалы и методы. В ферме длиной (2 n - 1) а и высотой 4 h содержится 5( n + 1) узлов, включая и три опорных узла (один для крепления левой опорной стойки, два — для правых стержней, моделирующих неподвижный шарнир). Число стержней, включая три опорных стержня, N = 10 n + 4 . Ферма статически определимая. При расчете частот колебаний конструкции предполагается, что масса фермы сосредоточена в узлах.
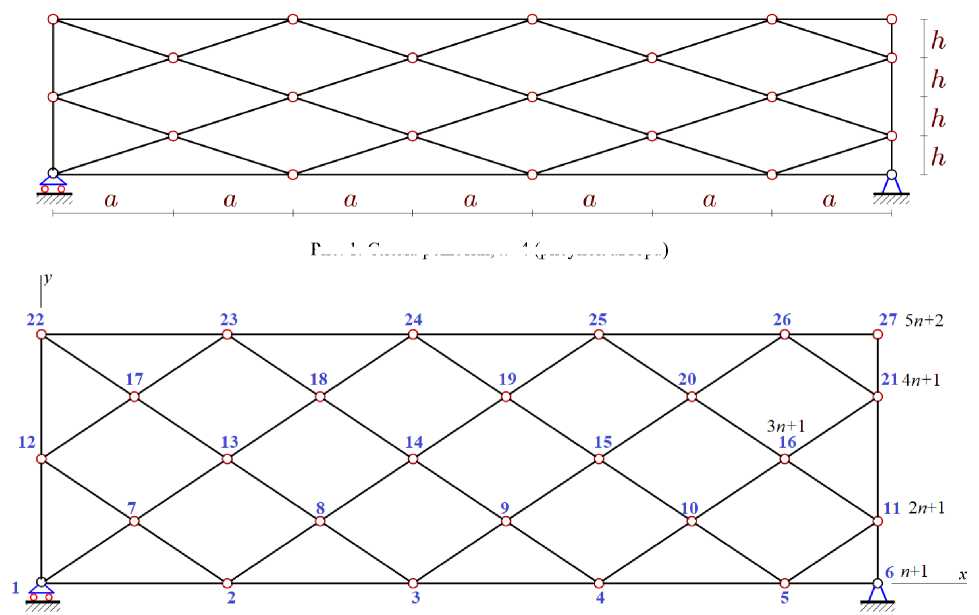
Рис. 1. Схема решетки, n =4 (рисунок автора)
Рис. 2. Нумерация узлов решетки, n =5 (рисунок автора)
Вычисление усилий выполняется в системе Maple по программе [17]. Узлы и стержни фермы нумеруются (рис. 2). Начало координат находится в левой опоре. Координаты задаются в циклах.
Структура решетки устанавливается порядком соединения стержней в узлах. Для этого вводятся специальные списки Фа = [ i , i 2] номеров i , i2 концов стержней а = 1,.., N . Стержни нижнего внешнего контура, например, имеют следующие номера узлов по концам: Ф, = [ i , i + 1], i = 1,.., n. Таким же образом задаются и номера концов остальных стержней решетки. Система уравнений равновесия узлов в проекциях на оси координат составляется в матричном виде GS = B, S — вектор всех усилий в стержнях, включая и три реакции опор, B — вектор внешних узловых нагрузок. Матрица системы G состоит из направляющих косинусов усилий. При этом одно и то же усилие приложено к разным концам стержня и направлено в разные стороны:
G2Ф,2-1,i =-lx,i Ili,G2Ф2,i =-ly,i Ili; i ,2 , , ,2 ,,
G2Ф,1-1,, = ^ 11., G2Ф, „i = ly,i 11., i = 1,-, N, i ,1
где l = хф - хф , l = уф - уф — проекции условных векторов стержней на оси координат;
x,i i,1 i,2 y,i i,1
l = V lx2i + 12i — длина стержня i =1,.., N .
Усилия в стержнях решетки можно получить из решения системы уравнений в символьном или численном виде.
Машиностроение и машиноведение
Результаты исследования. Рассмотрим напряженное состояние решетки в случае нагружения по всем узлам вертикальными силами P (рис. 1). На рис. 3 дана картина распределения усилий в стержнях конструкции. Толщины отрезков на рисунке условно пропорциональны модулям соответствующих усилий. Синим цветом выделены сжатые стержни, красным — растянутые. Значения усилий отнесены к величине P нагрузки на узел с округлением до двух значащих цифр. Наиболее растянутый стержень ожидаемо оказался в середине нижнего пояса, наиболее сжатый — в нижнем стержне на правой боковой стороне конструкции.
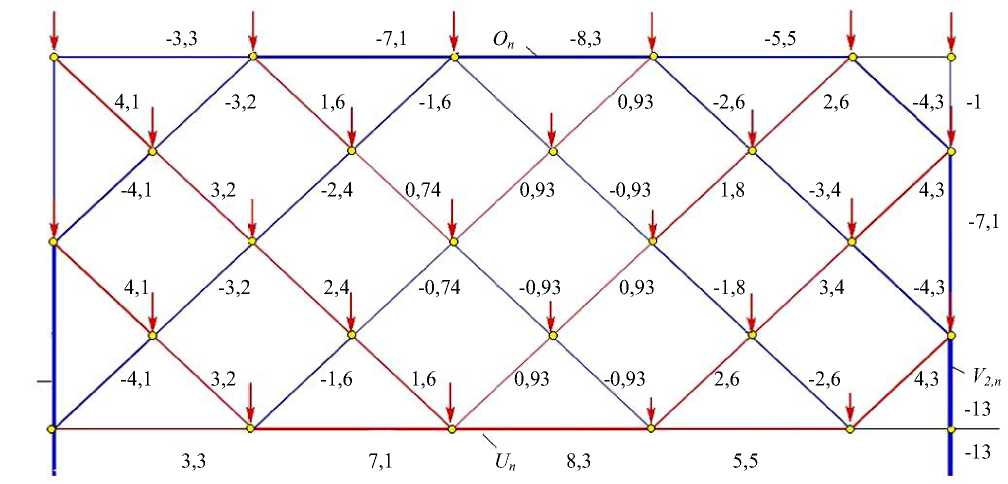
Рис. 3. Распределение усилий по стержням решетки, a=4 м, h=3 м, n=5 (рисунок автора)
Аналитические зависимости усилий в наиболее сжатых и растянутых стержнях от числа панелей получаются методом индукции из обобщения последовательностей отдельных решений. Например, для усилия V ив нижнем стержне левой стороны решетки последовательность значений для решеток порядка n = 1, 2, 3, ... имеет вид: V/ P= -2, -12, -28, -54, -84, -126, -170, - 228, - 286, -360,.... Рекуррентное уравнение для об щего члена этой последовательности дает оператор rgf_findrecur системы Maple:
V 1, n = V 1, n - 1 + 2 V 1, n - 2 - 2 V 1, n - 3 - V 1, n - 4 + V 1, n - 5.
Решение уравнения с помощью оператора rsolve:
V 1, n = - P (30 n 2 - 2(7 - ( - 1) n ) n - ( - 1) n + 1) /(8(2 n - 1)) .
Таким же образом находятся и другие выражения для критических усилий:
O = - Pa (20 n 3 - 30 n 2 + 5 - 4(cos ϕ + sin ϕ )(1 - 2 n ) - cos(2 ϕ )) / (32(2 n - 1) h ); U =- O ;
V2,n = -P(5n2- n -1) /(2n -1),
где ϕ = π n /2. Интересно заметить, что усилия V и V не зависят от размеров a и h .
Аналитическая форма решений позволяет найти их асимптотики с помощью оператора limit системы Maple: limV1n = -3Psum/8, limV2n = -3Psum/8; n→∞ , n→∞ , limOn /n=-limUn /n = -aPsum / (16h), n→∞ n→∞ где P = 5nP — суммарная нагрузка на решетку. Для усилий V и V в стержнях на боковых сторонах ре шетки асимптоты горизонтальные, для усилий O и U на верхнем и нижнем поясах — наклонные.
Частота собственных колебаний . Из всего спектра частот собственных колебаний конструкции для оценки ее динамического поведения наиболее важной является первая, низшая, частота. Ее значение входит в большинство решений задач динамики конструкции. Эта величина требуется в том числе и для оценки сейсмических характеристик сооружения. Нижнюю границу первой частоты для регулярных конструкций в форме зависимости от числа панелей можно получить аналитически.
При определении собственных частот колебаний конструкции принята упрощенная модель инерционных свойств фермы. Предполагается, что стержни решетки не имеют массы, а вся масса распределена равномерно по узлам. Пренебрегая движением опор, получаем общее число степеней свободы равное K = 10 n . Формула Донкерлея [13] для оценки нижней границы первой частоты имеет вид:
K
®"D = Ё ю-2,(1)
р = 1
где top — парциальные частоты конструкции. Парциальные частоты колебаний масс определяются из уравнения:
тУр + DpVp = 0, Р =1,-,K(3)
Здесь ур = yp (t ) — координата узла p; у — ускорение; Dp — жесткость, величина обратная податливости 5р = 1 / Dp . Податливость можно вычислить по формуле Максвелла-Мора:
NU/.х2
5р = 1/Dp = £(5ар)) l«КEF),(4)
а = 1
где 5(р) — усилие в стержне с номером а от действия вертикальной единичной силы, приложенной к узлу р, где расположена масса. Коэффициент жесткости и парциальная частота зависят от места, где расположена масса. Для гармонических колебаний ур = Up sin(tot + ф) из (3) следует top = ^Dp / т. Подстановка этого выражения в (4) дает формулу для оценки первой частоты только по парциальным частотам колебаний масс: KK toD2 = Ё to-2 = т Ё 5 р = m(A n, v + A n, h). (5)
р = 1 р = 1
Отдельно выделены суммы для колебаний по вертикальному направлению An v и горизонтальному An h .
Последовательный расчет частот колебаний решеток различного порядка показывает, что коэффициент An v в (5) имеет вид:
A 1, v = (14 h )/( EF );
A2 „ = (44 a 3 + 75 c 3 + 250 h 3) / (9 EFh 2);
A3v = (24 a 3 + 25 c 3 + 36 h 3)/( EFh 2);
A4v = 2(154 a 3 + 175 c 3 + 176 h 3)/(7 EFh 2);
A5 „ = 2(1254 a 3 + 1125 c 3 + 791 h 3) / (27 EFh 2).
В общем случае для парциальных частот по вертикали:
A n , v = ( C a 3 + C c 3 + C 3 y h 3 ) / ( EFh 2 ) . (6)
Для парциальных частот по горизонтали:
Машиностроение и машиноведение
A n , v = ( C 4 a 3 + C 5 c 3 + C y h 3 ) / ( EFa 2 ) . (7)
Используя оператор rgf_findrecur системы Maple, получаем однородное рекуррентное уравнение седьмого порядка для определения коэффициента при a 3 :
C n = 3CX ,n - 1 - C n - 2 - 5CV n - 3 + C n _ 4 + C n - 5 - 3 C 1, n - 6 + C n - 7 .
Решение уравнения дает оператор rsolve:
C = ( n 4 - 2 n 3 + 61 n 2 - 6(3( - 1) n + 10) n + 9( - 1) n - 9)/18. (8)
Таким же образом находятся и другие коэффициенты:
C = 25 n ( n - 1)/6;
2 2 (9)
C = (136 n 2 + 2(9( - 1) n - 14) n - 9( - 1) n - 15)/(6(2 n - 1)).
Аналогично:
C 4 = (164 n 3 - (36cos(2 ф ) + 142) n 2 + (24cos(2 ф ) - 24sin ф + 24cos ф + 20) n -
- 3 cos(2 ф ) + 12sin ф - 12cos ф + 27) / (2 n - 1) /12;
C5 = (10 n 3 - 5 n 2 + 15 n + 8)/(2(2 n - 1)); (10)
C 6 = (3 6 n 3 - (2 8 + 8cos(2 ф )) n 2 + (128 + 22cos(2 ф ) + 24cos ф- 24sin ф ) n -- 12cos ф- 9cos(2 ф ) + 109 + 12sin ф ) / (2 n - 1)2 /2, где ф = n n /2.
В результате из (5–7) следует выражение для нижней оценки первой частоты:
to- 2 = m ( ( Cxa 3 + Сгс 3 + Ch 3 ) / h 2 + ( C4a 3 + C5c 3 + C6h 3 ) / a 2 ) / ( EF ). (11)
с коэффициентами (8), (9) и (10).
Оценка погрешности решения (11) возможна из сравнения с минимальной частотой всего спектра собственных частот решетки, полученной численно. Спектр системы с многими степенями свободы находится из решения задачи о собственных числах матрицы. Дифференциальные уравнения динамики масс конструкции с числом степеней свободы K записываются в матричном виде:
mIKY + D^Y = 0, (12)
где D — матрица жесткости фермы; Y — вектор смещений масс; I — единичная матрица. Пусть B — матрица, обратная D . Умножение (12) слева на B , дает уравнение:
m B^Y + LY = 0. (13)
KK
Связь Y = -to 2Y справедлива для гармонических колебаний с частотой го. Отсюда из (13) следует задача о собственных значениях: B^ Y = X Y, где X = 1/ (го2 m ) — собственные значения матрицы Бх. Элементы матрицы податливости находятся по формуле Максвелла-Мора. Для вычисления собственных значений матрицы в системе Maple предназначен оператор Eigenvalues из пакета линейной алгебры LinearAlgebra. Решение этой задачи в общем случае можно получить только в численной форме.
Пример. Стальная решетка имеет длину панели a = 2 м, высоту h = 1 м, массы в узлах m = 300 кг , жесткость стержней EF = 0,8 - 10 5 кН . На рис. 4 показаны зависимости первой частоты от числа панелей, полученные численно и аналитически.
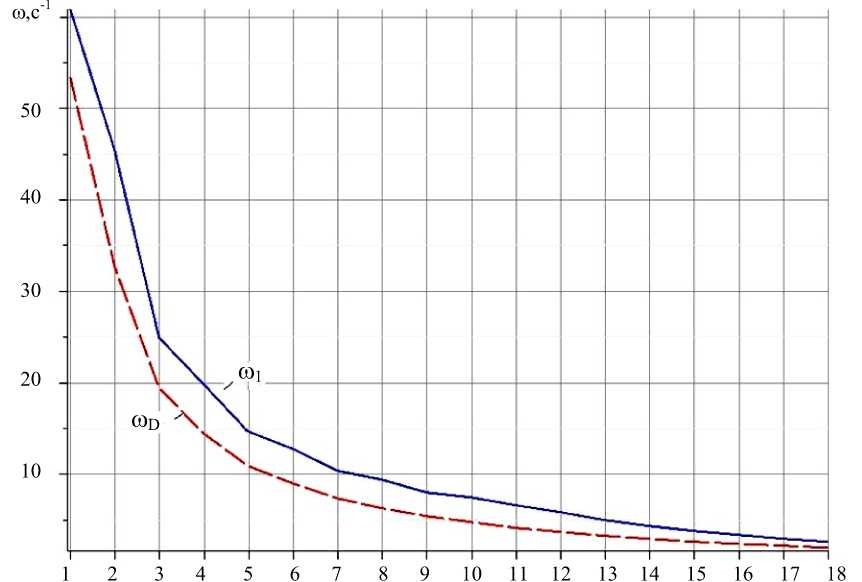
Рис. 4. Сравнение первой частоты собственных колебаний решетки rot и ее нижней аналитической оценки roD в зависимости от числа панелей (рисунок автора)
Относительная погрешность е = ^ - ю£))/го1, в зависимости от числа панелей (рис. 5), показывает, что с увеличением числа панелей погрешность, начиная с n =1, растет, а затем монотонно и достаточно быстро убывает. Это особенно важно при использовании полученной формулы при расчете решеток с большим числом панелей, для которых численный счет начинает набирать погрешность, связанную с накоплением ошибок
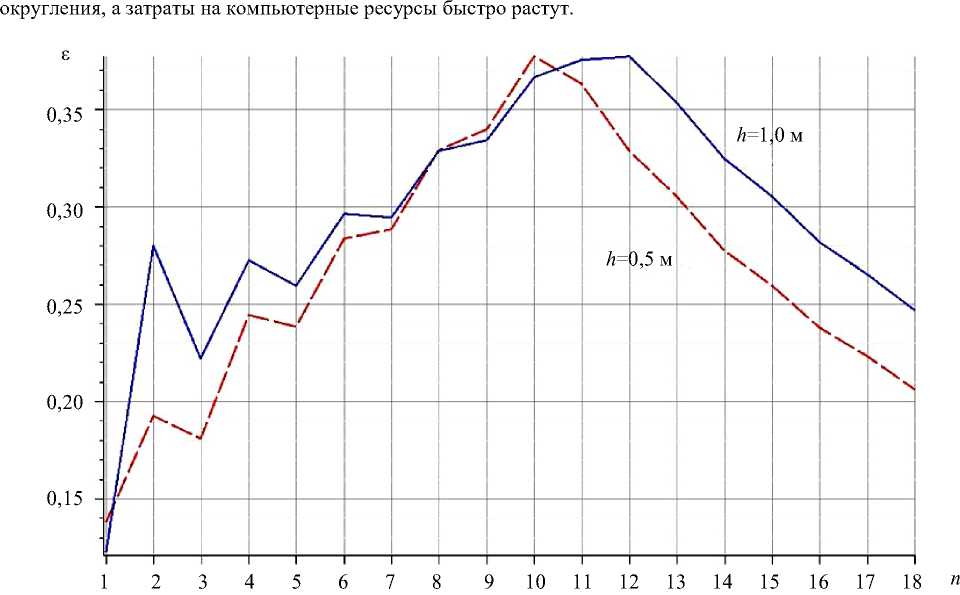
Рис. 5. Погрешность аналитического решения для собственной частоты в зависимости от числа панелей и высоты h (рисунок автора)
Обсуждение и заключения. Предложена схема статически определимой плоской решетки. Поставлена задача получить аналитическое выражение нижней границы первой частоты собственных колебаний решетчатой фермы для произвольного числа панелей в конструкции. Решение получено методом индукции в системе Maple. Наличие экстремумов на построенных кривых дает возможность оптимизировать число панелей решетки, выбрав наибольшую точность оценки и подобрав требуемую частоту колебаний. В предложенном исследовании учтены горизонтальные колебания масс. Учет горизонтальных колебаний несколько усложняет итоговую расчетную формулу, делая ее более громоздкой. Помимо использованного метода Донкерлея, для оценки первой частоты есть более точный энергетический метод Рэлея, дающий оценку первой частоты сверху. Однако и это решение в рассматриваемом случае имеет излишне громоздкий вид и здесь не приводится.
Список литературы Аналитическая оценка частоты собственных колебаний плоской решетки
- Hutchinson, R. G. Microarchitectured Cellular Solids — the Hunt for Statically Determinate Periodic Trusses / R. G. Hutchinson, N. A. Fleck // ZAMM Journal for Applied Mathematics and Mechanics. — 2005. — Vol. 85. — P. 607-617. https://doi.org/10.1002/zamm.200410208
- Hutchinson, R. G. The Structural Performance of the Periodic Truss / R. G. Hutchinson, N. A. Fleck // Journal of the Mechanics and Physics of Solids. — 2006. — Vol. 54. — P. 756-782. https://doi.org/10.1016/JJMPS.2005.10.008 §
- Kaveh, A. Optimal Analysis of Structures by Concepts of Symmetry and Regularity / A. Kaveh. — Vienna : o Springer, 2013. — 463 p. https://doi.org/10.1007/978-3-7091-1565-7 £
- Kaveh, A. Truss Optimization with Natural Frequency Constraints Using a Hybridized CSS-BBBC Algorithm g with Trap Recognition Capability / A. Kaveh, A. Zolghadr // Computers & Structures. — 2012. — Vol. 102-103. — | P. 14-27. https://doi.org/10.1016J.C0MPSTRUC.2012.03.016
- Ovsyannikova, V. M. Dependence of Deformations of a Trapezous Truss Beam on the Number of Panels / ^ V. M. Ovsyannikova // Structural Mechanics and Structures. — 2020. — Vol. 3 (26). — P. 13-20.
- Ilyushin, A. S. The Formula for Calculating the Deflection of a Cmpound Externally Statically Indeterminate Frame / A. S. Ilyushin // Structural Mechanics and Structures. — 2019. — Vol. 22. — P. 29-38.
- Qiao Dai. Analytical Dependence of Planar Truss Deformations on the Number of Panels / Qiao Dai // AlfaBuild. — 2021. — Vol. 17. — P. 1701. 10.34910/ALF.17.1
- Kirsanov, M. N. The Stress-Strain State of a Rectangular Covering Spatial Truss / M. N. Kirsanov // Construction of Unique Buildings and Structures. — 2020. — Vol. 91. — P. 9104.
- Kirsanov, M. Trussed Frames and Arches: Schemes and Formulas / M. Kirsanov. — UK : Cambridge Scholars Publishing Lady Stephenson Library, 2020. — 178 p.
- Petrichenko, E. A. Lower Bound of the Natural Oscillation Frequency of the Fink Truss / E. A. Petrichenko // Structural Mechanics and Structures. — 2020. — Vol. 3 (26). — P. 21-29.
- Petrenko, V. F. The Natural Frequency of a Two-Span Truss / V. F. Petrenko // AlfaBuild. — 2021. — Vol. 20. — P. 2001.
- Vorobev, O. V. Bilateral Analytical Estimation of the First Frequency of a Plane Truss / O. V. Vorobev // Construction of Unique Buildings and Structures. — 2020. — Vol. 92. — P. 9204.
- Vorobyev, O. About Methods of Obtaining Analytical Solution for Eigenfrequencies Problem of Trusses / O. Vorobyev // Structural Mechanics and Structures. — 2020. — Vol. 24. — P. 25-38.
- Goloskokov, D. P. Approximate Analytical Solutions in the Analysis of Thin Elastic Plates / D. P. Goloskokov, A. V. Matrosov // AIP Conference Proceedings. — 2018. — Vol. 1959. — Art. 070012. 10.1063/1.5034687
- Goloskokov, D. P. Approximate Analytical Approach in Analyzing an Orthotopic Rectangular Plate with a Crack / D. P. Goloskokov, A. V. Matrosov // Materials Physics and Mechanics. — 2018. — Vol. 36. — P. 137-141.
- Goloskokov, D. P. Comparison of Two Analytical Approaches to the Analysis of Grillages / D. P. Goloskokov, A. V. Matrosov // In: Proc. 2015 Int. Conf. "Stability and Control Processes" in Memory of V. I. Zubov (SCP). — 2015. — P. 382-385. 10.1109/SCP.2015.7342169
- Buka-Vaivade, K. Calculation of Deformations of a Cantilever-Frame Planar Truss Model with an Arbitrary Number of Panels / K. Buka-Vaivade, M. N. Kirsanov, D. O. Serdjuks // Vestnik MGSU. — 2020. — Vol. 15. — P. 510-517. 10.22227/1997-0935.2020.4.510-517


