Аналитическая система информационного обеспечения дискретных процессов управления на основе компактных сетевых моделей

Как уже отмечалось в работе [6] известные на сегодняшний день сетевые модели для моделирования элементарных процессов имеют существенный недостаток: они являются «массивными», это обусловлено тем, что в состав моделей входит большое количество различных компонент. С этой целью в работе [6] была поставлена и частично решена задача разработки новых моделей и методики, которые обеспечили более компактное моделирование, за счет построения компактной сетевой модели.

Модели элементарных процессов

Базовые графы с приоритетами - это модели ЭП, которые взаимодействуют между собой на различных уровнях иерархии, тем самым образуя ИП [2]. Графом элементарного процесса (ГЭП) модели M(p) называется ориентированный граф G(p), который обладает следующими свойствами: 1) число вершин графа G(p) равно числу состояний ЭП p, причем между вершинами G(p) и состояниями p имеется взаимно однозначное соответствие; 2) число дуг графа G(p) равно числу переходов ЭП p между дугами и переходами также существует взаимно однозначное соответствие. При этом переходам первого порядка соответствуют петлевые дуги или дуги первого рода, а переходам второго порядка - непетлевые дуги или дуги второго порядка; 3) дуги исходящие из каждой вершины графа G(p) упорядочены в последовательности по убыванию приоритетов соответствующих переходов. Число равное порядковому номеру дуги в данной последовательности, называется приоритетом дуги; 4) каждой дуге d графа G(p) поставлен в соответствии свой предикат активности Pa(p). Дуга называется активной в некоторый момент времени t, если ее предикат активности равен единице; 5) каждой дуге d графа G(p) соответствует некоторый символ алфавита S, включающего пустой символ S0. Начальной вершиной M(p) является вершина s0 графа G(p), соответствующая начальному состоянию p.

Соответствие дуг и вершин

Для построения так называемой компактной модели на основе ранее описанных моделей элементарных процессов необходимо обозначить понятия соответствующих дуг и вершин.

Для двух различных ГЭП две рассматриваемые вершины являются соответствующими, если это либо начальные вершины двух ГЭП, либо вершины, в которые ведут соответствующие дуги.

Дуги двух различных ГЭП являются соответствующими, если эти дуги исходят из соответствующих вершин, причем для вершины, в которую ведет каждая из этих дуг, не существует соответствующей, отличной от той, в которую ведет другая дуга, и для любой из этих дуг не существует соответствующей, отличной от другой дуги [5].

Таким образом, для любой вершины или дуги одного ГЭП не существует более одной соответствующей вершины и дуги другого ГЭП.

Компактная сетевая модель

На основании моделей M(p) строится компактная сетевая модель M(p)k. Данная модель в дальнейшем может быть использована для контроля развития ЭП вместо нескольких моделей различных процессов, то есть компактная сетевая модель будет эквивалента ранее объединенным моделям. Компактная сетевая модель включает в себя следующие компоненты:

• а)    предикат активности p k = V NL1 p ^ , где p i - предикат активности модели ЭП M^p, а V - символ логической операции «ИЛИ». В момент времени t значение предиката активности определяется, как p k = V NL1 p i (t), т.е. процесс, описанный компактной сетевой моделью M^k считается активным, если i-активен хотя бы один процесс, описанной моделью ЭП M p .

• б)    вектор активности, представляет собой вектор-строку вида:

Й = // p a ; p i ; p 3 ; • ••; p a ; • ••; p N /Z N , причем в момент времени t :

p^ t) = // p i (t); p a (t); p 3 (t); —; p i (t); —; p N (t) Z/ N Следовательно, значение вектора активности в каждый текущий момент времени указывает на i-активность процесса по каждой из моделей M^p;

• в)    компактный граф элементарного процесса (КГЭП) - это граф ЭП G^k, включающий начальную вершину a^k = o(G^k), вершины S^k которого (S^k с O k = O(G^k), j =1,..., N^k, N^k = N(G^k)) соединены дугами d k (d k с A^k= A(G^k), l =1,_, H^k, H^k = H(G^k)).

• г)    функция развития m^k.

• д)    функция информационного сопровождения e^k.

При этом для каждой дуги на КГЭП задаются:

• 1)    предикат активности P a (d k ,G^k), который определяет активность дуги;

• 2)    функция прообраза V (d k , G^k, G i ), которая принимает единичное значение, если для дуги d^k КГЭП G^k на ГЭП G i найдется прообраз, т.е. соответствующая ей дуга d (3d (d с A(G i ));

• 3)    вектор-приоритет ^Й (d k ,G^k), который хранит приоритеты всех дуг

d на различных ГЭП, соответствующих d k ;

• 4)    вектор сообщений для оператора "^ (d k , G k ), который хранит символы сообщений таких дуг.

Процедура построения компактной модели основывается на следующих принципах: 1) каждая вершина/дуга КГЭП соответствует некоторой вершине/дуге хотя бы одного из объединяемых ГЭП; 2) все соответствующие друг другу вершины/дуги различных ГЭП соответствуют ровно одной вершине/дуге КГЭП.

Построение обобщенной модели происходит шагами, на каждом из которых строится новый последующий уровень вершин и дуг КГЭП. Входными данными на каждом шаге k являются: а) компактный граф G j—1 , который является подграфом КГЭП G^k (еще недостроенный компактный граф) и сформированный на предыдущем шаге j-1;

• б)    множество всех ГЭП {G i }, i= 1,^,N;

• в)    множество обрабатываемых вершин данных ГЭП O -_—1 (O j_—1 с O i ) с предыдущего шага j-1.

Выходными данными являются:

• а)    граф G _j ^k ;

• б)    множества вершин ГЭП O _j ⁱ .

Для первого шага все начальные вершины являются соответствующими друг другу.

Об использовании компактной сетевой модели

Процедура, предложенная в настоящей работе, позволяет обеспечить безызбыточное хранение моделей различных элементарных процессов в форме компактной сетевой модели при размещении ее в БД.

В качестве реализации построения компактной сетевой модели была предложена аналитическая система, позволяющая автоматически строить КГЭП на основании введенных данных элементарных процессов (рисунок

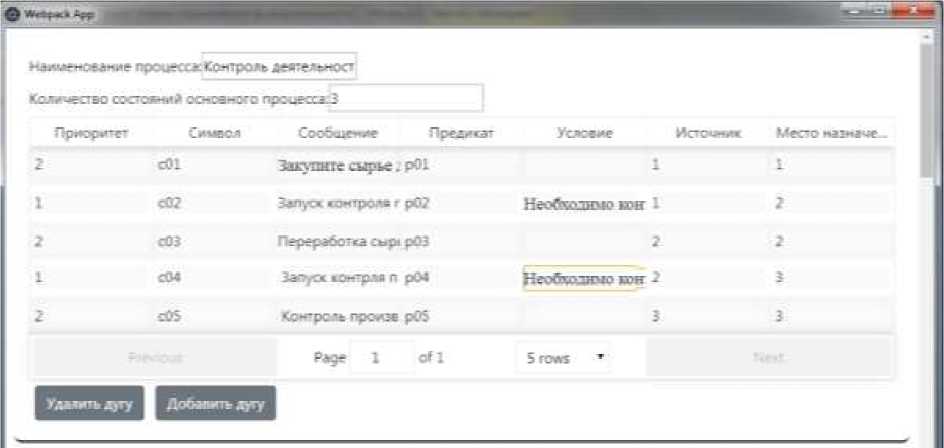
Рисунок 1 – Аналитическая система

Заключение

В настоящей работе предлагается компактная сетевая модель для объединения различных элементарных процессов, которая позволит более компактно представлять данные элементарных процессов.

Очевидно, что для контроля деятельности также необходима процедура восстановления из КГЭП любого ГЭП, которая будет рассмотрена в рамках дальнейших исследований.