Аналитические структуры электрических обобщенно-однородных спектрографических сред

Спектрографическими электронно-оптическими средами мы будем называть электрические поля особой структуры, обладающие свойством пространственно разделять электронные или ионные потоки на систему изоэнергетических струй, сфокусированных на плоский либо прямолинейный позиционно-чувствительный детектор (ПЧД) [1].

Такой способ фиксации энергетических спектров одновременно в большом диапазоне изменения энергий имеет большие преимущества по сравнению с последовательным процессом измерения энергий, который лежит в основе работы большинства традиционных электронных спектрометров. В частности, спектрографы незаменимы при исследовании быстропротекающих физических и химических процессов на поверхности эмиттера (образца) средствами электронной спектроскопии. Идеальную спектрографическую среду образуют поля с потенциалом φ , однородным по Л. Эйлеру. Они характеризуются функциональным тождеством [2]

Ф ( kx,ky,kz ) = к^пф ( x,y,z ) . (1)

В таких полях действует специальный принцип механического подобия, который как раз и обеспечивает струйное разделение потока, причем струи оказываются взаимно подобными, а сфокусированные пятна разной энергии распределяются вдоль луча, проходящего через начало координат x= y = z = 0 — центр гомотетии. Теория таких сред, включающая задачу Коши для симметричных потенциалов, построена в наших работах [3, 4] при помощи комплексных потенциалов Донкина общего вида, что позволило строить широкое многообразие нужных потенциалов с элементарным представлением, выводящее далеко за пределы стандартной теории сферических функций [5]. Этот прием в литературе не встречается. В данной работе мы распространяем наши методы на класс трехмерных потенциалов, которые удобно назвать обобщенно-однородными. Их форма такова ф (x,y,z) = P (x,y,z) ln^ (x,y,z) + Q (x,y,z). (2)

Здесь P , Q — однородные функции одинаковой кратности n , а R — однородная функция кратности m . Числа m и n могут быть любыми вещественными, но мы предпочтем только целые числа, положительные и отрицательные, включая 0. В классе этих структур также действует принцип подобия, но не абсолютно точный, а с некоторыми искажениями, что, впрочем, не мешает синтезировать на их базе весьма эффективные спектрографы [6]. К сожалению, потенциалы типа (2) за редчайшим исключением не позволяют проинтегрировать уравнения движения в замкнутой аналитической форме, и здесь приходится полагаться на компьютерное моделирование. Оно позволило выявить скрытую природу движения, в которой замаскированы правила подобия, столь ярко видные в случае чисто однородных полей. В работе [7] мы построили подкласс потенциалов типа (2), обладающих осевой симметрией вида

Ф ( r,z ) = P ( r,z ) ln r + Q ( r,z ) , (3) где r = x ² + y ² , z — цилиндрические координаты, а P , Q — однородные полиномы. Потенциалы (3) удовлетворяют осесимметричному уравнению Лапласа

1 д  д ф  д ² ф   .

. r +   ₂ = 0.

r д r д r    д z ²

Множитель P сам является гармонической функцией, как и In r , но функция Q ( r,z ) заведомо не гармоническая и к ней можно "подмешивать" гармонический полином той же кратности n . Это свойство позволяет расширить класс (3). Он оказался чрезвычайно эффективен в поиске осесимметричных спектрографических сред с высоким качеством фокусировки полых конических пучков с осевой симметрией, но все-таки нужной свободы при постановке обратных задач механики здесь недостает, т. к. в составе потенциала отсутствуют свободные варьируемые функциональные элементы. Задача нашей работы сейчас состоит именно в том, чтобы ввести подобные элементы в общую структуру (2) с помощью все тех же потенциалов Донкина, которые так удачно вплелись в общую теорию однородных по Л. Эйлеру потенциалов [1].

Подчиним структуру (2) трехмерному уравнению Лапласа

.     д ² ф д ² ф д ² ф .

А ф =    +    +    = 0, дx2 ду2 дz2

или в развернутой форме

A P ■ ln R + 2 V P ■V ln R + P ■A ln R + А Q = 0,

„ х д      д       д .

^{где V} = ^j' ⁺^j 2 ⁺^j 3 . д x     д у     д z

Подбирать (конструировать) тройки функций P,Q,R с учетом однородности, обращающие (6) в тождество слишком сложно, и это хочется упростить. Первый шаг в этом направлении состоит в обыгрывании условия Л. Эйлера (1) для однородных функций.

РЕДУКЦИЯ СТРУКТУР (2)

С помощью свойства (1), выбирая подходящий множитель k , нам выгодно привести однородную функцию R ( x,y,z ) к трем типам представления:

R = zm

о [ x у v

■ ⁵ I ■ I;

V z z J

R = r m ■ 5 1-,-1 , r = ^x² +y ²;      (8)

V r r J

R = p m ■ 5 x,- V p p

2 z .

Подставим, например, R из (7) в (2) и преобразуем, получим ф = Р ■ m ■ ln z +

P ln 5 f x,y | + Q V z z J

=P ^*ln z+Q ^*. (10)

Квадратная скобка, очевидно, — однородная функция n кратности как P,Q . Следовательно, форма (10) принадлежит тому же классу (2). Аналогичным образом, встраивая (8) и (9) в (2), можно получить родственные формулы. Опуская значок "*", запишем эти редуцированные к некому каноническому типу выражения для потенциалов (2), ничего не теряя в общности:

ф = Р (x,y,z) lnz + Q (x,y,z),(11)

ф = Р (x,y,z) ln r + Q (x,y,z),(12)

ф = Р (x,y,z) lnp + Q (x,y,z).(13)

Математически в общем смысле все эти формы эквивалентны и лежат в классе (2), но конструктивно они разные, и каждая порождает свой подкласс спектрографических сред. Выбранный способ редукции, отнюдь, не единственный, и можно брать другие варианты функции R , кроме (7), (8), (9), но на данном этапе мы пока никаких явных преимуществ не усматриваем и потому ограничимся формулами (11), (12), (13). Поскольку типы функции R вполне конкретизировались, то на нашем усмотрении остались функции P,Q в уравнении (6). Одну из них мы вправе задать по своему усмотрению, тогда другая должна определяться из (6) как решение соответствующего уравнения Пуассона. Желание построить простой и эффективный метод синтеза искомых потенциалов приводит нас к очевидной мысли, что функцию P ( x,y,z ) выгодно брать в классе гармонических функций

А Р = 0,                (14)

и тогда для Q ( x,y,z ) образуется уравнение типа Пуассона

A Q = - ( 2 V Р ■V ln R + P ■A ln R ) ,    (15)

где в ка честве R сле дует брать одну из функций: z ; r = x ² + y ² ; ρ = x ² + y ² + z ² . Общее решение

(15) должно состоять из частного решения неоднородного уравнения Пуассона и произвольной гармонической функции. Член Q ( x,y,z ) , особенно его негармоническую часть, удовлетворяющую неоднородному уравнению (15), для краткости и выразительности уместно назвать компенсатором, ибо он дополняет комбинацию P ln R , уже нами выбранную (назначенную) до гармонической функции. Определение компенсатора Q ( x,y,z ) с точностью до произвольной аддитивной добавки в виде гармонической функции T ( x,y,z ) является большим благом для формирования спектрографических сред с нужными электроннооптическими свойствами

Q = Q o ( x,y,z ) + T ( x,y,z ) , A T ( x,y,z ) = 0.    (16)

Как в нашей статье [8] и здесь нам удобно взять в качестве стартового элемента P в виде комплексного потенциала Донкина [9]

P = f (to), x + iy

ω=u+ i v=     ,          (17)

z+ρ

ρ= x2 +y2 +z2, где f (to) — произвольная аналитическая функция комплексного аргумента ω . Формула (17) выражает все без исключения однородные потенциалы нулевой кратности, удовлетворяющие трехмерному уравнению Лапласа при любом выборе функции f (to). Для начала возьмем вариант структуры (13) как наиболее простой для анализа и построим потенциал вида

Ф = f ( to ) ln p + Q ( x,y,z ) ,          (18)

найдем компенсатор Q с помощью уравнения (15):

A Q = - ( 2 V f ( to ) -V ln p + f ( to ) -A ln p ) .    (19)

Правая часть здесь комплекснозначна, а следовательно, компенсатор Q также должен быть комплекснозначным, как и весь потенциал φ (18) в целом. Функция f (to) распадается на две гармонические функции, однородные нулевой кратности f (to) = f (x,y,z) + if> (x,y,z).          (20)

Поверхности постоянного уровня здесь f ₁ = const , f ₂ = const суть конусы с общей вершиной в начале координат, и, очевидно, они всегда

ортогональны сферам, но тогда ортогональны и их градиенты, так что

, _x       V fto -V p

V f ( to ) - V ln p = ^J ' ' = 0.

Простое вычисление A ln p дает выражение

A ln p = — ρ ²

В результате уравнение для компенсатора Q (19) примет вид

d ² Q + d ² Q + d ² Q = - f ( to ) d x ²    d y ²    d z ²       p²

Чтобы найти в явной форме какое-нибудь частное решение неоднородного уравнения (23), нам придется ввести особые координаты, связанные с формулой (17). Для отличия от других систем координат их целесообразно назвать координатами Донкина, хотя они в электронной оптике нигде, кроме наших работ, не встречаются, а в классических книгах по математической физике мы находим в кратком изложении вариант сфероконических координат, образованных системой взаимно ортогональных конических поверхностей эллиптического сечения и сфер [10, 11]. При этом указывается в монографии [12], что в теоретической физике они применяются крайне редко. Что касается формулы (17) как источника общих сфероконических координат, то мы нашли только беглое упоминание в известном справочнике по теоретической физике Э. Маделунга [13], но, к сожалению, без малейшего раскрытия этой благодатной темы.

Между тем этот вопрос оказался столь интересным и полезным для нашей общей теории спектрографов, что мы просто обязаны изложить его в достаточной мере подробно. Итак, вернемся к формулам (17) и (20). В зависимости от выбора функции f ( to ) поверхности f 1 = const , f , = const образуют систему взаимно ортогональных конусов самого разнообразного сечения. Функцию f можно подобрать так, что и классические сферические координаты и частный вариант сфероконических координат из [12] войдут в этот класс. Систему конусов дополняем сферами ρ = const . Простейший и в то же время наиболее прозрачный и эффективный вариант:

f = ω = u + i v,

u=

x z+ρ

v=

y _. z + ρ

К этим выражениям добавим третью координату

λ = ¹                     (25)

ρ

Система (32) вполне легко, но несколько длинно разрешается относительно x, y,z . Опуская эти выкладки, сразу же запишем результат:

вместо простых сфер; λ — потенциал кулоновского центра и, следовательно, это гармоническая функция.

Вычислим лапласиан произвольной функции Ф(x,y,z), выражая его в координатах u,v,X. Име ем:

2 u

7 ^- 1 + u² + v² ’

2 v

7 ■ 1 + u ² + v² ’

1 1 - u ² - v²

X ■ 1 + u² +v²"

V Ф - u V u + Ф_v V v + Ф_Х V X ,                  (26)

А Ф = V ( V Ф ) = Ф_ии ( V u ) 2 + Ф . ( V v ) 2 + Ф » ( V X ) 2 +

+ 2 Ф_х V u -V Х + 2 Ф_vX V v -V X + 2 Ф_uv V u -V v +   (27)

+ Ф „ А u + Ф > + Ф , А Х .

uvλ

С помощью выражений (32), (33) преобразуем коэффициенты в (31) и после простых вычислений запишем окончательно

А Ф = Х ² <

Функции u,v,λ гармонические, и кроме того их градиенты взаимно ортогональны, поэтому

( 1 + u ² +v ² ) ² ,

A----- Цф

4           uu

+ Ф_т ) + X 2 Ф хх > .

V v -V Х = V u -V v = V u -V v = 0, А u = А v = А Х = 0.

Кроме вещественных координат Донкина u , v имеет смысл ввести еще комплексные координаты Донкина

Вследствие этого выражение (27) принимает наиболее простой вид:

А Ф = - ( V u ) 2 + Ф ( V v ) ² + Ф хх ( V X ) ².   (29)

Вычисляя градиенты функций u,v, λ с помощью выражений (24), (25), получим

x + iy ω=u+iv=    , z+ ρ x - iy

G T = "  - i v = -----.

z+ρ

Производные по ω,ϖ выразим с помощью,

т. н. операторов Г.К. Колосова [14]

I^V " 1²=I^V v² =

⁽ z ⁺ р )

। '² = Р

Выражение (29) запишется теперь так:

д	= 1 (	д	д
д го	2 ^	ч д u	1 д v^
д	1	f д_	д
	=		+ i
д ет	2 1	,д "	д v

^{А Ф}= ,  ¹ 2 ( ^Ф uu ^+Ф vv ) ⁺ 4 ^Ф ХХ .     (31)

( z + P )               Р

Тогда двумерный оператор Лапласа выразится

формулой

Остается выразить коэффициенты через новые координаты u,v, λ . Для этого запишем систему:

a ² ф а² ф  _A а² ф

₂ +   ₂ = 4        .

a u ²    a v ²     а ю д ш

x

= u, z + x2 + y2 + z2

В переменных ω,ϖ, λ лапласиан (34) примет вид, особенно удобный для наших исследований:

^y = v , x ² +y ² +z ²

, f/ а ф , а ф 1

А Ф = Х ² ( 1 + toG ) 2 —---- + X ^{2 д}-^- .    (38)

|^{v 7} д ю дш      д X ² I

x ² + y ² + z ²

= λ.

Теперь настал момент вернуться к уравнению компенсатора (23). Подставляя А из (38) и выра- жая справа в (23) 2 = λ2 , мы получим равенство ρ2

X ² < ( 1 + гоот ) ²

- Q- + X 2 ^Q | - - X 2 f ( _m ) .   (39)

а _ю б ет      a x ² I ^{v !}

Общий множитель λ ² сокращается, и для Q остается комплексное уравнение Пуассона с произвольной аналитической функцией f ( го ) справа

на) [15]:

"Если в любом гармоническом потенциале Ф ( x,y,z ) преобразовать переменные по формулам

X

( 1 + гоет ) ² -jQ- + X ² \ Q - - f ( го ) .      (40)

д го б ет      б X

x X2+Y2+Z2, =Z z  X2+Y2+Z2

Y X ² +Y ² +Z ^{2 ,}

Поскольку справа в (40) координаты λ нет, то резонно предположить, что искомое частное решение Q также не должно зависеть от λ , тогда следует положить

и домножить его на множитель              , то

X ² +Y ² +Z ²

получится новый гармонический потенциал

Ф ( X,Y,Z ) в переменных X,Y,Z вида

Q-Q ( го, ет ) .

Ф- ,       ---х

X ² +Y ² +Z ²

Для Q ( го,ет ) образовалось легко интегрируемое уравнение

х Ф

X

Y

Z

X ² +Y ² +Z ^{2 ,}X ² +Y ² +Z ^{2 ,}X ² +Y ² +Z ²

( 1 + гоет ) ² -^ Q- - -f ( го ) . (42) ⁽ ) а го б ет ⁽ )

Интегрируя его сначала по ϖ , потом по ω , после простых преобразований получим формулу для Q (го,ет) общего вида t f (го) d го      , .      , .

^{Q- и} 1 '. — ⁺ Р ( ^го ) ⁺ g ( ^и ) ,    ⁽⁴³⁾

1+ ωϖ где p (го) и g (ет) — произвольные аналитические функции комплексных аргументов ω,ϖ , т. е., по сути, свободные донкинские потенциалы. В дальнейшем они будут играть важную роль при решении задачи Коши для симметричных полей, а на данном этапе их можно опустить. Негармонический интегральный член в (43) — также однородный нулевой кратности, является главной частью компенсатора Q . В итоге мы можем записать формулу потенциала нулевой кратности из класса (13)

Ф о ^-f ( ^го ) ln P ^- ^ J ^{f ( го} ) d ^го .          ⁽⁴⁴⁾

1 +ωϖ

Он является порождающим элементом для множества потенциалов класса (13) с целочисленными кратностями n-± 1, ± 2, ± 3,-           (45)

ГЕНЕРАЦИЯ НОВЫХ РЕШЕНИЙ

Мы будем часто пользоваться следующей замечательной теоремой У. Томсона (лорда Кельви-

В геометрическом смысле преобразование координат (46) отвечает инверсии в единичном шаре, "выворачивающем" пространство x,y,z наизнанку, поскольку внешность единичного шара, включая бесконечно удаленную точку, переходит внутрь шара, а его внутренность, напротив, переходит во внешность шара, причем центр уходит на бесконечность. Инверсия (46) не меняет отношений x=X y=Y z Z, z Z.

Поскольку все однородные функции нулевой кратности зависят только от отношений координат, то они также сохраняют свою аналитическую форму. Поэтому нет необходимости в дальнейшем менять обозначения x,y,z на X,Y,Z , дос таточно только изменить ρ = x ² + y ² + z ² на 11

= . Сказанного достаточно, чтобы ρ X ² +Y ² +Z ²

из основной функции φ0 (44) при помощи преобразования Кельвина построить новый гармонический потенциал кратности (-1) вида f (го) d го

1 +ωϖ

Ф - 1 ^- -" 1 f ( ^го ) ln P ^{+ и} J

.

Как вполне очевидно, частные производные от произвольной гармонической функции Ф(x,y,z) любого порядка по x, y, z сами являются гармоническими функциями. Таким способом из потен- циалов (44) и (49) можно образовать великое множество новых гармонических потенциалов. К сожалению, этот процесс уже через несколько шагов начинает так ветвиться, что мир этих функций становится практически необозримым и ценность их для теории спектрографов становится неуловимой. На самом деле нам нужны достаточно простые и математически прозрачные структуры. Их мы сможем получить, пользуясь только операто ром . Запишем (49) в более удобной форме az

- f ( to ) ln p + Q ( to,m ) P

С помощью выражений легко найти следующие величины, которые будут постоянно возникать в наших аналитических конструкциях:

d to = - to d m = -m z = 1 - torn d z p ’ d z p ’ p 1 + tom

Дифференцируя (50) по z, с учетом формул (51) получим потенциал ф-2 кратности (-2) по фор- щиеся новые структуры с учетом всех упрощений, которые будут возникать по ходу дела.

РЕКОНСТРУКЦИЯ ПОТЕНЦИАЛЬНЫХ СТРУКТУР КЛАССА (2)

Теперь рассмотрим несколько конкретных примеров потенциальных структур данного класса трехмерных потенциалов (2). Если P и R определены, то необходимо найти функцию-компенсатор Q

,      .        с f ( to ) d to

Q ( to,m ) = - m(     —.        (54)

1 + tom

Несмотря на кажущуюся простоту, этот интеграл берется в элементарных функциях только для f (to) в виде конечных полиномов, либо отношения полиномов; иных вариантов, по-видимому, нет. Ограничимся только целыми степенями f = ton,n = 1,2,3,-.           (55)

Из таких элементов складываются полиномы, и класс интегрируемых вариантов f ( to ) становится достаточно богатым.

муле ф-2

Р ^

tof ( to ) + f ( to )

1 - mto

1 + tom

ln p -

Пример 1. f = to .

P'

1 -mto    1 -mto f (to)T7— + QTZ— + Q™to + Q™m . (52)

1 + tom    1 + tom

„     с tom d to          1 . /. х

Q = - ------ = - to + —ln ( 1 + tom ) .       (56)

^J 1 + tom       m

Благодаря комплексным донкинским переменным to, m аналитические структуры довольно компактны. Но уже при разбиении полученных структур на вещественную и мнимую части количество новых гармонических структур удваивается, и, вот, они будут действительно очень громоздкими. Для генерации новых структур, помимо дифференцирования по координате, мы можем применять и преобразование Кельвина (47); из (52) образуем очень интересный физически содержательный потенциал кратности (+1) с помощью преобразования Кельвина

Несущественную гармоническую составляющую to можно отбросить, и полный потенциал по формуле (44) предстанет в виде

ф 0 =to ln p + —ln ( 1 + tom ) . ϖ

Ф + 1

^- Р

tof ( to ) + f ( to )

1 - mto

1 + tom

ln p -

^- P

^{f ( to} )

1 - mto

1 + tom

1 - mto

+ Q----

1 + tom

■ O.o-Om

Таким образом, мы проиллюстрировали общий аналитический алгоритм создания новых структур, но при конкретном выборе производящей f ( to ) более выгодно делать реальные выкладки, начиная со структуры (44), и далее вычислять получаю-

Пример 2. f = to ² .

„ г to²m d to to to ²     1 ,            x

Q = - --------=-----^ln ( 1 + tom ) .

J 1 + tom m   2   m2 v ’ to2

И здесь, отбрасывая , получим

to ф0 = to lnp + — ϖ

—iyln ( 1 + tom ) . ϖ ²

Пример 3. f = to ³.

^Q= 4

to³m d to

1 + tom

to

to2

---+-- ϖ ² 2 ϖ

- ^to+—- ln ( 1 + tom ) . (60)

3 ϖ ³

Снова игнорируя гармонический член

-^ 1

I , V 3 7

получим потенциал

ф 0 = to ³ln p

—

to to 2       1

— ⁺ z— ⁺ —^{ln (1 + to}® ) .

ϖ 2 ϖ ϖ

С ростом n число членов растет, но не слишком быстро, при этом в структуре выражения потенциала наблюдается некое единообразие. Каждый из этих потенциалов служит зародышем для целой цепочки потенциалов с отрицательными и положительными кратностями. Размножение этих конкретных структур происходит чрезвычайно быстро, и всех их обозреть практически невозможно. Ограничимся самыми лаконичными иллюстрирующими примерами.

Подвергнем преобразованию Кельвина потенциал (57)

ф — 1

— to ln p  11,/,     /

---— + — —ln ( 1 + to® ) p   p V ™

Воспользуемся далее формулой (52) и построим потенциал кратности (–2). Даже в этом простейшем случае последовательность формул неожиданно оказывается весьма нетривиальной. Опуская алгебраические выкладки, запишем окончательный результат

ф _— 2 = —--^to — {2ln p — 3 + torn + 2ln ( 1 + to^ ) } . (63)

p 1 + torn

Это выражение можно снова продифференцировать по z и получить потенциал кратности (-3) и так далее. Преобразованием Кельвина потенциал (63) можно превратить в потенциал кратности (+1):

ф_{+ 1} = p • —^to — {— 2ln p — 3 + tow + 2ln ( 1 У® ) } . (64)

Чтобы понять физическую природу этих потенциалов, перейдем от абстрактных донкинских координат to, ст к обычным декартовым. Пользуясь формулой

,         , x ² + y ²     2р

1 'И® 1 +----—₇ =——,      (65)

( z + p ) ²    z + p ' '

получим

In p — 2 + ^P + ln ^2p | . (66) z+p z+p

— 1 x + i y

Ф — 2 = ~-- p ² p

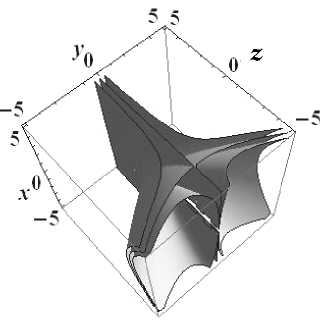
Рис. 1. Эквипотенциальные поверхности структуры

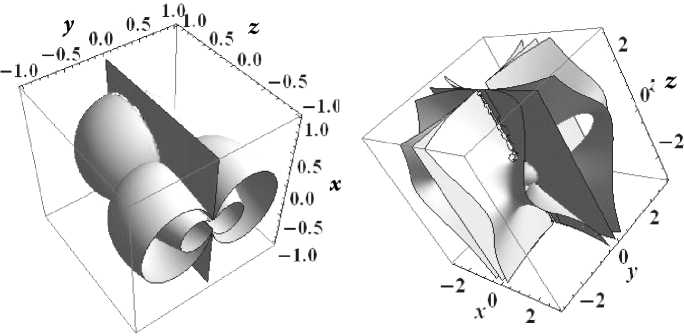
Рис. 2. Эквипотенциальные по- верхности структуры ности структуры

Рис. 3. Эквипотенциальные поверх-

Ф+1 =yln (z + p) + -y^ . z+p ф+1 =C = const = -1, 0, 1

ф_₂= -y |^2ln p ⁺ ^— ^— ln ( z + p )

p ² I z + p ^x ’

Ф _{— 2} = C = const = -5, -2, 0, 2, 5

ф 0 =

2 xy

( x - +y - ) ²

X

^X{ ( ^z+p ) ²ln ( ^z+ p ) — 4 zp In p } +

+ ^2 x 4. x ² +y

ф ₀ =C = const —2, 0, 2

Преобразуем (66) по Кельвину, тогда получится выражение

/      - \ 1. 1 ~ р . 2р

Ф + 1 = ( х + i у К1п— 2 +----+ 1п----

[ р z + р z + р

= ( xi iу )х

I „ o+z-z , - ,     . / х х<-1пр - 2+—------+ 1п2 + 1пр - 1п (z + р)

[            z + р

= ( х + iу )<( 1п2-1)

z z+ρ

- 1п ( z + р )

Отбрасывая тривиальный двумерный гармонический член ( х + i у )( 1п2 - 1 ) и меняя знак, мы напишем, отнюдь, нетривиальный обобщеннооднородный гармонический потенциал с кратностью (+1) вида

φ + 1 =

( х + i у ) 1п ( z + р ) +

z ( х + i у ) z+ρ

На рис. 1–3 представлены эквипотенциальные поверхности потенциальных структур изучаемого класса с разной кратностью.

ВЫВОДЫ

Подведем итоги. С помощью комплексных потенциалов Донкина мы можем строить огромное многообразие обобщенно-однородных гармонических потенциалов с целочисленными кратностями и затем изучать их с той или иной степенью подробности либо чисто аналитическими способами, либо компьютерным моделированием, но лучше комбинацией того и другого. Меняя f ( го ) только в классе полиномов и отношения полиномов, мы образуем очень пестрый и богатый мир спектрографических сред с неограниченными возможностями.

• 3.    Габдуллин П.Г., Голиков Ю.К., Краснова Н.К., Давыдов С.Н. Применение формулы Донкина в теории энергоанализаторов. I // ЖТФ. 2000. Т. 70, № 2. С. 91–94.

• 4.    Габдуллин П.Г., Голиков Ю.К., Краснова Н.К., Давыдов С.Н. Применение формулы Донкина в теории энергоанализаторов. II // ЖТФ. 2000. Т. 70, № 3. С. 44–47.

• 5.    Левин В.И., Гросберг Ю.И. Дифференциальные уравнения математической физики. М., Л.: Гос. изд-во физ.-мат. лит-ры, 1951. 576 с.

• 6.    Read F.H. The parallel cylindrical mirror electron energy analyzer // Rev. Sci. Instrum. 2002. V. 73, N 3. P. 1129–1139.

• 7.    Голиков Ю.К., Григорьев Д.В., Соловьев К.В., Уткин К.Г. Новый базисный ряд осесимметричных гармонических потенциалов для синтеза энергоанализаторов // Тез. докл. 4 Всерос. сем. "Проблемы теоретической и прикладной электронной и ионной оптики". Москва, 1999. C. 11–12.

• 8.    Голиков Ю.К., Краснова Н.К. Электрические поля, однородные по Л. Эйлеру, для электронной спектрографии // ЖТФ. 2011. Т. 81, № 2. С. 9–15.

• 9.    Уиттекер Э., Ватсон Дж.Н. Курс современного анализа. В 2 т. Т. 2. М.: Физматгиз, 1963. 516 с.

• 10.    Морс Ф.М., Фешбах Г. Методы теоретической физики. В 2 т. Т. 1. М.: Изд-во иностр. лит-ры, 1958. 930 с.

• 11.    Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, гл. ред. физ.-мат. лит-ры, 1968. 720 с.

• 12.    Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970. 712 с.

• 13.    Маделунг Э. Математический аппарат физики. М.: Изд-во физ.-мат. лит-ры, 1960. 618 с.

• 14.    Голиков Ю.К., Краснова Н.К. Теория синтеза электростатических энергоанализаторов. СПб.: Изд-во Политехн. ун-та, 2010. 409 с.

• 15.    Томсон У., Тэт П. Трактат по натуральной философии. Ч. II. М., Ижевск: НИЦ "Регулярная и хаотическая динамика", Ижевский институт компьютерных исследований, 2010. 592 с.

Санкт-Петербургский государственный политехнический университет