Аналитический метод построения области возможного изменения текстурных параметров

PNRPU MECHANICS BULLETIN

Одним из традиционных направлений науки о металлах является создание материалов с заданным комплексом служебных характеристик, т.е. таких сплавов, которые обеспечивают необходимый уровень тех или иных технологических или эксплуатационных свойств – пластичности, прочности, вязкости, долговечности. Помимо классических методов управления свойствами за счет изменения состава и структуры сплава, в некоторых случаях создание требуемых характеристик осуществляется за счет наведенной анизотропии, которая обусловлена кристаллографической текстурой и возникает вследствие той или иной термомеханической обработки. Широко известны, в частности, примеры создания оптимальной текстуры в листах малоуглеродистой стали для повышения их штам-пуемости в автомобильном производстве и оптимальной текстуры холоднокатаного кремнистого железа для уменьшения потерь энергии при перемагничивании в производстве трансформаторов. Применение математических моделей высокого уровня [1], связывающих внутренние параметры материала с возникающей в процессе глубокой пластической деформации текстурой, позволяет научно обоснованно управлять анизотропией физико-механических свойств [2–10].

Как показано в исследованиях [11, 12], многие физико-механические свойства макроскопически ортотропных текстурированных металлов и сплавов с кубической симметри- ей кристаллической решетки определяются текстурными параметрами, которые имеют вероятностно-геометрический смысл и определяются равенствами

A i =( qQ + Q 2 q 2 + a² q 2 ), a— i, 2,3),                    (i)

где Q_ij – элементы матрицы поворота, определяющей положение кристаллографических осей случайным образом ориентированных зерен поликристалла в лабораторной системе координат, связанной с ототропным образцом; (.. - операция осреднения по представительному объему текстурированного поликристалла.

Текстурные параметры (1) под названием «ориентационные факторы» впервые были введены в работе [13] для установления количественной связи кристаллографической текстуры с упругими свойствами металлических материалов, имеющих объемно-центрированную и гранецентрированную симметрию кристаллической решетки. В дальнейшем этим параметрам давались и другие названия – инварианты анизотропии, интегральные характеристики текстуры, параметры деформационной анизотропии, отражающие их математическую и физическую сущность [14,15].

В частности, связь средних значений коэффициентов податливости с текстурными параметрами в приближении Ройса, когда поле напряжений в поликристалле считается однородным, т.е. не изменяется при переходе от зерна к зерну, устанавливается равенствами sRi — sn -2sAi,

^s 22 = s ii   ^{2 s A} 2 ,

^R s ₃₃

= sn -2sA3,

^S i2 = ^S i2 ^{+ S} ( ^A i ^+A 2   ^A 3 ) ,   ^S 23 = ^S i2 ^{+ S (A} 2 ^{+ A} 3   ^A i ) ,   ^S i3 = ^S i2 ^{+ S} ( ^A i ^{+ A} 3   ^A 2 ) ,

sR4 = S44 + 4S (A2 +A3 -Ai ) , S5R = S44 + 4S (Ai + A3 —A2 ) , S66 = S44 + 4S (Ai +A2 — A3 ) •

Здесь s = s _ii - s _i2 - 0,5 s ₄₄, s _ii, s _i2, s ₄₄ - коэффициенты податливости монокристалла.

Другой предельный случай расчета упругих свойств реализуется в схеме Фойгта, когда предполагается, что кристаллиты одинаково деформируются. В этом случае связь средних значений модулей упругости с текстурными параметрами определяется соотношениями cVi — cn -2cAi,

^V c 22

— Cii — 2 c A 2 ,   C 33

= С и - ² c A 3,

ci2 = ci2 + c (Ai +A2  A3 ),  c23 = ci2 + c (A2 + A3  Ai ) ,  ci3 = ci2 + c (Ai + A3  A2 ), c44 = c44 + c (A2 +A3 Ai ), C5 5 = c44 + c (Ai + A3 A2 ), c66 = c44 + c (Ai +A2 A3 ) •

Здесь c — c _ii - c _i2 - 2 c ₄₄, c _ii, c _i2, c ₄₄ - модули упругости монокристалла.

Как показано в монографии [11], в случае трансверсальной изотропии текстурированного поликристалла между текстурными параметрами существует связь:

^A i,2 =

50 + З А 3 ) 8

Здесь индекс 3 относится к оси трансверсальной изотропии анизотропного материала.

Если поликристалл квазиизотропен, то

А1 = Д 2 = Д3 = 0,2.

Зависимость модуля Юнга от направления в плоскости Ox ₁ x ₂ лабораторной системы координат имеет следующий вид:

E - 1 (_ф) = 5 11 - 0,25 5 [ 1 + 3 Д 3 + 4 ( А 1 -Д ₂ ) cos 2 ф + ( 4 Д 1 + 4 А ₂ - 3 А ₃ - 1 ) cos 4 ф] .

Угловая зависимость коэффициента Пуассона в плоскости Ox1x2 ортотропного тек- стурированного материала определяется равенством

5 [ 1 - Д ₃ + ( 4 Д 1 + 4 Д 2 - 3 Д ₃ - 1 ) cos4 9^ + 4 5 12

(Ф) = 5[1 + 3Д3 + 4(Д1 -Д2)cos2ф + (4Д1 + 4Д2 -3Д3 -1)cos4ф] -451/

• 1.    Построение области возможного изменения текстурных параметров

В общем случае возможная анизотропия ортотропного текстурированного поликристалла с кубической симметрией структуры определяется положением точки в замкнутой области распределения текстурных параметров. Эта область может быть построена аналитически, исходя из следующих ограничений [16]:

Д1 + Д2 + А3 - 2А12 + А2 + Д2 - Д1Д2 - Д2Д3 - Д3 Д1 < 1,

0 < А 1 +А ₂ -Д ₃, 0 <А ₂ +Д ₃ -А 1 , 0 <Д ₃ +Д 1 -А ₂.

Эти равенства вытекают из условия положительности весовых коэффициентов в соответствующей задаче усреднения – определении средних степенных взвешенных собственных значений оператора упругости текстурированного поликристалла [17,18].

Инвариантность этих неравенств к циклической перестановке индексов означает, что искомая область, построенная в декартовой системе координат O Д 1 Д ₂ А ₃, имеет ось симметрии третьего порядка, одинаково наклоненную к декартовым осям.

Переходя в первом уравнении системы (2) к равенству

Д1 + Д2 + Д3 - 2Д12 + Д2 + Д2 - Д1Д2 - Д2 Д3 - Д3 Д1 = 1

и выполняя тождественные преобразования, находим

• 3 (д 2 + Д 2 + А32)- 6 (Д 1 Д2 + Д 2 А3 + Д3 А1) + 2 (Д 1 + Д2 + Д3)-1 = 0.            (3)

Уравнение (3) задает коническую поверхность, и искомая область находится путем построения линий пересечения этой поверхности с плоскостями, определяемыми тремя последними неравенствами системы (2). Дальнейшее построение всех элементов кусочногладкой поверхности, ограничивающей область изменения текстурных параметров, может быть выполнено путем перехода к цилиндрическим координатам с использованием векторно-матричного алгоритма.

На первом этапе, полагая в уравнении (3) Д 1 = Д ₂ = Д ₃, определяются координаты вершины конуса

^Д 1 = ^Д 2 = ^Д з = з

.

Далее, находятся координаты пересечения конической поверхности с осью O Д 1 : 2

Д1 = з, и угол а при вершине конической поверхности, а = arcsin

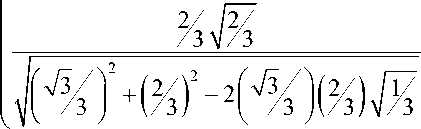
Уравнение конической поверхности в цилиндрической системе координат может быть представлено в следующей векторно-матричной форме:

Г (s, ф) = "s + l (ф)р(s),

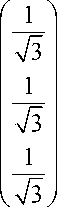
единичный вектор, определяющий положение оси конуса;

/ (ф) = A

' V2/s' -1/V6 <-W6,

- азимутальный вектор при произвольном значении полярного угла ф ,

ортогональный вектору "  ; A - матрица поворота на угол ф вокруг вектора n ,

	Г cos ф	n - т-7 Sin ф I " 1	"у ■ Sin ф 1 " 1
A =	n т-7 Sin ф " 1	cos ф	n - т Л Sin ф 1 " 1
	ny - T^Sin ф I I n i	n ’ Sin ф 1 " 1	COS ф 7

Р( s ) = [l/( Уз )2 +(Уз )2 +(Уз 1 - s ]

tan а - полярный радиус.

После выполнения тождественных преобразований находится вид азимутального вектора l (ф),

3cos ф

^{1 (}ф ) =

1         . V2 .

——cos ф +--Sin ф

V62

1         V2.

—P cos фsin l Vs а с учетом равенства (4) находится функция р( 5):

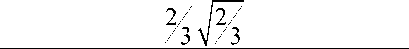
I I ^/2 2|        2/1 П7

I7э I ш /з J +(/з) 21 /з R/зН/з c5 , c =      ’—

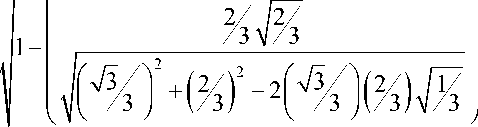
В итоге уравнение конической поверхности, ограничивающей область изменения текстурных параметров, может быть представлено в следующем виде:

^1 I

A 2 v^A 3 j

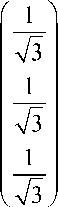
I 2 I j 3 co s ф
1         V2 . --;=cos ф+--sin ф V6      2	7з p ( 5 ) . 0 < 5 < —
1         V2 . --т= cos ф-- sin ф l V6       2 J

0 < ф < 2n.

Для определения линии пересечения плоскости A ₂ + A ₃ - A 1 = 0 и конической поверхности выполняется переход к цилиндрическим координатам в уравнении этой плоскости с помощью соотношения (5):

s

——cos фр ( 5 ) = 0.

Отсюда

4 c

5 (ф) =

—;= cos ф 6

4 c

1 + —;= cos ф

Путем подстановки этой функции в уравнение конуса (5) находится уравнение линии пересечения плоскости с конической поверхностью

r ( ф ) =

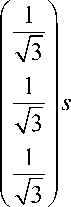
(ф)+

f 2

J 3cos ф

1          . 72 .

--— cos ф +-- sin ф

V62

1         V2.

—^cos ф к 762

( 1                к

- 5 (Ф)к V 3       J

Тогда уравнение первой грани области распределения текстурных параметров имеет вид

r (v, ф) = v

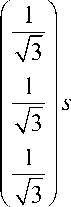
(ф)+

^3cos Ф

——cos ф+ --sin ф

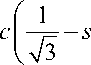
( ф )

J

7t 7t

, 0 < v < 1, <ф<-.

—;=cos ф--sin ф

2-

Две оставшиеся грани находятся преобразованием поворота первой грани на угол 3

и ^— вокруг оси симметрии с помощью уравнений

r2 (v, ф) = ri (v, ф) +

^f L

к

-

2 -к _ . 2 - cos— + L sin —

3 J 3

к

J

r ₁

( v , ф ) , 0 <  v <  1,

-

-     -

— <ф<—, 33

^r 3 ( ^v , ф ) = ^r 1 ( ^v , ф ) ⁺

L2|1 к к

4-к т . 4-) - cos— + L sin —

3 J 3 J

^A r ₁

( v , ф ) , 0 <  v <  1,

-

-

-

— <ф<—, 33

где

		1	1 к
	0
		3	3
	1		- 1
L =		0
	73		3
	1	1
			0
	к 73	3	J

Участки конической поверхности, ограничивающей область распределения текстурных параметров, определяются уравнениями

4 (v, ф) = (1 - v) r (ф) + v

0 < v < 1,

П

П

— <ф<—, 33

Г2к ( v, ф) =

A / x , f             2n) , T • 2n)

r _1k ( v , ф ) + 1 L I 1 - cos — 1 + L s^m~

П

П

--<ф<—, 33

r3k (v, ф) =

I          4n I          4n

• r ik ( v , ф ) + L I 1 - cos— l + L sin —

I V        3 7        3 7

n

n

• - < ф <

• 2.    Траектория текстурных состояний при непрерывной горячей прокатке алюминиевых сплавов

Два элемента поверхности, ограничивающие область изменения текстурных параметров, заданных уравнениями / 11 = / 11 ( v , ф ) и r_lk = r_lk ( v , ф ) , изображены на рис. 1.

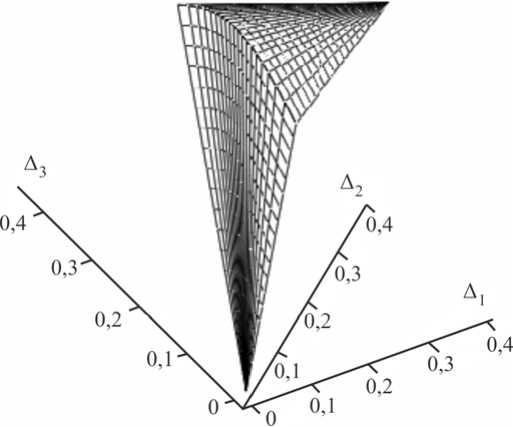
Рис. 1. Формообразующие элементы поверхности, ограничивающей область изменения текстурных параметров

Как известно, различные режимы термомеханической обработки приводят к изменению текстуры металлического материала, что сопровождается изменением соответствующих текстурных параметров. Это изменение позволяет в общем случае построить траекторию текстурных состояний, которая не будет выходить за границы найденной области. При этом каждой точке траектории соответствует определенная анизотропия как упругих, так и пластических свойств. В работе [19] в рамках решения задачи получения в металле эффективной пластической анизотропии было выполнено исследование трансформации кристаллографической текстуры в процессе непрерывной горячей прокатки алюминиевых сплавов в 5-клетевом стане «2800», и выполнен расчет соответствующих текстурных параметров (таблица).

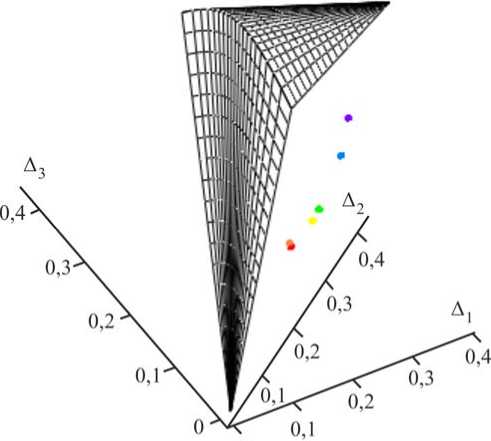
Эволюция текстурных состояний при прокатке алюминиевого сплава в 5-клетевом стане непрерывной прокатки представлена изменением положений соответствующих точек в найденной области возможных значений текстурных параметров (рис. 2).

Изменение параметров текстуры Δ _i на выходе из клетей непрерывной группы стана «2800»

о

Номер клети	Толщина подката, мм	Текстурные параметры Δ i
		Δ 1	Δ 2	Δ 3
Исходный раскат	52	0,13	0,118	0,147
1	27,7	0,136	0,12	0,147
2	14,07	0,147	0,158	0,164
3	7,97	0,15	0,16	0,184
4	5,09	0,186	0,192	0,242
5	3,0	0,216	0,205	0,282

Рис. 2. Траектория текстурных состояний на выходе из клетей непрерывной группы стана «2800», • – исходный раскат, • – 1 клеть, • – 2 клеть, • – 3 клеть, • – 4 клеть, • – 5 клеть

Заключение

Для текстурированных поликристаллических материалов с кубической симметрией структуры найдены в аналитической форме границы области изменения текстурных параметров, являющихся интегральными характеристиками текстуры и определяемых с помощью косвенных или прямых методов текстурного анализа. Показано, что эволюция текстуры на различных стадиях термомеханической обработки металлических материалов может быть геометрически представлена траекторией текстурных состояний. При этом каждой точке траектории соответствует уникальное анизотропное состояние, которое может быть охарактеризовано известными соотношениями между константами анизотропии соответствующих физико-механических свойств и текстурными параметрами. Предложенный подход может быть использован при решении задач целенаправленного достижения комплекса требуемых технологических или конструкционных свойств полуфабрикатов и изделий из металлических материалов с ОЦК и ГЦК-структурами [20]. Достаточно перспективна возможность установления связи рассмотренных в данной работе текстурных параметров с коэффициентами функции распределения ориентации (ФРО), широко используемой в современных методах количественного текстурного анализа. В рамках этого подхода возможно решение принципиально новой важной в теоретическом и практическом плане задачи – построение границ области возможного изменения трех значимых коэффициентов разложения ФРО.