Аналитический метод расчета регулятора для колебательной системы с двумя степенями свободы

Целью работы является разработка метода синтеза оптимального регулятора для колебательной системы с двумя степенями свободы, описывающей малые колебания относительно ее программного движения или состояния покоя. Для решения данной задачи используются принцип динамического программирования Беллмана и теория аналитического конструирования оптимальных регуляторов (АКОР) Летова [1]. Рассматриваемые методы предлагается использовать совместно с методом усреднения [2]. Такой подход позволяет понизить размерность задачи и, тем самым, значительно упростить ее решение.

Рассматриваются колебательные системы, поведение которых описывается следующей системой обыкновенных дифференциальных уравнений

_ d ² x dt ²

( dx )

+ Cx = ЕQ x,— + еmu, (1) V dt)

где x – n -мерный вектор переменных состояния системы, A и C – известные квадратные симметричные матрицы, e - малый параметр

L ^dx )

задачи, Q x,--

V dt)

– вектор-функция возмуще-

управления системой (1) и ⁰ с целью демпфирования колебаний, то есть решается задача о переводе системы в начало координат. Причем оптимальность управления u понимается в смысле минимума квадратичного функционала

J = Е £* (KTaK + cu2 )dt,     (2)

где a - положительно определенная матрица весовых коэффициентов для ошибок управления, n >  0 ^- весовой коэффициент для управления, K - вектор амплитуд колебаний, I T I - знак транспонирования, t k – время перехода.

Применение метода усреднения к системе (1) предполагает замену переменных в этой системе в соответствии с формулами

n

x = Ё KV(1 )cos^ i), i=1

dx = - ^LK_l ю V ^{(1 )sin}to. ^{1         (3)}

dt       i = 1

где ф - вектор фаз колебаний.

Применяя стандартную процедуру перехода к переменным “амплитуды – фазы”, получим дифференциальные уравнения для новых переменных ний, действующих на систему; m – матрица, определяющая структуру управляющего устройства в конкретной задаче; u – скалярное управление.

Предполагается, что для системы (1) выполнены условия управляемости и наблюдаемости [3].

Решается задача определения оптимального

dK = Е X(K, ф)+ Е Y(ф) и, dt

^ = Ш + еФ(K,ф)+ЕТ(K,ф)и, (5) dt где вид функций известен.

Согласно принципу динамического программирования Беллмана, сформулированному для непрерывных динамических систем, оптимальное управление определяется из условия [1]

min

u

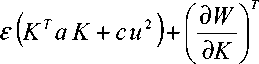
dK

— + dt

( K 0 ) ^T aK ⁰ +I W ■( X ( K 0, ф‘

f д W 1 T d^ к Эф7 "dt

= 0,

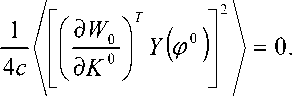
где w ( K , ф ) – производящая функция.

Подставляя систему (4), (5) в условие (6) и собирая вместе слагаемые, зависящие от управления, получим функцию

H( u) = ecu2 +

+ e u

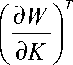
T

Y^{(ф ) +} Iko к ^дф 7

^ ( K , ф )

. (7)

д НИз условия минимума этой функции "Г = 0 нетрудно определить оптимальное управление где оператор ... есть стандартный оператор усреднения.

Уравнение (10) существенно проще исходного уравнения (9), так как слагаемые в него входящие зависят только от амплитуд и не зависят от фаз, причем, то же самое справедливо и для производящей функции W ^ ( K 0

Для обеспечения динамической устойчивости точки равновесия колебательной системы

dx

X =--= 0 функция dt

W ₀ ( K ⁰ ) , удовлетворяю-

T

u

2 c

T

+[ Z) -к •*)

.

Оптимальное управление u ⁰ найдено с точностью до производящей функции W ( K , ф ) . Для определения дифференциального уравнения для этой функции необходимо подставить выражение (8) в условие (6), тогда

щая уравнению (10), должна быть положительно определенной. В этом случае функцию W 0 ( K ⁰ ) можно рассматривать как функцию Ляпунова, обеспечивающую устойчивость решения K ⁰ = 0 для усредненной системы [4].

Здесь надо отметить, что с учетом соотношений (8) и (10) оптимальное управление в первом приближении можно записать в виде

u0

12c

eKTaK + e

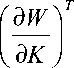
f d W 1 T

к дк0 7

Y ( ф 0 )

+ £..., (11)

+

( д W ) T к дф 7

e

4 c

X (K, ф)+

\о + еФ( K, ф)]-

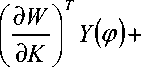
fdWiT т( k , ф)к дф 7

= 0.

то есть слагаемые пропорциональные e можно не учитывать, так как при подстановке (11) в уравнение для амплитуд (4) эти члены изменяют только второе приближение метода усреднения.

Рассмотрим колебательную систему в форме (1) с двумя степенями свободы при наличии линейных возмущений, т.е когда n = 2 и

Q=Rdx.dt

Усреднение двухчастотной системы

Для решения уравнения (9) предлагается применить метод усреднения, который заключается в поиске решения в виде асимптотических рядов. Подставляя известные формулы метода усреднения в уравнение (9) и усредняя это уравнение по фазам ф^ ( i = 1,...n) и удерживая слагаемые только порядка £ , получим позволяет представить результаты анализа колебаний в наглядной форме с помощью метода фазовой плоскости в координатах (K 10 , K2 )[5].

Из приближенного уравнения для производящей функции W 0 ( K ⁰ ) следует, что для ее определения в первом приближении достаточно рассмотреть только уравнения амплитуд (4). Эти уравнения для случая n ₌ 2 имеют вид

dK

—1 = -fN4 Q + m u) - N2 (q2 + m 2 u)] • dt                                         (12)

• sin^1.

b ₂₂ - A ₂₂ • ^ 2 • ( N 3 • ^ 11 + N 3 • ^ ₁₂ • X ₂ -

- N1 • А21 - N1 • ^22 • Z2)-

1 2                               2

--A ₂₂ ( N₄ • m_x - N 2 • m ₂) = 0,

2 c

K = f[ N3 (Qi dt

• sin^2.

+ m1 u) - N1 (Q2 + m 2 u)] •

где

N 1 =

^A 11 ⁺ A 12 X 1

to 2 (X 2 -X1 )(A11A22 - An ) ’

N 2 =

A 11 ⁺ A 12 X 2

to- (X2 -X1 )(A11A22 - An ) ’

полученных путем подстановки функции Ляпунова W 0 ( K ⁰ ) в уравнение (10) и приравнивании к нулю коэффициентов при K ₁ ² , K ₂ ² , K 1 K 2 , а коэффициенты Ц-ц, Ц 12 , Ц 21 , Н 22 определяются из вида возмущающей функции Q . Нетрудно показать, что A 12 = 0 . При использовании положительных корней уравнений (15), (16) для A ₁₁ и A ₂₂ будут выполняться условия Сильвестра, что обеспечивает асимптотическую устойчивость усредненной системы.

В итоге усредненная система примет вид

N 3 =

A 12 ⁺ A 22 X 1

to 2 (X 2 -X1 )(A11A22 - An ) ,

dK10 dt

е _л    ^0 ^{( N} 4 • ^m 1 ^{- N} 2 • ^m 2 ⁾²

о A11 ^ K12c

N 4 =

_______ A 12 ⁺ A 22 ^X 2 _______

to1 (X 2 -X1 )(A11A22 - An ) '

dK20 dt

е

-

2

Учитывая, что

Здесь матрица собственных векторов невоз-

мущенной системы представлена в виде

V =

f1

к X1

¹ ]

V

X 2 /

, где ^X 1,2

– коэффициенты форм

колебаний. Полное преобразование к переменным “амплитуды – фазы” для двухчастотной системы вида (1) приводится в [5].

После перехода к переменным “амплитуды-фазы”, формула для определения управления примет вид

U 0 = -A _n • K 10 ( N ₄ • m 1 - N ₂ • m ₂)sin( ^ ₁) - c

1        ₀                                     (14)

— A ₂₂ • K ₂ ( N ₃ • m 1 - N 1 • m ₂) sin( ^ ₂),

c

где коэффициенты A ₁₁ и A ₂₂ будут положительными корнями уравнений

b11 - A11 • to1 • (-N 4 • ^11 - N 4 • Д12 • %1 +

^{+ N} 2 • Д 21 ^{+ N} 2 • ^ 22 • % 1 ) ^-

1 2                              2

- —A n ( N 4 • m 1 - N 2 • m 2 ) = 0, 2 c

(N3 • m1

- N1 • m2 )2

c

K1 sinto =  / Z2—? xty +^1 (Z2 - %1 )

1

⁺ —.-------г ^x 2 ,

^1 (Z2 - %1 )

K2 Sin(^2) = ---T^1----X -x1 -

Ю2 (Z2 - Z1 )

1x. ^2 (%2 - %1 )

запишем управление в исходных координатах

U = p 1 x1 + p 2 x 2,

где коэффициенты

P 1 =

•

•

% 2

c ^ 1 ⁽ % 2

% 1

%1 )

A 11 • ( N ₄ • m

N ₂ • m ₂)

c

^to 2 ⁽ % 2

% 1 ⁾

A ₂₂ • ( N ₃ • m ₁

N ₁ • m ₂ )

Р2  ---7--------\ All • (N4 • ml — N2 • m2) +

c ^1U - Z1 )

H—------- ? A 22 • ( N з • m i — N i • m 2 )•

c ®2 (Z2 — Z1)

Таким образом, применение метода усреднения в сочетании с методом динамического программирования Беллмана позволило получить аналитическое решение (18) для оптимального управления системой (1).