Аналитический метод расчёта преломляющих оптических элементов для формирования заданных двумерных распределений интенсивности

В течение нескольких последних десятилетий производительность светодиодов быстро увеличивалась, что способствовало стремительному росту производства и продаж светодиодных систем освещения. Светодиоды превосходят многие традиционные технологии освещения с точки зрения энергоэффективности, срока службы, универсальности и качества цвета, а благодаря демократичной цене успешно конкурируют в различных светотехнических приложениях [1].

Для формирования заданных световых распределений в светодиодных системах освещения используется так называемая вторичная оптика (преломляющие или отражающие оптические элементы, устанавливаемые непосредственно над излучающим элементом светодиода). Расчет преломляющей поверхности из условия формирования заданного распределения интенсивности является обратной задачей неизображающей оптики. Методы решения этой задачи можно условно разделить на две большие группы в зависимости от влияния размеров источника излучения на расчеты.

В случаях, когда размерами источника пренебречь нельзя, как правило, используются оптимизационные методы, требующие больших временных и вычислительных затрат [2– 12]. В данных методах расчет параметров оптического элемента осуществляется из условия минимизации некоторой целевой функции, с помощью которой измеряются оптические характеристики системы освещения. Результат и скорость сходимости процедуры оптимизации сильно зависят от начальных значений параметров, которые обычно задаются с использованием приближения точечного источника излучения.

В случаях, когда влиянием размеров источника излучения можно пренебречь, обратная задача сводится к решению нелинейного дифференциального уравнения в частных производных эллиптического типа (типа уравнения Монже–Ампера) [13– 16]. Аналитические решения данного уравнения получены только для задач, обладающих осевой симметрией, и для ряда задач формирования однопараметрических распределений освещенности [17–23]. «Прямое» численное решение уравнения данного типа методом конечных разностей приводит к решению системы нелинейных уравнений большой размерности (система содержит от нескольких тысяч до нескольких десятков тысяч нелинейных уравнений) [24–26]. Для решения данной системы используются итерационные методы, например, метод Ньютона. В силу сложности задачи решения системы нелинейных уравнений для расчета оптических элементов широко используются т.н. методы лучевого отображения [19–23, 27–39]. Под лучевым отображением понимается функция, представляющая координаты лучей, преломленных или отраженных оптической поверхностью, в зависимости от координат лучей, вышедших из источника излучения.

В ряде «инженерных» методов [30–39] лучевое отображение выбирается эвристически, в виде, который позволяет в относительно простой форме рассчитать параметры отображения из закона сохранения светового потока. Важно отметить, что получаемое отображение должно удовлетворять условию интегрируемости [30], которое определяет возможность построения оптической поверхности, реализующей это отображение. Простые эвристические отображения, как правило, не удовлетворяют условию интегрируемости и позволяют получить только приближенное решение с невысокими рабочими характеристиками [30–33]. Для улучшения таких приближенных решений используются дополнительные методы оптимизации [34, 38]. В частности, в работе [38] полученное на начальном шаге лучевое отображение оптимизируется с использованием метода обратной связи. Такой подход позволил авторам лишь незначительно улучшить световое распределение в требуемой прямоугольной области: равномерность формируемого распределения увеличилась с 50% до 87%. Тем не менее, судя по представленным в работе изображениям (см. рис. 9 в [38]), эффективность полученного решения достаточно низкая, поскольку значительная часть светового потока локализована за пределами требуемой прямоугольной области.

В ряде случаев задача поиска интегрируемого лучевого отображения может быть сведена к задаче Монжа–Канторовича о перемещении масс (ЗПМ) со специальной функцией стоимости [27–29]. Решение ЗПМ в общем случае требует использования специализированных вычислительных алгоритмов и обладает большой вычислительной сложностью.

В настоящей работе предложен новый вид лучевого отображения в задаче расчёта преломляющих оптических элементов для формирования заданных двумерных распределений интенсивности. Отметим, что в данной задаче считается выполненным условие дальней зоны, которое означает, что размерами оптического элемента можно пренебречь по сравнению с расстоянием до освещаемой плоскости. В этом случае преломляющий элемент рассматривается как точечный источник, закон излучения которого описывается функцией интенсивности.

Предложенное в работе отображение является обобщением лучевого отображения из задачи расчёта преломляющей поверхности для формирования однопараметрического распределения интенсивности в виде «отрезка», для которой получено аналитическое решение [21]. В [21] показано, что лучи, направляемые преломляющей поверхностью в каждую точку отрезка, находятся на поверхности кругового конуса с вершиной в источнике излучения. В данной работе предлагается использовать данный тип лучевого отображения при формировании двумерных распре- делений интенсивности, соответствующих «полосе». Под полосой понимается вытянутая область, получаемая из исходного отрезка заменой каждой точки на отрезок, перпендикулярный исходному (рис. 1). В рамках предложенного в работе лучевого отображения расчет оптического элемента сводится к решению обыкновенных дифференциальных уравнений 1-го порядка, разрешенных относительно производной. Нужно отметить, что хотя предложенное лучевое отображение в общем случае не является интегрируемым, представленные результаты расчета показывают хорошие рабочие характеристики предложенного метода. При формировании прямоугольных распределений интенсивности с угловыми размерами от 80°×1° до 40°×20° относительная среднеквадратичная ошибка формирования заданной постоянной интенсивности не превысила 15 %.

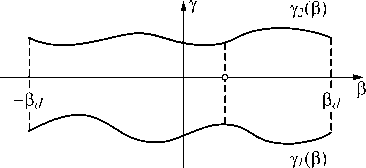
Рис. 1. Геометрия двумерной освещаемой области (полосы)

• 1. Расчет преломляющей поверхности для формирования распределения интенсивности в виде отрезка

Рассматриваемый в работе метод расчета преломляющих оптических элементов для формирования заданных двумерных распределений интенсивности основан на методе расчета преломляющей поверхности для формирования однопараметрического распределения интенсивности. В этой связи сначала рассмотрим задачу формирования однопараметрического распределения интенсивности в виде отрезка. Аналитическое решение данной задачи было получено в работе [21]. Однако для полноты изложения и введения основных понятий кратко повторим основные результаты работы [21].

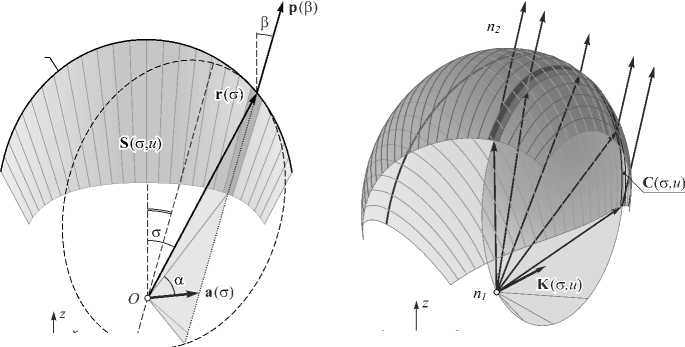
Пусть в начале координат в среде с показателем преломления n 1 > 1 расположен точечный источник излучения с функцией интенсивности I 0 ( σ , u ), где ( σ , u ) – некоторые криволинейные координаты, задающие направления исходящих из источника лучей. Над источником расположена преломляющая поверхность S ( σ , u )=( x ( σ , u ), y ( σ , u ), z ( σ , u )), разделяющая среду с показателем преломления n 1 и среду с показателем преломления n 2 = 1 (рис. 2 а ). Задача состоит в расчёте поверхности S ( σ , u ) из условия формирования заданного однопараметрического распределения интенсивности I ( β ), где β ∈ [ – β d , β d ] – угловая координата, задающая направления преломленных на поверхности лучей.

В рассматриваемом случае координата в соответствует углу между проекцией преломленного луча на плоскость x O z и осью z . При этом направления преломленных на поверхности S ( а , и ) лучей задаются следующей вектор-функцией (рис. 2 а ):

Р ( в ) = ( sin в , 0, cos в ) , ве [ —в d , в d ] .                (1)

Поскольку функция p ( в ) описывает направление на точки отрезка в дальней зоне, то далее мы будем называть её отрезком.

S(a.O)

а)

С (ст,;/)

б)

в)

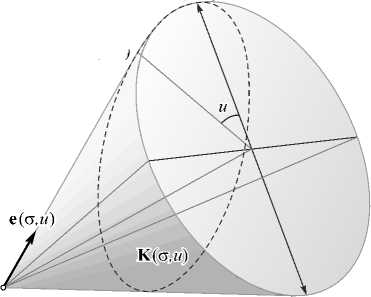
Рис. 2. Геометрия задачи расчёта преломляющей поверхности для формирования однопараметрического распределения интенсивности в виде отрезка: проекция на плоскость xOz (а); изометрическая проекция и схематическое изображение конуса лучей (б); геометрия кругового конуса K(a, и) (в)

Без ограничения общности будем считать, что при и = 0 координатная линия S ( а , 0) = ( x ( а , 0), 0, z ( а , 0)) соответствует центральному сечению поверхности S ( а , и ) плоскостью у = 0. В качестве координаты а будем использовать угол между направлением на точку центрального сечения S ( а , 0) и осью z (рис. 2 а ). Пусть r = r ( а ) - модуль радиус-вектора центрального сечения, а в = в ( а ) - функция, задающая направления преломленных лучей на профиле S ( а , 0) (рис. 2 а ). Функции r ( а ) и в ( а ) связаны законом Снеллиуса, который в дифференциальной форме может быть представлен в виде [21]:

dr (а) = - r (а)    ып(а-в(а))

d а          1/ n ₂₁ - cos( а-в ( а ))

где n21 = n2 / n1. В работе [21] показано, что поверхность S (а, и) можно представить в виде огибающей однопараметрического семейства эллипсоидов по параметру а с первым фокусом в начале координат (в точке расположения точечного источника) и направлением большой оси p (а) = p (в(а)). Каждый эллипсоид семейства преобразует сферический пучок от источника в пучок с плоским волновым фронтом и направлением p (а). Уравнение огибающей поверхности имеет вид [21]:

8 ( а , и ) = е ( а , и ) ■ l ( а , и ) = е ( а , и ) ■

У ^{( а )} 1 - n 21 ( е ( а , и ), p ( а ) )

, (3)

где l ( а , и ) - расстояние от источника излучения до точки эллипсоида по направлению e ( а , и ), где координата и единичного вектора e ( а , и ) будет объяснена ниже. Значения ^ ( а ) и n ₂₁ в (3) имеют смысл фокальных параметров и эксцентриситета эллипсоидов семейства, формирующих огибающую поверхность.

В качестве иллюстрации на рис. 2 а показан один из эллипсов, касающийся центрального сечения огибающей поверхности в точке S ( а , 0). Данный эллипс является сечением плоскости y =0 соответствующего эллипсоида, преобразующего сферический пучок от источника в пучок с направлением p ( а ) . Функция ^ ( а ) в (3) может быть выражена через функции r ( а ) и в ( а ) в виде [21]:

^(а) = r (а)^(1 - n 21 cos (а-в(а))). (4)

В работе показано [21], что падающие от источника лучи, которые после преломления на поверхности S ( g , u ) имеют направление pi ( g ) = p ( P ( g ) ) , лежат на поверхности кругового конуса K ( g , u ) с вершиной в начале координат (рис. 2 б ). Образующие конуса соответствуют отрезкам, соединяющим начало координат с точками пересечения эллипса и прямой с направляющим вектором p ( g ) , проходящей через точку касания эллипса и центрального сечения (рис. 2 а ). Сечения данных конусов плоскостями

- ( x - x ( g , 0)) cos P ( g ) + ( z - z ( g , 0)) sin P ( g ) = 0 (5)

образуют преломляющую поверхность [21]. Одно из сечений C ( g , u ) показано пунктирной линией на рис. 2 б . Отметим, что указанные сечения также принадлежат эллипсоидам, образующим огибающую поверхность (2) [21]. Поэтому в качестве вектора e ( g , u ) в (2) можно использовать единичный вектор образующей соответствующего конуса K ( g , u ). В качестве координаты u при задании вектора e ( g , u ) и, соответственно, преломляющей поверхности S ( g , u ) будем использовать угол, определяющий положение точки в сечении конуса плоскостью, перпендикулярной оси конуса (рис. 2 в ). В этом случае, как предполагалось выше, при u = 0 S ( g , u ) определяет центральное сечение поверхности S ( g , u ). Отметим, что пунктирная линия на поверхности конуса на рис. 2 в соответствует сечению C ( g , u ) преломляющей поверхности, показанному на рис. 2 б .

Из геометрии задачи вектор e ( g , u ) может быть получен в виде [21]:

где

a ( G ) = arccos

sin ( g-P ( g ) )

1 - 2 n ₂₁ cos ( g-P ( g ) ) + n ₂₁ ²

угол при вершине конуса, t ( g ) = a ( G ) + g . Отметим, что функции a ( G ) и t ( g ), определяющие компоненты вектора e ( g , u ), выражаются через функцию P ( g ).

Из формул (3) – (7) можно видеть, что преломляющая поверхность S ( g , u ), формирующая отрезок p ( g ) = p ( P ( g ) ) , функционально зависит от функции Р = P ( g ). Данная функция рассчитывается из закона сохранения светового потока из условия формирования заданного распределения интенсивности I ( Р ), Ре[ Р d , Р d ] [21]. Из (3), (6) можно получить элемент телесного угла, соответствующий элементу поверхности S ( g , u ), в следующем виде [21]:

d Q c

de (g, u) 5g

de (g, u) du

• / \ (da(G) sin a(G) ——^- v ( 5g

dadu =

5t ( g ) )

cos u —-—- dGd u .

5g I

Соответственно, закон сохранения светового потока может быть записан виде [21]:

I ( Р ) d p® d g

	- sin a ( a ) cos t ( g ) cos u +^ + cos a ( a )sin t ( g ),
e ( u , g ) =	sin u sin a ( a ), sin a ( a ) sin t ( g ) cos u + ^ + cos a ( a )cos t ( g )     ^	,                 (6)

где

R ( g , P ( g ) ) =

c                , । Sa(G)         6t(g)|

1 ₀( u , G )sin a l G )-- cos u------ du .

²                / 5g          5g J

Из (9) для расчета функции P ( g ) может быть получено следующее обыкновенное дифференциальное уравнение [21]:

d P ( g ) =      F2 ( g , u ) - R ( g , P ( g ) ) ^[ F i ( g , u ) - F 2 ( g , u ) ]

dG    I (P(g))/sin a(G) - R (g, P(g) )[ F (u, g)- F (u, a)]’

n 21 cos ( g-P ( g ) ) - 1

n 21 - 2 n ₂₁ cos ( g-P ( g ) ) + 1

F ( g , u ) = | 0 ^S ( ’ в ) 1 ₀ ( g , u ) d u ,

F2 (g, u) =

r g ( ^G’ P )

J0

1 ₀ ( g , u ) cos u d u .

Верхний предел интегрирования g ( g , в ) в выражениях (12) и (13) есть некоторая функция, определяющая размер преломляющей поверхности по переменной u при фиксированном значении g [21].

Таким образом, расчет преломляющей поверхности для формирования однопараметрического распределения интенсивности в виде отрезка сводится к выполнению следующих шагов:

• 1.    Расчет функции P ( g ) из решения дифференциального уравнения (10).

• 2.    Расчет функции r ( g ) из решения дифференциального уравнения (2).

• 3.    Расчет функции ^ ( g ) по формуле (4).

• 4.    Расчет преломляющей поверхности S ( g , u ) по формулам (3), (4), (6), (7).

2. Расчет преломляющей поверхности для формирования двумерного распределения интенсивности

Рассмотрим далее задачу формирования заданного двумерного распределения интенсивности I ( Р , y ),( P , у ) € D , где

D = [-Рd, Рd ] x [Y1 (Р), Y2 (Р)] Va2 + b2 .

В данном случае у - угол, отсчитываемый от плоскости xOz, а функции у ₁( в ), у ₂( в ) определяют границы освещаемой области D по переменной у (рис. 1). Угол в , как и в параграфе 1, соответствует углу между проекцией преломленного луча на плоскость xOz и осью z. В частном случае y i ( P ) = у ₂( в ) = 0 область D соответствует отрезку (1). При формировании двумерного распределения интенсивности направления преломленных поверхностью лучей имеют вид:

Р ( в , Y ) = ( sin Р cos Y , sin Y , cos в cos y ) ■ (14)

Рассмотрим задание лучевого отображения P = P(a, и), Y = Y(a, u), определяющего координаты преломленных лучей через координаты падающих от источника лучей, в задаче формирования двумерного распределения интенсивности I(в,у). В задаче формирования однопараметрического распределения интенсивности конусы лучей K (а, и) отображались в точки p (а) = p (3(c)) отрезка (1) (рис. 2б). При формировании двумерного распределения интенсивности предлагается использовать обобщение этого отображения. Определим функции в = в(а, и) и у = Y(a, и) из условия, что конусы лучей, задаваемые вектором e(a, и) в (6) при фиксированных значениях а, преобразуются преломляющей поверхностью в «отрезки» p(P(a), у), уе[у1(Р(а)), у2(в(а))], являющиеся поперечными сечениями заданного двумерного распределения интенсивности. В этом случае функцию Р(а, и) = Р(а) предлагается рассчитывать из условия формирования однопараметрического распределения интенсивности. Поскольку элемент телесного угла, соответствующего вектор-функции (14), имеет вид dQ = cos у dpdy, то указанное однопараметрическое распределение интенсивности получается интегрированием по Y заданного двумерного распределения с весом cos у:

• Y 2 ( Р )

I(Р)= J I(Р,у)cosYdy,pe[-pd,вd]■           (15)

• Y 1 ( P )

Расчет функции P ( a ) осуществляется на основе интегрирования дифференциального уравнения (10).

Для расчета функции у = Y ( а , и ) воспользуемся законом сохранения светового потока:

I ( Р , y ) cos Y d p d y = I о ( а , и ) d Q _c ,                 (16)

где 10(a, и) — интенсивность источника излучения, а dQc — элемент телесного угла (8), соответствующего вектор-функции e (а, и). Подставляя (8) в (16), получим для функции y = Y (а, и) обыкновенное дифференциальное уравнение dy(a,и) 10(а,и)sinа(а)(dа(а)/dа-cos(и) dт(а)[dа) dи                    I(Р, y)cos y dp/da

где d p /d a имеет вид (10), углы конусов а ( а ) определены уравнением (7), а т ( а ) = а ( а ) + а . Отметим, дифференциальное уравнение (17) определяет функцию у ( а , и ) при каждом фиксированном значении а .

Рассмотрим теперь восстановление преломляющей поверхности, используя рассчитанные функции Р ( а ) и у ( а , и ). Определим преломляющую поверхность S ( а , и; Р , у ), формирующую двумерное распределение интенсивности I ( в , у ), ( в , Y ) ^e D , в виде огибающей двухпараметрического семейства эллипсоидов по параметрам ( в , у ) е D [27-29].

Каждый эллипсоид семейства преобразует сферический пучок от источника в пучок с плоским волновым фронтом и направлением p ( P , у ). Уравнение огибающей поверхности определяется уравнением эллипсоида

S ( а , и ; Р , y ) = e ( a , и ) ■ l ( а , и ; в , у ) =

= ( ) v(e, y)

, 1 - n 21 ( e ( a , и ), p ( P , y ) )

и условием равенства нулю частных производных функции l ( a , и; p , у ) по параметрам ( p , у ) [21]:

d l ( a , и ; P , y ) = о d l ( a , и ; P , y ) = о dp ’ dY

Выражения (19) можно представить в виде:

d In y(3, y) =- n 21 (e(a, и), dp(P, y)/dP) dP           1 - n21 (e(a,и),p(P, y)) ’ d In v(P, Y) = n 21 (e(a, и), dp(P, y)/ду) dy           1 - n 21 (e(a, и), p(P, y) )

Для расчета преломляющей поверхности необходимо вычислить функцию ^ ( P , у ), представляющую фокальные параметры эллипсоидов (18). Действительно, при известной функции ^ф, у ) преломляющая поверхность рассчитывается по формуле

С / А A    V(p(a), Y(a,иЙ

^{S (a} , ^и ) = ^{e (a} , ^и )------—---—----,        ⁽²¹⁾

1 - n ₂₁ ( e ( a , и ) , p ( a , и ) )

где p(a,и) = p(p(a),y(a,и)). Для расчета функции ^(Р, у) предлагается следующий метод. Введем функцию G (Р, y) = ln V(P, Y) и аппроксимируем её двумерными B-сплайнами [40]. Область D, на которой определена функция G (Р, у), а также заданное распределение интенсивности I(Р, у), ограничена прямоугольником с размерами сторон 2р d и 2у d, где уd = maxЦу1 (р}|,|у2 (р}|] . Зададим на отрезке [-вd, вd] набор из M эквидистантных узлов. Используя данные узлы, введём B-сплайны порядка q и обозначим их как Bm (Р), m = 1,..., M + q -2 [40]. Аналогичным образом введём B-сплайны Pn(у) по второй координате уе[-уd, уd]. Представим теперь функцию G (Р, у) в виде разложения по введённым базисным функциям:

G (в, У) = £ PmnBm (в) Pn (у), (22) m,n где pmn – коэффициенты разложения. Отметим, что в случае, когда сплайны Bm(в) и Pn(у) имеют один порядок и одинаковое число узлов, представление (22) содержит N =(N1 + q –2)2 неизвестных коэффициентов pmn.

Будем считать, что функции в ( а ) и у ( а , и ), получаемые из решения дифференциальных уравнений (10) и (17), заданы в дискретном наборе точек ( а i , u i ), i = 1,..., N . Тогда коэффициенты p_mn предлагается определить из условия, что частные производные д G / дв , д G / дУ сплайна (22) в точках ( в ' , У ' ) = ( в ( а i ), У ( а i , U i )), i = 1,..., N являются аппроксимацией по методу наименьших квадратов производных (20), рассчитанных в точках ( в i , У i ) и ( а i , u i ), i = 1,..., N . Таким образом, расчет коэффициентов p_mm сводится к решению следующей задачи минимизации:

е(p) = Z ^F(P',У-,а,u')"^'’У') + д In v

—— (в ' , У ' , а ' , и ) -дУ

+ Z

д Gzr .

—(Pi, У')  ^ min,

ду J

где p — вектор коэффициентов сплайна. Несложно показать, что решение задачи (23) сводится к стандартному методу наименьших квадратов. Данный подход, состоящий в аппроксимации производных оптической поверхности, позволяет скомпенсировать ошибки, возникшие при расчете лучевого отображения [27, 29].

Таким образом, расчет преломляющей поверхности для формирования двумерного распределения интенсивности сводится к выполнению следующих шагов:

• 1.    Расчет требуемого однопараметрического распределения интенсивности / ( в ) по формуле (15).

• 2.    Расчет функции в ( а ) из решения дифференциального уравнения (10).

• 3.    Расчет функции у ( а , и ) из решения дифференциального уравнения (17).

• 4.    Восстановление функции G ( в , у ) = 1п v ( в , У ) из ее частных производных (20), используя описанный выше метод.

• 5.    Расчет преломляющей поверхности S ( а , и ) по формулам (6), (14), (21).

3. Примеры расчета

При проектировании преломляющих оптических элементов необходимо учитывать френелевские потери (т.е. потери, связанные с частичным отражением света от преломляющей поверхности) и возможность полного внутреннего отражения световых лучей от поверхности оптического элемента. Для уменьшения френелевских потерь в данной работе предлагается дополнительно использовать внутреннюю осесимметричную поверхность (рис. 3). Эта преломляющая поверхность формирует мнимый источник излучения, смещённый вниз по оси Oz. При этом уменьшаются углы падения лучей на внешнюю поверхность, формирующую заданное распределение интенсивности, и, соответственно, снижаются френелевские потери и вероятность полного внутреннего отражения. Профиль внутренней поверхности определяется уравнением картезианского овала [24].

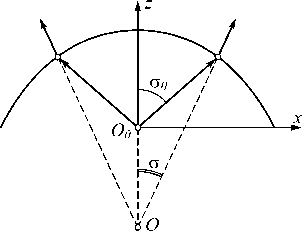
Рис. 3. Профиль преломляющей поверхности, формирующей мнимый источник, смещённый по оси z.

Определяется уравнением картезианского овала

С использованием описанного в работе метода построения лучевого отображения были рассчитаны преломляющие оптические элементы для формирования постоянной интенсивности света в прямоугольных областях в диапазоне угловых размеров от 80°×1° до 40°×20° (табл. 1). Расчет производился для точечного ламбертовского источника излучения.

Табл. 1. Примеры расчёта оптических элементов и результаты их моделирования с размерным источником излучения со стороной 1,5 мм

№ примера	Размер освещаемой области, град	Длина, ширина и высота оптического элемента, мм	Световая эффективность, %	СКО
1	80×1	43,6×27,0×28,3	82,13	3,62
2	80×20	38,6×28,6×31,3	83,78	10,6
3	60×20	36,9×28,9×28,3	80,36	13,4
4	40×20	32,3 × 28,9 × 28,37	75	15

Во всех примерах лучевые отображения с шагом в 1° были найдены из решений обыкновенных дифференциальных уравнений (10) и (17). Внешние пре- ломляющие поверхности были рассчитаны по формулам (6), (14) и (21) через полученное лучевое отображение. Для определения функции v(P, У) в формуле

• (21) функция G ( β , γ )=ln ψ ( β , γ ) была восстановлена двумерными B-сплайнами 3-го порядка из её частных производных (20), используя 2048 узловых точек. Подробное описание этапов расчета приведено в конце предыдущего параграфа. Внутренняя поверхность была рассчитана из условия формирования мнимого точечного источника излучения, смещенного относи-

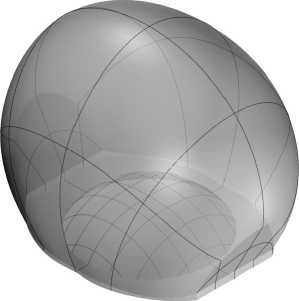
• тельно начала координат по оси Oz на Δz =–2, 0. Такое значение смещения было выбрано эмпирически, на основании анализа потерь Френеля. Высота внутренней поверхности составила 4,5 мм. В связи с тем, что внешние преломляющие поверхности очень похожи, на рис. 4 изображены только три оптических элемента – для примеров 1, 3, 4 из табл. 1.

Рис. 4. Преломляющие оптические элементы для формирования постоянной интенсивности света в прямоугольной

б)

в)

области с угловыми размерами: (а) 80×1 (пример 1 в табл. 1), (б) 60×20 (пример 3 в табл. 1), (в) 40×20 (пример 4 в табл. 1)

В силу симметрии формируемого распределения интенсивности рассчитываемые оптические элементы симметричны относительно плоскостей x O z и y O z . В связи с этим расчёт преломляющих поверхностей производился для ϕ ∈ [0, π /2], где ϕ – азимутальный угол сферической системы координат. При этом «полные» поверхности оптического элемента (при ϕ ∈ [0, 2 π ]) получаются из поверхностей при ϕ ∈ [0, π /2] последовательным отражением относительно плоскостей симметрии ϕ = π /2 и ϕ =0.

Отметим, что поскольку в рассматриваемой задаче выполняется условие дальней зоны, то преломляющие поверхности могут быть отмасштабированы относительно начала координат для получения оптического элемента нужных габаритов. Такое масштабирование никак не повлияет на результаты моделирования работы элемента.

Для иллюстрации на рис. 5 приведено лучевое отображение, рассчитанное предложенным методом для задачи формирования равномерного распределения интенсивности в прямоугольной области с размерами 60° × 20°. В левой части рисунка изображена стереографическая проекция единичной сферы, на которой определена функция интенсивности источника излучения, из точки (0; 0;–1) на плоскость z=0 [37]. Справа на рис. 5 изображена область определения требуемого распределения интенсивности в координатах β и γ .

Было проведено моделирование работы рассчитанных оптических элементов методом трассировки лучей в коммерческом программном обеспечении TracePro [41]. Для реалистичности в качестве источника излучения использовался ламбертовский источник излучения с размером 1,5×1,5 мм2. На рис. 6 представлены распределения интенсивности, рассчи- танные методом трассировки лучей при числе лучей N =500000.

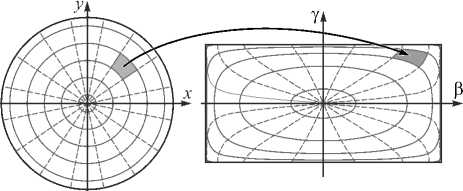
Рис. 5. Структура лучевого отображения для преломляющего оптического элемента, формирующего постоянную интенсивность в прямоугольной области размером 60°×20°

Для оценки качества формируемого светового распределения использовались среднеквадратичное отклонение (СКО) формируемого распределения интенсивности от равномерного в заданной области и световая эффективность, равная доле излученного источником светового потока, попавшей в эту область. В табл. 1 приведено краткое описание примеров – размеры освещаемой области, размеры рассчитанного оптического элемента и результаты моделирования.

Отметим, что представленный метод предназначен для освещения областей с малым поперечным размером (с большим аспектным соотношением). Несмотря на это, СКО не превосходит 15 % даже для прямоугольной области с угловыми размерами 40°×20° (табл. 1).

Представленные примеры демонстрируют высокую эффективность предложенного метода в задачах расчёта преломляющих оптических элементов для формирования двумерных распределений интенсивности прямоугольной формы.

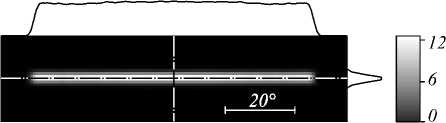
б)

Рис. 6. Распределения интенсивности, рассчитанные в программе TracePro, формируемые преломляющими оптическими элементами при протяженном источнике излучения со стороной 1,5 мм.

Размеры требуемых областей: 80°×1° (а), 80°×20° (б), 60°×20° (в), 40°×20° (г)

г)

Заключение

Предложен новый вид лучевого отображения в задаче расчёта преломляющих оптических элементов для формирования заданных двумерных распределений интенсивности. В рамках предложенного в работе лучевого отображения расчет оптического элементы сводится к решению обыкновенных дифференциальных уравнений 1-го порядка, разрешенных относительно производной. Представленные результаты расчета показывают хорошие рабочие характеристики предложенного метода. При формировании прямоугольных и эллиптических распределений интенсивности с угловыми размерами от 80°×1° до 40°×20° относительная среднеквадратичная ошибка формирования заданной постоянной интенсивности не превышает 15 %.

Полученные в работе теоретические результаты расширяют класс методов, которые могут быть использованы для расчёта начальных приближений в оптимизационных методах расчёта преломляющих оптических элементов.

Работа выполнена при поддержке Российского научного фонда (проект №18-19-00326).